近鄰問題的亞線性算法研究現狀綜述

馬恒釗，李建中，2

（1 哈爾濱工業大學 海量數據計算研究中心，哈爾濱 150001；2 中科院深圳理工大學，廣東 深圳 518107）

0 引言

近年來，大數據概念已經在研究界和應用界越來越熱門，這也表明大數據時代已然來臨。許多應用已經開始日常處理起TB 級數據，比如廣為人知的TeraSort 應用。而在一些場景、比如科學數據中，甚至開始面對PB、以及EB 級數據，諸如大型綜合巡天望遠鏡（Large Synoptic Survey Telescope，LSST）每天生成的數據量就達到1.25 PB。下面做一個簡單的計算。設想要通過SSD 固態硬盤來讀取數據，目前SSD 的最大讀帶寬約為6 GB/s，于是，僅讀取1 PB 數據就需要34.7 h，讀取1 EB 數據甚至需要超過4 年時間。這表明，在處理大數據時，串行線性算法的運行時間也有可能是不可接受的。如何高效地處理這樣天文級數量的數據，成為理論研究界和應用界共同的挑戰。應用界提出的解決辦法一般是并行化，比如淘寶應對雙十一的海量事務處理請求所用的就是阿里云等并行處理平臺。但是從理論界看來，并行化有以下一些問題：

（1）有些問題是無法高效并行化的。

（2）并行化并不能降低問題的復雜度。

（3）并行化帶來了通信復雜度和通信瓶頸等問題。

（4）這也是最重要的一項，并行化有可擴展性和加速比的問題，即當所使用的處理器數量達到一定閾值時，再增加處理器將無法降低總運行時間，甚至還有可能會增加總運行時間。因此，理論界解決大數據問題所提出的方案是設計亞線性算法，即時間復雜度為（logn）或者（n）的算法，其中0，1。只有設計亞線性算法，才能從根本上降低算法的時間復雜度，減小處理大數據所需要的時間。

根據文獻［5］提出的理論，亞線性算法分為2類。其一為純亞線性算法，即可以直接通過亞線性算法解決的問題；其二為偽亞線性算法，即經過一個多項式時間的預處理后，再通過亞線性算法可以解決的問題。前者包括判定數組是否為ε-far 單調問題，具體算法參見文獻［6］。后者則包括眾所周知的無序數組查找問題，即在無序數組上查找元素，可以通過花費（）時間進行排序，再通過（1）時間的二分查找予以解決。亞線性算法已經有接近二十年的研究歷史，最初的研究內容集中于屬性測試，后來又拓展至圖算法、計算幾何、代數計算等領域。參見綜述文獻［11］。這些問題在許多領域都有廣泛的應用，比如生物信息、物聯網、軌跡分析、機器學習、推薦系統等。然而對于近似最近鄰領域，其亞線性算法的研究卻還未臻充分。本文對該問題的亞線性算法的研究現狀做了綜述。

1 全k-最近鄰問題算法概述

全k-最近鄰問題簡記作All-kNN。關于此問題的工作最早可以追溯到1983 年，且近年來也一直有關于此問題的研究工作出現。此問題備受各方關注的原因，是因為許多應用都以AllkNN 問題作為重要的子程序，比如分類、凝聚式聚類、圖像檢索、推薦系統以及離群點檢測等。在許多類似的應用中，計算All-kNN 都是主要的瓶頸。

由于該問題的重要性，歷史上研究者們提出了許多算法試圖高效地解決All-kNN 問題，這些算法可以分為以下3 類：

（1）第一類算法。使用各種不同的技巧來降低算法的實際運行時間，然而這些算法的最壞時間復雜度仍為（）不變。據研究分析可知，這些算法大致有3 種算法設計技巧。分述如下。

①第一種，基于樹型的空間索引。如樹和Voronoi 圖等。

②第二種，基于空間填充曲線，包括希爾伯特曲線和Z-order 曲線等。空間填充曲線是一類在高維數據上建立一維索引的方法，基于空間填充曲線構建的索引具有一種重要特性，即在空間上相近的點更容易被分配到相近的索引項中。據文獻［19，29-30］中的結果，此性質有助于降低計算All-kNN時需要計算距離的次數。

③第三種，基于近鄰傳播的思想，即近鄰的近鄰仍很有可能是近鄰。NN-descent 算法是提出此思想的開創性工作，且仍是目前All-kNN 問題最好的算法之一。其他使用此思想的算法一般先以某種方法作為預處理，再使用近鄰傳播技巧來提高結果的精度。例如，文獻［32］中使用隨機分治方法作為預處理，而文獻［33］中使用局部敏感哈希方法作為預處理。

（2）第二類算法。是在并行環境下解決問題。文獻［34］理論上證明了All-kNN 問題存在并行最優算法，該算法在CREW PRAM 模型上需要（）時間和（）個處理器。其他工作則致力于在不同的并行平臺上解決All-kNN 問題，比如MapReduce 平臺和GPU 環境。

上述算法的最壞時間復雜度上界都為（），第三類算法則不同，現已都被證明了具有更低的時間復雜度，且都是串行算法，與文獻［34］中給出的并行算法也不同。例如，Bentley給出了一種多維分治算法，可以在（（1））時間內解決AllkNN 問題，其中是數據的維數。又如，文獻［17］中給出的算法需要（（））時間，其中是輸入數據點集中最遠的一對點和最近的一對點的距離之比。再者，文獻［39］中給出的算法聲明具有（kdnlogn）的時間復雜度上界。最后，研究發現了文獻［39］中算法的一個錯誤，在文獻［40］中給出了嚴格的證明，證明文獻［39］中的算法的下界為（），并提出了新的算法，真正具有（）時間上界。

2 近似最近鄰問題算法概述

近似最近鄰問題，簡記作ε-NN，是一個在理論研究和應用研究方面都很重要、且基礎性的問題，自19 世紀90 年代起就有許多相關的解決算法被提出，這些算法可以分為4 類，如下所述。

（1）第一類算法，試圖直接解決問題，且這些算法一般都設計了預處理數據結構來支持算法的高效運行。Arya 等人研究提出了一種算法，需要1/ε·空間，1/ε·預處理時間以及1/ε·查詢時間。另有研究提出的算法需要（）空 間、（）預處理時間和（/）·查詢時間。Kleinberg 在文獻［14］中提出了2 個算法。其一是確定性算法且達到了（（））查詢時間，使用的數據結構需要（（））空間和（（））預處理時間；其二是隨機化算法，預處理時間為（·），所需的空間降至為（·）但其查詢時間卻提升為（·）。

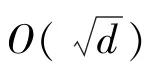
（3）第三類算法，試圖從另一個角度考慮ε-NN問題。算法利用了數據的一種內生維度，而非原始數據所存在的歐氏空間的維度。文獻［17］給出了一個代表性的工作，該文獻中提出的算法的查詢時間復雜度上界為2（1），其中（）為輸入點集的內生維度，是的直徑。

在上述3 類算法之外，Indyk 等人開創了第四類算法。這類算法的關鍵思想在于定義了一個近似近鄰問題，記作（，）-NN，然后將-NN 問題歸約到此問題。于是解決-NN 問題的過程就分為了2 部分，一是解決（，）-NN 問題，二是設計從-NN 到（，）-NN 的歸約。目前，有3 個現存工作設計了從-NN 到（，）-NN 的歸約算法。對此擬做闡釋分析如下。

（1）第一個歸約算法是文獻［18］中提出的，所構造的數據結構需要（·（））空間，其查詢時間為（）。

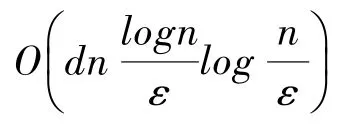
（3）第三個算法在預處理階段調用（，）-NN 算法來構造數據結構，其查詢時間為（log），此處的指數（1）來自于算法的常數成功概率的要求。這3 個現存算法的查詢時間都是比較高的，目前已在文獻［41］中提出了新的圖靈歸約算法，具體查詢時間為（1），低于所有上述現存算法。

3 近似k-最近鄰問題算法概述

近似k-最近鄰問題，簡記作kANN 問題，是近似最近鄰問題的自然推廣，已在許多應用領域都有重要應用，比如數據可用性、數據庫查詢、以及圖算法等。對于kANN 問題有2 種近似標準，分別稱作距離標準和召回率標準。其中，距離標準要求近似結果集中的點到查詢點的最遠距離和精確結果集中的點到查詢點的最遠距離之比不超過給定閾值。召回率標準要求近似結果集和精確結果集的交集大小不小于給定閾值。下面將簡要討論現存工作是如何考慮上述2 個近似標準的。

關于kANN 問題的現存算法可以分為4 類。這里給出探討剖析如下。

（1）第一類算法，是基于樹的方法。這種方法的主要思想是將度量空間遞歸地劃分為子空間，并組織成樹結構。K-D 樹是這種思想的代表性工作，但是這種方法只在低維空間中有效，當維度數升高時其性能會大幅下降。Vantage point 樹是另一種基于樹的方法，在方法性能上對K-D 樹有所提升。FLANN 方法是最近的工作且在高維空間中有更好的表現，但是卻有可能輸出非最優的結果。據研究所知，現存的基于樹的方法對距離標準和近似標準都沒有理論保證。

（2）第二類算法，是基于置換的方法。方法的思想是挑選一個樞軸點的集合，并將每個數據元素表示成這些樞軸點的一個置換，這個置換是通過將樞軸點按照和數據元素的距離排序來得到的。在這種表示方法中，距離較近的數據元素的置換表示也相似。利用這種思想的方法包括MI-File和PPIndex。然而，據分析可知，這些方法也沒能給出對距離標準和召回率標準的理論保證。

（3）第三類算法，是基于局部敏感哈希（Locality Sensitive Hashing，LSH）的方法。LSH 最初由Indyk等人提出，并應用于解決1 時的kANN 問題。不久之后，Datar 等人提出了第一個實用的LSH函數，此后關于LSH 的理論和應用研究就大量出現。例如，Andoni 等人證明了基于LSH 的算法的最優時空下界，并提出了符合下界的最優的LSH 函數。在應用方面，Gao 等人提出了一種致力于彌合LSH 的理論和kANN 應用的算法。可以參考概述文獻［59］。基本的LSH 算法只能在1 的情況下滿足距離標準。一些較晚近的算法有更多的進展。比如C2LSH解決了距離標準下的kANN 問題，但是卻要求近似因子必須是整數的平方。SRS 算法也是針對距離標準下kANN 問題的算法，但是卻只有部分的理論保證，即只有算法在特定條件下結束時，返回的結果才能滿足距離標準。

（4）第四類算法，是基于圖的算法。在這類算法中用到的特殊的圖稱為近似圖，其中的邊是基于頂點之間的幾何關系定義的。可以參考概述文獻［63］。例如，Paredes 等人使用了kNN 圖，Ocsa等人使用的是相對鄰居圖（Relative Neighborhood Graph，RNG），Malkov 等人使用的是可導航的小世界圖（Navigable Small World Graph，NSW）。在這種基于圖的kANN 算法中經常用到在近似圖上的導航過程，即選擇圖上的某一個頂點作為起始點，并按照某種特定的導航策略來向著目標頂點移動。據分析可知這種上述的這些方法都無法在理論上滿足距離標準和召回率標準。

總之，大部分現存算法在距離標準和召回率標準上都沒有理論近似保證。在現存工作中，召回率標準只被用于度量實驗結果的好壞程度，距離標準則只被少數算法部分地滿足。故在文獻［67］中提出了將2 個近似標準結合起來的新問題，并提出了針對該問題的算法，通過理論分析，證明了在輸入服從泊松點過和的情況下，算法返回的結果能夠至少滿足其中一個近似標準，并證明了算法的期望預處理時間復雜度為（），期望空間復雜度為（），期望查詢時間復雜度為（1）。

4 結束語

在本文中，研究回顧了近鄰問題中的全k-最近鄰問題、近似最近鄰問題及近似k-最近鄰問題，主要介紹了這些問題現有算法的時間復雜度。從中可以看出，這些問題的現有算法的時間復雜度都無法達到亞線性，因此在可接受的時間內將無法在PB級大數據上求得計算結果。研究者應該更多關注于亞線性時間算法的設計與分析，從而能夠應對大數據時代的高效計算需求。