基于自運動的冗余機械臂實時避障軌跡規劃

高其遠，陳 麗

（上海工程技術大學 航空運輸學院，上海 201620）

0 引言

冗余機械臂的關節自由度高，工作范圍大，能夠應對多種工作環境，完成復雜任務。在實際工作中，需要根據機械臂的工作任務，規劃運動軌跡，并滿足避障需求。

現有研究中，針對機械臂的軌跡規劃算法主要有人工勢場法、隨機搜索法。其中，人工勢場法由Khatib提出，通過在目標與機械臂之間引入吸引力，在障礙物與機械臂之間引入排斥力，從而實現機械臂的避障軌跡規劃。人工勢場法在計算時容易陷入局部極小值，難以適應復雜環境。Laliberte 等人針對人工勢場法容易發生局部極小的不足，提出了離散勢場法，從而降低了發生局部極小的可能性。隨機搜索法通過在機械臂關節空間內任意搜索機械臂運動路徑點，適合復雜環境下的路徑搜索。Lozano-Perze提出的一種基于空間法的自由空間法，先根據機械臂的各個關節約束范圍建立機械臂所有可行空間，再將障礙物映射到空間內，進而求解空間內除去障礙物的補集空間，即機械臂不會發生碰撞的自由空間。賈慶軒等人引用A算法在冗余機械臂的空間內進行搜索，獲得無碰撞路徑。隨機搜索法在機械臂自由度高時，機械臂自由運動的空間構建困難，難以滿足實時性需求。基于隨機采樣的路徑搜索算法在機械臂的關節空間進行搜索，不必求解高維空間，代表算法有快速擴展隨機樹法（Rapidly-exploring Random Trees，RRT）、隨機路圖法（Probabilistic roadmaps，PRM），由于是隨機采樣生成路徑點，在復雜環境下可能無法搜索出無碰撞路徑，且難以控制過程中末端執行器位姿，也難于滿足需要約束機械臂抓取姿態的任務要求。

冗余機械臂具有自運動的特性，相同的末端姿態可對應多組關節角度，故可利用該特性避障。姜力等人通過引入臂平面和避障面表達機械臂的零空間自運動。齊志剛等人根據臂型角參數化完善逆運動學，得到32 組完備逆解集。Sakata 等人基于梯度投影法提出了一種空間冗余機械臂的避障路徑規劃算法，該方法主要利用冗余機械臂自運動的特點實現其實時的避障路徑規劃。

本文針對冗余機械臂的特點，在對已知任務空間運動求關節空間逆解的基礎上，引入機械臂與障礙物之間的虛擬排斥速度場，從虛擬排斥速度作用點處將機械臂拆成2 段并聯的機械臂分別求解關節空間避障角速度分量，并向零空間投影得到自運動角速度分量，最后加上完成末端主運動的最小范數求得完整避障速度解，最終獲得機械臂避障運動軌跡。

1 冗余機械臂

本文的研究主體為Kinova Gen3 型七自由度冗余機械臂，機械臂的結構如圖1 所示。

圖1 7 自由度冗余機械臂Fig.1 7-DOF redundant manipulator

建立機械臂的標準D-H 參數模型，見表1。

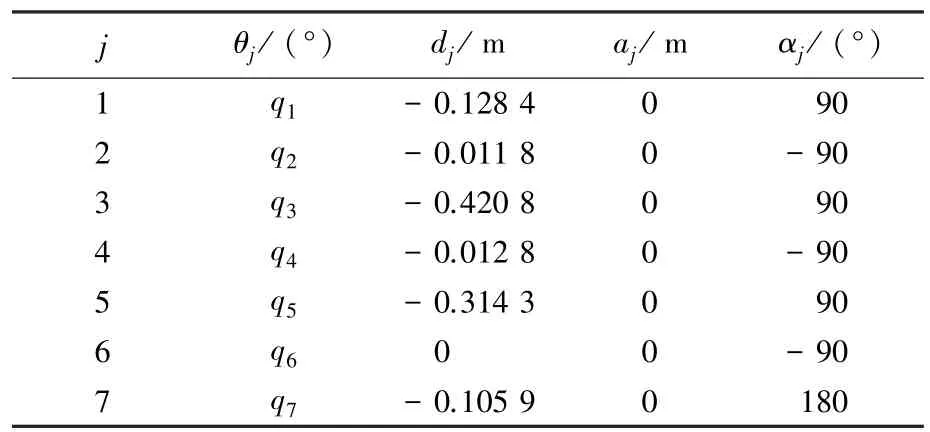
表1 機械臂D-H 模型參數Tab.1 D-H model parameters of the manipulator

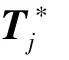
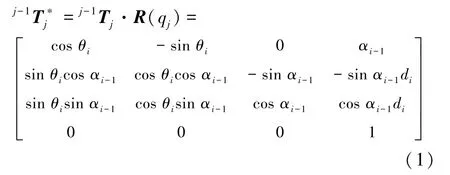
其中，T為第-1 關節到第關節坐標軸變換矩陣，（q）為第關節坐標系在關節角q下的旋轉矩陣。

機械臂的第1、3、5、7 關節軸向與連桿延伸方向平行，第2、4、6 關節軸向與連桿延伸方向垂直，第1、3、5、7 關節所連接的2 段連桿不會在空間結構上發生變化，故在碰撞檢測時可將機械臂視作4 段串聯機械臂分別計算，繞桿軸向轉動作用可等效至桿件兩端。

2 關節角速度的最小范數解

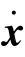
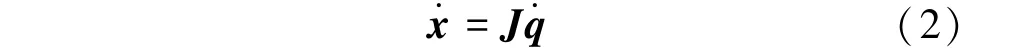
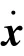
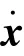
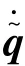
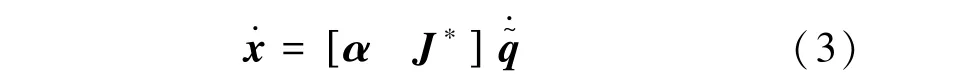
其中，為由的個線性無關的列重新排列組成的非奇異矩陣；為中除去組成列向量以外的部分。

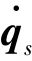
3 冗余機械臂零空間自運動避障

利用冗余機械臂可以在關節空間齊次解所在的零空間自運動而不影響末端執行器位姿的特性，可實現一定程度的避障功能。本文提出一種通過在機械臂與障礙物之間構建虛擬排斥速度場獲得排斥速度作用點以及該點的避障排斥速度，進一步地，將機械臂視為末端在排斥速度作用點的并聯機械臂，由逆運動學求解各個關節的避障速度，最后向零空間投影，得到一組利用自運動實現避障的關節速度解。

3.1 碰撞檢測

障礙物可能具有不同的形狀，可近似地看作規則幾何形狀的組合，使用超二次函數描述障礙物的表面，在笛卡爾坐標系下，曲面方程可表示為：

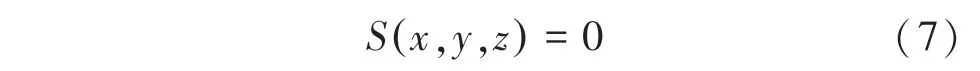
滿足上式的點（，，）組成的集合即為該曲面。對于幾何中心為O（，，）、幾何參數為，，的典型障礙物，其曲面可采用如下解析表達式進行描述：

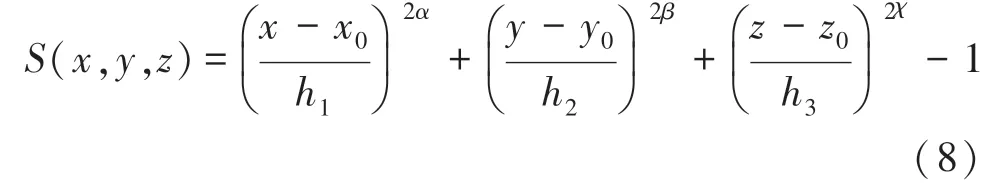
其中，通過改變冪指數，，的值，得到不同形狀障礙物；通過改變，，的取值，改變障礙物中心的位置；通過改變，，的取值，可以表述具有不同輪廓大小的障礙物。

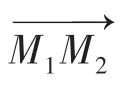
其中，是一個常系數（0 ≤≤1）。機械臂上最近點X由參數λ表示的坐標可以通過最小偽距離求出。表面方程在基系下可以表示為：

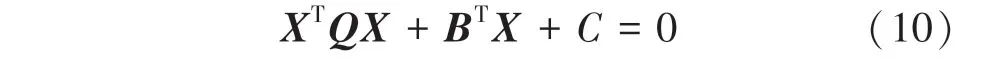
其中，矩陣、向量和標量是常量。任意點在笛卡爾空間中的偽距離為：

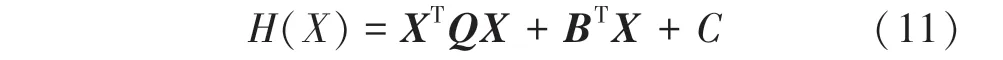
代入機械臂上任意一點表達式：

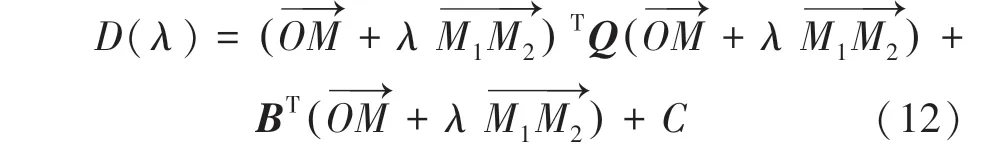
可以等價地寫成：

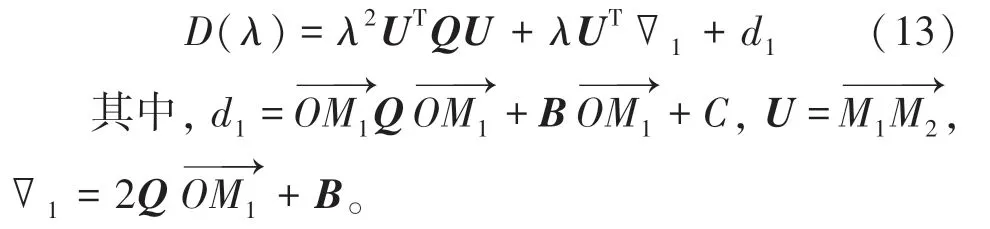
當上式對的導數為0 時有最小偽距離：

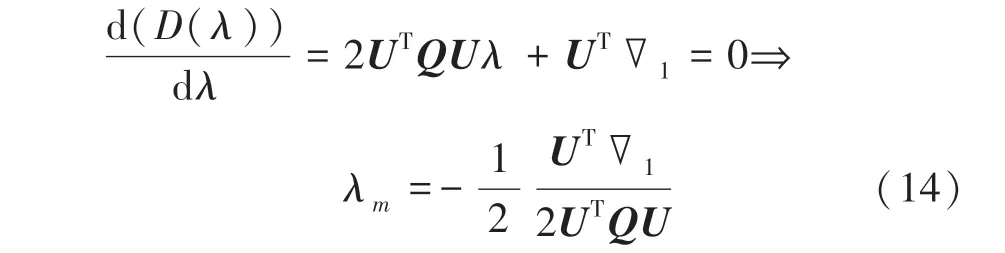
若λ ＜0，則令λ取值為0，此時X就是點；若λ ＞1，則令λ取值為1，此時X就是點。

將得到的桿與障礙物最近點X代入到偽距離函數（）中確定唯一的防碰撞條件約束：

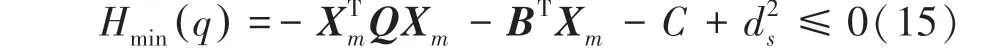
其中，d為安全距離。

3.2 虛擬排斥速度場構建

在基系笛卡爾空間內構建冗余機械臂與障礙物之間的排斥速度場，如圖2 所示。

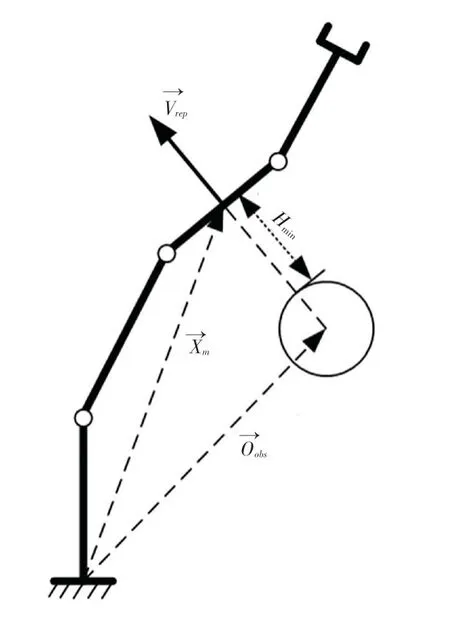
圖2 虛擬排斥速度場示意圖Fig.2 Schematic diagram of virtual exclusion velocity field

當機械臂與障礙物之間最近距離趨于0時，排斥速度趨于無窮大。

3.3 關節空間避障速度分量求解

將機械臂拆分為以排斥速度作用點為末端執行器的2 段并聯機械臂，分別命名為機械臂，機械臂，如圖3 所示。

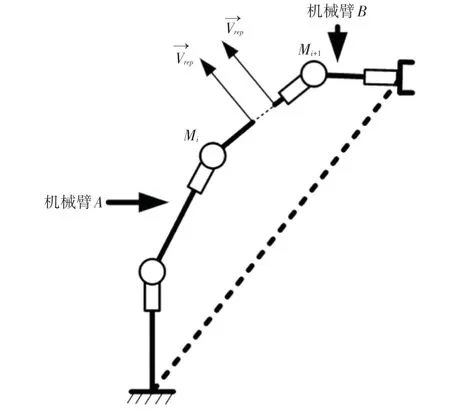
圖3 拆分后的2 段并聯機械臂示意圖Fig.3 Schematic diagram of two parallel manipulator after splitting

由Kinova Gen3 型機械臂的結構將機械臂整體視為4 段連桿，每個關節具有2 個自由度，排斥速度作用點處坐標系在機械臂、下的坐標變換分別為T，T。當排斥速度點作用于原機械臂基座至第一關節和最后一個關節至末端執行器之間的連桿時，機械臂不存在自運動，作用于當中的任意一點時T，T有統一表達式：

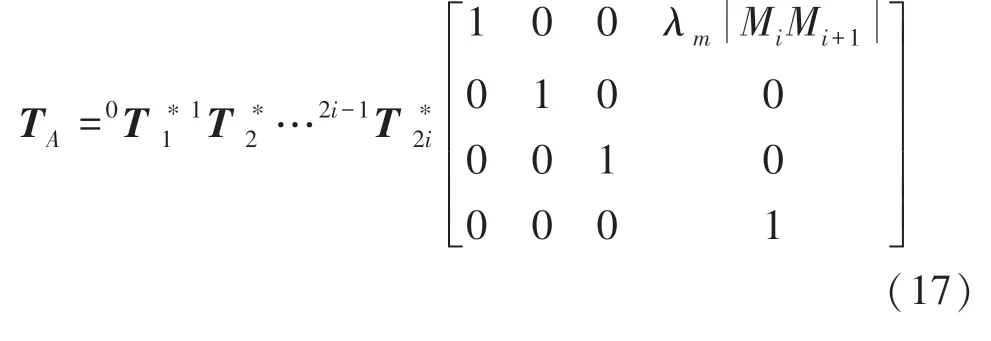
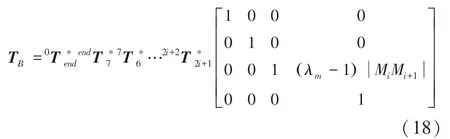
由于已知當前各個關節角度，故可直接解出T，T，進一步地可得到2 段機械臂在當前時刻的雅可比矩陣J、J。又因為原機械臂自由度為7，分成的2 段機械臂不是冗余機械臂，故可直接解出各關節的排斥速度分量：

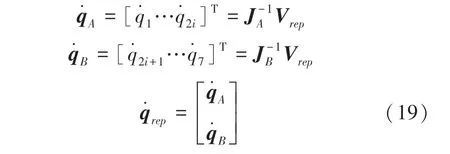
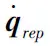
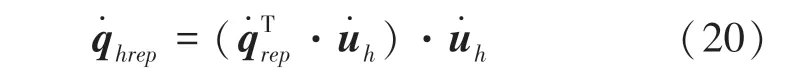
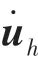
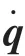
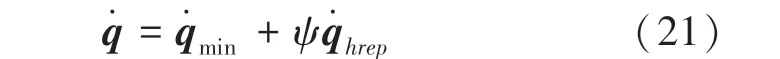
其中，為任意常數，對全時刻關節角速度進行積分得到各關節角度值，重復上文循環計算至末端到達終點，最終獲得一條能實現末端軌跡跟蹤，并同時具備避障能力的冗余機械臂關節空間軌跡。

4 仿真試驗

4.1 仿真環境

為了驗證算法效果，本文基于Kinova 公司Gen3型七自由度冗余機械臂，在Matlab R2020b 環境下進行仿真試驗。

機械臂初始位姿設置各個關節角度為［90°，15°，180°，230°，10°，55°，90°］，運動目標為使末端執行器在笛卡爾空間相對位移［0.4 m，0.4 m，-0.4 m］，并繞軸與軸旋轉60°在基系笛卡爾空間內設置2 個障礙物，幾何中心坐標為［0.2 m，0 m，0.5 m］，［-0.1 m，-0.4 m，0.8 m］，障礙物包絡球半徑為0.05 m，機械臂連桿半徑0.03 m。

4.2 仿真試驗結果與分析

試驗首先根據末端執行器目標位姿，利用五次多項式插補出一條末端軌跡，再進行逆運動學關節角速度求解，同時計算本文提出的虛擬排斥速度場下避障角速度分量，至此積分計算關節角度解，獲得完整軌跡。冗余機械臂的運動過程如圖4 所示。整個運動過程平穩，末端執行器成功到達目標位姿，過程中未與障礙物發生碰撞。

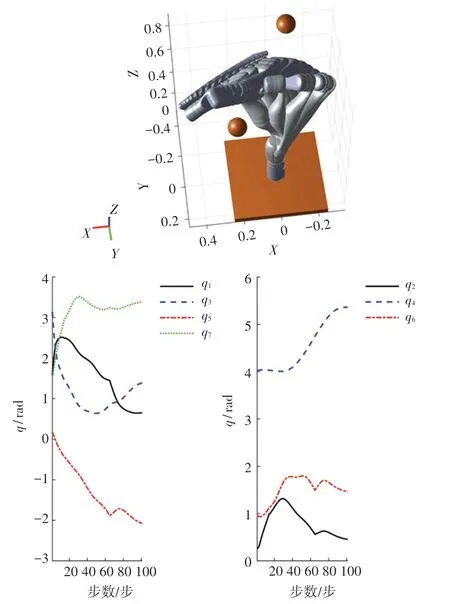
圖4 機械臂運動過程Fig.4 The movement process of the manipulator

為了驗證算法是否具部避障功能，記錄整個過程中的障礙物與機械臂最近距離、虛擬排斥速度大小、以及虛擬排斥速度引起的避障角速度分量。避障關節角速度分量變化如圖5 所示。

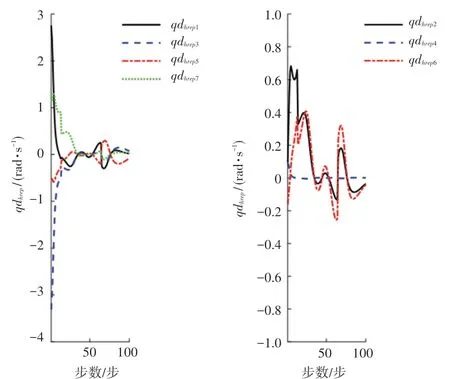
圖5 避障關節角速度分量Fig.5 The angular velocity component of the joint for obstacle avoidance

障礙物與機械臂最近距離以及虛擬排斥速度大小對照如圖6 所示。

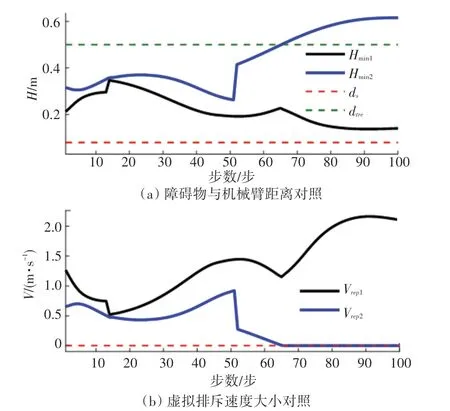
圖6 障礙物與機械臂距離對照及虛擬排斥速度大小對照Fig.6 The distance between the obstacle and the manipulator was compared with the virtual rejection speed

兩者在整個運動過程中呈鏡像變化趨勢，當大于建立的虛擬排斥速度場范圍d時，虛擬排斥速度V大小為0，當小于安全距離d時，認為發生碰撞。仿真試驗過程中，機械臂與障礙物距離始終大于安全距離，機械臂在成功運動至目標位姿的同時，實現了避障。

5 結束語

本文提出的冗余機械臂的軌跡規劃算法，不僅能有效完成末端執行器的軌跡跟蹤任務，同時還利用了冗余機械臂自運動的特性實現了避障，在障礙物周圍建立虛擬排斥速度場，將冗余機械臂從與障礙物最近的虛擬排斥速度作用點處分成2 段并聯機械臂，對于本文的研究對象、七自由度冗余機械臂，拆分后的機械臂都不冗余，故可快速求解在虛擬排斥速度作用下的關節角速度分量。同時結合改進梯度投影法快速求解實現末端執行器主運動的最小范數解，達到冗余機械臂實時軌跡規劃的目的。