基于BP-LSTM 組合神經網絡模型的汽車車速預測

王維強，于金泉，周一鶴，嚴運兵

（武漢科技大學 汽車與交通工程學院，武漢 430065）

0 引言

隨著智能交通出行的發展需求，道路信息實時預測變得越來越重要，神經網絡通過自身學習為汽車車速預測提供了新的解決方案。汽車的能量管理策略可以結合神經網絡、機器學習等方法對路況信息進行實時預測，大大提高能量管理策略的效率，改善發動機的工作區間，優化整車能量分配，降低故障發生率。如果提前預知汽車在未來時刻的行駛狀態，如車速、需求轉矩等信息，便能運用全局優化算法控制車輛性能達到一定時域內的最優狀態。此外，預測汽車未來車速，可用于汽車路徑導航、碰撞預警及節能輔助駕駛系統，其研究具有重要的理論與應用價值。

近些年隨著機器學習的發展，不少學者使用基于數據驅動的方法對未來車速進行預測。牛超凡提出了基于BP 神經網絡的短期車速預測器，實現車速的預測，未考慮BP 網絡容易陷入局部極值的問題。樓挺設計了遺傳算法優化的LSTM 神經網絡，用于道路車速預測，證明LSTM 在解釋時間序列的波動性上有明顯優勢。Epelbaum 等人融合多深度學習模型構建時間依賴的數據回歸模型，并將歷史速度數據匯總到網絡模型中，實驗結果表明該方法比單獨的深度學習模型具有更好的準確性。韓少劍等人建立了混合深度學習的工況預測模型，并利用STL 分解算法實現對車速的預測。提升了車速預測的準確性，但是由于結構復雜、算法繁瑣，大大增加了預測時間，導致預測效率較低。

單一模型的預測方法很難滿足多方面的要求，綜合考慮預測精度和預測效率兩方面因素，本文提出了BP-LSTM 組合神經網絡模型。其中，BP 神經網絡具有出色的非線性映射能力且結構簡單，模型訓練時間較短，將其放在組合神經網絡模型的第一層。LSTM 揭示了時間序列的本質，是處理時間序列數據的常用方法，將其放在第二層。訓練集數據首先利用BP 進行訓練，訓練集數據和得到的殘差序列輸入到第二層LSTM 網絡中，Adam 算法優化LSTM 網絡的權值和閾值。把2 種神經網絡的優點結合起來，降低了網絡復雜度，提高模型訓練效率的同時，增強預測精度。本文以東風華神R401 純電動載貨汽車監測數據為基礎，利用深度學習框架Tensorflow 進行模型的搭建與驗證，證明此組合神經網絡模型預測精度優于BP、LSTM 單模型，對汽車車速預測有重大意義。

1 神經網絡理論基礎

1.1 BP 神經網絡基本原理

BP 神經網絡（Back Propagation Neural Network，BPNN）、即反向傳播神經網絡，由輸入層、隱藏層、輸出層組成，各層之間的神經元是全連接，層內各個神經元無連接，網絡結構如圖1 所示。

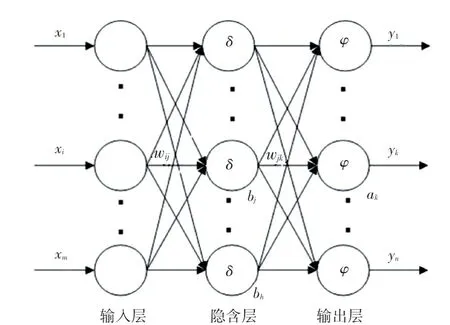
圖1 BP 神經網絡結構Fig.1 BP neural network structure

在圖1 中，x表示輸入層第個神經元的輸入，1，2，…，；w為輸入層第個神經元到隱含層第個神經元的連接權值，1，2，…，；隱含層第個神經元閾值記為b；隱含層激活函數為；w為隱含層第個神經元到輸出層第個神經元之間的權值，1，2，…，，輸出層第個神經元的閾值為a，輸出層的激活函數為；y為輸出層第個神經元輸出。

BP 神經網絡算法有正向傳播、反向傳播兩個過程，并利用梯度下降法，通過反向傳播來不斷調整網絡的權值和閾值，使誤差平方和最小。其原理和學習過程如下。

（1）正向傳播過程。隱含層第個神經元的輸入net和輸出h分別為：

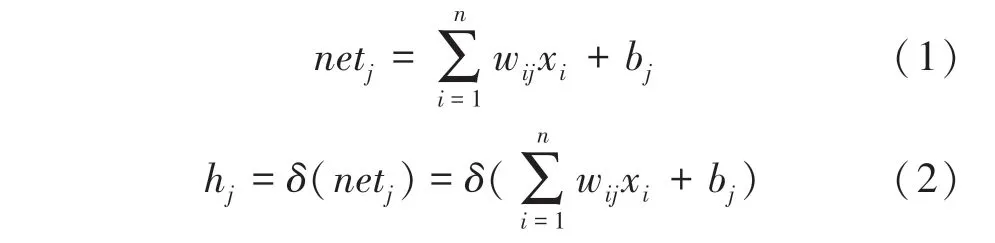
輸出層第個神經元的輸入net和輸出y為：

（2）反向傳播過程。得到輸出層輸出y后，利用反向傳播的思想來調整參數，減少網絡訓練迭代次數，提高模型訓練準確性。對于每一個樣本，設其輸出層第個節點的期望輸出為T，則此樣本的二次型誤差目標函數E為：

定義損失函數（），可以表示為：

1.2 LSTM 神經網絡

LSTM 通過控制緩存中的值保存的時間來記住更長期的信息，有效解決了當連續數據的序列變長、反向傳播更新參數時，梯度消失或梯度爆炸等問題。其核心在于引入自循環的思想，以產生梯度長時間持續流動的路徑，在處理和時序相關的問題上具有較好的效果。

LSTM 網絡有輸入門限、遺忘門限、輸出門限三個門控單元，網絡結構如圖2 所示。

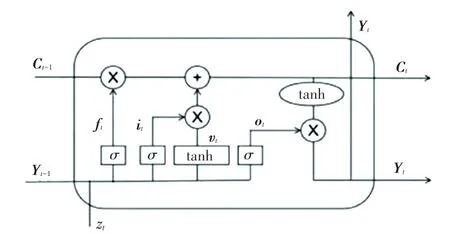
圖2 LSTM 神經網絡結構Fig.2 LSTM neural network structure

由圖2 可知，LSTM 神經網絡中各組成部分的設計功能擬做闡釋與解析如下。

（1）遺忘門f：決定哪些信息被遺忘，哪些信息通過細胞狀態。公式如下：

其中，W是遺忘門權重矩陣；Z為當前時刻負載；b表示偏置向量；表示激活函數。

（2）輸入門i：通過激活函數來決定哪些值用來更新，并保留到下個狀態單元中。2 個神經元i和v計算公式如下：

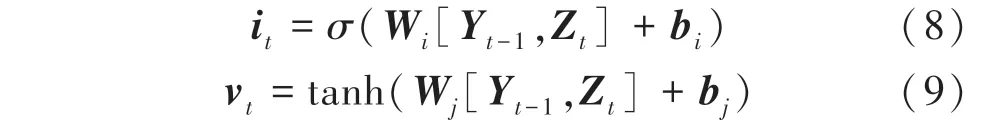
其中，W、W是輸入門權重矩陣，b和b為偏置向量。

生成更新后的神經元狀態信息C的數學公式可寫為如下形式：

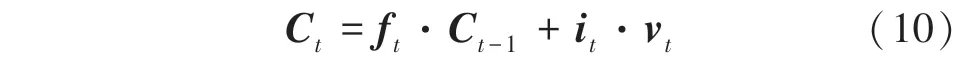
（3）輸出門o：計算當前信息輸出到下一時刻的程度，決定著模型的輸出。此處需用到的數學公式為：

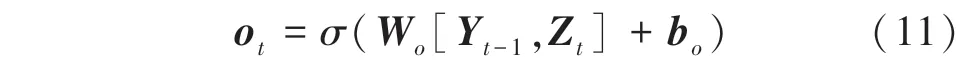
其中，W為輸出門權重矩陣，b為偏差向量。

當前時刻神經元的輸出Y可由如下數學公式計算求出：

2 組合神經網絡模型設計

通過統計分析和大量的實驗可以看出，當前的道路交通狀況對后續的交通狀況有很大的影響，并且連續時間段內的車速狀況之間存在較強的時間序列關系。

2.1 模型設計

本文提出的組合模型網絡結構有2 層。第一層采用BP 網絡，BP 網絡結構簡單，訓練速度快，能提高預測效率，但是其在處理時間序列上精度不如LSTM，故模型第二層采用LSTM，并用Adam 算法優化LSTM。輸入端接入BP 神經網絡，預測輸出和殘差作為LSTM 的輸入，在提高網絡的非線性映射能力的同時降低過擬合的概率，前一時刻的輸出值參與下一時刻的計算，增強對車速的識別與預測。本文設計研發的組合神經網絡結構如圖3 所示。

圖3 中，z、z表示BP、LSTM 神經網絡隱含層神經元，y為BP 網絡輸出層的神經元， y′為預測殘差，f、i、o分別表示輸入門、遺忘門、輸出門， Y為模型輸出。

圖3 BP-LSTM 組合神經網絡結構Fig.3 BP-LSTM combined neural network structure

汽車行駛在同一工況時，當下及未來一小段時域內汽車車速和前幾個時間段的車速有關，利用神經網絡的自學習能力，構建出組合神經網絡模型，忽略緊急情況的影響。定義為采集報文信號的時間間隔。

令為預測時間，v為第個時間間隔中采集到的車速信息，車速序列可表示為：

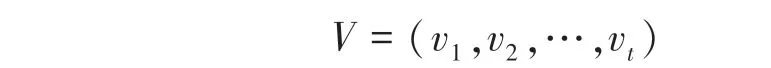
記組合模型輸入序列、輸出序列分別為：

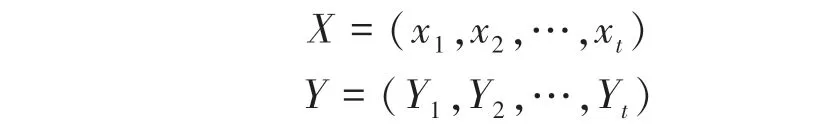
采集10 min 內的車速數據，為200 ms，設置為180000 ms，使用前2400 個數據對模型進行訓練，后600 個數據對模型進行測試驗證。這里的組合預測模型參數見表1。

表1 組合預測模型參數表Tab.1 Parameters table of combined prediction model

2.2 基本原理

BP 神經網絡模型接受來自訓練集數據的輸入，通過梯度下降算法不斷修正權值w和閾值b，反復訓練最后輸出預測結果y和預測殘差y′，二者共同輸入到后端LSTM 模型中，LSTM 再對輸入進行訓練，其中LSTM 模型內使用自適應矩估計（Adaptive moment estimation Adam）算法，核心即是矩估計思想和動量衰減，Adam 通過計算梯度的一階矩估計和二階矩估計給不同的參數設計獨立的自適應性學習率，算法設計表述見如下。

選取2017年9月—2018年9月在我院建卡進行產前檢查和分娩的286例高齡產婦作為研究對象，所有產婦均為單胎妊娠，年齡≥35歲，孕周37～42周。其中203例妊娠結局正常為對照組，83例不良妊娠結局為觀察組。

2.3 模型預測流程

綜合預測精度、預測效率（以運行時間為準）兩方面因素，考慮BP 神經網絡和LSTM 神經網絡各自優勢，提出了BP-LSTM 組合神經網絡模型實現汽車車速預測，預測流程如圖4 所示。對此，文中給出研究詳述如下。

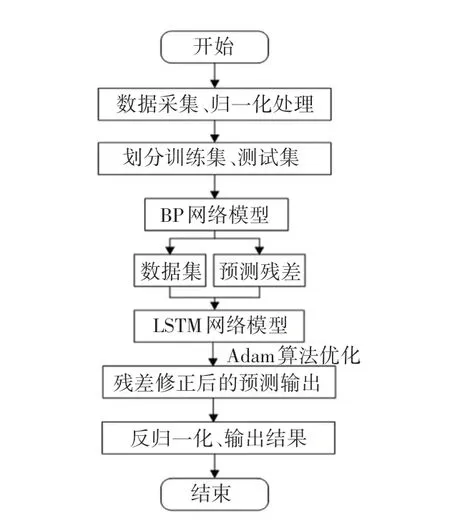
圖4 預測流程圖Fig.4 Prediction flow chart

（1）把采集到的數據進行數據增強、歸一化處理，然后把數據集隨機分成并無交集的訓練集、測試集，各占80%、20%，最后For 循環遍歷整個訓練集，配成輸入特征、輸入標簽對，送入樣本。

（2）Python 語言設計BP 神經網絡，初始化權值、閾值，輸入訓練集、測試集，訓練BP 網絡模型，得到最優模型參數，輸出預測值和預測殘差。

（3）利用Python 語言、深度學習框架Tensorflow進行LSTM 神經網絡模型搭建，接收來自上一層BP神經網絡的輸入，利用LSTM 優化預測殘差，此處的LSTM 神經網絡中引入Adam 算法。

（4）最終的預測結果為BP 網絡預測結果加上LSTM 修正后的預測殘差。

3 仿真結果和分析

3.1 數據采樣及預處理

對于汽車車速預測問題，歷史車速將作為最重要的輸入，因此汽車歷史數據的采集對車速預測的準確性影響很大。為了驗證汽車在頻繁啟停工況下車速連續變化時組合模型的準確性，特采集東風華神R401 純電動載貨汽車在連續急加速、急減速時的行駛信息，收集到的信號根據CAN 通信協議進行解碼處理，解碼后的部分信息見表2。

表2 解碼信息表Tab.2 Decoded information table

汽車車速數據具有波動性、復雜性，數據預處理是以數據為驅動的機器學習算法應用中重要的環節。本文所使用的汽車車速數據，不可避免地會出現一些異常數據，對于這些數據，要及時地調整、剔除。把剩下的數據和時序數據一一匹配，此后經過清洗、歸一化處理后得到增強數據集，作為組合模型的輸入數據。

3.2 模型訓練環境及評價指標

為了客觀準確地評價提出BP-LSTM 網絡結構對汽車車速的預測效果，本文選定均方根誤差（）和平均相對誤差（）作為預測精度評價指標，以模型學習、預測總時間衡量預測效率。本文給出的數學定義具體如下。

（1）均方根誤差（）。指預測值與真實值偏差的平方和與觀測次數比值的平方根，表征了預測的精確度。公式如下：

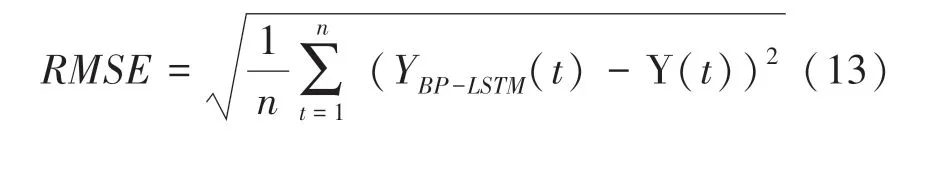
（2）平均相對誤差（）。表征了樣本數據離散程度，公式如下：

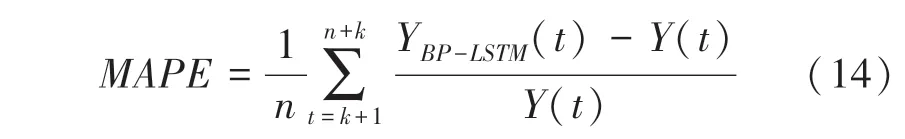
其中， Y（）和（）分別表示BP-LSTM網絡的預測車速和真實車速。

3.3 模型預測及對比分析

為了驗證本文所提出的混合神經網絡方法的有效性，將BP-LSTM 組合神經網絡預測結果分別和BP、LSTM 神經網絡算法進行結果對比分析，并通過均方根誤差和平均相對誤差兩個評估指標的計算值來評判預測模型的性能。

采集報文信號的時間間隔為200 ms，取過去10 min 的車速數據，共3000 個。預測時間間隔設定為3 min，把上述數據輸入到BP 單模型中，得到的結果如圖5 所示。

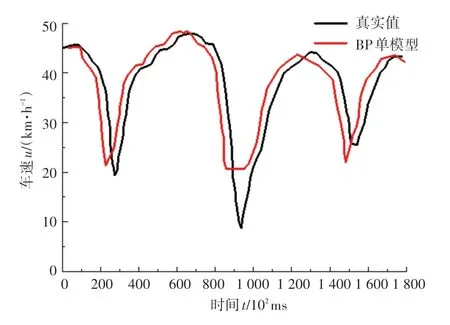
圖5 BP 神經網絡預測結果Fig.5 BP neural network prediction results

由圖5 中可以看出，BP 模型預測結果反映了真實值的變化趨勢，但是也存在較高的延遲，且對急劇變化時的車速不敏感。將同樣的數據放進LSTM 模型中，得到的預測結果如圖6 所示。

圖6 LSTM 模型預測結果Fig.6 LSTM neural network prediction results

由圖6 不難看出，LSTM 模型的預測結果相較于BP 模型有了很大提升，二者擬合效果更好，在車速呈近似線性變化時效果最理想，但在車速變化呈非線性時仍有提升空間，而且在車速最低、且急劇變化時預測效果不理想。針對此現象，根據組合神經網絡模型設計思路，把相同的數據輸入到BP-LSTM組合神經網絡模型中，得到的預測結果見圖7，損失結果見圖8。

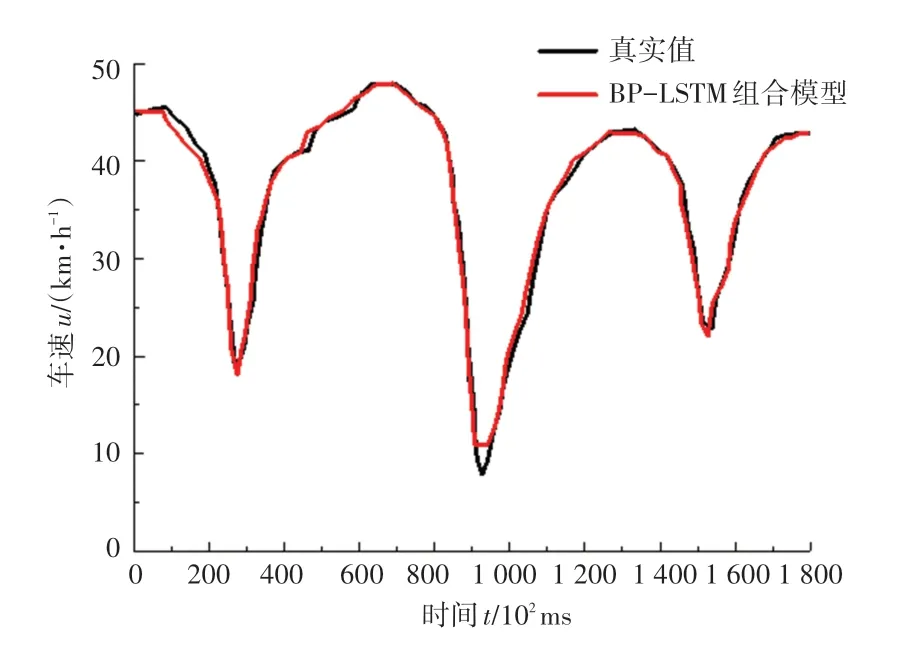
圖7 BP-LSTM 模型預測結果Fig.7 BP-LSTM neural network prediction results

圖8 BP-LSTM 模型預測損失結果Fig.8 BP-LSTM neural network prediction loss results

從圖7 中可以看出，組合模型在預測精度上表現得比前2 種單模型要好，預測的車速擬合了真實車速的變化趨勢。從圖8 中可以看到，真實數據損失大多一直處在0.0002 和0.0006 之間，迭代次數為10 次時，真實損失突然升高。隨著迭代次數的增加，預測損失一直在0.004 范圍，基本上保持不變。預測誤差始終在一較低范圍浮動，也說明了組合神經網絡模型在預測車速方面的準確性和穩定性。

3 種模型的預測誤差指標和組合神經網絡模型相比于2 種單模型的預測指標降低百分比則詳見表3、表4。

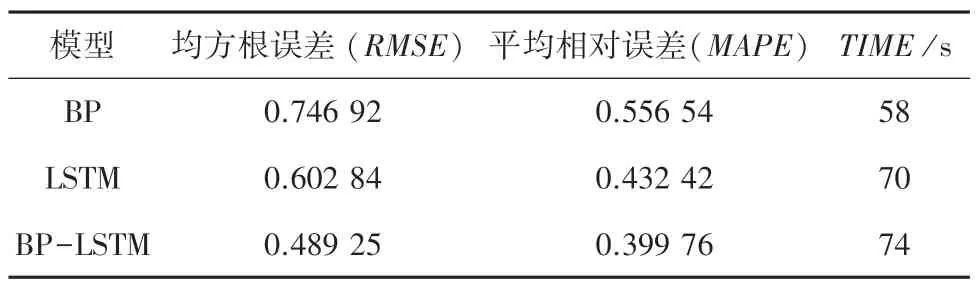
表3 3 種模型預測結果對比Tab.3 Comparison of prediction results of the three models

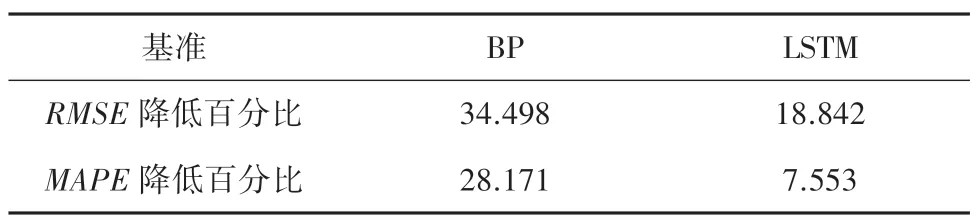
表4 組合神經網絡預測指標降低百分比Tab.4 Percentage reduction in combined neural network predictors%

由表3 中可以看出，BP-LSTM 組合模型的預測結果與實際車速數據二者之間的均方根誤差為0.48925，平均絕對誤差為0.39976，遠遠小于BP、LSTM 的誤差數值。誤差在可接受范圍內，反映了汽車未來3 min 內的趨勢，準確完成了車速預測。組合神經網絡預測模型用的時間長于2 種單模型，但是用時增加的百分比低于精度提升的百分比。此外，根據表4 可知，組合模型在均方根誤差、平均相對誤差上相比BP 單模型分別降低了34.498%和28.171%；相比于LSTM 模型分別降低了18.842%、7.553%，預測精度得到明顯提高。

3.4 對比實驗及分析

為了說明組合模型的可適用性，使用另外一種數據集驗證仿真，采集報文信號的時間間隔為200 ms，取過去10 min 的車速數據，共3000 個。預測時間間隔設定為3 min，把上述數據輸入到BP-LSTM模型中，誤差損失曲線如圖9 所示。

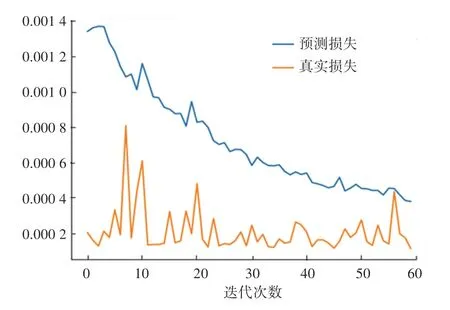
圖9 BP-LSTM 模型預測損失結果Fig.9 BP-LSTM neural network prediction loss results

從圖9 可以看到，真實數據損失一直處在0.0002和0.0004 之間，隨著迭代次數的增加，預測損失在逐步下降，最終接近于真實數據損失。剛開始預測損失較高的原因可能是出現了過擬合現象，隨著BP神經網絡模型不斷迭代和LSTM 神經網絡模型對預測殘差的不斷優化，使得預測誤差逐步減小，最終和真實損失誤差一致。

4 結束語

綜上所述，通過建立BP、LSTM、BP-LSTM 三種神經網絡模型，利用Python 語言實現對應算法，對不同數據集進行仿真分析和對比驗證，得出本文提出的BP-LSTM 組合神經網絡模型相較于單一模型，在預測精度、訓練穩定性上有較大的提高，使用不同的數據集，也能保證預測誤差在一較小范圍內，提出的BP-LSTM 組合神經網絡模型在汽車車速預測方面具有更高的準確度。