分層設計習題 　凸顯精準練習

葉群芳

《義務教育數學課程標準（2011年版）》中指出：要充分提供有趣的、與兒童生活背景有關的素材，以適當的方式呈現給學生，讓學生經歷應用數學知識提出問題、分析問題和解決問題的過程。同時適當增加些開放性的綜合應用的內容，以有利于學生自主探索、合作與交流。根據這個標準我把一節數學課的習題設計分成四個層次：

一、以鞏固為底色的基礎性練習

第一層次是基礎性的習題，側重知識的內化——落實習題的教學、檢查等功能。

“面積和面積單位”是三年級下學期“空間與圖形”的內容，是學生學完“周長”后的再學習。學生從長度到面積，是從一維空間向二維空間的轉化，是空間形式“由線到面”的一次飛躍。在學習了面積概念、面積單位以及長方形、正方形面積計算后，設計了這樣一組基礎習題：

1.在括號內填上合適的單位

（1）一本練習本的長約21（? ）。

（2）一本練習本封面的大小約2（? ）。

（3）一棵大樹高約10（? ）。

（4）一棟樓房的占地面積約100（? ）。

2.填空

1米=（? ）分米? ?1平方米=（? ）平方分米

20厘米=（? ）分米? 500平方分米=（? ）平方米

10米=（? ）厘米? ?10平方分米=（? ）平方厘米

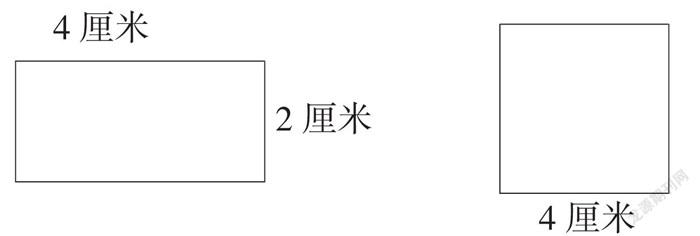
3.計算下面圖形的周長和面積。

【設計意圖】第一題是對面積內涵的分析。周長是對一維空間（線）的度量，面積是對二維空間（面）的度量，一個平面圖形往往同時存在著周長和面積，學生初始的認知容易混淆兩個概念。通過對合適單位的填寫，讓學生體會練習本的長是對長度的測量，只能選擇長度單位;而練習本封面的大小則是對一個面大小的測量，只能選擇面積單位。

第二題是換算單位練習。面積與周長最本質的區別是概念內涵不同，但顯性表現就在單位名稱和計算方法的不同上。將長度單位和面積單位的換算同時在一題中呈現，就是讓學生通過對比練習，進一步鞏固相鄰的長度單位之間的進率為10，而相鄰的面積單位之間的進率卻是100。

第三題是計算方法的對比練習。看似簡單的公式運用，本質上卻是對周長與面積概念的進一步辨析。長方形的周長是圍成長方形一周的長度，所以是四條邊長度的和;而長方形面積卻是面的大小，是鋪在長方形面上所有面積單位的和。這是從一維空間向二維空間轉化的對比練習，是實現學生空間意識“由線到面”的一次跨越。

二、以運用為底色的變式練習

第二層次是靈活的變式習題，側重知識轉化為技能一一落實習題的運用功能。

基礎練習是針對例題的再現，是學生思維的同化過程，但學生的思維能力需要在變式、靈活的訓練中形成。在練習中比較周長和面積的不同是防止概念混淆，促成概念精確分化，厘清概念內涵的有效措施。為此，設計了這樣一組練習：

1.填空

（1）長方形的長10分米，寬比長短4分米，長方形的周長是（? ），面積是（? ）。

（2）正方形的周長是20厘米，它的面積是（? ）。

（3）長方形的周長是24厘米，寬是3厘米，它的面積是（? ）。

2.判斷題

（1）正方形的邊長為4厘米，它的面積和周長相等。（ ）

（2）周長相等的兩個長方形，面積也相等。（? ）

（3）周長相等的兩個正方形，面積也相等。（? ）

3.解決問題

（1）用一根長14米繩子圍一個長4米的菜園，這個菜園的面積是多大？

（2）在一個長15米，寬50分米的長方形地里種玉米，如果每平方米約收玉米3千克。這塊地共收玉米約多少千克？

（3）一個長方形菜地周長20米，長8米，一邊長靠墻，這個長方形菜地的面積是多少平方米？

【設計意圖】變式練習不再是簡單周長和面積的計算，是需要尋找解決問題時所需中間條件的練習，引導學生的思維從同化走向分化，從單一走向多元。

填空題分三個層次，第一小題只要算出寬，就能解題;第二小題要通過正方形周長計算出邊長，再計算正方形的面積;第三小題有一定的難度，需要通過長方形的周長÷2，算出一組鄰邊的和，再間接地算出長，練習中需要教師畫圖讓學生理解周長÷2，表示哪兩條邊的長度。

判斷題是對面積和周長概念的深度解讀。面積和周長是不同的兩個概念，不能因為數字一樣，就判斷兩者相等。周長相等的兩個長方形，判斷面積是否相等，需要引導學生畫圖舉例，并在直觀操作中理解。第三小題是對第二小題的補充，避免學生的思維固化。判斷題三個層次，互相補充、互相滲透，引導學生思維由單薄走向豐滿。

第三題是解決生活中的數學問題，引導學生在具體的實際應用中，解決周長與面積的現實問題。層層遞進，讓學生在變式中尋找條件，鍛煉了學生的思維，培養學生思維的靈活性。

三、以發展為底色的綜合性練習

第三層次是綜合性、發展性習題，側重知識的深化與優化——落實習題的綜合性、發展性等功能。

皮亞杰認為：“守恒是獲得數和量概念的重要條件，兒童沒有守恒概念就不能真正認識數和量。”這組練習就是依據皮亞杰所做的關于面積守恒的實驗。通過練習，使學生體會拼或者剪，不變的是什么，變化的又是什么。

1.填空

（1）3個邊長為1cm的正方形拼成一個長方形。拼成的長方形的周長是（? ），面積是（? ）。

（2）正方形的邊長擴大到原來的3倍，周長擴大（? ），面積擴大（? ）。D25CCD8F-1EE7-4402-AD22-8AF1B6F8DA7F

（3）一個長方形長增加5厘米，寬減少5厘米，它的周長（? ），面積（? ）。

2.解決問題

（1）一個長方形長20厘米，寬15厘米，在里面剪下最大的正方形，剪下的正方形的面積是多少？還可以提出什么數學問題并解決？

（2）一個長方形的長減少5厘米，面積就減少45平方厘米，這時剩下的部分恰好是個正方形。原來長方形的面積是多少平方厘米？

【設計意圖】練習的設計具有思考性、綜合性、發展性。需要學生具備扎實的基礎知識，再通過分析題目中給定的條件，根據面積的守恒規律，通過畫圖、實驗、推理，得出結論。三個1平方厘米的正方形拼成的無論是什么圖形，不變的肯定是面積，變化的是周長。正方形邊長、長方形長和寬的變化引起的周長和面積的變化是這部分習題的重點，解題策略是通過舉例、畫圖、操作、計算，發現規律，解決問題。

《義務教育數學課程標準（2011年版）》將增強學生發現和提出問題的能力，分析和解決問題的能力作為數學課程的總目標之一。為此，在解決問題中要加強學生發現和提出問題能力的培養，當學生完成剪正方形的任務后，有必要引導學生思考，還可以進行怎樣的計算，真正實現發現問題、提出問題能力的培養，把學習的主動權交給學生。

四、以創新為底色的實踐性練習

第四層次是應用性、實踐性的習題，側重知識的實踐性靈活應用——落實習題的開放、創新等功能。

《義務教育數學課程標準（2011年版）》中，將“應用意識”作為十個核心概念之一，同時指出，綜合實踐活動是培養學生應用意識的載體。為此，在教學中設計了應用面積知識解決生活中的數學問題的習題。

小青家廚房要鋪地磚，有兩種設計方案：

（1）第一種設計方案用了300塊地磚，這個廚房的面積是多少平方分米？合多少平方米？

（2）如果用第二種設計方案，需要多少塊地磚？

（3）哪種設計方案造價更便宜？

（4）你還能提出怎樣的設計方案？

【設計意圖】著名數學家波利亞在《怎樣解題》一書中，明確提出了解決問題的一般步驟：理解題目——擬訂方案——執行方案——回顧。

根據題意可知，兩種規格地磚大小和價格已知，由第一種設計方案可以計算出廚房的面積;借助計算出的廚房面積就能計算第二種方案地磚的塊數;由地磚塊數可以計算出兩種地磚的價格，并比較。擬定設計方案是個開放題，學生只要能設計出可行的方案都可以。如將二者拼接、組合，組成不同的圖案，都是學生的創新能力的體現。回顧整道題，這是集應用、事件、開放、創新為一體的練習，學生在練習中積累、在練習中成長、在練習中厚積而薄發。

分層設計習題，是根據學生思維發展的不同階段，設計符合其思維發展階段性特征的練習，是教師對所教知識有了全面的理解和把握、是對學生個性化學習的人文關照，更是對兒童學習數學真切需要的理解。D25CCD8F-1EE7-4402-AD22-8AF1B6F8DA7F