具有驅動容錯性的冗余并聯機構構型綜合

單彥霞 蘇開興 高雪原 李仕華

(1.燕山大學機械工程學院， 秦皇島 066004； 2.燕山大學里仁學院， 秦皇島 066004；3.燕山大學河北省并聯機器人與機電系統實驗室， 秦皇島 066004)

0 引言

并聯機構動平臺的運動依賴于所有分支的共同驅動，若并聯機構某一分支的驅動出現故障，機構動平臺的運動會出現失準、失控或失靈問題[1]。在機構學中，驅動容錯指機構在運行過程中驅動器發生故障，仍然能完成預定工作任務，并維持其性能不變或變化很小。因此，研究并聯機構的驅動容錯問題對減少驅動故障造成的工程損失具有重要意義。

20世紀80年代末，MACIEJEWSKI[2]研究了串聯機器人的可靠性與冗余容錯問題。MONTEVERDE等[3]提出了將四層次(關節、鏈路、子系統與系統)容錯方法應用于串并聯機器人。李波[4]針對冗余驅動航天器執行機構的故障，設計了2種姿態容錯控制方案。文獻[5-6]研究串聯機構的驅動故障容錯問題時，在梯度投影法中引入了加權最小范數法優化容錯軌跡規劃算法，并針對串聯機構提出了綜合關節可操作度的容錯能力評價指標。繆萍等[7]針對自由擺動類故障(其實質是驅動力失效或關節約束失效)提出一種通過優化運動軌跡規劃實現驅動容錯的方法，并研究了驅動容錯過程中驅動關節速度突變的影響因素。閆彩霞等[8]基于故障隔離的思想分別研究了冗余并聯機構的驅動器故障和非驅動關節故障對機構動力學性能的影響，并利用結構冗余和力矩再分配方法實現了冗余并聯機構的故障容錯。潘陽[9]針對一種雙并聯結構的6足并聯機器人，采用優化設計的驅動控制策略，研究了在鎖死故障和不可控故障下該機器人的驅動故障容錯性能。YAO等[10]研究了一種基于冗余自由度的并聯機構驅動容錯控制策略及對應的機構工作空間邊緣識測方法，并對大重型副反射鏡調節并聯機構進行了研究，有效提高了機構的工作可靠性和驅動容錯性。QU等[11]研究了一種三平移4-UPU冗余并聯機構驅動力失效問題，該機構在任一分支驅動力失效時機構移動能力不受影響，有較好驅動力失效容錯性。YI等[12]研究了3種關節失效類型對并聯機構運動學性能的影響，提出了一種利用工作空間和運動冗余的機構容錯方法。

綜上所述，關于并聯機構驅動容錯的研究主要集中在控制策略方面，也有通過結構冗余提高某一具體機構的驅動容錯性。但是，只是針對具體機構的研究，這類機構還不夠豐富，缺少具有驅動容錯性的冗余并聯機構構型綜合方法。本文提出一種針對分支驅動力失效故障的具有驅動力失效容錯性的冗余并聯機構構型綜合方法，綜合出多種該類型的并聯機構，以期為具有驅動容錯性并聯機構的應用奠定理論基礎。

1 驅動失效度評價指標

1.1 約束空間和驅動空間

并聯機構約束空間SCw為機構動平臺所受到的各約束力螺旋組成的螺旋系，可求解機構自由度空間的反螺旋得到，即

(1)

機構驅動空間SAw指機構的一組驅動力螺旋組成的螺旋系，用于描述機構所受到的驅動力，即

SAw={$A1w,$A2w,…,$Anw}

(2)

一般情況下，并聯機構驅動空間SAw的維數與自由度相等。若冗余并聯機構的驅動空間和約束空間線性無關，則機構所選驅動空間合理，稱之為“驅動合理判據”[13-14]。冗余并聯機構的自由度和約束度(約束空間的秩)之和仍為6。因此，當驅動力失效故障不影響機構約束性質時，只需維持機構驅動空間和約束空間的秩和為6的關系不變，可有效降低驅動力失效對機構運行的影響，即機構具有驅動力失效容錯性。

1.2 可操作性失效度指標

雅可比矩陣由驅動空間和約束空間組成。設支鏈型冗余并聯機構的自由度為n，分支數為q，每個分支上有且僅有1個驅動副，機構雅可比矩陣可表示為

(3)

雅可比矩陣與其共軛轉置矩陣積行列式的平方根為可操作性指標ω，計算式為

(4)

式中λi——雅可比矩陣的正特征值

為了量化分析驅動力失效對機構可操作性能的影響，基于雅可比矩陣，機構的可操作性失效度指標(Operability invalidity index，OII)為機構在相同空間位置或者姿態下，并聯機構分支i驅動力失效后可操作性變化量與失效前的可操作性之比，其表達式為

(5)

式中ζi——機構當前瞬時位姿下的可操作性失效度

ωJ——機構所有分支驅動正常時的可操作性

由式(5)可知，ζ越大機構在該位姿下的可操作性越差。

同時，為了準確評價力矩陣和力矩矩陣受驅動力失效的影響，式(5)還可以表示為

(6)

為了進一步衡量并聯機構在整個工作空間內的可操作性受驅動力失效的影響程度，定義全域可操作性失效度指標(Global operability invalidity index，GOII)，表達式為

(7)

2 構型綜合方法

2.1 驅動同一性條件

從驅動力螺旋的角度分析，若并聯機構在結構上具有一定驅動容錯性，則當機構中任一分支發生驅動力失效故障時，機構仍然能完成工作任務[15-17]。為了滿足“任一分支”的條件，機構分支的驅動力螺旋應具有“同一性”，即：冗余并聯機構的驅動力螺旋在固定坐標系下的表達為同一形式，且驅動空間線性無關數等于自由度，則去掉任一驅動力螺旋(驅動力失效故障)時，其驅動空間不會降秩，驅動空間具有驅動容錯性。

驅動“同一性”條件，是判斷機構是否具有驅動容錯性的一個充分必要條件。利用驅動空間的“同一性”條件既可以判斷機構是否具有驅動容錯性，也可以進行機構綜合，進而得到一類具有驅動容錯性的并聯機構。

2.2 構型綜合方法

基于驅動“同一性”條件，以滿足驅動力螺旋可互相替補為核心，具有驅動容錯性的冗余并聯機構構型綜合的基本流程如圖1所示，具體步驟為：

(1)確定機構自由度F、冗余驅動分支數目m和機構運動方式。

(2)確定機構自由度空間，得到機構單位自由度螺旋系St，并通過螺旋理論求得機構單位約束空間SCw。

(3)根據驅動合理判據，求解單位約束空間正交補，得到機構單位約束正交補空間SDw。對單位約束正交補空間進行擴展，得到能滿足驅動“同一性”條件的初始單位驅動力螺旋，并得到對應的初始驅動力螺旋組合$Aiw表達式。

(4)基于得到的初始驅動力螺旋組合，選擇對應的運動副，并從中確定驅動副。得到具體的驅動力螺旋，組成初始的驅動空間S′Aw。

(5)對初始的驅動空間進行擴展：根據冗余驅動分支數，添加滿足“同一性”條件的驅動力螺旋，得到可針對驅動力失效的具有驅動容錯性的驅動空間SARw。

(7)利用并聯機構自由度的修正G-K公式，根據預設的自由度n、分支運動副數等，計算分支自由度ki和運動副數gi以及過約束數ν之間的關系，確定在不同分支自由度數目下，機構的過約束數ν。

(8)根據機構的自由度要求，以及螺旋之間的相關性，對分支的運動副進行布置得到具體的機構，并使其滿足步驟(7)中得到的過約束數和分支自由度。

(9)應用螺旋理論綜合出的并聯機構具有運動瞬時性，因此對機構的過約束數和分支自由度進行全周性分析。

(10)利用提出的可操作性失效度指標對綜合得到的機構進行分析，并優化機構。

圖1 構型綜合流程圖Fig.1 Process of type synthesis

根據該類機構的綜合方法，可對不同自由度的具有驅動力失效容錯性的冗余并聯機構進行分析與綜合。

3 具有驅動容錯性的三轉動冗余并聯機構構型綜合

三轉動并聯機構在醫療康復和空間指向等領域應用較為廣泛，其自由度均為轉動，容易滿足驅動同一性條件[18-19]。以任意1個分支驅動力失效容錯的4分支三轉動類型并聯機構綜合為例，根據提出的機構綜合方法，其構型綜合過程如下：

(1)設機構自由度為3，取分支數目q為4，機構進行球面轉動，并且動平臺繞定點轉動。

(2)由設定自由度得到單位自由度空間為

(8)

求反螺旋得到單位約束空間為

(9)

(3)機構約束為3個約束力，限制機構的3個移動自由度。根據驅動合理判據，計算單位約束空間的正交補，得到機構約束正交補空間為

(10)

(4)確定運動副應為R副、U副或S副，并選擇其中與定平臺相連的R副為驅動副。

(5)對式(10)驅動力螺旋添加冗余驅動螺旋，得到具有驅動容錯性的驅動空間為

(11)

其中

(6)由式(11)驅動空間得到機構約束空間為

(12)

由式(12)可知，機構約束力螺旋為空間匯交于一點的3個約束力線矢，限制機構的移動自由度。

機構運動副全部為R副時，R副對動平臺的驅動力螺旋為力偶，力偶方向可根據R副軸線方向確定。為了滿足驅動同一性條件，R副的軸線應匯交于一點，保證驅動失效時的“可替性”。

(7)自由度分析。由G-K自由度公式可得

(13)

得到的分支組合存在5種情況，如表1所示。為避免累述，以第1種情況為例進行詳細描述。

表1 分支運動副布置情況Tab.1 Layout of branch joints

當分支數為4且分支結構相同，設分支自由度為3，即分支有3個R副。根據前述分析，機構有12個約束力，約束了3個移動自由度，存在9個過約束。由線幾何判據，空間匯交于一點的約束力，其線性無關度為3。為保證同一性，該點到各個R副的距離應相等，相應地有以下3種方案：

(1) R副軸線匯交于定、動平臺中心點連線的中點，該點到各個R副的距離一致，記為Ⅰ型，如圖2a所示。

(2) R副軸線匯交于定平臺中心，但4個分支的布置為空間分散布置，記為Ⅱ型，如圖2b所示。

(3) R副軸線匯交于動定平臺之外的某定點，記為Ⅲ型，如圖2c所示。

圖2 R副布置方案Fig.2 Arrangements of rotating pairs

當分支存在U副時，分支過約束要求為9，此時無論如何布置都不能使得機構的過約束滿足條件，因此情況1時分支無U副。

分析可知，不能滿足自由度條件的情況為：① 分支中含有2個及以上U副。② 分支的過約束度小于0。③ 分支運動副數最多與最少的差值超過2。

對所有滿足自由度性質的分支進行排列組合并進行全周性分析，即分支自由度性質不會隨著機構的運動而發生變換。可綜合得滿足布置要求(約束螺旋匯交一點)的機構有39種，如表2所示。部分機構結構簡圖如圖3所示。

由表2可知，綜合出的分支構型組合只有5種完全對稱，其驅動容錯性也最理想，選擇(4-RRR)Ⅰ冗余并聯機構作為實例進行驅動容錯性分析。

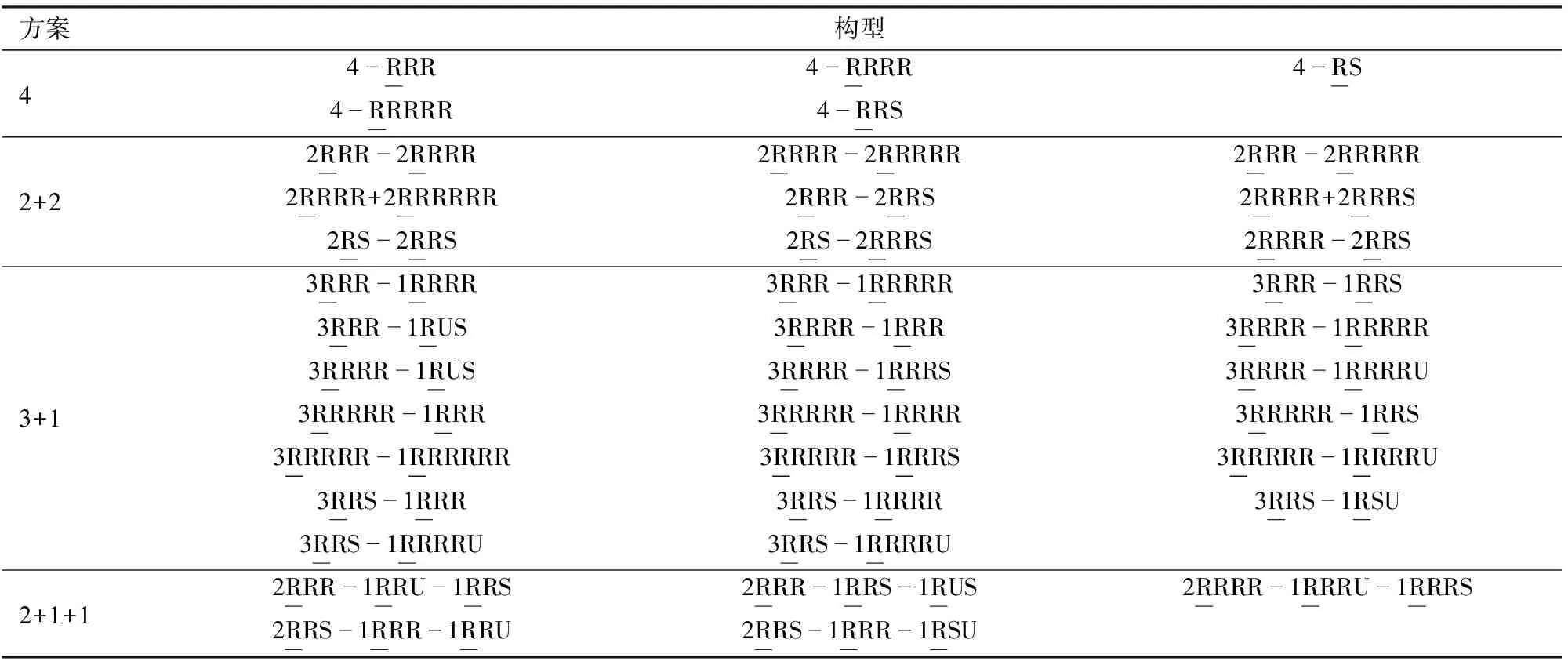
表2 具有驅動容錯性的三轉動冗余并聯機構Tab.2 3R DOF redundant PMs with actuation fault tolerance

圖3 綜合得到的部分冗余并聯機構結構簡圖Fig.3 Synthesized partial redundant PMs

4 (4-RRR)Ⅰ機構驅動容錯性分析

4.1 運動學分析

(4-RRR)Ⅰ冗余并聯機構由2個大小不等的圓形平臺以及4個完全相同的RRR分支構成。所有R副的軸線匯交于動定平臺中心點連線的中點處；以與定平臺相連的4個R副為驅動副；每個分支的3個R副的中心點依次標記為Ai、Bi、Ci(i=1,2,3)。(4-RRR)Ⅰ機構三維模型和建立的基坐標系OXYZ、動坐標系OpXpYpZp如圖4所示。

圖4 (4-RRR)Ⅰ冗余并聯機構Fig.4 (4-RRR)Ⅰ redundant PM

定平臺中心點為OA，設OOA和OOp長度分別為rA、rp。設與定平臺相連的R副軸線與定平臺平面夾角為φR，與動平臺相連的R副軸線與動平臺平面夾角為φr；分支各桿件半徑為RL、桿弧度為φL，動、定平臺半徑為r、R。

為防止機構奇異位形，動定平臺形狀相同但半徑不同，設機構參數之間的關系如表3所示。

表3 (4-RRR)Ⅰ冗余并聯機構結構參數關系Tab.3 Structural parameters of (4-RRR)Ⅰ redundant PM

由機構位置可知，各分支的點Bi2與Ai1、Ci3之間存在幾何關系：lOAi1與lOBi2垂直，lOCi3與lOBi2垂直。

各分支第1個R副在基坐標系下單位運動螺旋為

(14)

各分支第2個R副在基坐標系下的單位運動螺旋為

(15)

其中

式中li2、mi2、ni2——各個分支中間R副軸線方向單位向量

各分支第3個R副在基坐標系下的單位運動螺旋為

(16)

其中

式中li3、mi3、ni3——各個分支與動平臺相連的R副軸線方向單位向量

求反螺旋易得該機構在基坐標系下的單位約束空間為

(17)

設機構動平臺的3個姿態角為α、β、γ，利用Z-Y-X描述，得到機構姿態矩陣TO為

TO=rot(γ,z)rot(β,y)rot(α,x)=

(18)

式中s表示正弦函數，c表示余弦函數。

根據選定的驅動副，即與定平臺相連的R副為驅動副，求得機構單位驅動空間為

(19)

其中

式中li、mi、ni——各分支驅動力單位方向向量

各分支的單位驅動力力螺旋為同時垂直于lOBi與lOCi方向的單位力偶。

設分支的輸入值為θi(i=1,2,3,4)，進而結合機構的單位驅動螺旋系和單位約束螺旋系得到機構的雅可比矩陣為

(20)

4.2 驅動容錯性分析

由式(20)可知，當機構任一驅動力螺旋失效時，機構雅可比矩陣秩恒定不變。即機構自由度不發生變化，機構可正常工作。

根據1.2節可操作性失效度指標的定義，利用雅可比矩陣，由式(6)計算得到機構的可操作性失效度圖譜，即FOII圖譜和MOII圖譜，分別如圖5、6所示。

圖5 FOII圖譜Fig.5 FOII atlas

由圖5可知，(4-RRR)Ⅰ機構的FOII在單分支驅動力失效后無變化。機構的MOII在個別位置變化較大，這與該位置姿態角和R副軸線角度有關。該MOII圖譜表明單個分支的驅動力失效對機構動平臺的可操作性影響較小。

圖6 MOII圖譜Fig.6 MOII atlas

(4-RRR)Ⅰ機構的GOII為22.628 3%，以OII和GOII不高于30%為具有驅動容錯性的標準[20]，(4-RRR)Ⅰ機構具有驅動容錯性。但是，(4-RRR)Ⅰ機構在某些位置下的MOII起伏較大，整體性能較差，可優化R副軸線角度、機構轉動中心點位置，連桿弧度等結構以進一步提高機構性能。

5 結論

(1)針對驅動力失效故障，提出了一種具有驅動容錯性的冗余并聯機構構型綜合方法。

(2)從理論上解釋了機構如何針對驅動力失效進行容錯的條件，即驅動“同一性”條件。

(3)利用提出的構型綜合方法綜合了一類三轉動冗余并聯機構，得到了39種構型。

(4)通過評價綜合出的(4-RRR)Ⅰ機構的驅動容錯性，驗證了所綜合出的冗余并聯機構針對驅動力失效具有驅動容錯性。