雙模融合6-[(RPRRRP)R-R]US并聯機構運動學分析

陳宇航 趙鐵石 郭建綱 陳麗緩 郝增亮

(1.北華航天工業學院機電工程學院， 廊坊 065000；2.燕山大學河北省并聯機器人與機電系統實驗室, 秦皇島 066004;3.燕山大學先進鍛壓成形技術與科學教育部重點實驗室, 秦皇島 066004)

0 引言

多任務協同、多模式融合是機械裝備發展的趨勢。為應對復雜的實際應用，機構學領域涌現出一系列新穎的機構形式，如可重構機構、并聯冗余自由度機構和含有子閉環的機構等。并且針對多模式并聯機構、多任務融合機構、一機多用等方向開展了較多研究。

關于可重構機構、多模式機構等研究成果較多，戴建生團隊[1-2]首先闡述了變胞機構的機理和應用，并對相關研究進展進行了系統梳理；于靖軍等[3]論述了多模式機構的研究進展以及未來應用的可能；單彥霞等[4]基于TCI指標提出一種能實現多模式機構操作模式平穩切換的方法。劉偉等[5]基于自由度可變的混聯支鏈綜合了一類多模式機構，能實現3種運動模式間的變換。沈惠平等[6]提出了一種動平臺可重構的三自由度并聯機構，具有部分運動解耦性。鄒琦等[7]設計了一種運用離合器與齒輪系配合完成機架重構過程的并聯機構。石志新等[8]采用方位特征集法對四自由度雙模式機構展開綜合，并對其中一種進行位置分析。具有冗余自由度的機構，運動輸出具有更多可能性。QU等[9-10]提出一種具有冗余自由度的平面機構，并進行了運動學和奇異性分析；ZHAO等[11]提出一種具有冗余自由度的并聯機構，由于運動的冗余特性使該機構具有非常大的轉角工作空間；GOSSELIN等[12-14]先后提出一類新型的具有轉動能力不受限制的平面冗余自由度并聯機構，以及一類能夠通過冗余特性消除奇異位形并增大轉動工作空間的空間機構。在分支中引入子閉環機構，可以改善空間機構性能，并能夠合理引入冗余自由度。LI等[15-16]對一類分支含子閉環的并聯機構進行研究，通過在分支內引入子閉環綜合一類少分支多自由度形式的并聯機構，并為步行機器人設計了一種含閉環結構的支腿；朱小蓉等[17]綜合了一類分支中含有雙驅動五桿閉環回路的并聯機構，并提出了7種耦合度為0的回路。文獻[18-19]面向調姿隔振應用，在并聯機構的分支中引入子閉環機構使原機構具有冗余自由度，并通過子閉環實現高低頻混合輸入。

多模式機構更多關注不同模式間的切換，而多模式融合應用在實際工程中應用同樣廣泛，本文拓展多模式機構的范疇，設計一種分支內含有六桿子閉環輸入單元的新型并聯機構，通過解析與數值相結合的方法對機構進行運動學分析，以期實現“高頻低幅值”與“低頻大幅值”兩種模式運動的融合。

1 機構形式

在6-RUS并聯機構中，各分支轉動副R為輸入。通常對輸入副R的實際驅動形式有電機直接驅動和四桿機構間接驅動，如圖1所示直接驅動形式，運動學計算相對簡單，但動力學性能較差；間接驅動形式，運動學分析較復雜，但動力性能較好。

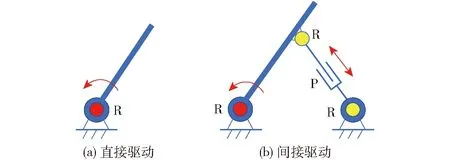
圖1 轉動副R的驅動形式Fig.1 Driving forms of rotating pair R

圖2 雙輸入單元組成原理Fig.2 Dual-input unit composition principle

為實現動平臺雙模融合運動，對驅動副R的驅動形式進行雙模融合輸入設計，其實現形式為在驅動副桿件的適當位置，通過另一個轉動副R′與一個平面六桿子閉環機構(RPRRRP)連接，構成雙輸入單元如圖2所示；也可以將該設計理解為將驅動副R替換為一個局部并聯機構，該局部并聯機構包含一個驅動分支和一個約束分支，其中約束分支只包含一個R副，驅動分支為包含一個平面六桿機構的混聯分支，形式為(RPRRRP)R。

根據Kutzbach-Grübler公式[20]計算可得(RPRRRP)R-R雙輸入單元的自由度為2，需要兩個輸入，機構才能有確定運動。以兩個P副為實際輸入，它們分別對應兩種運動模式的驅動，因此通過雙輸入單元的輸出桿可實現雙模運動融合。

通過上述方法實現雙模融合輸入后，機構形式為6-[(RPRRRP)R-R]US，如圖3所示。顯然雙輸入局部并聯機構的輸出桿件即為原6-RUS機構的原動件，且運動形式仍為原輸入副R的轉動，因此對于動平臺，約束形式與6-RUS相同，所以動平臺仍能實現空間六自由度運動。對于6-RUS機構，此時驅動副R的輸入中包含兩種成分，分別對應雙輸入子閉環中兩種性質的驅動，可根據應用需求進行組合。每個[(RPRRRP)R-R]US分支需要雙輸入，總體機構才能具有確定運動，因此6-[(RPRRRP)R-R]US并聯機構自由度數為12，輸入數大于末端構件自由度數，屬于運動冗余并聯機構。

圖3 機構形式及坐標系Fig.3 Mechanism form and coordinate system

對該機構的分析，可以將機構劃分為內、外兩層，內層機構：(RPRRRP)R-R雙輸入子閉環機構；外層機構：6-RUS。內、外層機構通過共同的R副實現運動和力的傳遞。

2 單模式機構運動學反解分析

機構由動平臺、基座和6條形式相同的分支組成，每條分支與上平臺通過球副連接，鉸接點記為Bi，其中i為分支標號，i=1,2,…,6；分支底部與基座通過2個R副和1個P副連接，其中2個R副的鉸接點記為Ai、Fi。在Ai、Fi所在平面的幾何中心建立基坐標系{o},在Bi所在平面的幾何中心建立動平臺坐標系{m},如圖3所示。

每個分支中包含兩個驅動副，通過鎖定其中一個驅動，可讓機構工作于單一運動模式，以靈活適應不同應用場景。

雙輸入子閉環機構簡圖如圖4所示，將左側移動副設定為調姿驅動，對應一類低頻大行程驅動器，例如電動缸、液壓缸等；右側水平移動副設為振動驅動，對應一類高頻小行程驅動器，如作動器、高頻直線電機等。

2.1 調姿模式運動學反解

當振動驅動被鎖定，機構僅實現低頻小幅值的位姿運動。機構的運動學反解分為兩步：①對外層6-RUS并聯機構進行反解求得各分支輸入角θi。②建立內層驅動子閉環的運動學方程，根據θ求得實際驅動l1。

步驟(1)：不考慮驅動子閉環RPRRRP，外層機構形式為6-RUS，分支簡圖如圖5所示，建立分支坐標系{i}，R副與基座鉸接點Ai為坐標原點。

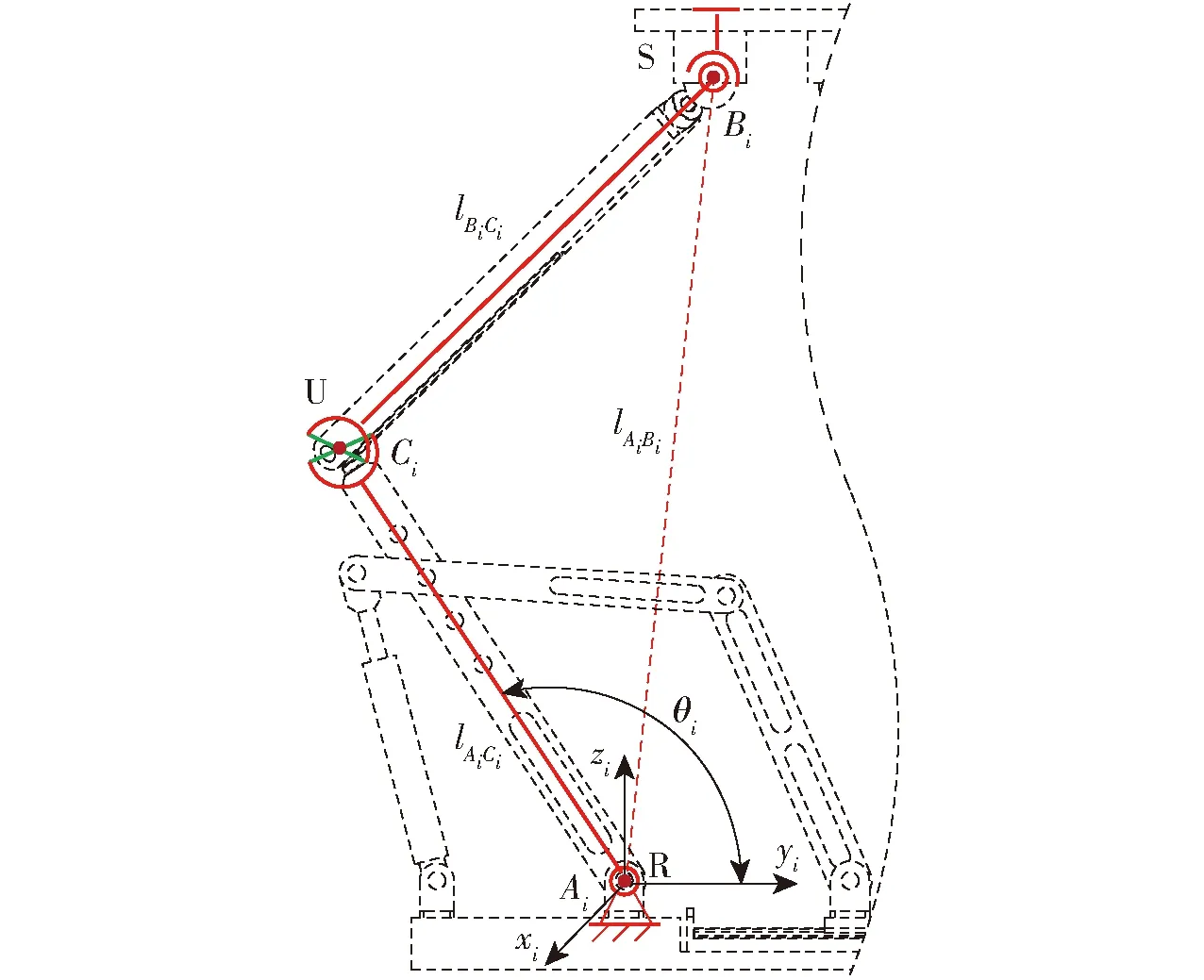
圖5 RUS單分支簡圖Fig.5 Simple diagram of single branch of RUS

根據桿長約束關系可得

(1)

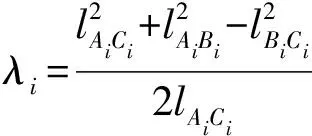
(2)

式中lAiBi、lAiCi、lBiCi——桿AiBi、AiCi、BiCi的長度

xBi、yBi、zBi——鉸鏈點Bi的坐標

步驟(2)：雙輸入單元機構簡圖如圖6所示。由于任意分支內雙輸入單元的計算過程相同，為了表達式簡潔，除驅動變量外，其余忽略分支下角標i。

圖6 雙輸入子閉環機構簡圖Fig.6 Mechanism diagram of dual-input sub closed loop

圖6中，l1i、l6i(i=1,2,…,6)是兩個驅動尺寸，即第i分支內FG、AE長度，l0、l2、l3、l4、l5分別為桿FA、GH、HD、DE、AH的長度，α為FG與水平方向夾角，β為桿DE與水平方向夾角，γ為桿GD與水平方向夾角。在調姿運動模式下，l1是變量，l6是定值。

根據幾何關系建立雙輸入子閉環機構的矢量封閉方程

l5+l3=l6i+l4

(3)

解得

(4)

其中

(5)

式中ku1、ku2、ku3——中間系數

點D和點H坐標為

(6)

(7)

令

(8)

式中yG——點G的y軸坐標

zG——點G的z軸坐標

K——桿GD斜率

由桿長l2約束關系可得

(9)

驅動量尺寸FG的長度關系式為

(10)

將式(8)、(9)所求值代入式(10)，即求得此時的實際驅動量l1i。

2.2 振動模式運動學反解

當調姿驅動被鎖定，機構輸出六維振動。此時圖6中，l1i是固定值，l6i是變量。其運動學反解同樣分兩步，步驟1與調姿模式相同，參照式(1)；步驟2為根據θ求得實際驅動l6i。

類似調姿運動求解過程可得α與θ的關系式為

(11)

其中

(12)

式中kv1、kv2、kv3——中間系數

點D坐標表示為

(13)

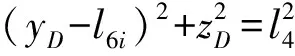
(14)

當動平臺位姿已知，由步驟(1)求得外層機構6-RUS驅動角θi，然后根據式(11)、(13)依次求得角α和點D坐標，最后通過式(14)解得振動模式的驅動輸入l6i。

3 雙模式融合運動學反解分析

機構進行雙模融合運動時，驅動輸入個數為12，動平臺輸出運動自由度數為6，屬于自由度冗余機構。對于給定位姿，可以得到無窮多組反解。結合一般實際應用工況，設定兩種反解求解策略，使得到的反解具有更為明確的實際意義，具體如下：

任意時刻t，動平臺輸出的融合運動位姿，可分解為兩種成分：低頻大范圍的位姿運動和高頻小幅值的振動，即

W(t)=Wu(t)+Wv(t)

(15)

式中W——雙模式融合運動位姿

Wu——位姿運動成分

Wv——振動成分

雙模融合運動可理解為一種平衡位置不斷改變的振動，變化的平衡位置即是位姿運動。因此在反解計算中，可以設定兩種驅動求解分配策略：

(1)先Wu(t)后Wv(t)：先求平衡位置后疊加振動

先求解任意時刻t平衡位置Wu(t)的對應的反解輸入，即調姿輸入，再以Wu(t)為當前平衡位置，求解機構從Wu(t)運動到W(t)的位姿反解，即振動輸入，過程如下：

假定各分支內振動輸入l6i在驅動中位鎖定，l6i的中位值作為求解l1i時一項固定的結構參數。以Wu(t)為目標位姿計算任意時刻t調姿輸入的值，即

L1(t)=L1(0)+u(t)

(16)

其中

(17)

式中L1——調姿輸入矢量

u——調姿輸入增量矢量

ui——l1i的增量

以Wu(t)為當前位姿，Wu(t)+Wv(t)為目標位姿，L1(t)為結構參數，根據振動模式的反解過程計算該t時刻振動驅動尺寸為

L6(t)=L6(0)+v(t)

(18)

其中

(19)

式中L6——振動輸入矢量

v——振動輸入增量矢量

vi——l6i的增量

在求L6的過程中，L1為時變結構參數，t時刻對應的值為L1(t)。

(2)先Wv(t)后Wu(t)：先求振動再改變平衡位置

以初始位置為平衡位，求解任意時刻t的振動位姿Wv(t)所對應的輸入，即振動輸入，再求每一時刻，機構從Wv(t)運動到Wu(t)+Wv(t)對應的反解輸入，即調姿輸入。該策略為策略(1)的對偶過程，具體步驟為：

先鎖定L1以其為固定參數，并以Wv(t)為目標位姿，計算任意時刻振動輸入L6(t)，再以L6(t)為瞬時結構參數，t時刻，以Wv(t)為初始形位，W(t)為目標形位計算L1(t)。

需要注意兩點：①兩種求解策略的先后順序僅是計算邏輯的先后，實際操作時，任意時刻計算得到L1(t)和L6(t)后，兩者同時輸入系統。②相同位姿下，兩種策略計算的雙輸入結果不同，設定的兩種策略所解算出的是機構無窮多組解中的兩組，但調姿輸入和振動輸入各自的反解模型不變。

4 機構運動學正解分析

已知機構的實際輸入L1(t)、L6(t)，求動平臺的位姿W(t)為機構正解。由于各分支內存在子閉環機構，因此機構正解同樣需要分兩步完成。

(1) 內層子閉環機構正解

任意分支i內，外層機構6-RUS的分支驅動角θi是關于l1i、l6i的函數，然而θi=f(l1i,l6i)的解析解難以獲得。因此采用數值方法求取。當l1i確定，θi隨l6i變化呈單調遞增關系，因此可以把l1i先給定，采用二分法迭代對比l6i，最終獲得滿足誤差允許要求的解。求解過程如圖7所示。

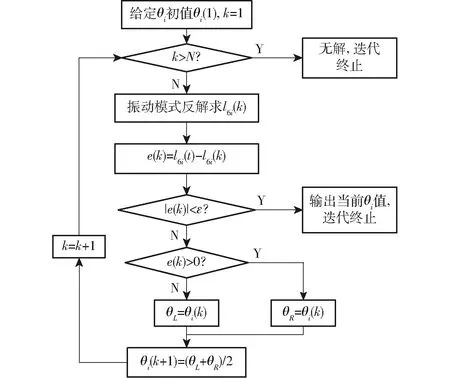
圖7 內層子閉環正解流程圖Fig.7 Process of positive solution in sub-closed loop

圖7中，N為最大迭代次數；e(k)為l6i第k次迭代誤差，θL、θR為當前循環下θi取值的邊界；ε為設定的求解精度。

(2)外層6-RUS機構正解

根據各分支子閉環內實際驅動，通過步驟(1)求得子閉環輸出桿的轉角θ，即外層6-RUS機構分支的驅動角。對于6-RUS機構，全部輸入θi已知，求動平臺的位姿W(t),為機構正解過程。

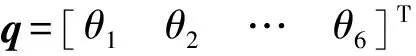
q=f(W)

(20)

方程組(20)為非線性方程組，根據輸入q求位姿W，解析方法難以求解，因此考慮采用數值法。為了讓求解過程快速收斂，可采用牛頓法[21]，迭代方程為

Wk+1=Wk+G(Wk)qΔk

(21)

其中

qΔk=q-f(Wk)

(22)

式中Wk——第k次迭代位姿

qΔk——q的第k次迭代誤差

G——機構一階影響系數

外層6-RUS機構正解流程如圖8所示。

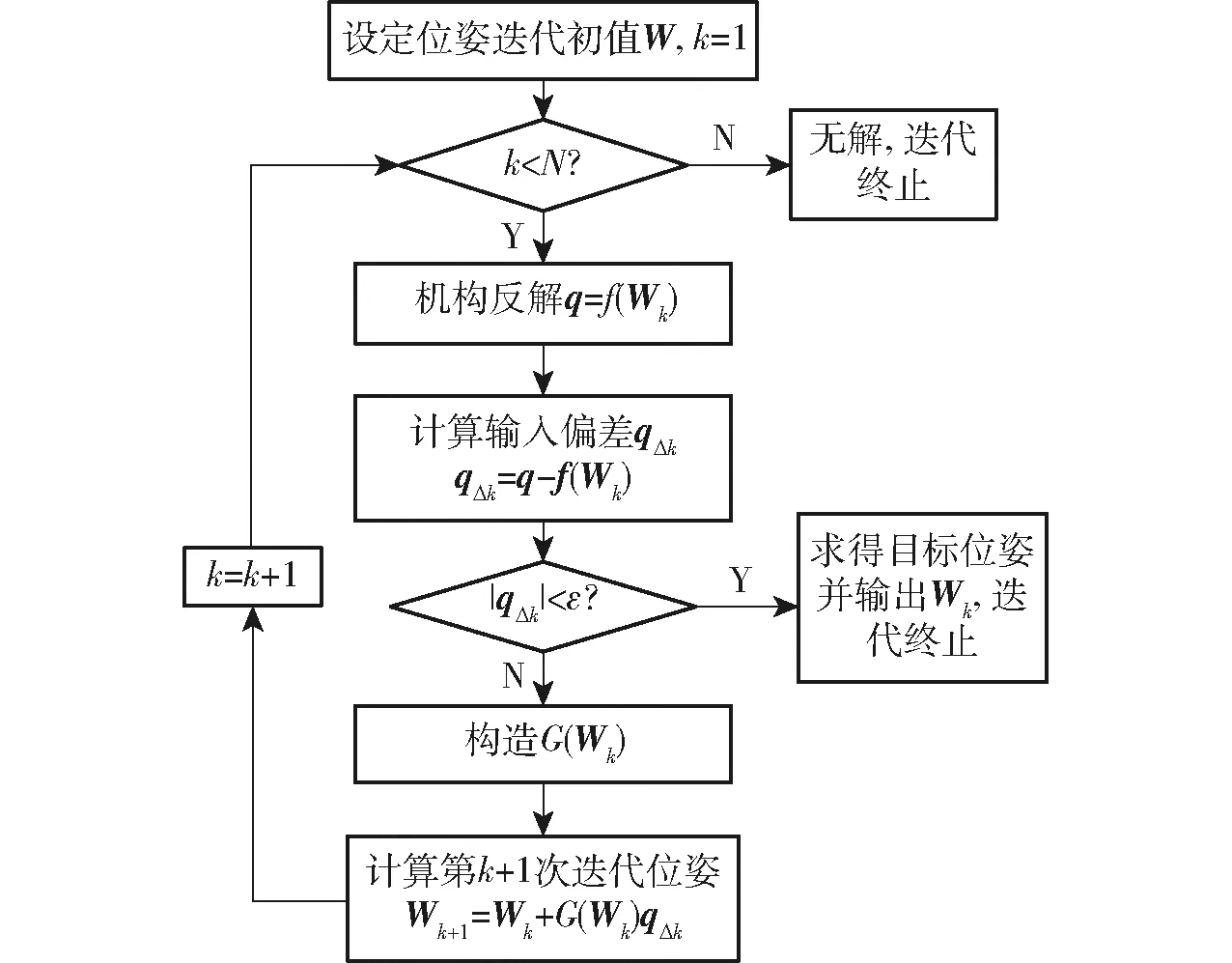
圖8 6-RUS機構正解流程圖Fig.8 Process of forward solution of 6-RUS mechanism

5 數值算例與仿真

通過理論模型計算和運動學仿真分別對上述理論分析正確性進行驗證。不同的反解分配策略得到僅是無窮解中的一組，因此只需按一種策略進行驗證即可，本文按先Wu(t)后Wv(t)策略進行。

5.1 機構結構參數

動平臺與基座鉸鏈點尺寸如圖9所示。

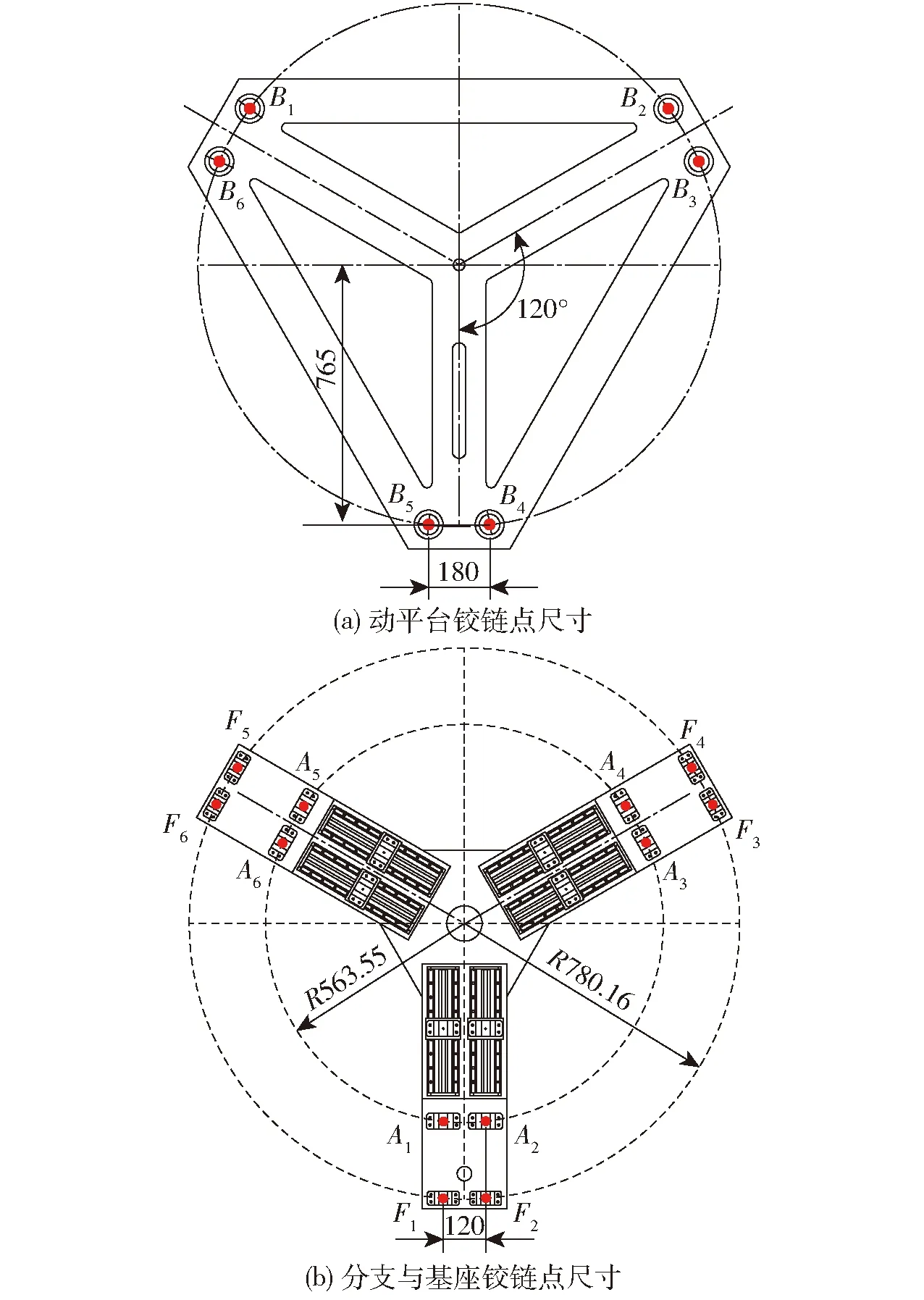
圖9 鉸鏈點分布尺寸圖Fig.9 Distribution dimension diagram of hinge points

驅動分支內各桿件尺寸見表1。

根據上述參數建立機構三維模型，并導入ADAMS中進行運動學仿真。

表1 桿件尺寸參數

5.2 單自由度運動融合算例

首先驗證機構在單一輸出自由度方向上的運動融合能力，機構具有6個輸出自由度，分別為3轉動和3移動，任取其中2個單自由度運動作為數值算例。不失一般性，選取x軸方向轉動和y軸方向轉動為例。

(1)繞x軸方向轉動

給定動平臺單軸雙模融合運動規律為

(23)

其中

rx(t)=r1x(t)+r2x(t)

(24)

式中rx——x軸角位移

r1x——x軸角位移位姿運動分量

r2x——x軸角位移振動分r1x(t)=10°sin(0.4πt)，r2x(t)=1°sin(2πt)，按先Wu(t)后Wv(t)規則，計算l1i(t)和l6i(t)的驅動增量u(t)和v(t)，理論值如圖10所示。

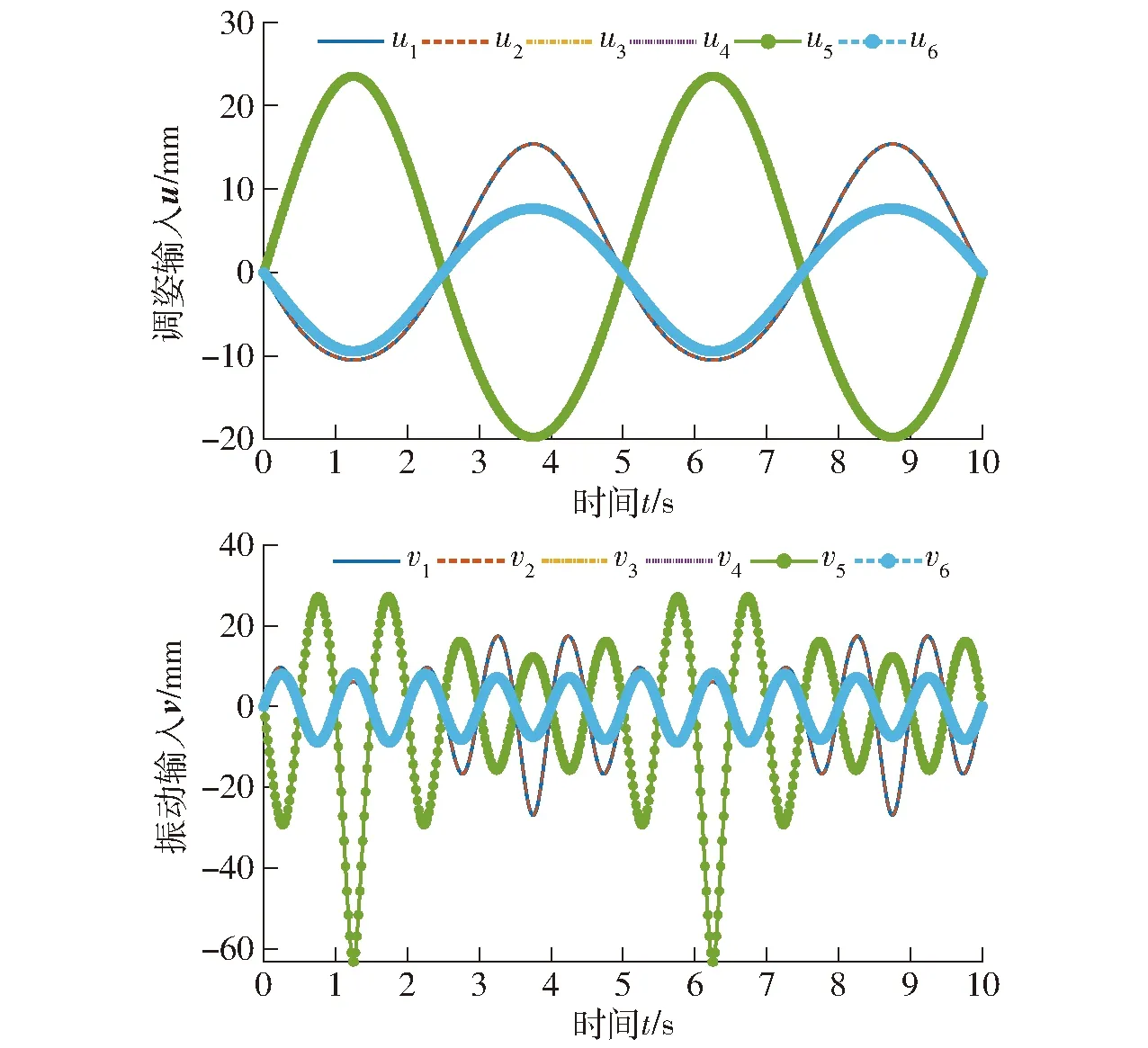
圖10 繞x軸轉動時雙輸入理論值Fig.10 Dual-input theoretical value of x-axis rotation

繞x軸轉動時，容易判斷分支1、2，分支3、6和分支4、5的驅動規律兩兩相同，因此圖10中6條分支的驅動曲線兩兩覆蓋，呈現3種規律。雙模融合機構的運動學仿真需要通過2次仿真來驗證。第1次，設定動平臺運動規律為r1x(t)，并且令v(t)=0，仿真后測量u(t)的變化規律；第2次，設定動平臺運動為r(t)，并將上一次仿真所得數據u(t)作為已知條件給入系統，仿真后測量v(t)。兩次仿真得到的輸入增量u(t)和v(t)的變化曲線如圖11所示。

圖11 繞x軸轉動時雙輸入仿真值Fig.11 Dual-input simulation value of x-axis rotation

對比圖10和圖11可知，理論計算值與仿真值的變化趨勢一致。進一步精確對比，將仿真數據導出并與每一時刻的理論計算值作差，得雙輸入偏差曲線，如圖12所示。

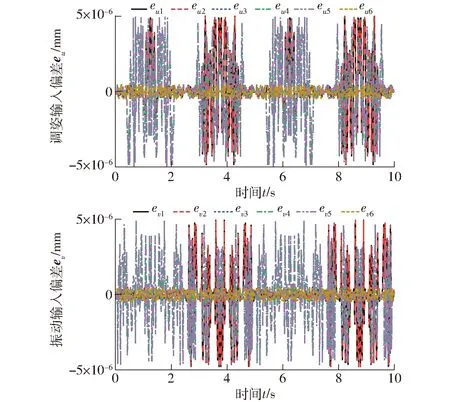
圖12 繞x軸轉動時理論與仿真輸入偏差Fig.12 Input deviation between theory and simulation of x-axis rotation

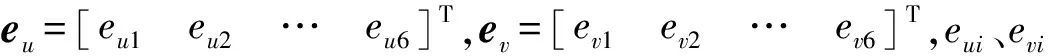
(2)繞y軸方向轉動

給定繞y軸轉動的雙模融合運動規律為

(25)

其中

ry(t)=r1y(t)+r2y(t)

(26)

式中ry——y軸角位移

r1y——y軸角位移位姿運動分量

r2y——y軸角位移振動分r1y(t)=8°sin(2πt/3)，r2y(t)=0.5°sin(4πt)。同樣按先Wu(t)后Wv(t)計算u(t)和v(t)的理論值，如圖13所示。

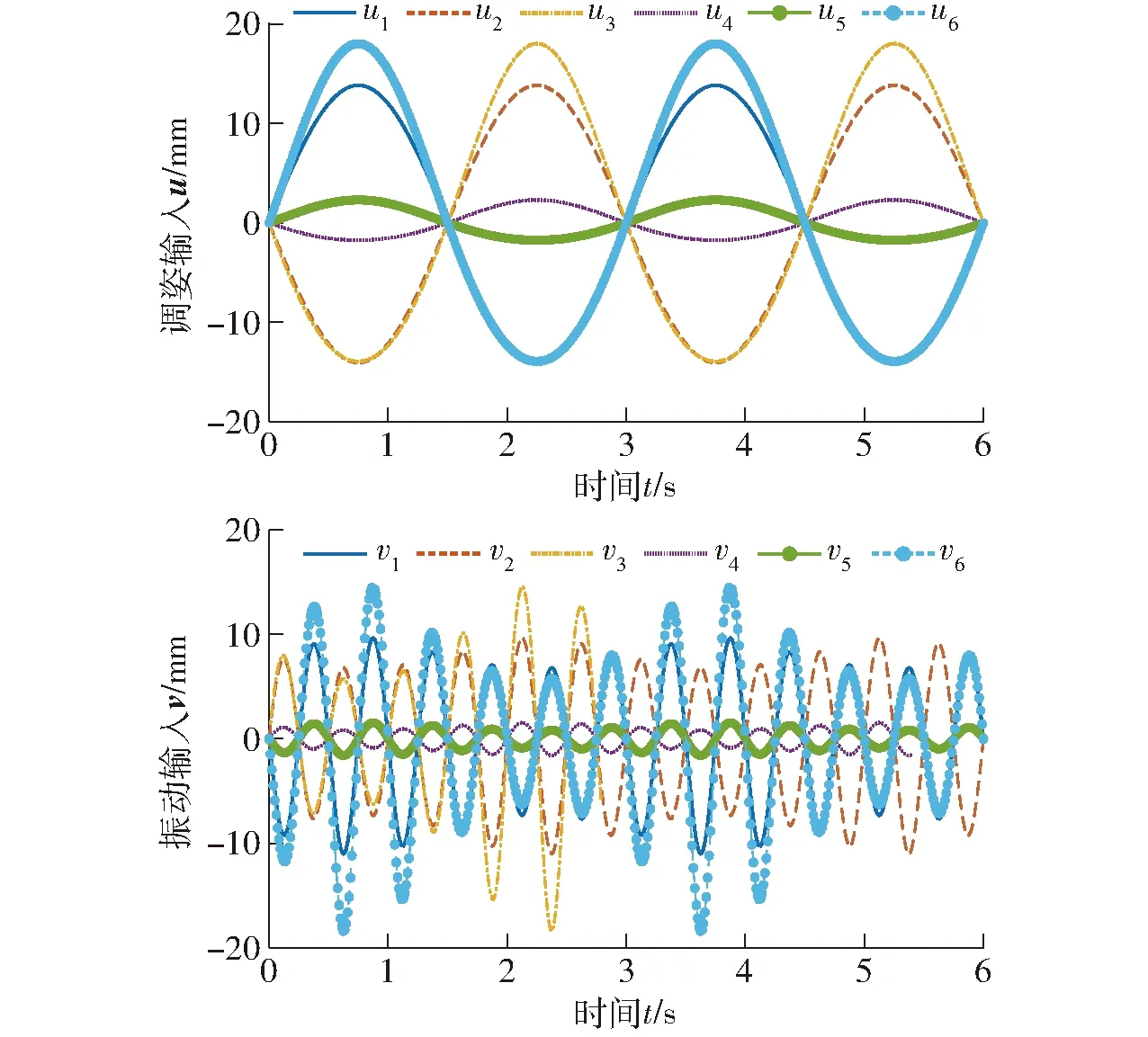
圖13 繞y軸轉動時雙輸入理論值Fig.13 Dual-input theoretical value of y-axis rotation

以相同運動規律在ADAMS中仿真，仿真同樣需要兩次，得仿真結果如圖14所示。

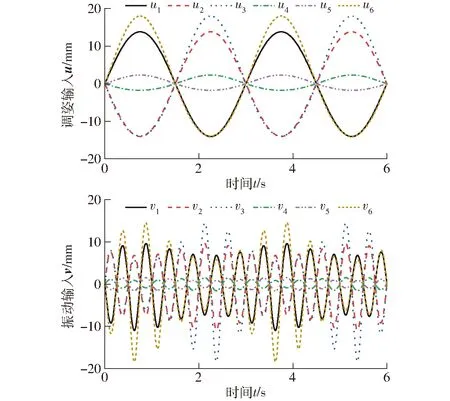
圖14 繞y軸轉動時雙輸入仿真值Fig.14 Dual-input simulation value of y-axis rotation

對比圖13、14可知，理論計算與仿真結果曲線變化規律基本一致。進一步精確驗證，同樣作出理論計算與仿真結果的偏差曲線如圖15所示。

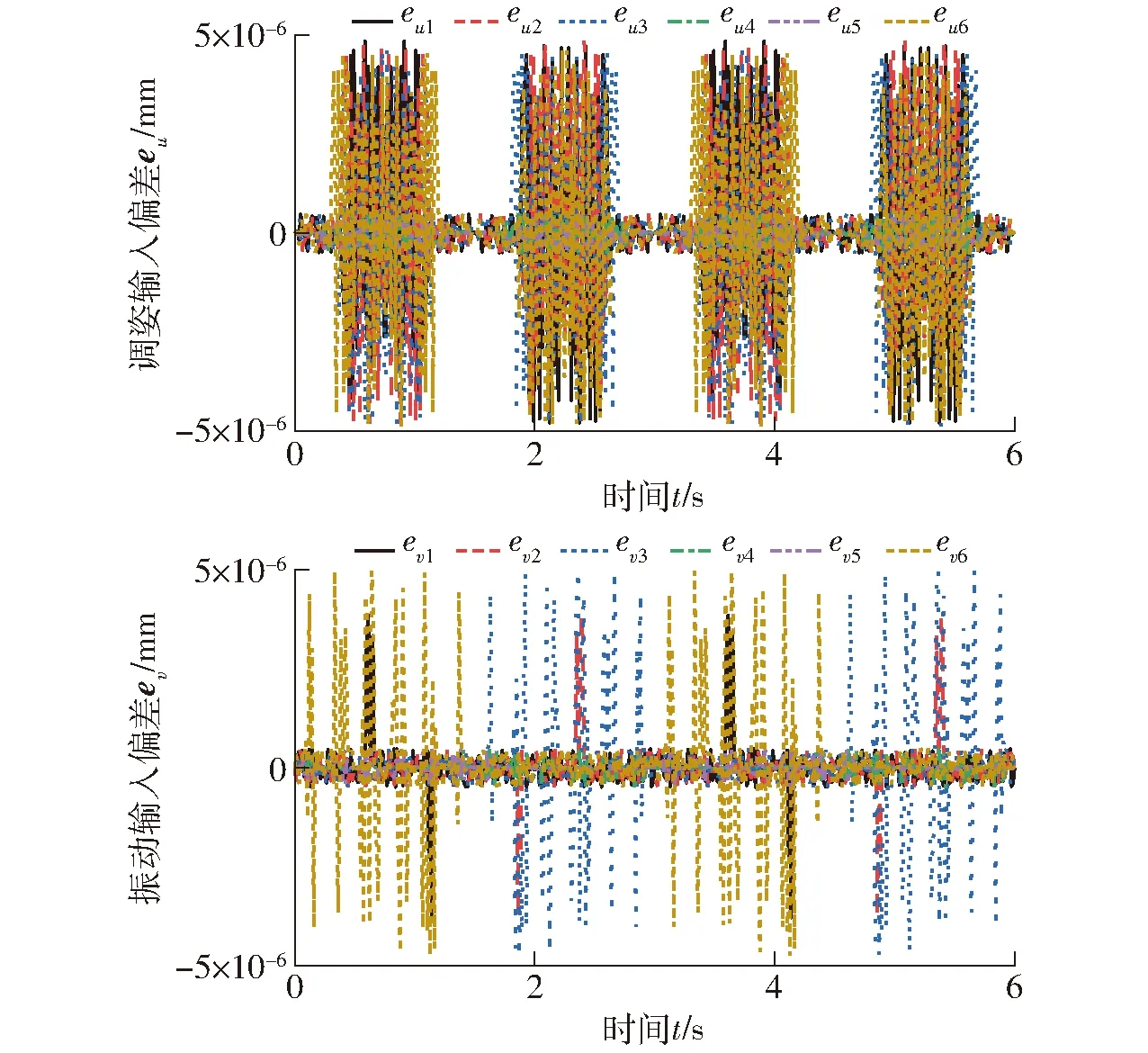
圖15 繞y軸轉動時理論與仿真輸入偏差Fig.15 Input deviation between theory and simulation of y-axis rotation

圖15中偏差數據同樣為10-6量級，再次證明機構輸出單自由度的融合運動時，理論值與仿真值完全一致。通過以上兩個算例可以證明，機構反解的理論模型對于單自由度運動是正確的。

5.3 多自由度運動融合算例

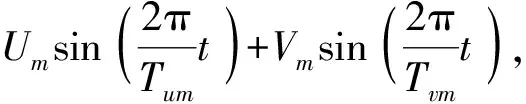
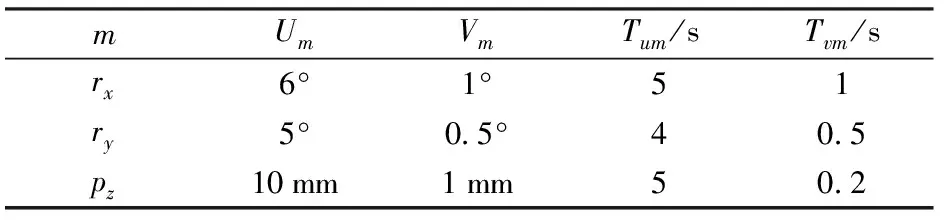
表2 融合運動參數Tab.2 Fusion motion parameters

圖16 三軸復合下雙模融合運動輸入理論值Fig.16 Theoretical values of inputs with dual-mode fusion motion under triaxial composite

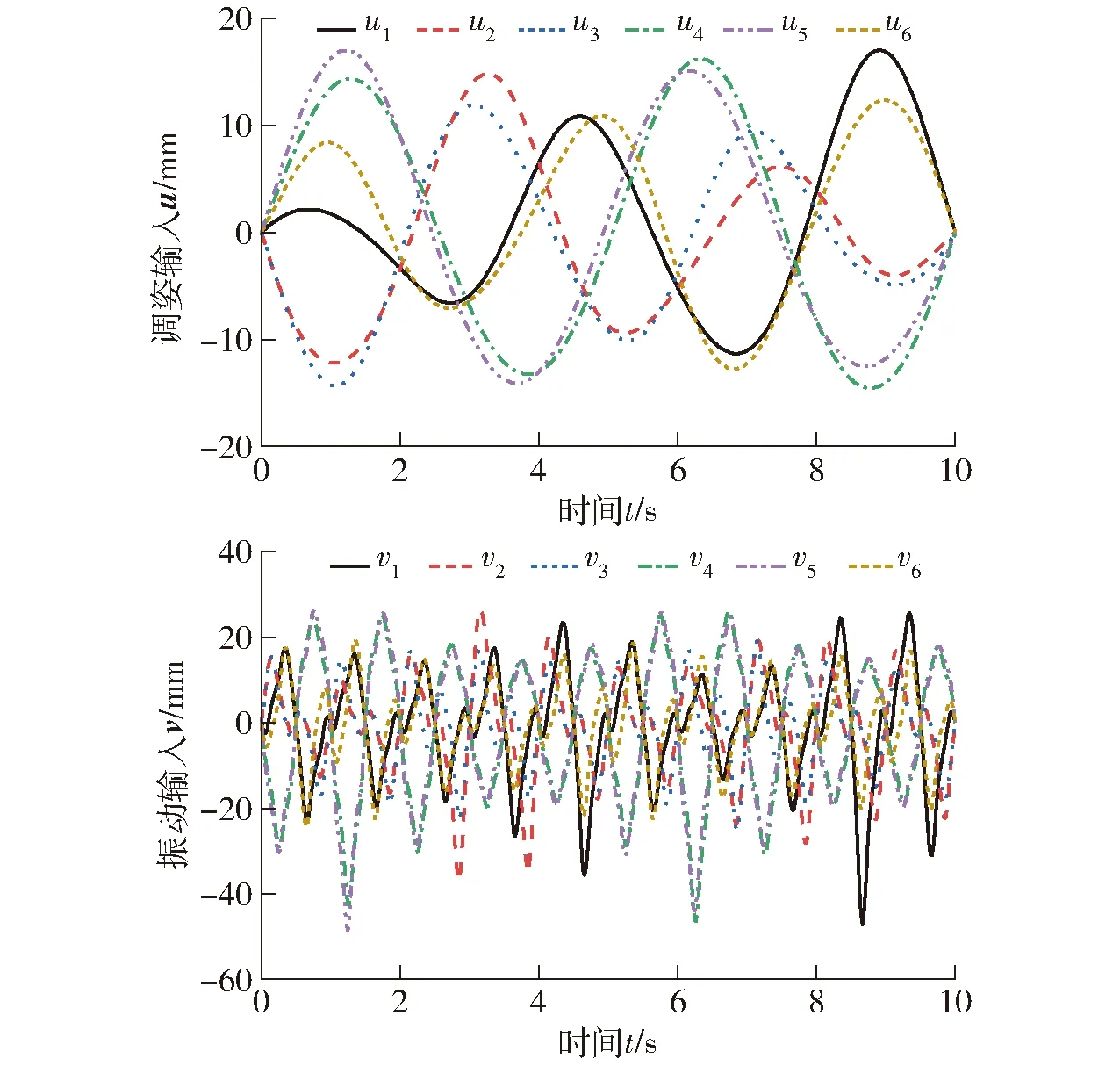
圖17 三軸復合下雙模融合運動輸入仿真值Fig.17 Simulation values of inputs with dual-mode fusion motion under triaxial composite

根據給定的運動規律，并按先Wu(t)后Wv(t)規則，通過理論模型計算得雙輸入曲線如圖16所示。以同樣的運動規律和求解規則，運用ADAMS仿真得輸入曲線如圖17所示。計算、仿真過程與單自由度算例相似。

對比圖16、17可知，三軸復合下，平臺進行雙模融合運動，輸入理論計算值與仿真值變化趨勢一致。導出理論值與仿真值數據，兩者作差，并繪制偏差曲線如圖18所示。

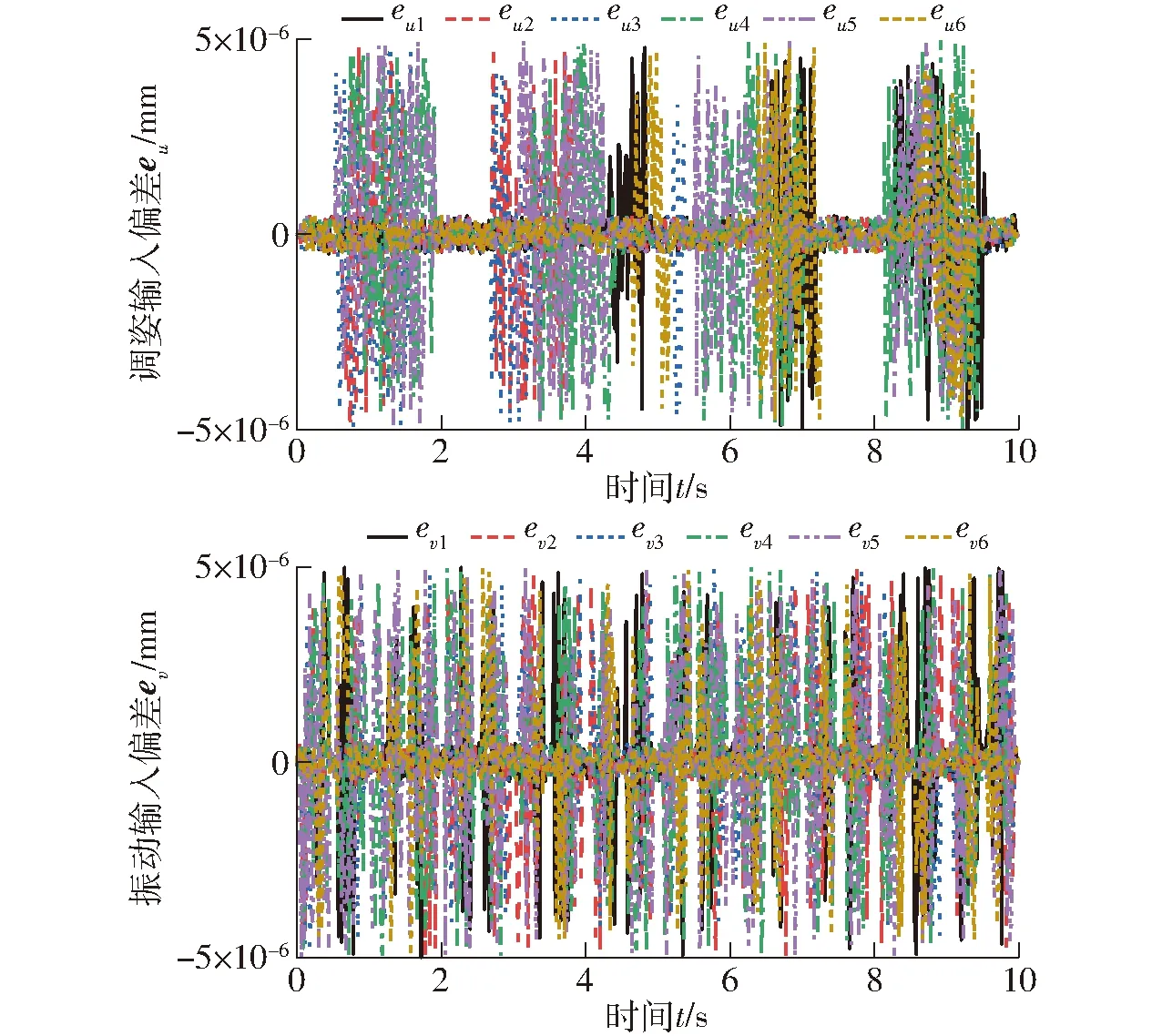
圖18 三軸復合下雙模融合運動輸入偏差Fig.18 Input deviationof dual-mode fusion motion under triaxial composite

由圖18可知，任意時刻理論計算與仿真結果的偏差均在10-6量級，可以認定理論結果與仿真結果完全相同。證明運動學反解理論模型對于多自由度復合下的雙模融合運動同樣正確。

5.4 運動學正解算例與仿真

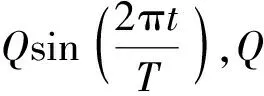
根據上述關系，任意給定一組各輸入的幅值和周期，參數如表3、4所示。

表3 調姿輸入參數Tab.3 Attitude adjustment input parameters

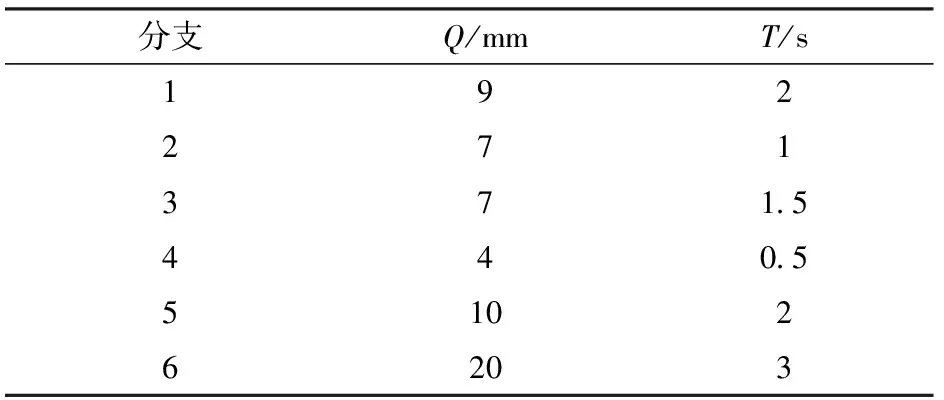
表4 振動輸入參數Tab.4 Vibration input parameters

根據運動學正解的理論運算流程，在雙輸入融合驅動下，動平臺的6維位姿輸出曲線如圖19所示，其中，rx、ry、rz為按x-y-z順序歐拉角測量，rz為z軸角位移；px和py分別表示x軸位移和y軸位移。并將同樣的驅動規律給入仿真模型，仿真后測量動平臺的位姿輸出，方位度量規則以及位置測量參考點與理論計算保持一致，測量結果如圖20所示。

從圖19、20可以看出，每個自由度上的運動均呈現大幅值上疊加小幅值的規律，證明機構能夠把雙輸入子閉環內的兩個獨立的輸入進行融合，并在輸出運動上得以體現。對比理論結果和仿真結果，可以看出，動平臺輸出運動的規律是一致的。進一步精確對比，將仿真結果導出，并與理論計算值作差，得到正解位姿輸出的偏差曲線如圖21所示。

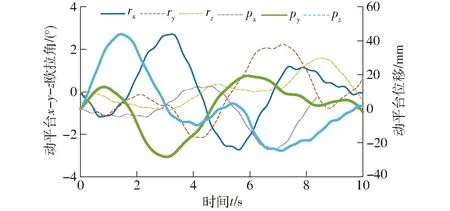
圖19 動平臺位姿理論值Fig.19 Theoretical posture of moving platform

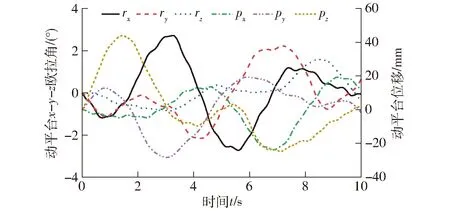
圖20 動平臺位姿仿真值Fig.20 Simulation posture of moving platform

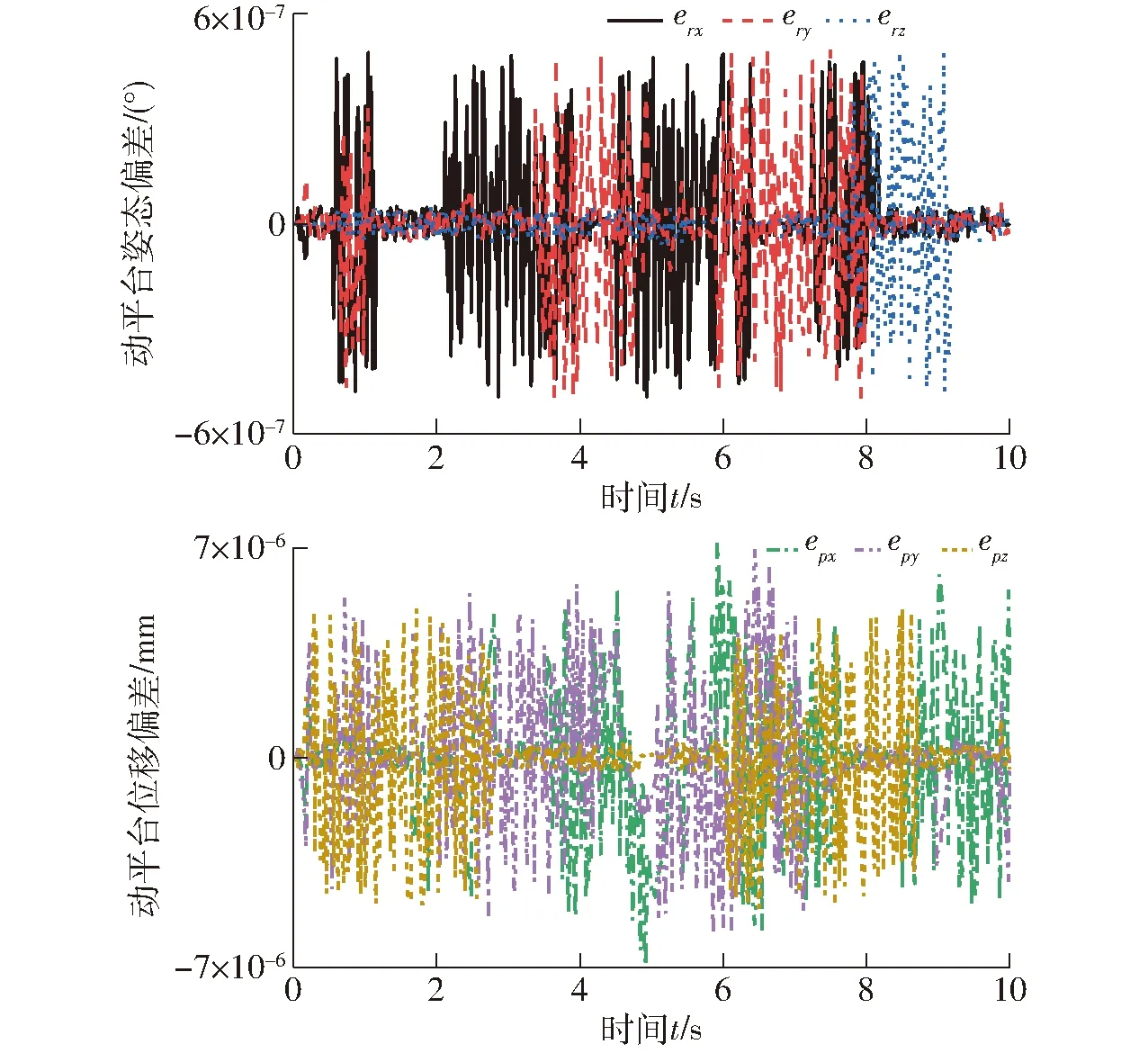
圖21 理論值與仿真值位姿偏差Fig.21 Deviation of posture between theory and simulation

圖21中，erx、ery、erz分別表示歐拉角3個方向的偏差，epx、epy、epz表示3個方向位移的偏差。由圖21可知，偏差最大取值范圍仍在10-6量級，可以認定理論結果與仿真結果完全一致。證明機構正解的流程與方法同樣正確。

6 結論

(1)提出一種通過六桿機構與機構原驅動桿件組合的新型雙輸入子閉環結構。使機構既能實現雙模式運動融合，又可以保持原6-RUS機構的原動件不變。

(2)建立機構運動學反解模型和內、外層機構數值方法的正解流程，將分析過程分為子閉環內與外主體機構兩部分，子閉環的輸出運動即為外主體機構的輸入，其中外主體即為6-RUS機構，可以直接運用原有結論進行分析，將雙輸入融合的難點問題集中在雙輸入子閉環內。

(3)通過算例分別對單軸運動雙模融合、多軸復合運動雙模融合的反解，以及雙輸入融合驅動下的正向運動學進行理論計算與仿真驗證，結果表明，理論分析結果與仿真結果完全一致，證明了針對所提構型所建立的運動學分析模型以及計算流程的正確性。