基于PIV試驗示蹤粒子添加方式的研究

邱奕龍 陳薈宇 曾鴻基 吉雷

1.中國石油西南油氣田公司天然氣研究院 2.中國石油天然氣集團公司天然氣質量控制和能量計量重點實驗室 3.西華大學流體及動力機械教育部重點實驗室

隨著計算機和處理圖像技術的飛速發展，利用集流動可視化和流動測試一體的PIV(Particle Image Velocimetry)技術成為了研究流場特性的新興方向[1-2]。

PIV技術為一種利用彌散在流體中的粒子對光的散射作用，用光學方法測得粒子在流場中不同時刻的位移，并基于粒子的跟隨性來確定流場的各種參數的技術[3]，相比于其他測試流場的方式，大大降低了對流場本身的擾動。倪銳等[4]利用PIV技術對天然氣管道內流場進行測量，發現PIV技術測量誤差很小，符合實際要求。而加注示蹤粒子是PIV測量的前提條件，示蹤粒子的添加方式對流態擾動有不同影響，內部示蹤粒子分布也不盡相同。馬昌友等[5]通過PIV對暫沖式風洞高亞音速平面葉柵流場進行測量時發現了示蹤粒子越大對流動的跟隨性越差；陳瑩等[6]在低速風洞中完成了對PIV示蹤粒子最佳投放位置的研究。應用PIV技術測量流場時，示蹤粒子加注方式對流場和示蹤粒子質量濃度的分布存在影響，對示蹤粒子加注方式的研究十分必要。

為了更加深入地探索示蹤粒子的加注方式對流場及質量濃度分布的影響，設計了3種示蹤粒子加注方式，并比較對流場的擾動情況和粒子的分布規律，得到最優加注方式，為PIV測量技術提供理論指導。

1 理論

流體在流動過程中遵循連續性方程和動量方程。

連續性方程即流入控制體內的凈質量流量與控制體內由于密度變化在單位時間里所增加的質量相等[7]，連續性方程的理論公式如式(1)所示[8]。

(1)

式中：ρ為氣體密度，kg/m3；t為時間，s；u、v、w分別為流體沿x、y、z3個方向的速度，m/s。

動量方程即一個系統不受外力或所受外力之和為零[8]，這個系統的總動量保持不變，理論公式如式(2)～式(4)所示[9]。

(2)

(3)

(4)

式中：P為流體所受壓力，Pa。

本次模擬采用的顆粒模型為液滴，粒徑為1×10-6m，質量流量為1×10-20kg/s。由于在實際試驗過程中，顆粒將會受到流場中的拖曳力、浮力、壓力梯度力和虛擬質量力，其顆粒在拉格朗日坐標系下所受到的力學平衡方程如式(5)～式(8)所示[10]。

(5)

(6)

(7)

(8)

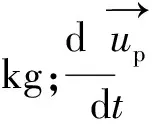
2 數值模型

2.1 幾何模型

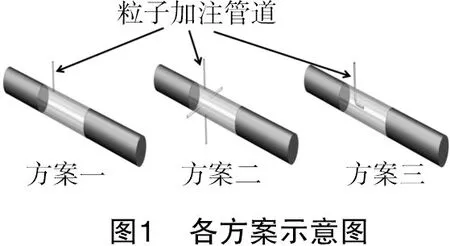
本次數值模擬使用NX10.0軟件對幾何模型進行繪制，天然氣主管流道為直徑100 mm、長度5 000 mm的圓柱形流道，采用3種方案對示蹤粒子進行加注，加注位置均為距主管流道入口800 mm處。方案一為單旁通管道加注粒子；方案二為四旁通管道加注粒子；方案三為L型管道加注粒子。各方案模型示意圖如圖1所示。

2.2 網格模型

對幾何模型進行網格劃分是所有CFD的基礎，網格劃分的意義在于將連續的流體利用網格塊離散化[10]。本次數值模擬對3個方案的模型進行了網格劃分，并對其進行了網格無關性驗證，當網格數量為3 282 718時，所有方案的監測點物理量均不隨網格數增加而改變，本研究的所有模型的網格數量均大于3 282 718。

2.3 計算模型

采用FLUENT進行數值模擬，湍流模型standardK-ε，近壁面函數選擇Standard Wall Functions，流體介質為甲烷，主管道入口采用速度入口，流量為100～600 m3/h，出口為壓力出口，壁面采用光滑無滑移壁面。壓力速度耦合采用SIMPLEC算法，空間離散模型除了Gradient采用最小二乘法，其余均為二階迎風格式。選擇液滴作為示蹤粒子，粒徑為e-6m，為了更加貼合真實粒子加入管道中，在DPM模型中采用粒子與流場耦合的方式求解粒子顆粒的軌跡，并假設粒子在流場中受到剪切力、壓力梯度力和虛擬質量力。

3 結果分析

3.1 不同添加方式對流場湍流強度的影響分析

湍流強度是表征流場微觀脈動特征的重要參數之一，它是速度波動的均方根與平均速度的比值，在探究管道內流場的流動特性時，需要著重關注流場內的湍流強度，當湍流強度小時，流場即趨于穩定[11]。

湍流強度計算公式如式(9)所示。

(9)

式中:I為湍流強度，無因次。

本次數值模擬應用上述數值模型，應用 FLUENT軟件，對3種方案在各個進口流量下的流場內湍流強度進行了計算，繪制了不同方案對流場湍流強度影響的單線圖(見圖2)。

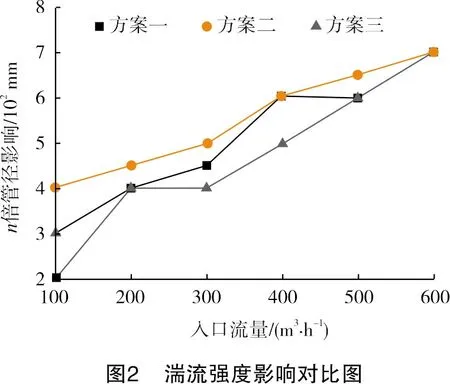
如圖2所示，在大流量600 m3/h 時，3種方案對流場湍流強度的影響均在7倍管徑以內，小流量100 m3/h時，方案一對流場湍流強度的影響最小，而當流量大于200 m3/h 后，方案二對流場湍流強度的影響略大于方案一、方案三。

這是由于單管加注相比多管加注時，示蹤粒子僅從一個方向進入，減少了對流場截面上流體整體的擾動，而相比于L型管的加注方式，單旁通管并未過多地伸入流場內部，所以其擾動也小于L型管加注方式。而當入口流量開始較大時，這些影響開始變得可以忽略，所以方案一優于方案二、方案三。

3.2 不同添加方式對流場渦量的影響分析

旋渦是流體中非常常見的一種運動形態，渦量是描寫旋渦運動的物理量，為流體速度矢量的旋度[12-13]。渦量動力學方程是反映旋渦流體變化規律的方程,如式(10)所示[14]。利用該方程可說明流體中旋渦的產生、變化現象，且渦量越小時，流場越穩定。

(10)

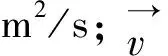
使渦量發生變化的因素有質量力、壓強梯度、黏性應力、流體壓縮或膨脹、渦線變化等[15]，本次試驗中3種示蹤粒子的加注方式必然對原流場產生擾動影響。為此，應用FLUENT軟件，對3種方案在各個進口流量下的流場內渦量分布進行了計算(見圖3)。

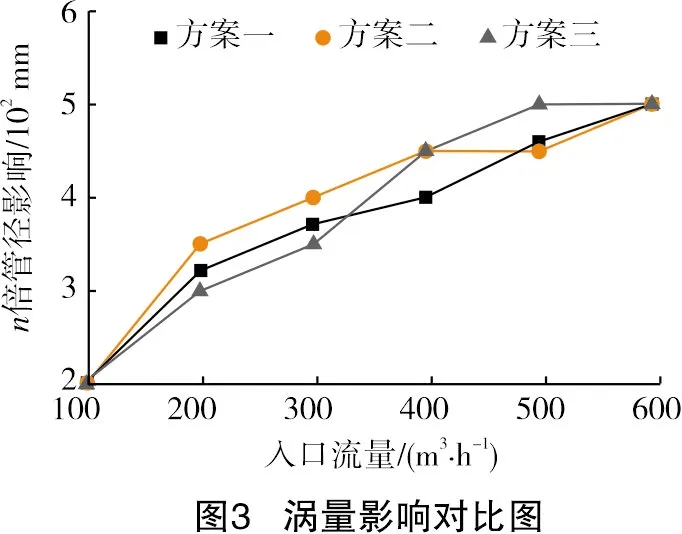
由圖3可以看出，3種方案在各種流量下對流場渦量的影響均在5倍管徑以內。當流量在300 m3/h以下時，方案三對流場的渦流影響小于方案一、方案二，這是因為方案三的示蹤粒子是順著流場流動的方向而釋放出的，所以示蹤粒子與天然氣的流動方向從一開始就相同，這就使得流場的渦量變化沒有方案一、方案二那么大。而當流量大于300 m3/h后，由于L管的管壁直接伸入到管道內部，流量大時對管壁的擊打程度大，此時方案三對流場渦流的擾動略大于方案一、方案二。

3.3 不同添加方式粒子質量濃度分布情況的分析

PIV技術是通過采集管道內示蹤粒子在CCD相機兩次曝光的位置，利用位置差除以曝光時間求得速度，進而求得和速度有關的其余物理量[16]。因此，要得到完成的流場結果，其示蹤粒子在管道內的分布必須均勻，為此，對不同添加方式的示蹤粒子質量濃度分布進行了對比。

圖4為不同加注粒子方式的質量濃度分布圖。由圖4可知，方案二的示蹤粒子分布最好，各處較為均勻，方案一次之，方案三的粒子幾乎全部分布于管道中部。造成這一現象的原因是方案一和方案二的示蹤粒子在加注時存在與主流場速度方向垂直的速度，且粒子在y方向行駛的過程中，直到主管底部粒子y方向速度仍不為0，故顆粒在流場的剪切力作用下，會布滿整個管道；方案三的示蹤粒子分布主要集中在管道中心位置，管壁附近顆粒質量濃度較低。這是由于L型管道的粒子出口y方向速度很小，且主管道的流速也較小，湍流強度不高，以至于顆粒無法到達管壁附近，造成粒子分布不均的現象。

由圖4可以看出，方案二的粒子分布最好，各處較為均勻，方案一次之，方案三的粒子幾乎全部分布于管道中部。由于方案一和方案二的示蹤粒子在注射時存在與主流場速度方向垂直的速度，且粒子在y方向行駛的過程中，直到主管底部粒子y方向速度仍不為0，故顆粒在流場的剪切力作用下，會布滿整個管道；方案三的示蹤粒子分布主要集中在管道中心位置，管壁附近顆粒質量濃度較低。這是由于L型管道的粒子出口y方向速度很小，且主管道的流速也較小，湍流強度不高，以至于顆粒無法到達管壁附近，造成粒子分布不均的現象。

3.4 試驗

為驗證數值計算的準確性，對四管加注示蹤粒子的方式進行了試驗，試驗在國家石油天然氣大流量計量站成都分站和西華大學流體與動力機械教育部重點實驗室進行。實際試驗過程中，采用PIV設備對天然氣管道示蹤粒子添加方式進行了研究，實驗設備見圖5～圖6。

試驗中將透明管設置在距加注口10倍管徑(10d)處，通過粒子成像測速儀進行測試，由PIV高速CCD相機獲取粒子速度矢量圖，試驗壓力1.5 MPa，試驗溫度31 ℃。從兩個流量工況來看，天然氣流速矢量箭頭方向一致，沒有明顯漩渦，表明此處流體流動平穩，上游示蹤粒子加注對下游流態的影響已基本消弭；整個測量區域均存在粒子速度矢量，說明示蹤粒子分布可布滿管道。該結果與數值計算結果相符，證明了此次數值模擬的可靠性。圖7所示為PIV測試結果。

4 結論

(1)單管加注示蹤粒子在小流量下對流場的影響較小，隨著流量的增大，對流場的影響程度增大；多管加注示蹤粒子在大流量時對流場影響與單管加注差異不大；L管加注示蹤粒子在各流量下對流場的影響均較小。

(2)L型管道加注示蹤粒子時，粒子在管道內的分布極不均勻，幾乎全部集中于管道中部，所以不宜用于PIV測量，容易造成誤差，而多旁通管道注射示蹤粒子后粒子在管道流場內的分布最為均勻。

(3)通過PIV裝置對四管加注示蹤粒子的方式進行了驗證，試驗結果顯示，天然氣流速矢量箭頭方向一致，沒有明顯旋渦，表明流體流動平穩，上游示蹤粒子加注對下游流態的影響已基本消弭；整個測量區域均存在粒子速度矢量，表明示蹤粒子分布可布滿管道。該結果與數值計算結果相符，證明數值模擬的可靠性。

綜上，多旁通管道注射示蹤粒子為天然氣管道內流場最優示蹤粒子加注方案。