山竹臺風的非平穩風特性研究

段 靜， 張 麗， 謝壯寧， 劉慕廣

(1.華南理工大學 亞熱帶建筑科學國家重點實驗室,廣州 510641；2.深圳市國家氣候觀象臺，廣東 深圳 518040)

臺風登陸過程城市地區高空風場特性是超高層建筑抗風設計最為關注的重要基礎性問題，現場實測是獲取臺風特性的最可靠方法[1-2]。常見的近地風場觀測主要依托地表附近的氣象觀測站、近年因風能資源研究所設置的高度百米以內的氣象觀測塔、風廓線儀等。在結構抗風研究中，為了獲取高空臺風湍流的特征，沿海城市的超高層建筑物頂部安裝的風速儀則成為獲取臺風實測數據的主要來源[3-5]。出于安全方面的考慮，這些風速儀大多會安裝在略高于屋面處，較難消除建筑本身的干擾影響，從而難以真正獲取高空自由風場的風速數據。因而具備一定高度的氣象塔獲取的實測資料對高空臺風描述則彌足珍貴。

良態風場的實測風速序列按照平穩隨機過程處理是共識，而臺風風場的實測風速序列則具有明顯的非平穩特征。對于非平穩隨機過程的描述主要有兩類方法：①Gramer分解理論指出任意一個時間序列分解為時變確定性趨勢成分和平穩零均值隨機成分，把非平穩風速視為時變平均風速和平穩脈動風速的疊加[6]；②Priestly[7]提出的演變譜方法將非平穩過程表達成某個平穩過程與一確定性的調制函數的Fourier-Stieltjes積分，把非平穩風速視為時變平均風速和非平穩脈動風速的疊加。

臺風風場的非平穩性分析中時變平均風速的提取是關鍵。早期的最小二乘擬合法、短時平均法等，后期因其自適應性而得到廣泛應用的經驗模態分解(empirical mode decomposition,EMD)和離散小波變換(discrete wavelet transform,DWT)都曾用于提取時變趨勢項。例如：Xu等[8-11]最先基于EMD的方法，提取非平穩風速序列中的時變平均風速。申建紅等[12]對比了EMD和DWT提取時變均風的精度，認為小波變換的方法更為準確可靠。吳本剛等[13-14]基于EMD的方法對超高層結構西塔頂部445 m高度的實測數據和利通廣場303 m高度的實測數據進行非平穩分析,拓展了時變的物理量，驗證了非平穩風速模型的準確性和優越性。安毅等[15]對臺風作用下上海環球金融中心492 m高度處的實測風速序列采用EMD方法進行了高空風場分析。已有的這些工作針對非平穩臺風風場的研究均是將脈動風速視為零均值平穩風速，按照平穩隨機理論分析湍流特性；對于時變趨勢項，不同文獻均采用不同的提取方法，這些方法對風場特性參量分析結果的影響尚未進行全面的對比研究。

若研究非平穩脈動風速的時變湍流特性則需結合演變譜估計方法，常用譜估計方法包括短時傅里葉變換(short-time Fourier transform,STFT)，小波變換或者S變換等，其應用的難點在于調制函數和目標譜的確定。Huang等[16]通過改進時變功率譜密度的估計方法，對非平穩臺風的時變功率譜，時變相干函數等進行研究，指出時變Karman譜和Krenk相干函數模型適合描述非平穩臺風的頻域特性。Wang等[17]依托蘇通大橋橋址區風速記錄探討非平穩臺風的時頻特性，使用不同小波方法去估計時變功率譜，發現其結果和時變Kaimal譜相比差別較大。

本文根據2018年超強臺風山竹發展期間深圳氣象梯度觀測塔(SZMGT，塔高356 m)所完整記錄的三維風速實測序列，結合風場非平穩性研究方法，對平均風速剖面、湍流強度、陣風因子、湍流積分尺度、脈動風速譜等風特性參量進行全面細致的分析，希望能夠加深對臺風作用下非平穩高空湍流特性的理解，同時擴充極端氣候下近地高空實測數據庫，為工程結構抗風設計提供借鑒。

1 觀測點、風況、分析內容及方法

1.1 觀測點概況

用于現場實測的深圳氣象梯度觀測塔(簡稱梯度塔)位于鐵崗水庫庫區如圖1所示，其周邊大范圍覆蓋著低矮叢林。該塔是目前國內唯一集邊界層氣象垂直探測、大氣環境監測、雷電防御科學研究、氣象災害實景監視于一體的綜合觀測及試驗平臺，能實現從地面到城市冠層對臺風等強天氣開展直接觀測，也是目前亞洲第一、世界第二高的桅桿結構鐵塔。利用該塔不同高度(分別位于離地10 m，40 m，160 m，320 m高度)安裝的三維超聲風速儀可有效測量不同高度處的時變風速，超聲風速儀采樣頻率為10 Hz。

1.2 風況及數據預處理

超強臺風山竹(編號201822)于北京時間9月7日在西北太平洋洋面生成，9月11日8時升至超強臺風級，9月15日2時以超強臺風級在菲律賓呂宋島東北部沿海登陸(登陸時中心附近最大風速為65 m/s)，9月16日17時從廣東臺山海晏鎮登陸(登陸中心附近最大風速為45 m/s)，沿西西北方向向內陸移動，并于9月17日17時停止記錄。根據深圳氣象臺的站點記錄結果，最大瞬時風速為48.7 m/s，最大10 min平均風速為40.7 m/s。圖2為深圳臺風網記錄的超強臺風山竹的路徑示意圖，圖中標注的是9月16日全天的氣候信息。臺風在移動過程中與深圳市最近距離大約120 km。

根據臺風持續時間和移動路徑，篩選出的數據分析樣本為9月16日00：00時—9月16日24:00時，共24 h的記錄數據。按照10 min基本時距劃分子樣本，由于存在4個梯度高度，24 h內共計144×4=576個子樣本，子樣本按順序依次編號。

強風過程伴隨的惡劣環境因素會影響測量數據的有效性，數據分析前需對原始數據進行預處理[18]，針對數據中的無效、個別缺失和奇點數據進行處理。在數據處理過程中發現320 m高度處14:00—17:00記錄時段以內有8個子樣本無效，分析時予以舍棄。

超聲風速儀記錄的三向瞬時實測風速序列記為ux(t),uy(t)和uz(t)。傳統矢量分解法對風速風向的轉換可參考吳本剛等進行。考慮臺風的風速和風向的時變特性時，矢量分解可參考以下公式進行

(1)

(2)

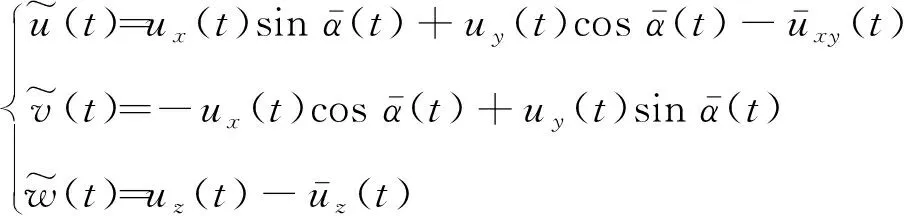
(3)

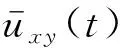
1.3 非平穩性研究方法

分析風速的非平穩特征時需先提取風速的時變趨勢，再進一步檢驗其非平穩特征。時變趨勢通常采用DWT或EMD方法。

采用DWT提取時變趨勢項時，首要考慮的是小波母函數選擇，核心問題在于分解層數的確定。小波母函數應選擇具有緊支集正交性的小波簇，例如db小波簇、coif小波簇、sym小波簇，本文采用精度較高的db10波；確定最佳分解層數時，先對信號進行最大分解層數分解，分別計算出各層小波能量，取小波能量突變層為最佳分解層數。本文利用最佳分解層數的低頻近似項經小波逆變化得到最優趨勢，作為信號的時變趨勢項。

考慮到EMD分解時可能出現的邊界效應和模態混疊問題，本文作了相應的處理。針對邊界效應問題,采用AR模型進行端點數據延拓,前后各自延拓20個數據點；針對模態混疊問題，采用了集合經驗模態分解(ensemble empirical mode decomposition,EEMD)，其中添加高斯白噪聲的標準差為0.01，添加噪聲的次數為50。將原始信號按照從高頻到低頻的方法分解成若干IMF分量，最后一項為殘差項，一般將殘差項和若干低頻項疊加即可認為是趨勢項。吳本剛等指出，殘差項疊加最后1～3項低頻項可大致認為是信號的時變趨勢項。本文通過分析認為殘差項疊加最后2項低頻項即可合理描述信號的時變趨勢。

提取趨勢項后的數據是否滿足平穩性，有很多的數學檢驗方法[19]，例如圖檢驗法，輪次檢驗法，逆序數檢驗法，單位根檢驗法等。綜合比較后，本文選擇逆序數檢驗方法對數據進行平穩性檢驗，其原理是將數據劃分多個子段，按順序形成子段的均值序列和方差序列，統計逆序(前面的數據大于后面的數據)的總數，構造統計量，并進行非參數假設檢驗，從而判斷數據的平穩性。

1.4 分析內容

對應于非平穩模型，相應要分析的主要脈動風場參量分別為湍流強度、陣風因子、湍流積分尺度和脈動風速功率譜。湍流強度定義為

(4)

式中:上標*表示非平穩模型;沒有上標*表示平穩模型的湍流強度(下同)。相應三個方向的陣風因子為

(5)

式中，tg為陣風風速的平均時距，一般取為3 s。湍流積分尺度根據脈動風速的自相關函數采用下式計算

(6)

式中,τ0.05為自相關系數降至0.05對應點[20]。用于對比的縱向脈動風速功率譜采用以下公式

(7)

2 結果分析

2.1 時變均值提取對比

為比較不同方法提取時變均值后的效果，對整個分析時長的水平方向瞬時總風速，采用平穩模型方法(SMM)、DWT和EEMD分別提取其時變均值的結果如圖3所示。 由圖3可見，三種方法提取的時變均值曲線和瞬時曲線的波動起伏趨勢一致，同時基于DWT或者EEMD方法的時變曲線基本圍繞SMM時變曲線上下波動。值得注意的是，圖3(d)中三種方法時變均值的缺失段涵蓋了缺失數據所處的子樣本整體長度。

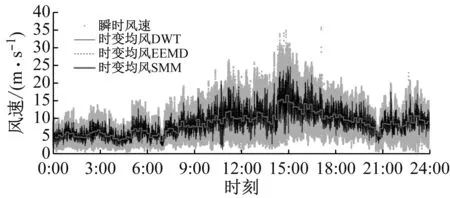
(a) 10 m

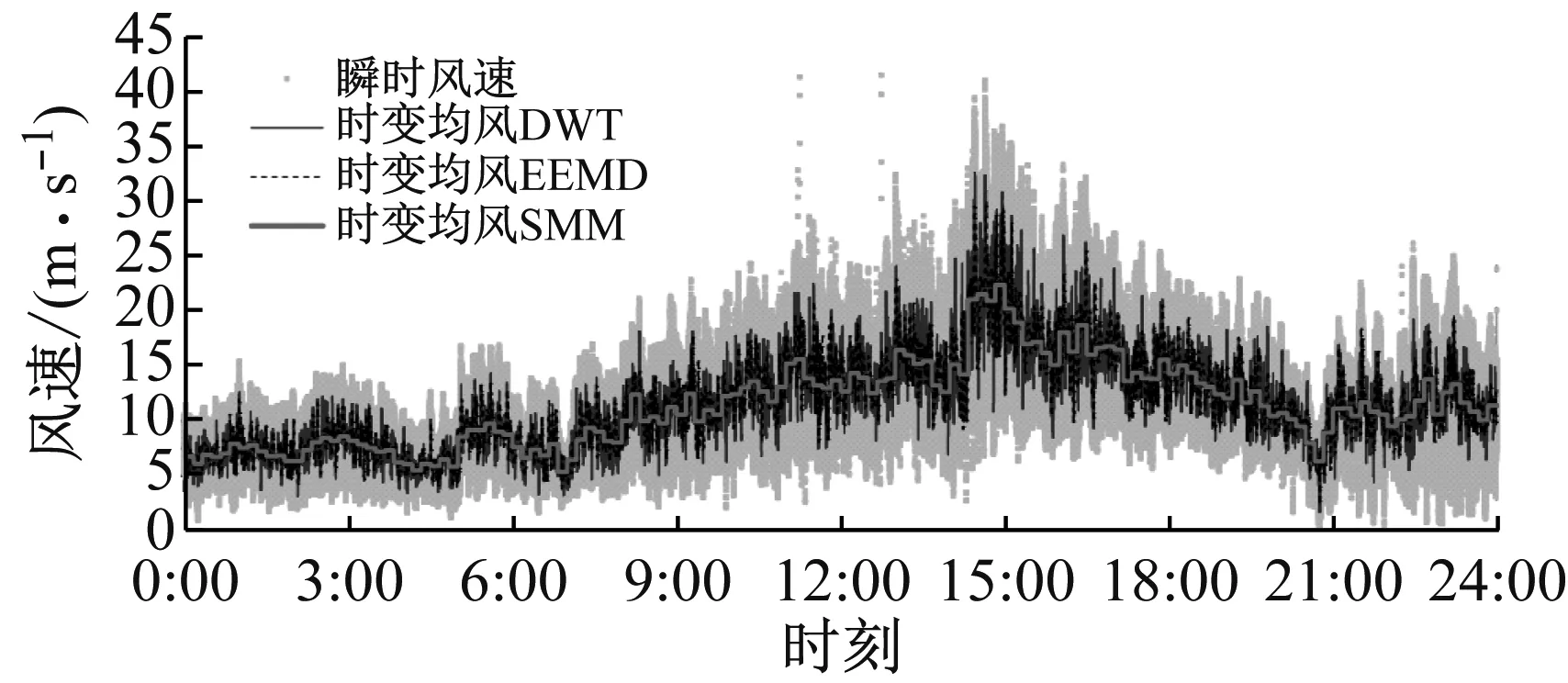
(b) 40 m

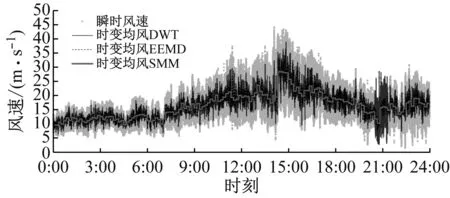
(c) 160 m

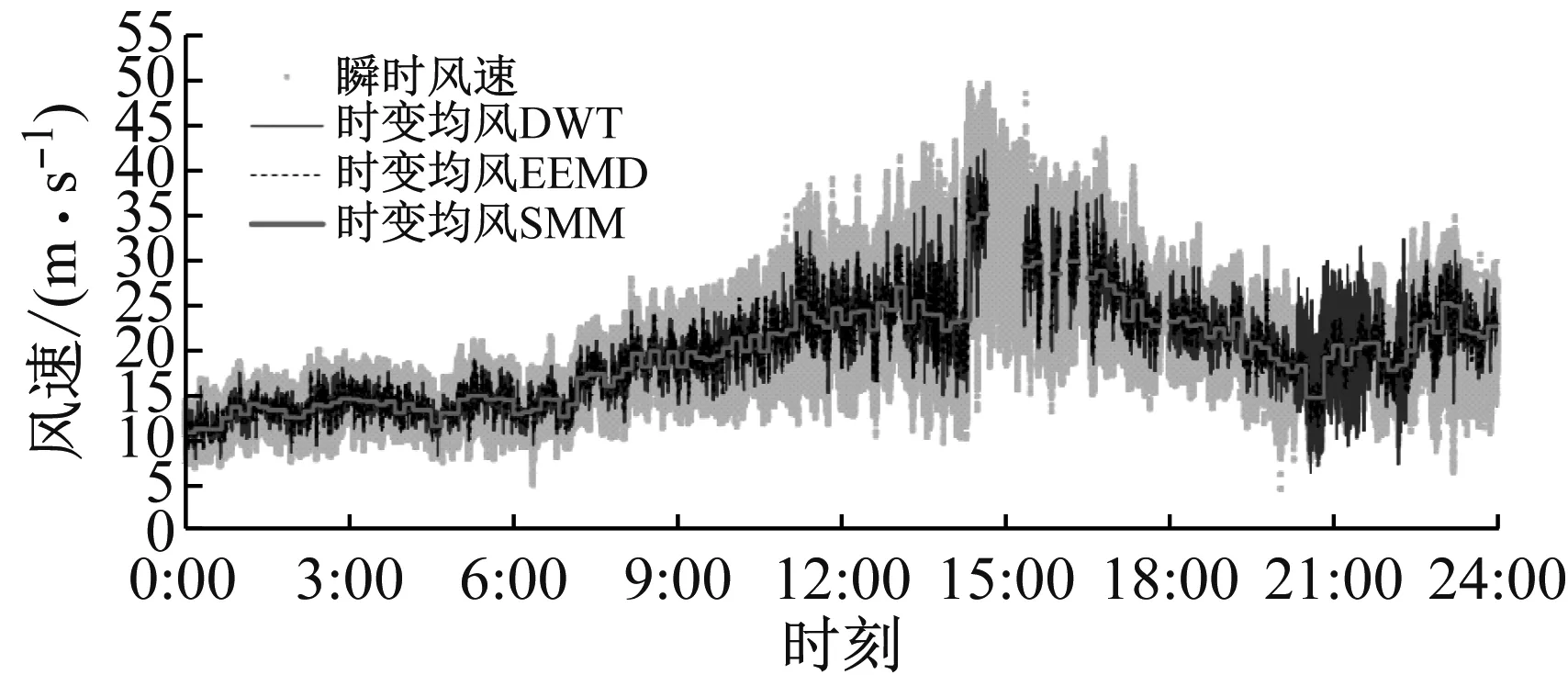
(d) 320 m圖3 時變均值對比Fig.3 Comparison of time-varying mean value

對水平方向的瞬時總風速提取時變均值后的剩余分量的方差進行分析。根據DWT的提取結果進一步計算10 m、40 m、160 m和320 m高度處的剩余分量方差分別為1.82、1.77、1.75和1.73，EEMD的相應結果為2.45、2.54、2.65和2.60，SMM的相應結果為2.65、2.79、2.90和2.89。對實測數據提取時變均值后，DWT對應的剩余分量的方差結果是最小的，所以申建紅等認為使用小波變換提取信號的時變趨勢項精度相對更高。

2.2 縱向平均風速剖面

取涵蓋最大風速時段(14:30—15:50)的臺風縱向平均風速剖面分析。基于各種方法繪制了該時段內10 min時距的子樣本平均風速剖面，并與現行GB50009—2012《建筑結構荷載規范》[21]建議的B類和C類地貌對應的風速剖面進行比較，結果如圖4所示。圖中DWT和EEMD 方法計算10min時距的平均風速時取相應時距內時變平均風速的均值。由圖4可見，大風時段梯度塔的實測平均風速剖面更接近C類地貌對應的風剖面(規范中對應地面粗糙指數取值0.22)。比較運用不同方法計算的同高度處的相對風速比值，SMM計算結果最大，EEMD方法次之，DWT方法最小。

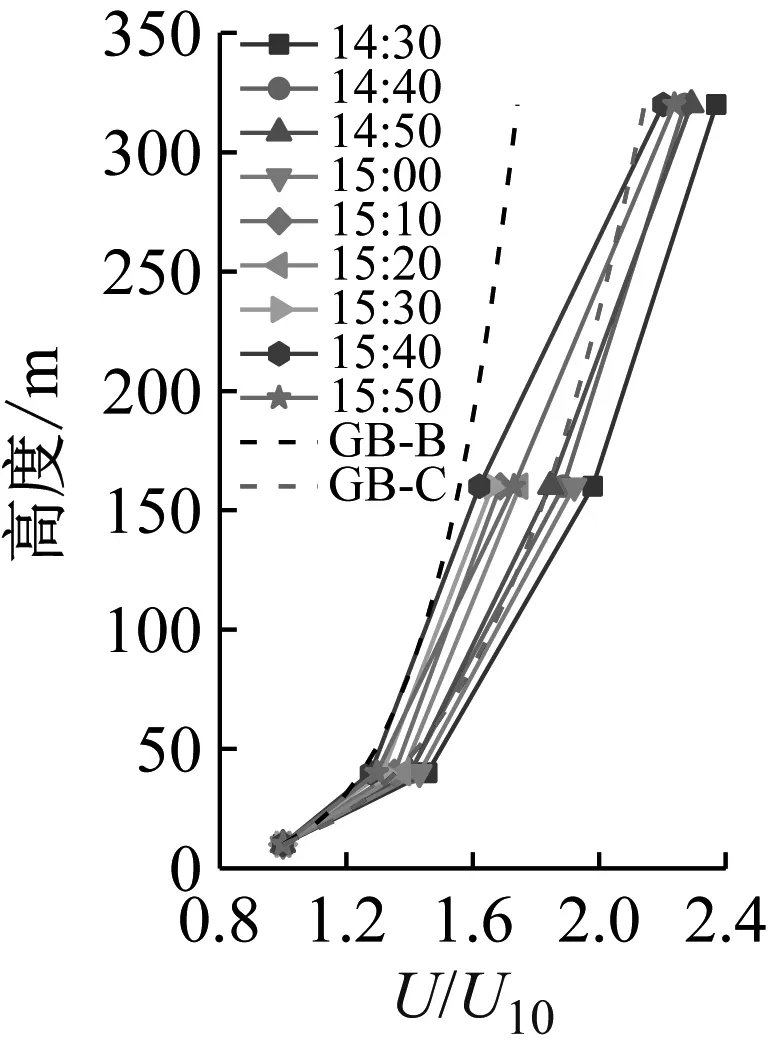
(a) SMM

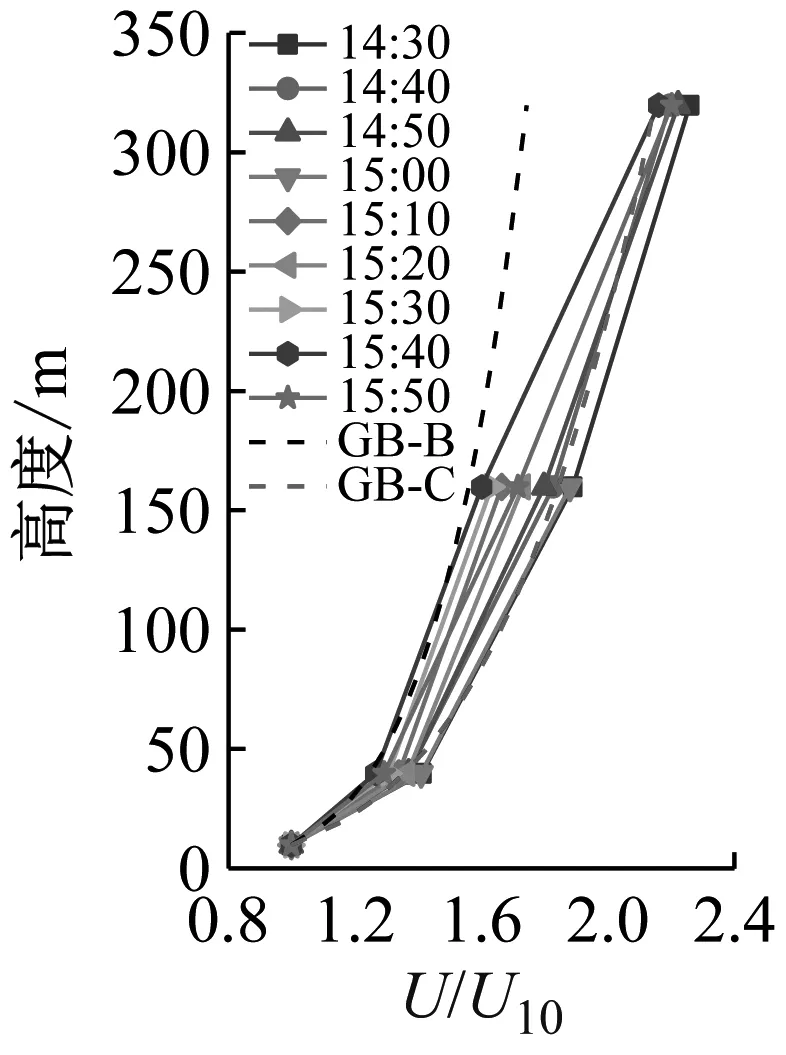
(b) DWT

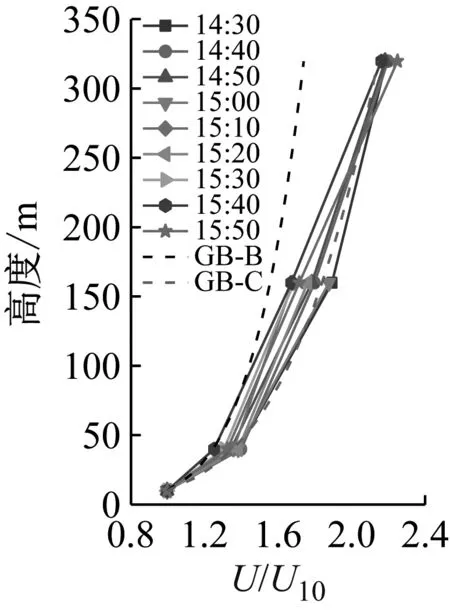
(c) EEMD圖4 平均風速剖面Fig.4 Mean wind speed profiles

2.3 樣本的平穩性檢驗結果

采用逆序檢驗法對基于各種方法分離的脈動風速的平穩性進行檢驗，結果如圖5所示。逆序檢驗方法中子段長度會對檢驗結果產生影響。本文取子段長度30(對應平均時距3 s)，對10 min子樣本的均值統計量進行假設檢驗。總體而言，采用DWT和EEMD后數據的平穩性優于SMM，說明提取時變趨勢項后，數據平穩性更好。當子段長度為30時，SMM中所有高度測點數據平穩性平均通過率為75.98%，而對應于DWT和EEMD方法的平均通過率分別為97.88%和97.08%。平穩性檢驗的結果為將脈動風速按照平穩隨機過程進行分析提供依據。

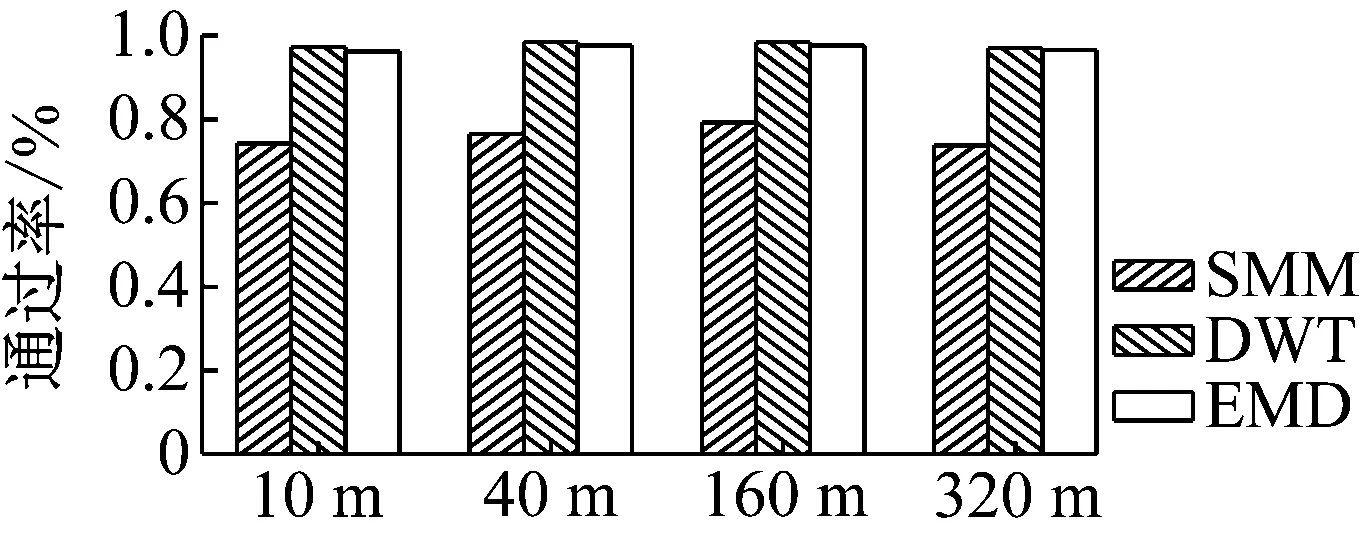
圖5 數據平穩性檢驗Fig.5 Data stationarity test

2.4 湍流強度

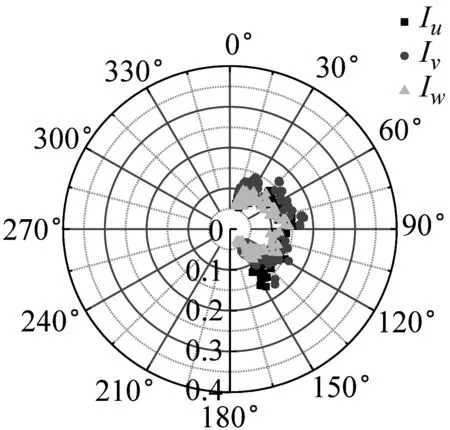
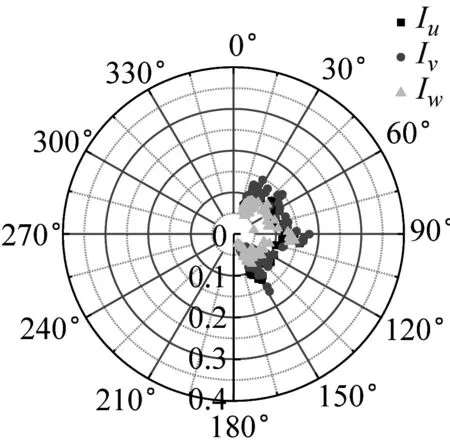
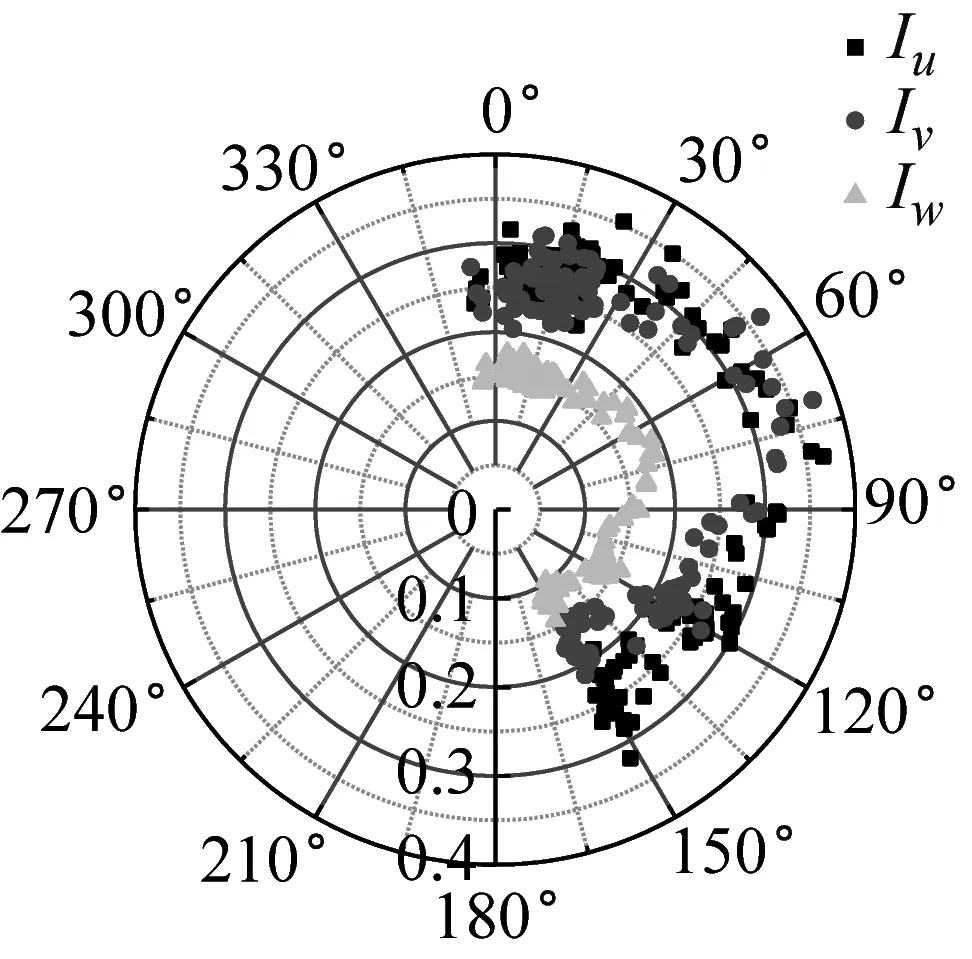
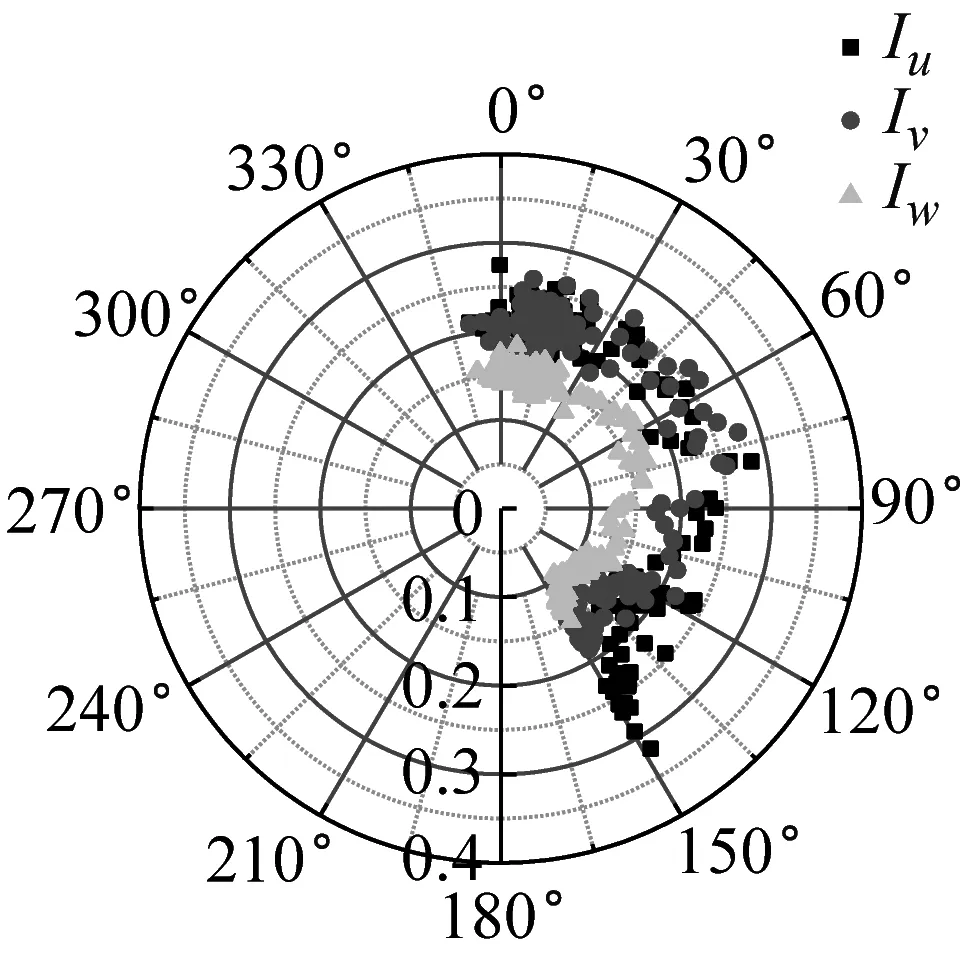
湍流強度反映了風速脈動的相對強度，是對大氣湍流最簡單的描述。不同來流方向對應的下墊面粗糙度不同，可能會影響到該處的湍流強度。SZMGT在臺風山竹期間的實測風向角記錄，在文獻[22]中給出了詳細說明，其中風向轉變明顯時段正對應風速時程的大風時段。根據式(4)，取基本時距為10 min的各向子樣本計算，基于不同方法討論不同高度湍流強度隨風向角的變化規律，結果如圖6所示。由圖6可見，湍流強度分量隨高度的增加而減小；采用不同方法計算得到的湍流強度存在一定差異，SMM計算的湍流強度最大、EEMD的計算值次之、DWT的最小，這和以上采用這3種方法計算脈動風速方差的差異特征是一致的。同時在東風及其附近(遠場地貌上對應的是高度900 m左右的羊臺山森林公園)，不同方法計算的各向湍流強度相對最大，該變化趨勢隨測點高度的增加更為明顯。

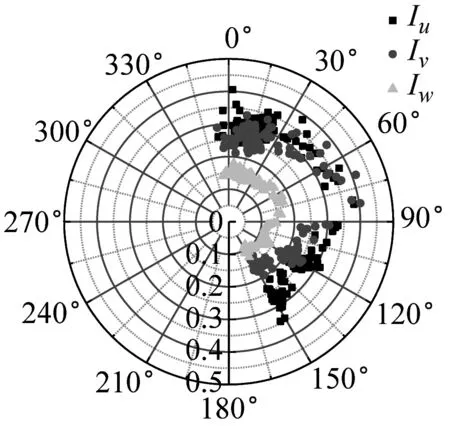
(a) 10 m-SMM

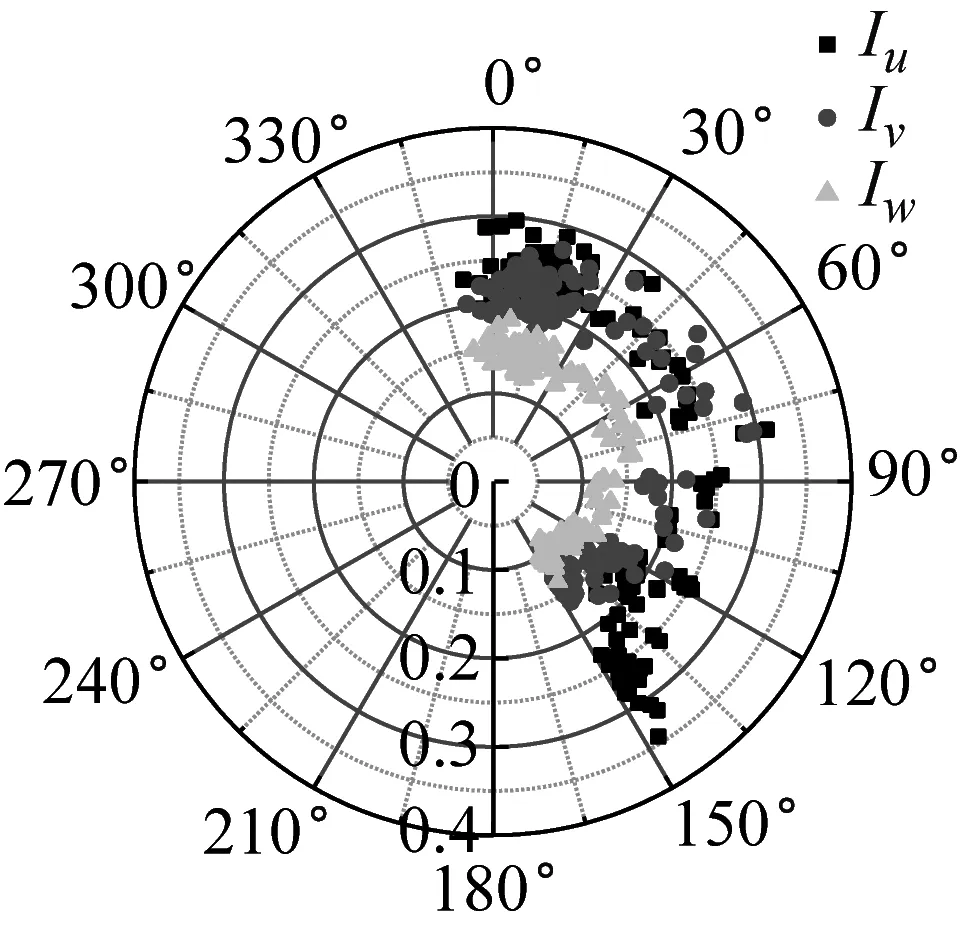
(b) 40 m-SMM

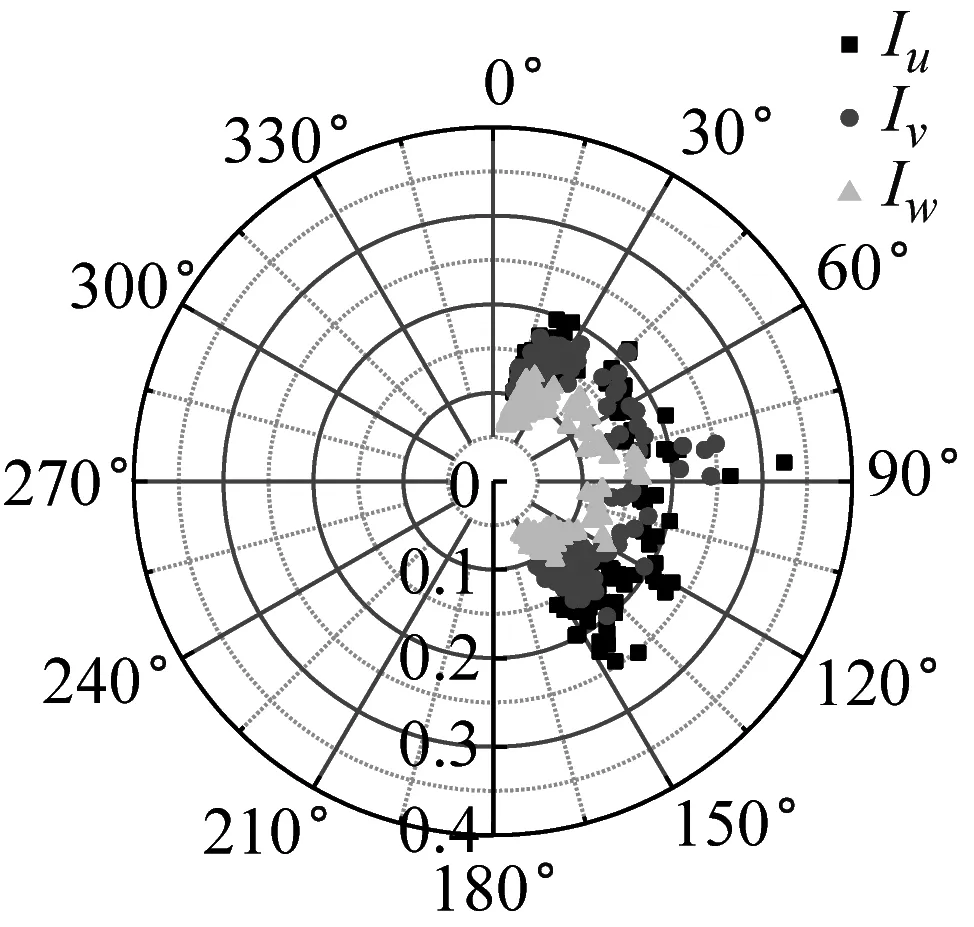
(c) 160 m-SMM

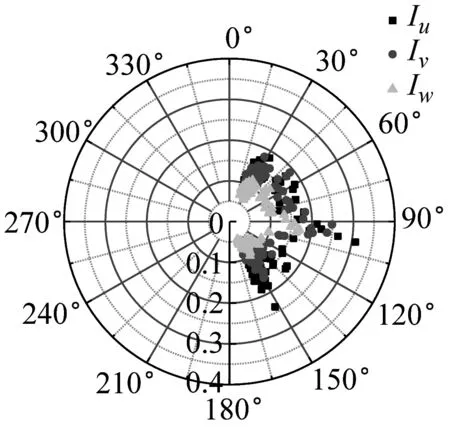
(d) 320 m-SMM

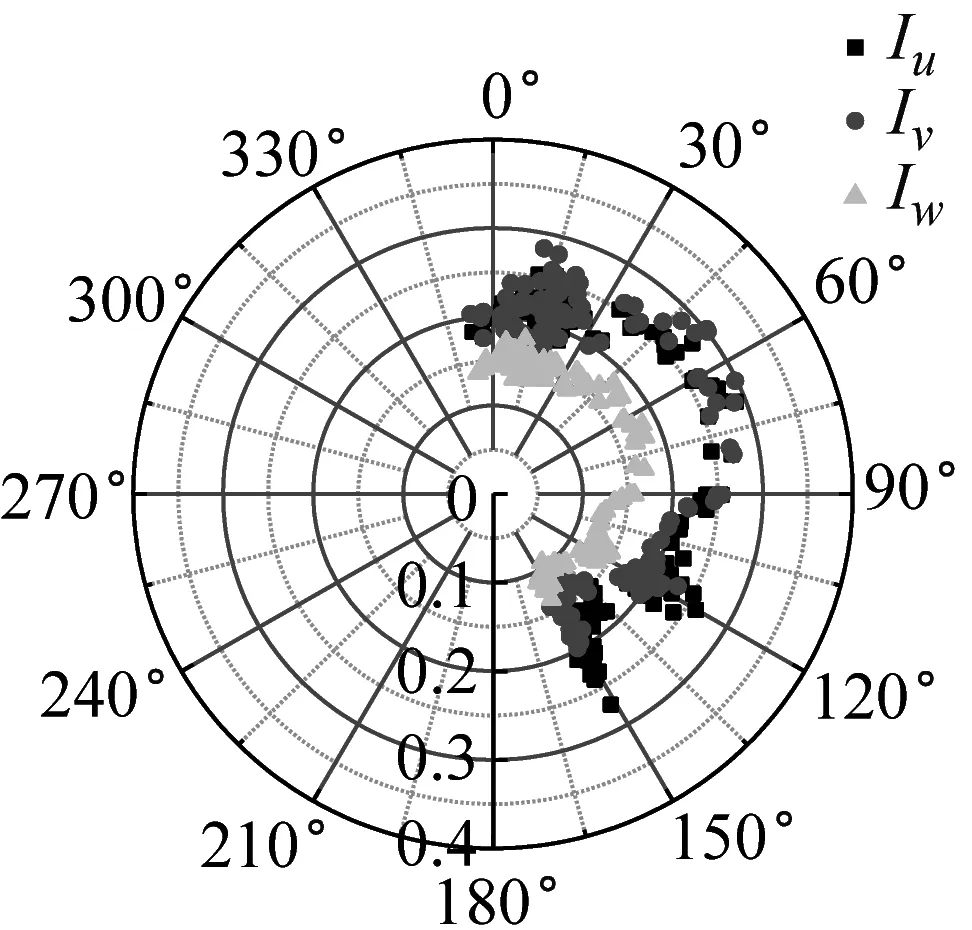
(e) 10 m-DWT

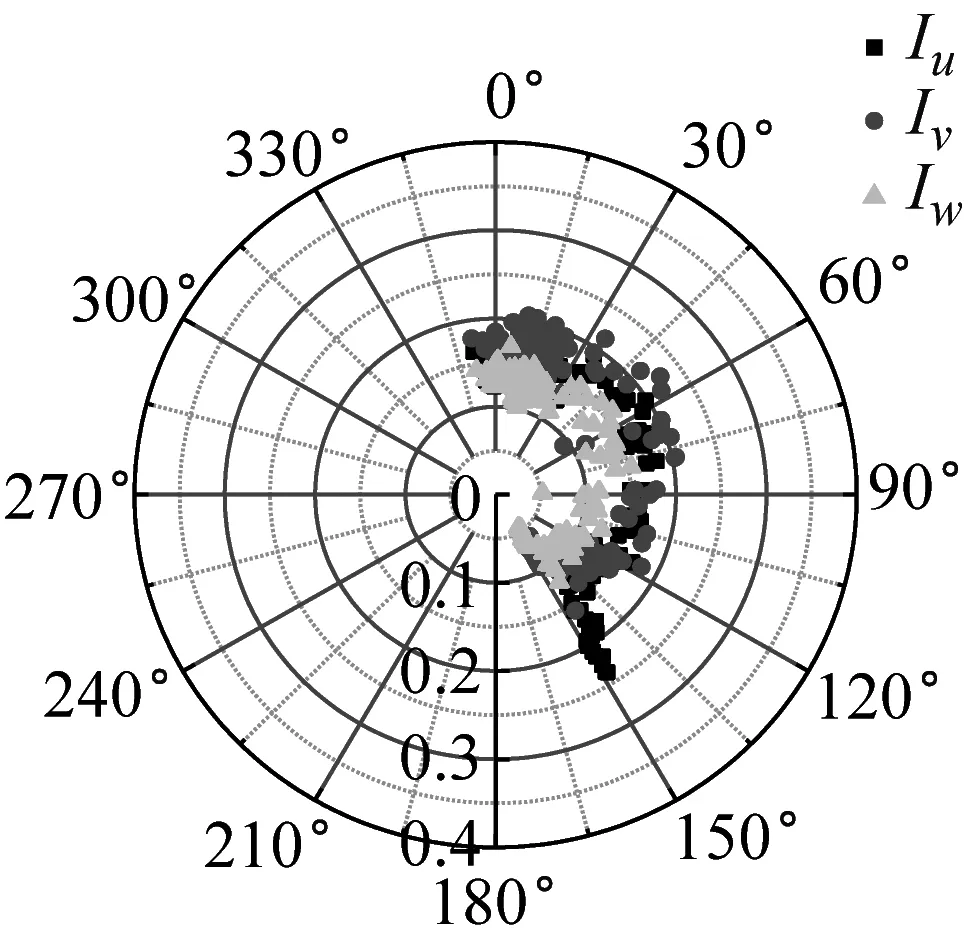
(f) 40 m-DWT

(g) 160 m-DWT

(h) 320 m-DWT

(i) 10 m-EEMD

(j) 40 m-EEMD

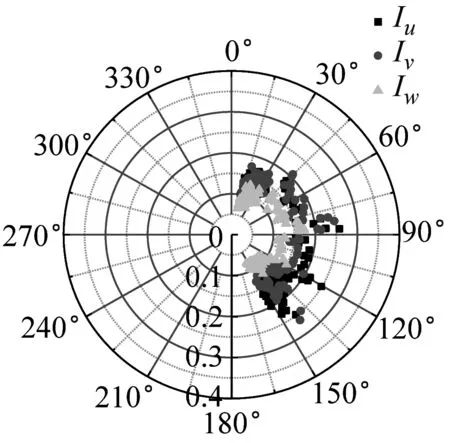
(k) 160 m-EEMD

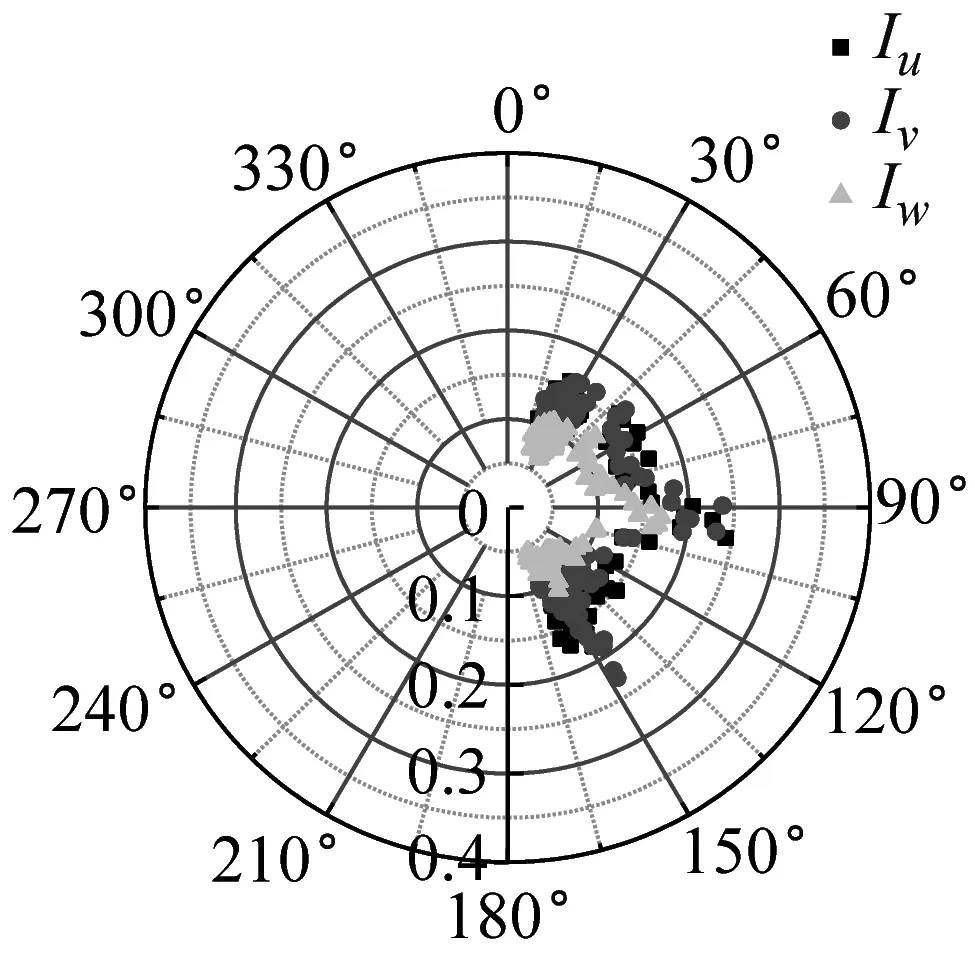
(l) 320 m-EEMD圖6 湍流強度隨風向角變化Fig.6 Variation of turbulence intensity with wind direction

進一步分析湍流強度分量的變化規律，計算不同高度子樣本三個方向湍流強度的均值之比，結果如表1所示。由表1可見，采用SMM得到的低空測點其三向湍強比值基本穩定在1∶0.84∶0.52，這與JTG/T 3360-01—2018《公路橋梁抗風設計規范》[23]中建議的Iu∶Iv∶Iw=1∶0.88∶0.50較為接近；高空測點湍強比值隨高度增加而增大；其他方法也出現了湍強比值隨高度增加而增大的現象。提取臺風的時變趨勢項后，各項湍流強度雖然較平穩模型計算結果小，但是臺風橫向湍流和豎向湍流相對增強，較橋梁規范建議比值偏大。

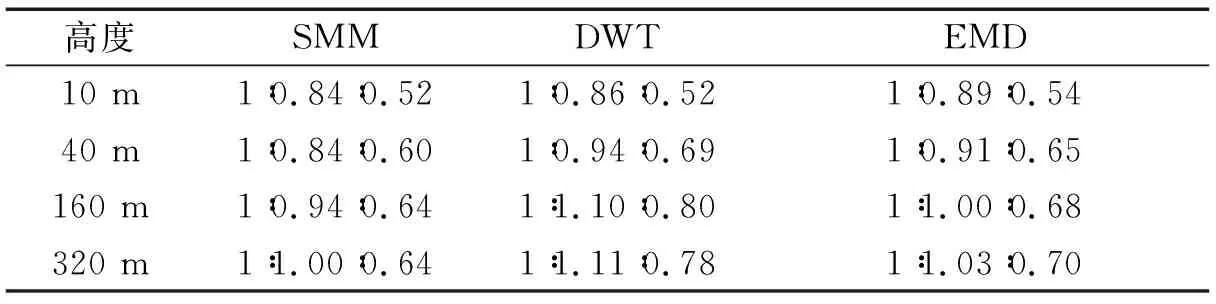
表1 三向湍強比值Tab.1 Turbulence intensity ratio

從建筑抗風設計的角度，縱向湍流強度沿高度的變化規律是工程師關注的重點。現將各種方法計算的湍流強度剖面和規范推薦的4類地貌對應的剖面進行比較，結果如圖7所示。由圖7可知，SMM和EEMD方法計算的縱向湍流強度剖面與D類地貌比較接近，DWT計算的縱向湍流強度剖面略小于C類地貌對應剖面。

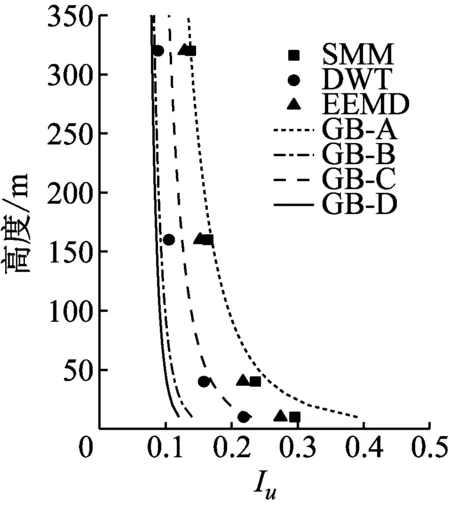
圖7 縱向湍流強度剖面Fig.7 Longitudinal turbulence intensity profiles

2.5 陣風因子

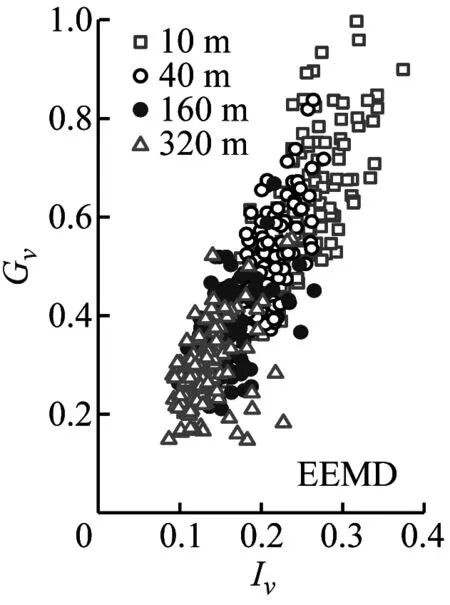
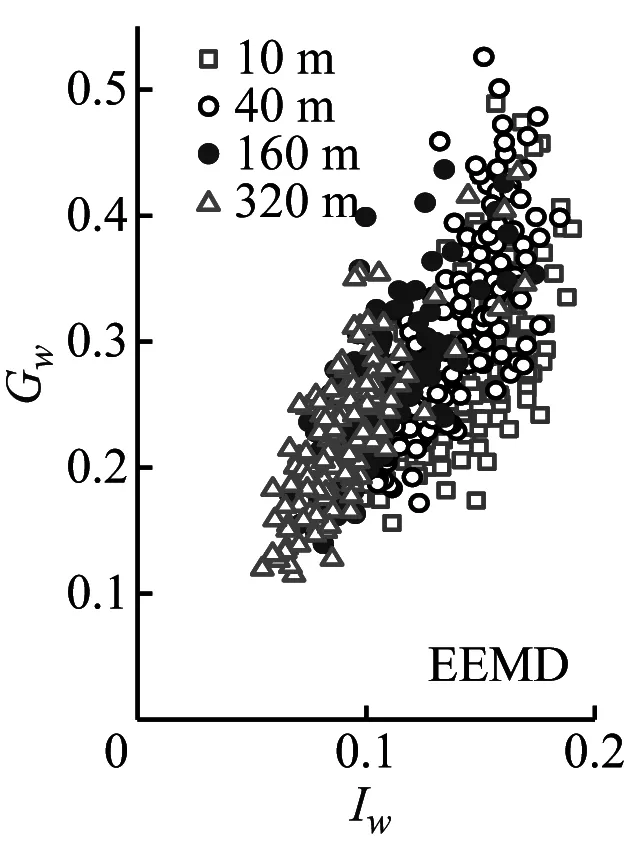
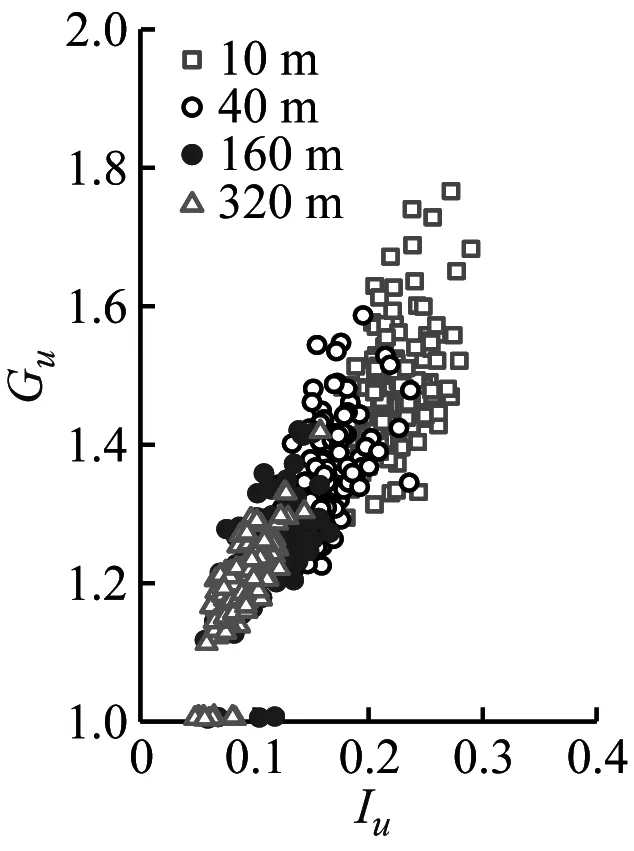
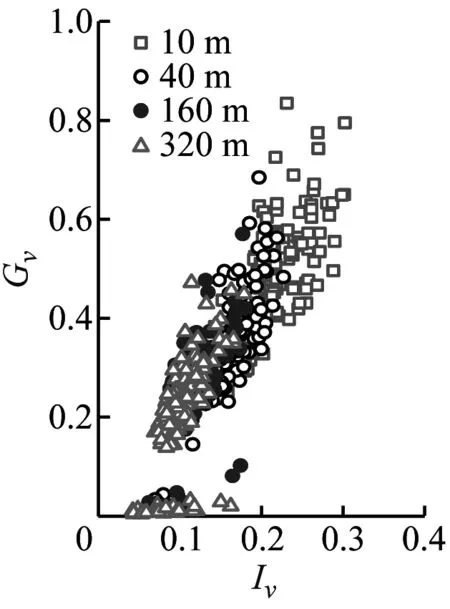
陣風因子與湍流強度及陣風持續期的關系是結構風工程中關注的熱點問題[24]。本節以3 s陣風持續期討論基于不同方法和高度計算的陣風因子隨湍流強度的變化規律如圖8所示。然后討論不同陣風持續期和基本時距與陣風因子的相互關系。

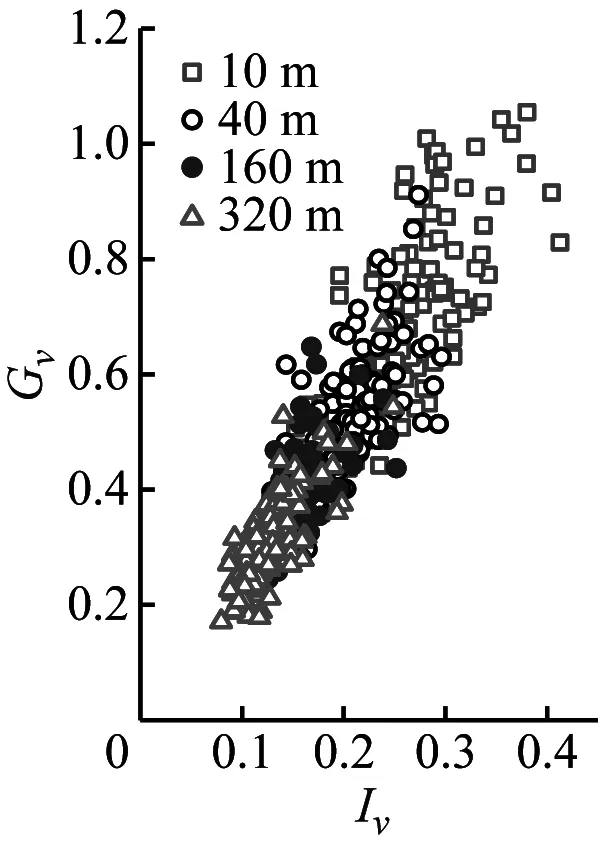
(a) Gu-SMM

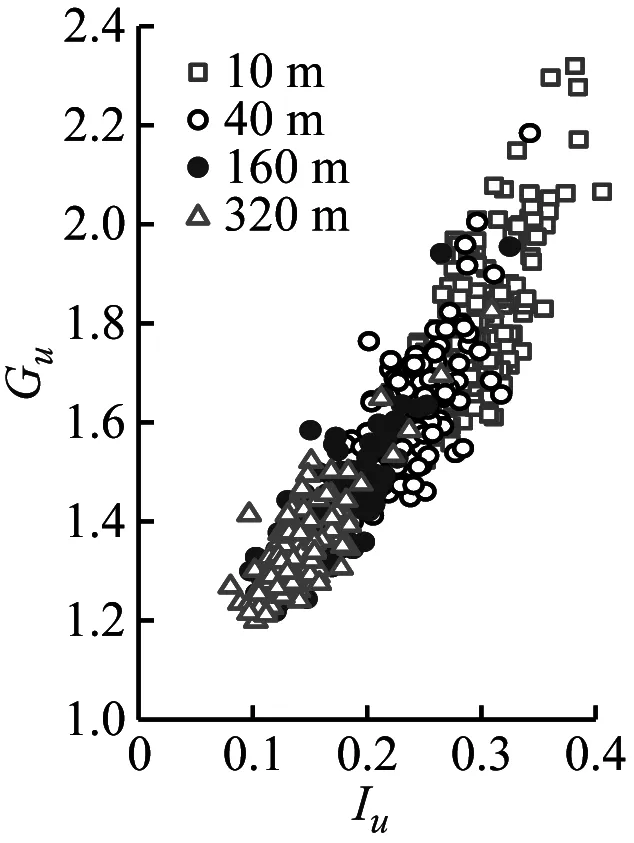
(b) Gv-SMM

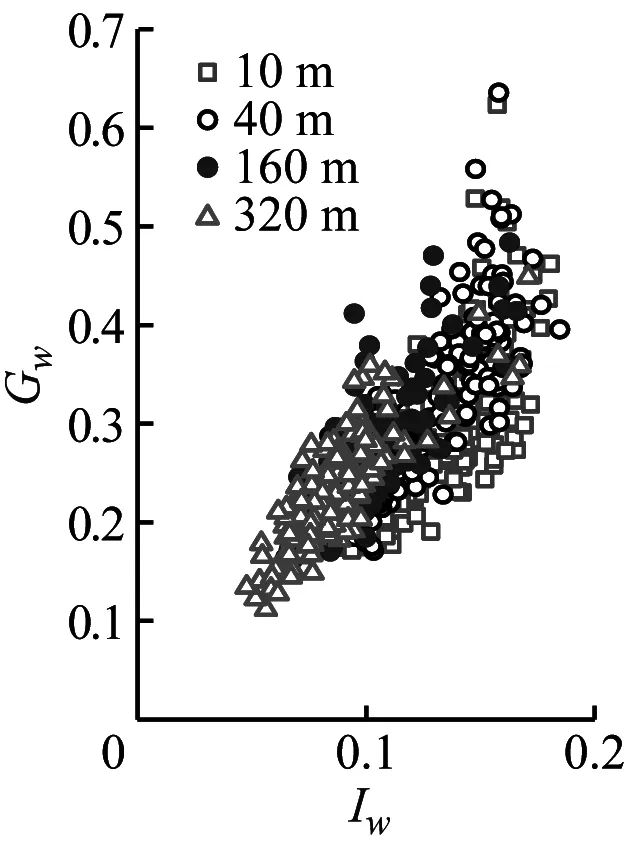
(c) Gw-SMM

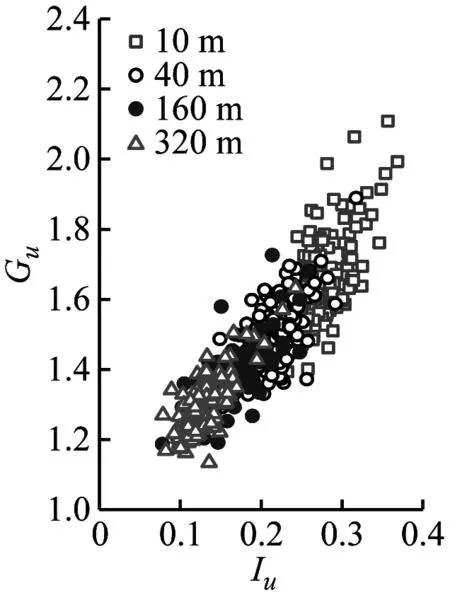
(d) Gu-DWT

(e) Gv-DWT

(f) Gw-DWT

(g) Gu-EEMD

(h) Gv-EEMD

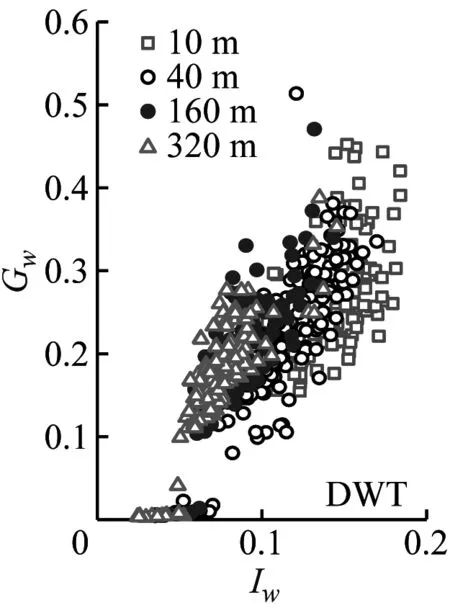
(i) Gw-EEMD圖8 陣風因子隨湍流強度的變化Fig.8 Gust factors versus the turbulence intensity

由圖8可見，陣風因子和湍流強度關系呈高度相關性；陣風因子隨高度的增加而減小。采用不同方法計算得到的陣風因子存在一定差異，SMM計算的陣風因子最大、EEMD的計算值次之、DWT的最小。

進一步分析縱向湍流強度和陣風因子之間的關系，Gu不只是和Iu有關，還取決于風速的平均時距T和所考慮陣風的持續時間tg，通常用下式表示

(8)

式中:k1和k2為兩個待定的常數，可通過擬合的方法獲取。在T=600 s，tg=3 s的工況下，本文擬合得到的k1為0.55，k2為1.14，和Cao等建議k1為0.5，k2為1.15較為接近。

陣風因子的大小與陣風持續期tg和基本時距的選擇有關。對10 min和1 h兩種基本時距，以縱向陣風因子為例，對比不同方法計算的各高度陣風因子隨持續期的變化規律，結果如圖9所示。由圖9可見，陣風因子隨持續時距的增加而減小，在單對數坐標下呈現非線性變化；隨基本時距的增加而增大；隨高度的增加而減小。由于存在高度相關性，采用不同方法計算得到的陣風因子的差異特征和湍流強度的差異特征一致，以10 m高度10 min基本時距實測結果為例，基于SMM、DWT和EEMD方法計算的縱向陣風因子均值分別為1.795、1.445和1.557。該結果可認為是按照實測平均風剖面判別的C類地貌的結果，按照規范給出的良態風氣候下陣風因子估算公式G=1+gIu(g取2.5)，C類地貌下陣風因子取值為1.575，與EEMD結果比較接近。

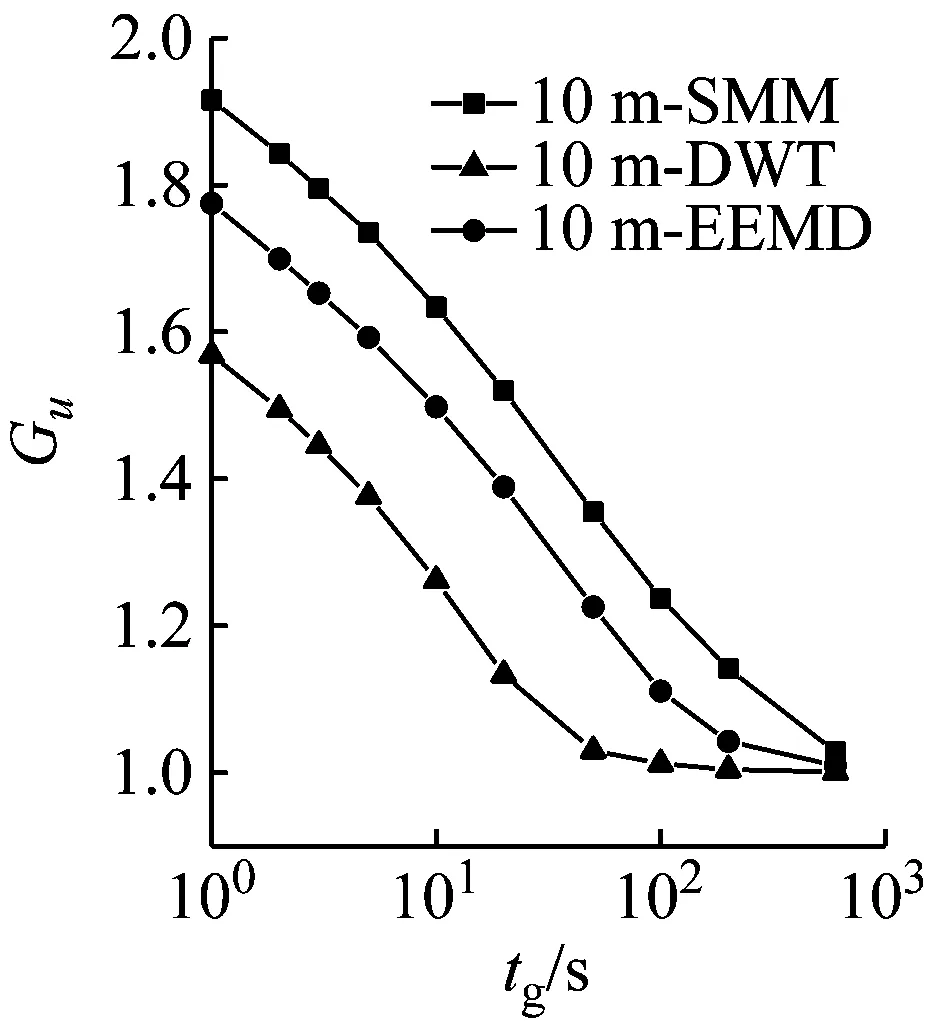
(a) 基本時距10 min(10 m)

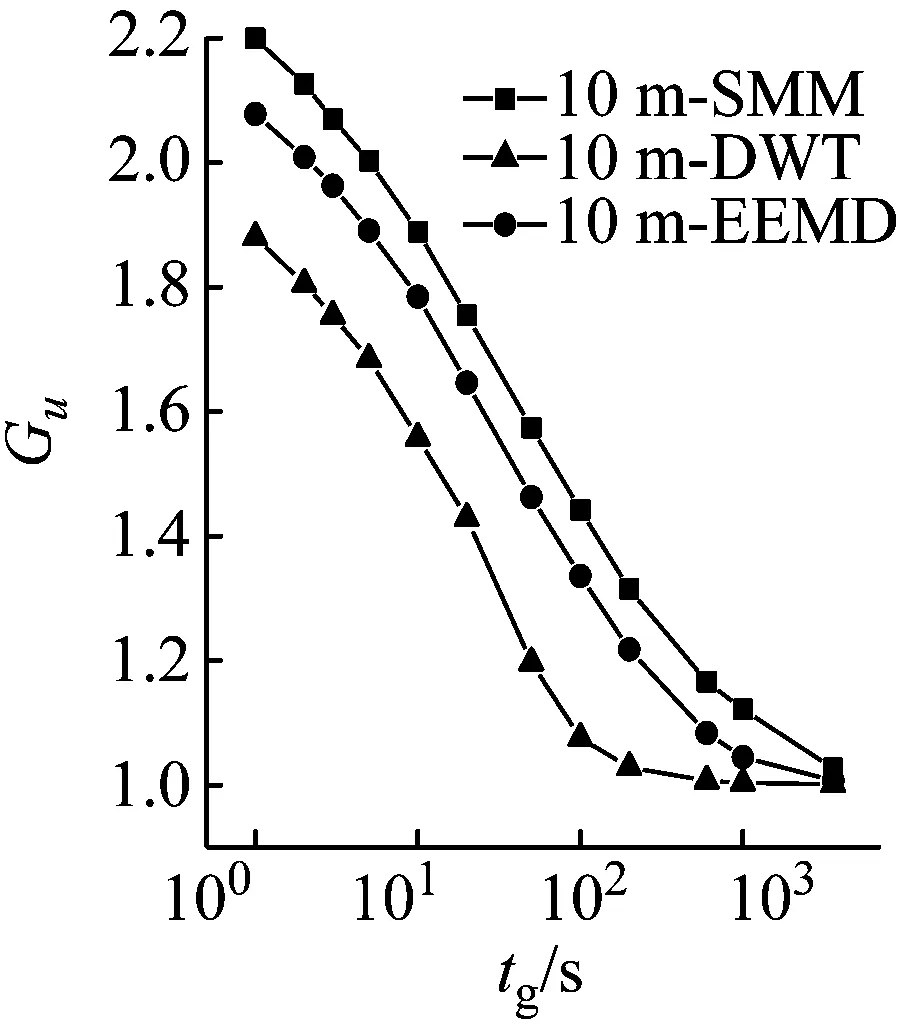
(b) 基本時距1 h(10 m)

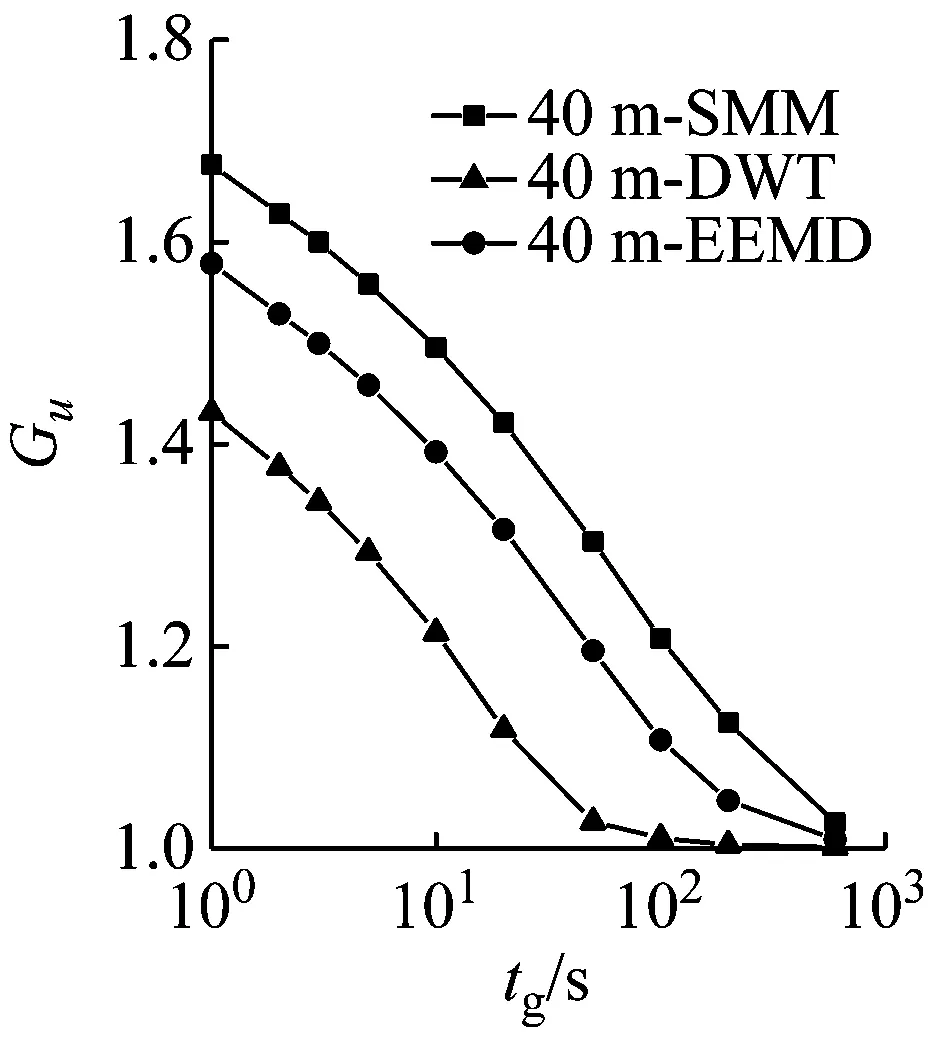
(c) 基本時距10 min(40 m)

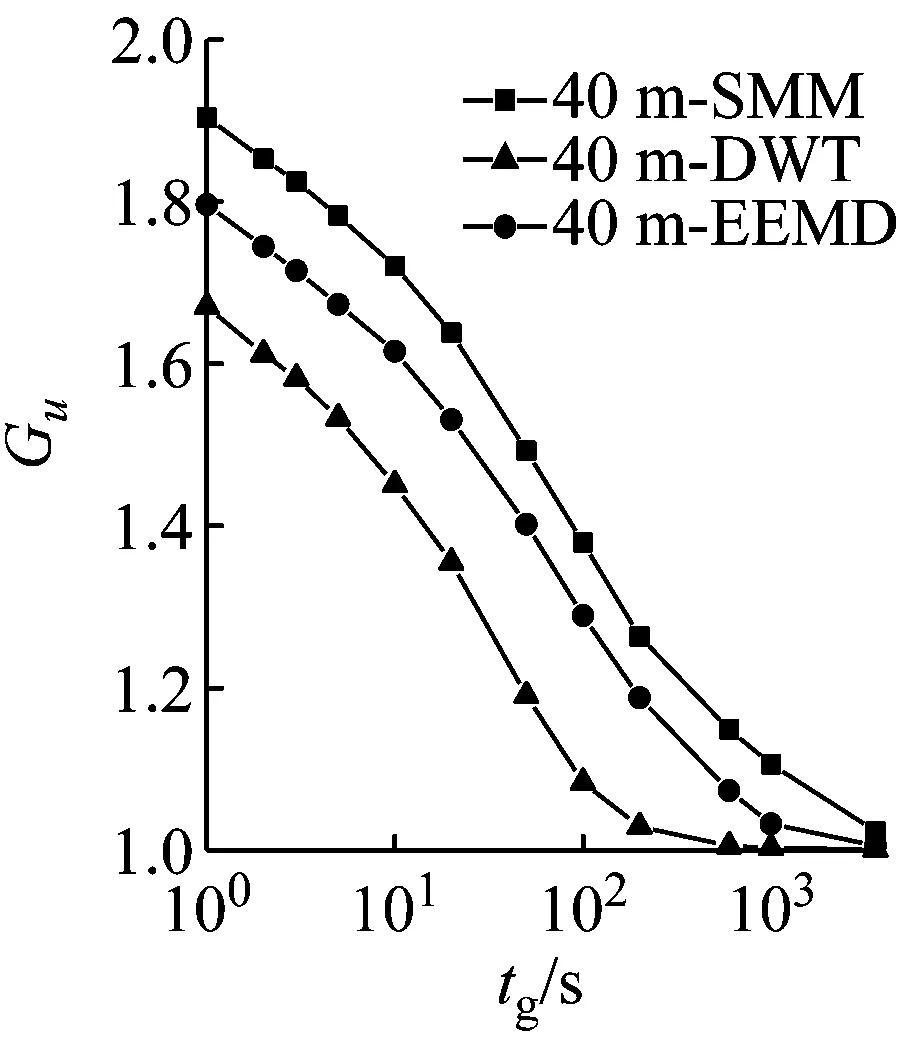
(d) 基本時距1 h(40 m)

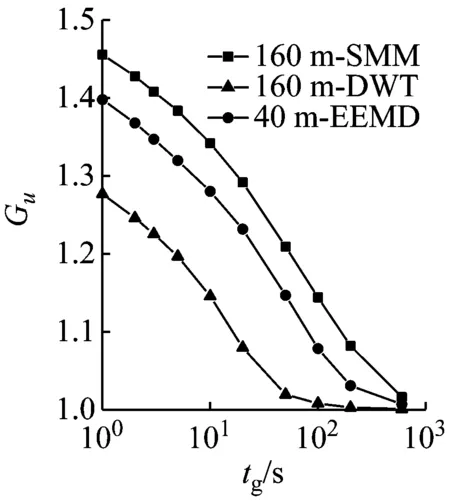
(e) 基本時距10 min(160 m)

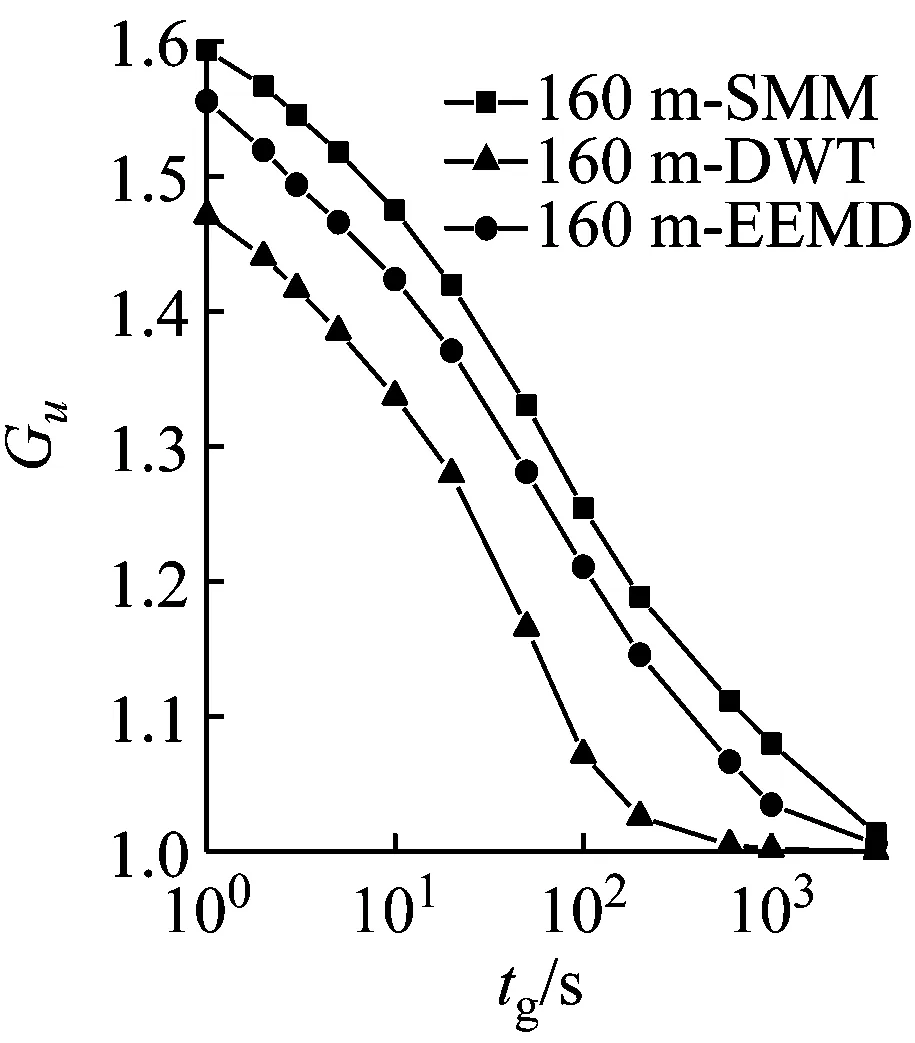
(f) 基本時距1 h(160 m)

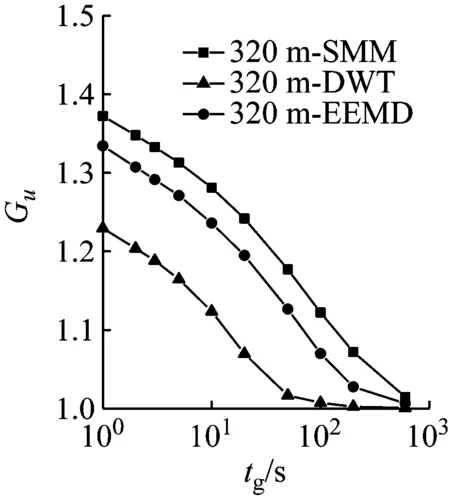
(g) 基本時距10 min(320 m)

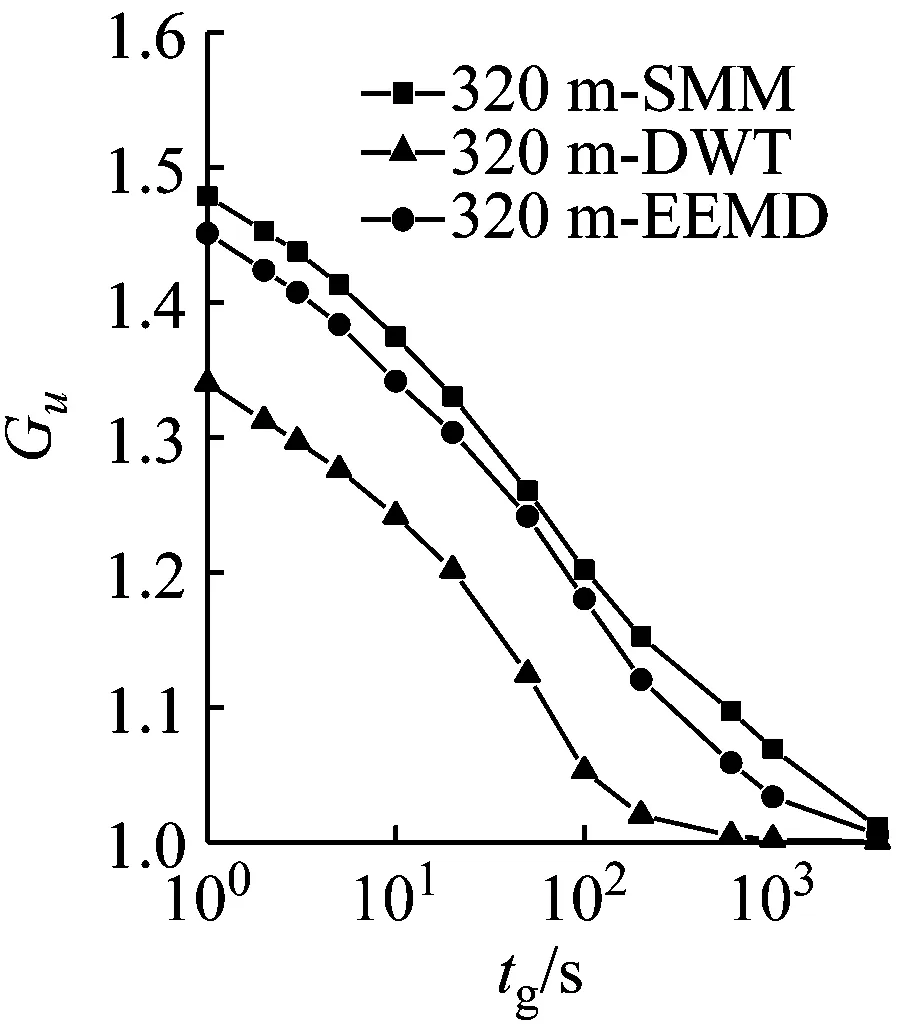
(h) 基本時距1 h(320 m)圖9 陣風因子隨時距的變化Fig.9 Gust factors versus the sample duration

2.6 湍流積分尺度

相對于以上所討論的其他風場參數，湍流積分尺度的離散性要更大一些。以縱向湍流積分尺度為例討論其離散性和分布規律，結果如圖10所示。由圖10可見，采用SMM計算得到的Lu相對離散，隨平均風速的增加而增大的趨勢最明顯；DWT計算的Lu相對最小，隨平均風速增加而增大的趨勢相對不明顯；EEMD方法計算的Lu介于SMM和DWT之間，隨平均風速增加而增大的趨勢相對明顯。

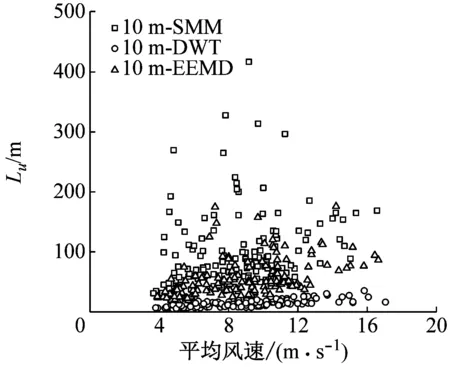
(a) 10 m

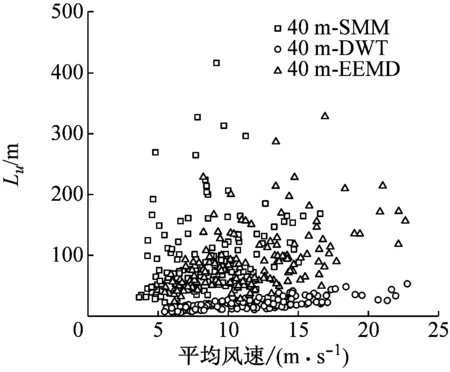
(b) 40 m

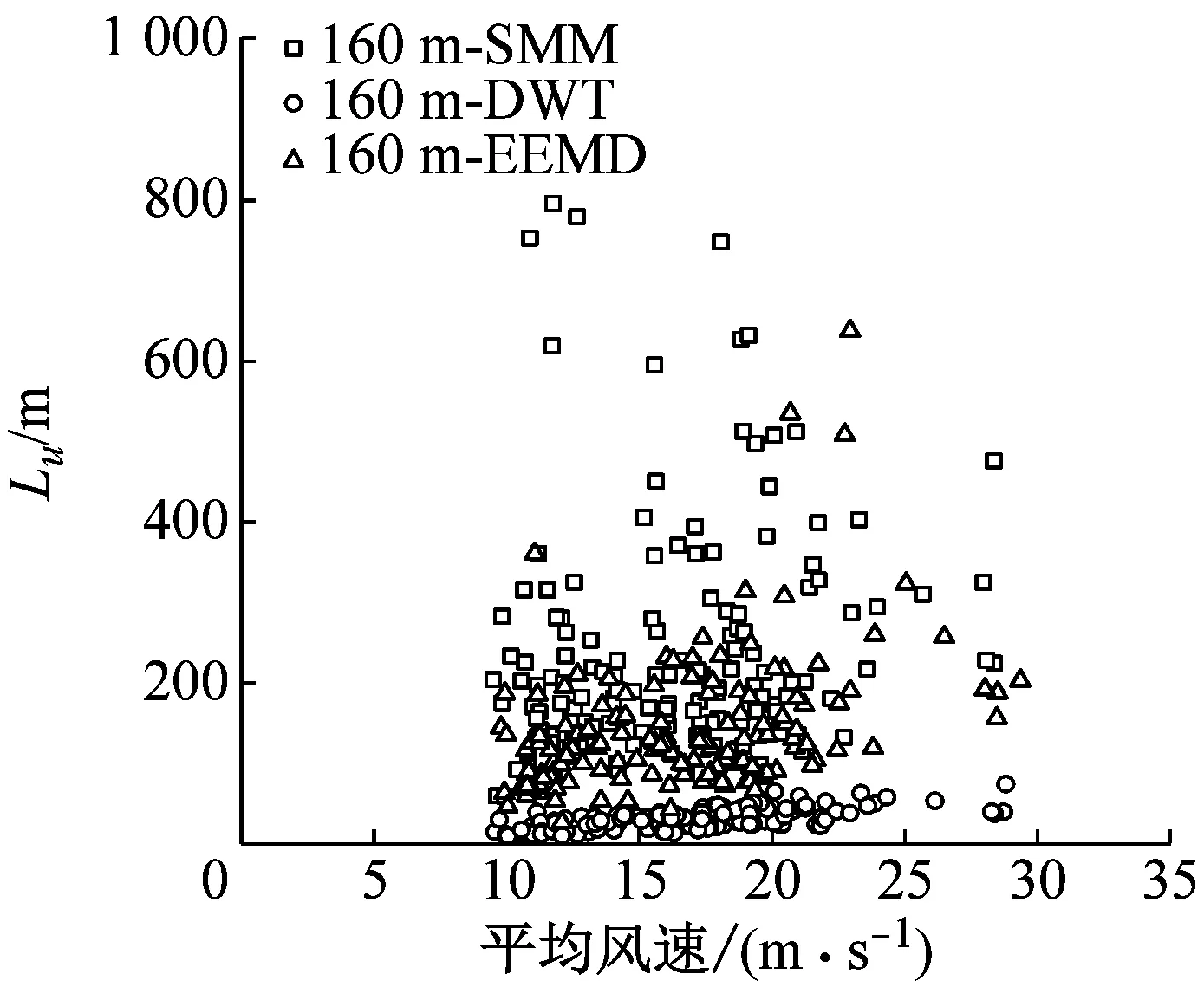
(c) 160 m

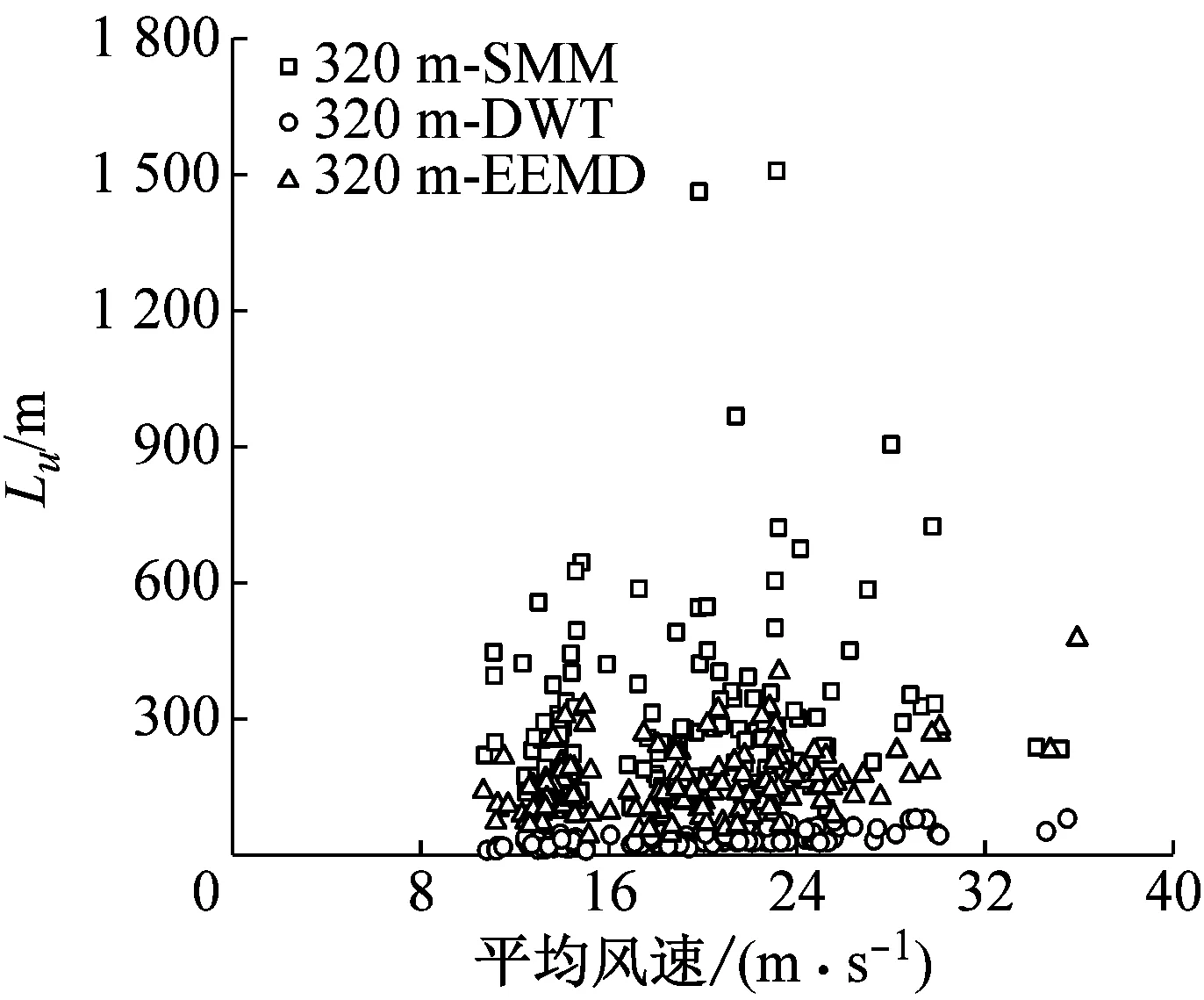
(d) 320 m圖10 縱向湍流積分尺度隨平均風速的變化Fig.10 Variation of Longitudinal turbulence integral scales with mean wind speed

取縱向湍流積分尺度均值分析其沿高度的變化規律，并與日本規范提供的推薦值對比，結果如圖11所示。由圖11可見，SMM計算的湍流積分尺度剖面和AIJ—2004《AIJ recommendations for loads on building》[25]的推薦剖面較為一致；EEMD計算結果次之，約為SMM計算結果的1/2；DWT的計算結果最小，約為SMM計算結果的1/7。這個結果與Tao等[26]采用DWT對蘇通大橋的實測湍流積分尺度的分析所得到湍流積分尺度偏少的結論相一致。

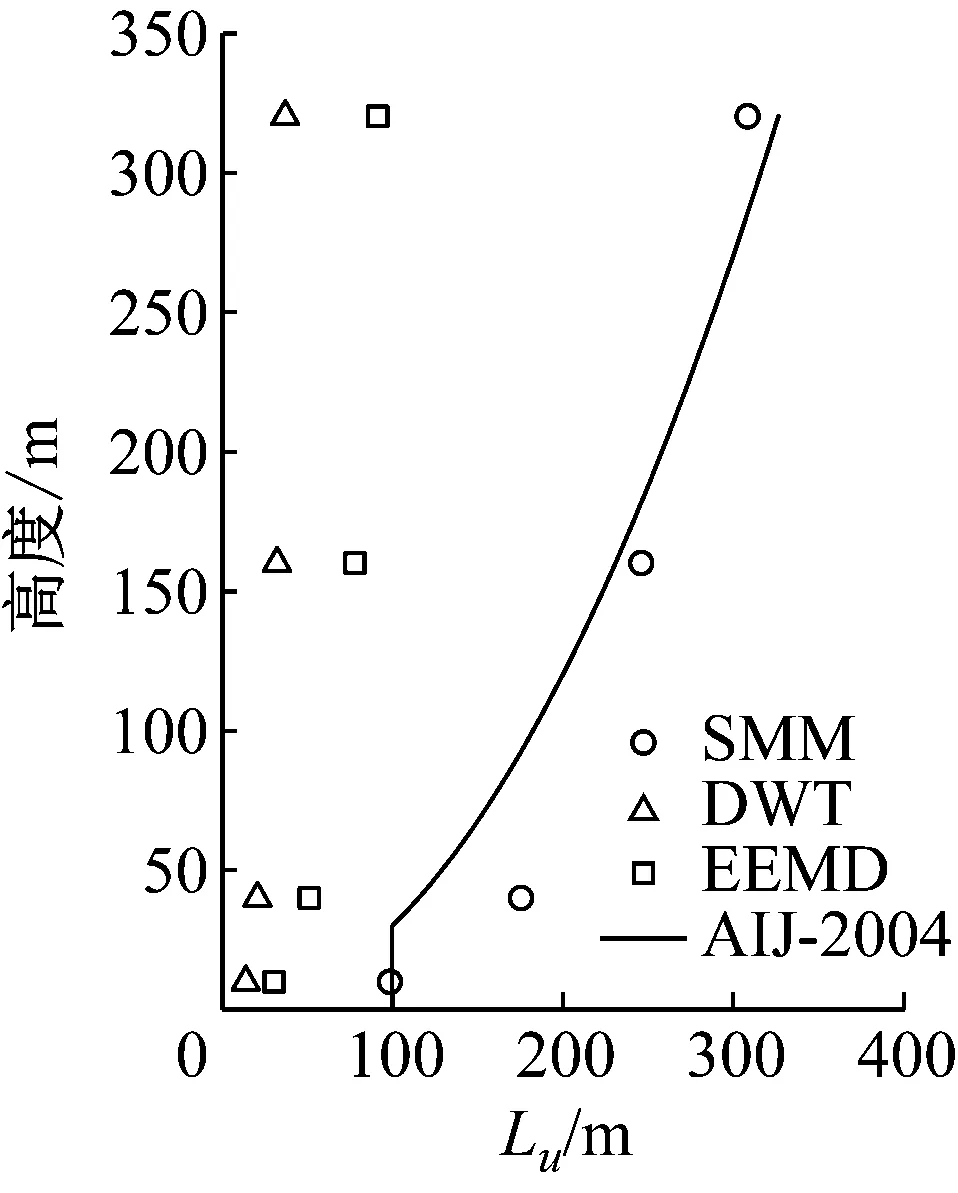
圖11 縱向湍流積分尺度剖面Fig.11 Longitudinal turbulence integral scale profiles

相比于圖7所表示的不同方法得到的湍流強度的變化和差異，不同方法所得到的湍流積分尺度分布的差異更為顯著。本文認為，在采用非平穩方法提取時變平均風速時把將真實脈動分量中的低頻部分一并提取掉是產生這個問題的主要原因，后續在對比湍流譜中可以得到進一步的證實。

2.7 脈動風速譜

對于脈動風速譜，以縱向脈動風速譜為例，取大風時段1 h(13:00—14:00)的實測數據進行分析，并與Von-Karman譜進行對比，結果如圖12所示。其中Karman譜公式中湍流積分尺度參照AIJ—2004推薦公式進行計算。由圖12可見，在不同高度處，SMM和EEMD的實測脈動風速譜比較接近且和Karman譜一致性較好，而DWT的實測脈動風速譜在低頻段明顯偏低，其湍流能量明顯偏小。脈動風速譜的變化規律可進一步佐證DWT方法在提取時變均風時，可能將屬于脈動風的某些長周期成分作為平均風一并提取，導致與頻域相關的風場特性參量明顯偏低、尤其是對低頻分量極為敏感的湍流積分尺度。

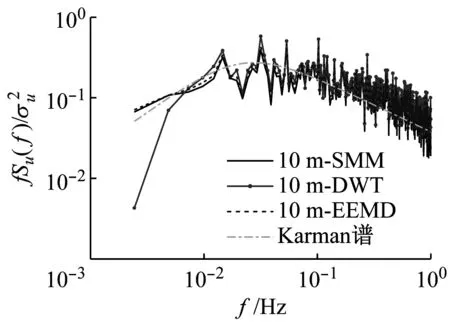
(a) 10 m

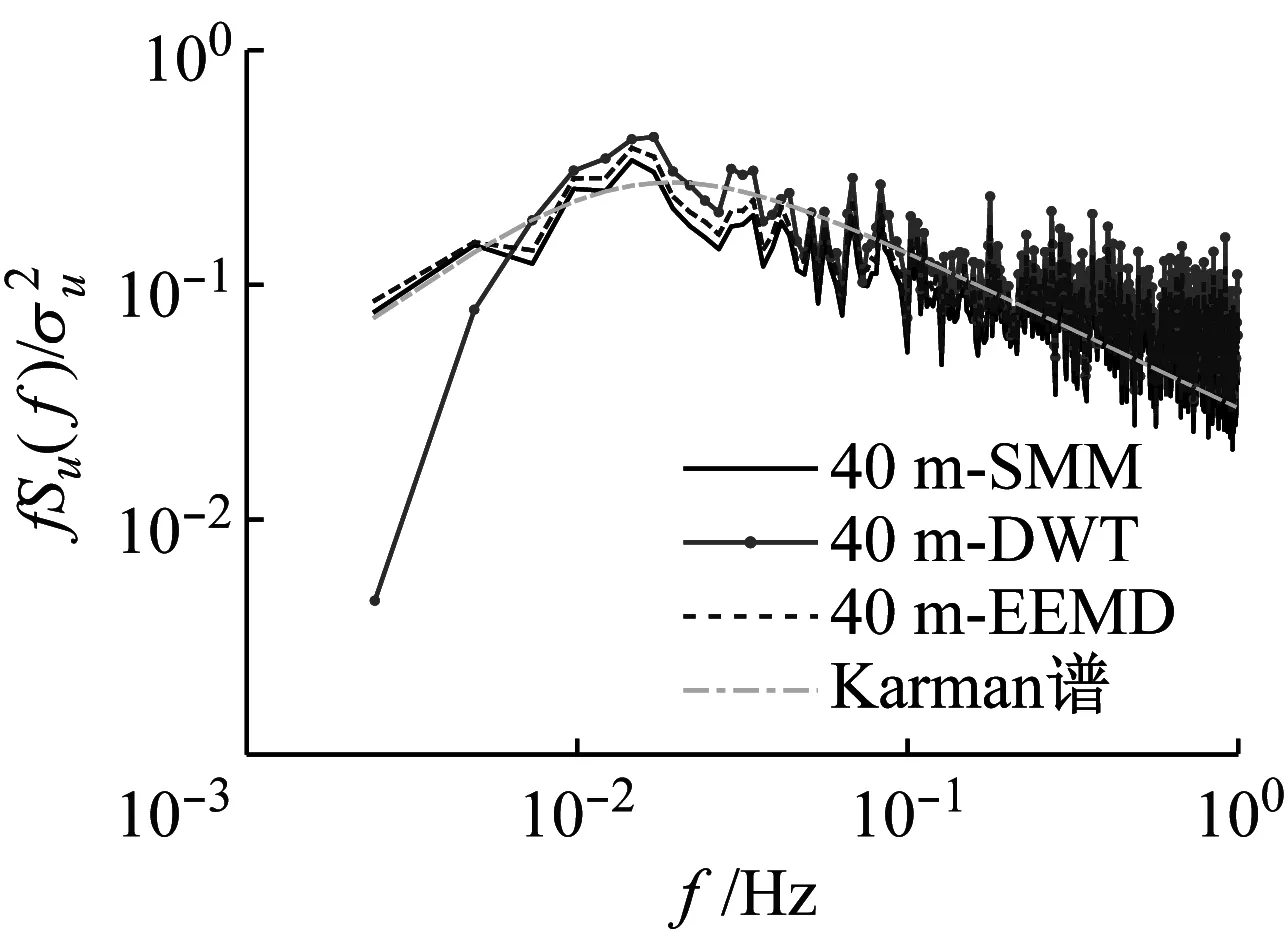
(b) 40 m

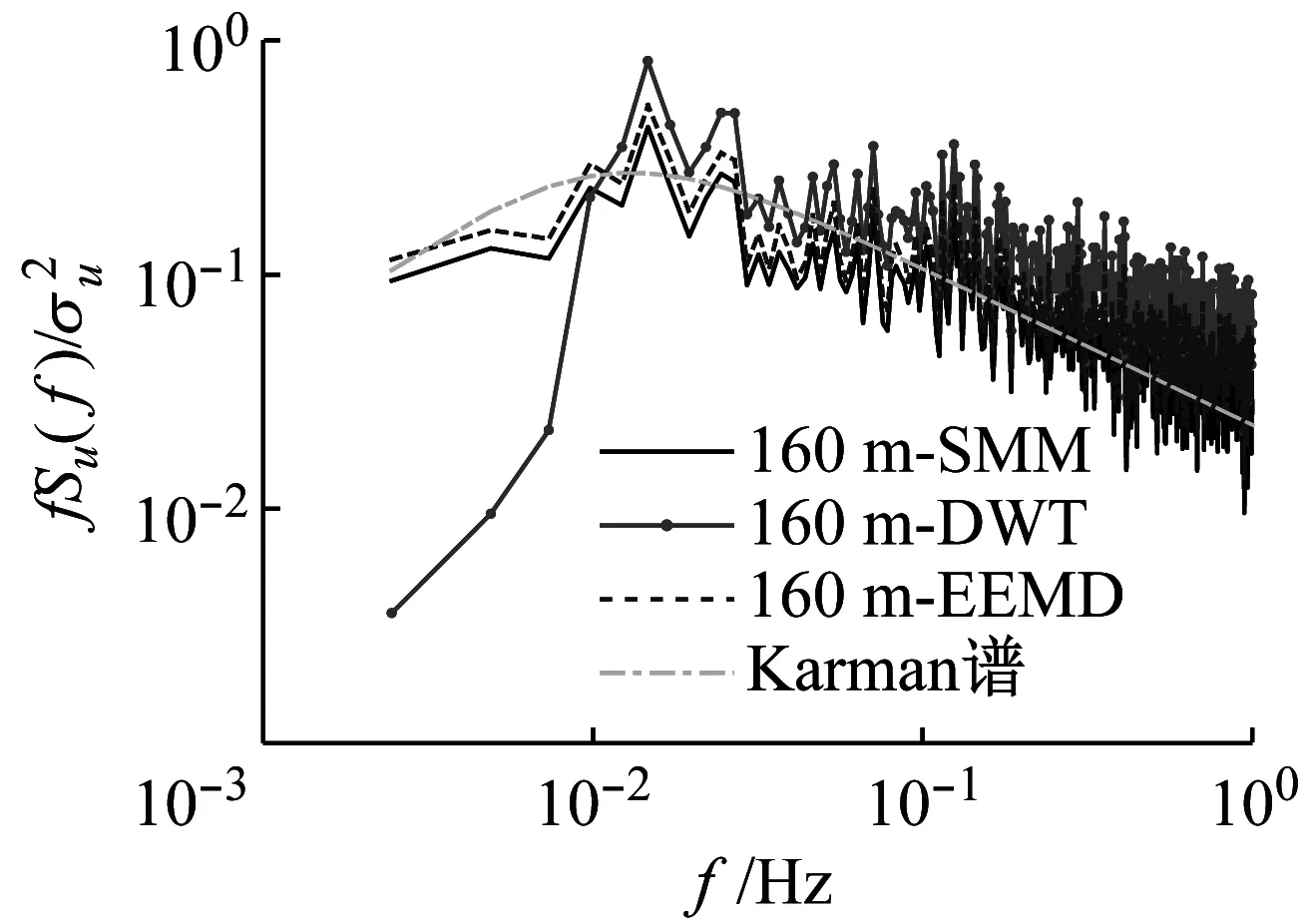
(c) 160 m

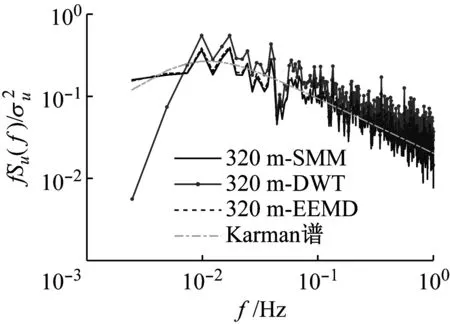
(d) 320 m圖12 縱向脈動風速譜對比Fig.12 Comparison of longitudinal fluctuating wind spectra

3 結 論

由本文研究可以得到以下結論：

(1) 考慮非平穩特性對于脈動風場特性的影響較大，對平均風速剖面的影響不大。

(2) 大風時段氣象梯度塔的實測平均風速剖面接近C類地貌對應的結果。

(3) 對于縱向湍流強度剖面，SMM和EEMD方法與D類地貌比較接近，DWT方法略小于C類地貌對應剖面。

(4) 陣風因子的差異特征和湍流強度一致，SMM計算值最大、EEMD計算值次之、DWT計算值最小。

(5) 對于縱向湍流積分尺度，SMM計算結果和AIJ—2004的建議值較為接近；非平穩模型的計算結果顯著偏小。

(6) SMM和EEMD的脈動風速譜和Karman譜一致性較好；DWT的脈動風速譜在低頻段明顯偏小。

在非平穩分析中，如何建立恰當合理的時變平均風速信號的提取方法、保證脈動分量參數不失真可能是后續需要進一步研究的問題。