基于Levy 飛行策略的灰狼優化算法*

崔 鳴 靳其兵

（北京化工大學信息科學與技術學院 北京 100029）

1 引言

實際生產中存在許多優化問題，傳統優化方法主要有牛頓法、梯度法等，但其中大部分是基于梯度的算法，但是這些方法均存在多種缺陷。近年來，不依賴梯度的元啟發式算法備受關注，引起了研究人員的極大興趣，這種算法不依賴梯度且能在復雜數值優化問題方面表現出較好的效果。群智能優化算法是元啟發算法的一種，群智能優化算法主要是受到自然界中生物種群的運動規律啟發而提出的算法［1］，常見的群智能優化算法有粒子群優化算法（PSO）［2］、蟻群優化算法（ACO）［3］、布谷鳥算法（CS）［4］、蝙蝠算法（BA）［5］等。

灰狼優化算法（GWO）是一種2014 年由Seyedali Mirjalili 等受自然界中灰狼捕食規律啟發而提出的一種新型群智能優化算法［6］。近期關于灰狼優化算法的改進與應用要有：裴虎等提出了二進制灰狼算法應用于特征選擇中［7］；袁巖等提出了基于對立搜索策略的灰狼算法應用于加氫裂化數據建模問題中［8］；瞿誠智等提出了基于強化學習的灰狼算法應用于無人飛行器路徑規劃中［9］；Rahul Kumar Vijay 等提出了量子灰狼優化算法應用于地震研究中［10］；Mohamed Abdel Basset 等提出了兩段突變的灰狼優化算法應用于特征提取中［11］；龍文等提出了基于布谷鳥算法改進的灰狼算法應用于太陽能光伏發電優化中［12］。但目前對于新型改進算法的研究并不完善，灰狼優化算法在精度和收斂速度等方面仍存在改進空間，因此對灰狼優化算法（GWO）的深入研究是極其必要的。

2 原始灰狼優化算法

2.1 灰狼種群

灰狼是一種群居動物，狼群一般由5～12 頭灰狼組成，在灰狼種群中有著非常嚴格的等級制度，等級制度表現為金字塔結構，如圖1所示。Seyedali Mirjalili 模擬狼群中等級制度，將灰狼種群劃分為α狼、β狼、δ狼和ω狼四個等級［6］，其中α狼為整個狼群的領導者，其命令等級最高；β狼是α狼的從屬狼，在整個狼群中起到加強化α狼的領導并提供低等級灰狼命令執行情況反饋的作用；δ對的等級更低狼服從于β、α狼的命令；ω狼是狼群中等級最低的灰狼，在狼群中是狩獵活動的主要實施者。

2.2 灰狼算法描述

灰狼算法對狼群中的等級制度進行模擬，將解集中的最優解記為α，其中的次優和第三優解分別記為β、δ，其他解記為ω。在算法中，搜索由α狼、β狼、δ狼指揮，ω狼服從。算法可分為接近獵物；包圍、騷擾獵物，直到獵物停止移動；攻擊獵物三個階段。

綜上所述，對包圍過程進行建模如式（1）、式（2）：

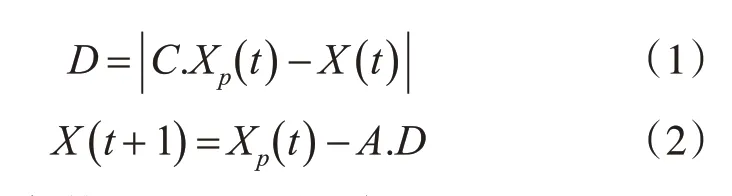
其中t為迭代數，A、C分別為A=2a·r1-a、C=2·r2的系數向量，系數向量中a在迭代過程中從2 線性減小到0，r1和r2為[0 ，1] 中隨機數。Xp為獵物位置向量，X為灰狼個體的位置向量。

在包圍完成、獵物停止移動后狼群就會進行狩獵活動，狩獵過程由α、β、δ狼共同做出決策，其數學表達式如式（3）：

其中Dα、Dβ、Dδ分別為α狼、β狼、δ狼與獵物之間的距離向量，Xα、Xβ、Xδ分別為α狼、β狼、δ狼的當前位置向量，C1、C2、C3為參數向量。

在隨機初始化后，計算每一只灰狼（候選解）的適應度值并排序，將最優、次優和第三優解的值分別賦值給α狼、β狼、δ狼。候選解ω的位置相對于α狼、β狼、δ狼的位置更新公式如式（4～5），其中A1、A2、A3為系數向量：

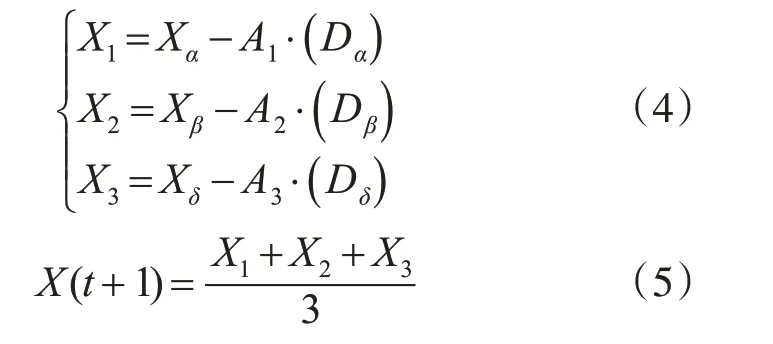
若候選解ω的適應度值比α狼、β狼、δ狼的適應度值更好，就更新領導灰狼的位置，不停迭代直到滿足中止條件找到全局最優解。

3 基于Levy飛行策略的灰狼算法

3.1 自適應位置更新策略

灰狼種群具有嚴格的等級制度，α、β、δ狼的領導權重依次遞減，但在原始GWO 算法中，ω狼的位置更新公式只是簡單地把α、β、δ狼的位置進行加和取平均，這并不能反映出種群中的等級制度。α狼處于領導層的頂端，適應度值最優，β狼處于第二領導層，適應度值次優，ω狼在進行位置更新時應當向更優的位置靠攏，更多地參考α狼、β狼的位置，因此本文為ω狼引入自適應位置更新公式如式（6）所示。

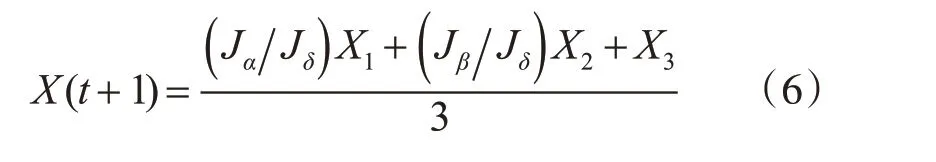
其中Jα、Jβ、Jδ分別為α狼、β狼、δ狼的適應度值。

3.2 非線性收斂因子

a是GWO 算法中的核心參數，在原始GWO 算法中，a的初始值為2，隨著不斷迭代線性減小直至0，但是這種線性減小的策略并不符合實際情況，在算法運行的前期階段中，參數較大算法進行全局搜索，隨著參數的不斷減小算法進行局部搜索，較為優秀的算法的全局搜索應長于局部搜索，這樣更能協助算法找到全局最優解。但原始GWO算法中參數a線性減小會使得算法的全局搜索和局部搜索的時間一致，這會導致算法還沒有很好地對整個空間進行搜索就轉為局部搜索，很容易到造成算法精度下降。

因此本文將參數a改進為非線性收斂，原始參數與非線性收斂參數對比圖如圖2 所示，公式分別為式（7）、式（8）所示，其中l為當前迭代次數，Maxinter為最大迭代數。

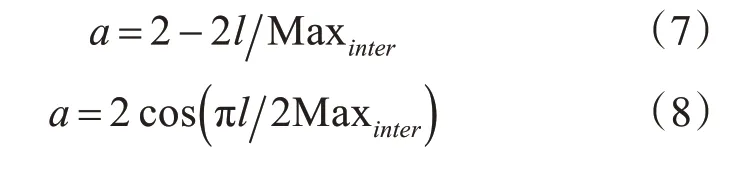
圖2 改進前和改進后的參數對比圖

3.3 引入Levy飛行策略

許多優化算法都會不同程度地陷入局部最優，影響算法對于多峰函數的性能，為了改善這一問題，我們將Levy 飛行策略引入LGWO 算法。Levy分布最早由法國數學家保羅。萊維于1937 年提出，但是由于這種他提出的積分形式沒有確定的解析解，產生一個服從于萊維分布的隨機數較為困難，隨著研究人員不斷深入研究發現，當(s→∞)時，，其 中Γ(z) 為Gamma 函數一般β=1.5，這個近似分布呈現重尾分布。Levy 飛行的方差隨著時間呈現指數關系，即σ2(t)～t3-β，1 ≤β≤3，因此Levy飛行對比隨即游走更加出色［13］。在實際應用中我們常用Mantegna 方法來生成服從萊維分布的隨機步長，Mantegna 于1994 年提出了一種用正太分布求解隨機數的生成服從萊維分布的方法［14］，生成服從Levy分布的公式如式（9）、式（10）：

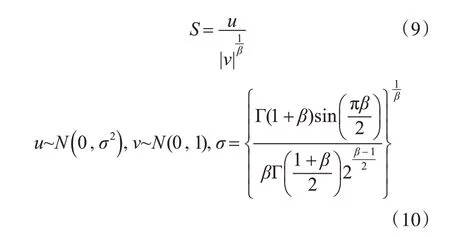
在LGWO 算法中，當適應度值連續limit 次沒有顯著變化（即變化值＜0.0001）時，我們就判定算法陷入了局部最優，從而引入Levy 飛行策略來幫助算法跳出局部最優。對于當前時刻使用式（11）產生下一時刻的候選解：

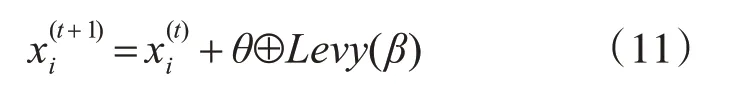
其中⊕為元素相乘，θ為[0 ，1] 間隨機數，β=1.5。

3.4 LGWO算法執行步驟

Step1：初始化上下邊界、最大迭代次數等參數，初始化灰狼種群，計算個體的適應度值。

Step2：對個體適應度值排序，將最優、次優、第三優的適應度值分別賦值給α、β、δ狼。

Step3：使用式（3）、（4）、（6）更新灰狼種群位置，更新系數向量A、C。

Step4：判斷算法是否陷入局部最優，若連續五次迭代適應度值沒有明顯變化，對灰狼種群引入Levy飛行策略。

Step5：判斷算法是否達到停止條件，若達到停止條件，輸出α狼位置，否則跳轉Step2。

4 實驗仿真與分析

由于智能優化算法與傳統優化方法不同，需使用測試函數來驗證優化算法的性能。我們使用IEEE CEC-2017 中的9 個測試函數進行算法性能驗證。測試函數可分為單峰函數（f1-f4）、多峰函數（f5-f7）和固定維多峰函數（f8-f9），測試函數的表達式如表1。仿真實驗環境為64 位Win10 臺式機、英特爾酷睿i7-4700MQ 8G RAM 環境中的Matlab R2019a 我們使用平均值（AVE）與統計標準差（STD）兩個評價指標來評估算法性能。

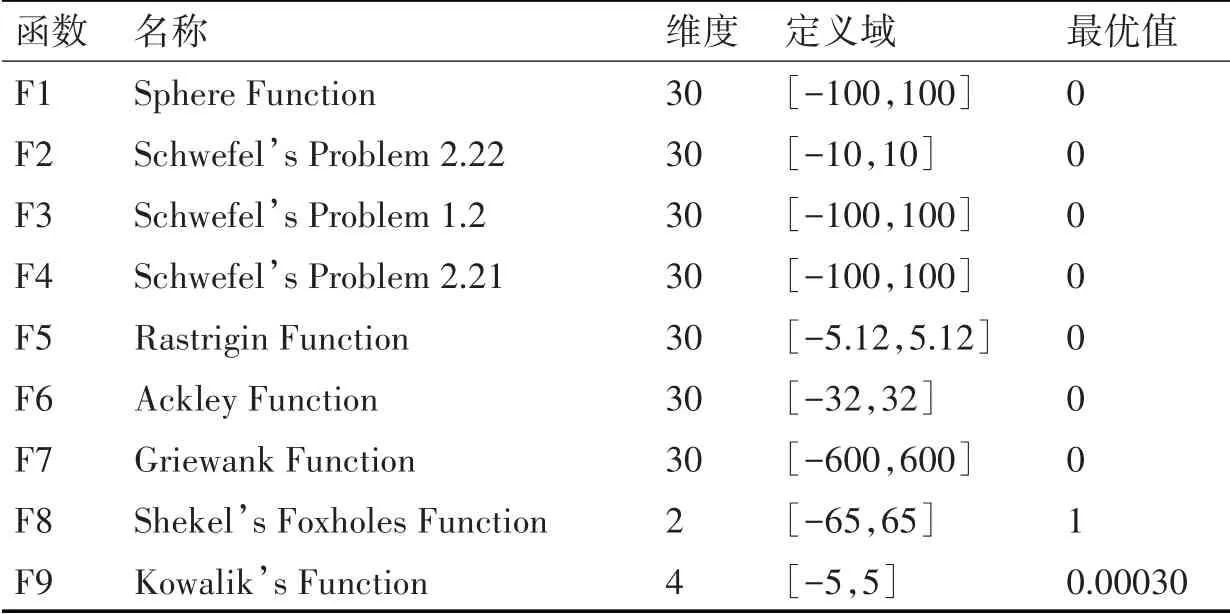
表1 標準測試函數

4.1 limit值對LGWO性能影響

在LGWO 算法中，limit 值為算法的重要參數，當算法連續limit次的適應度值沒有發生明顯變化，我們就判定算法出現了陷入了局部最優的情況，從而引入Levy飛行策略幫助算法跳出局部最優［15］。

為了確定LGWO 算法的最優limit 值，我們選取表1 中的測試函數F7，分別將limit 設置為3、5、10、15 來研究limit 值對LGWO 算法的影響，算法重復運行50次，計算50次的平均值與統計標準差，并求取重復運行50 次的總時間。實驗結果如表2 所示。

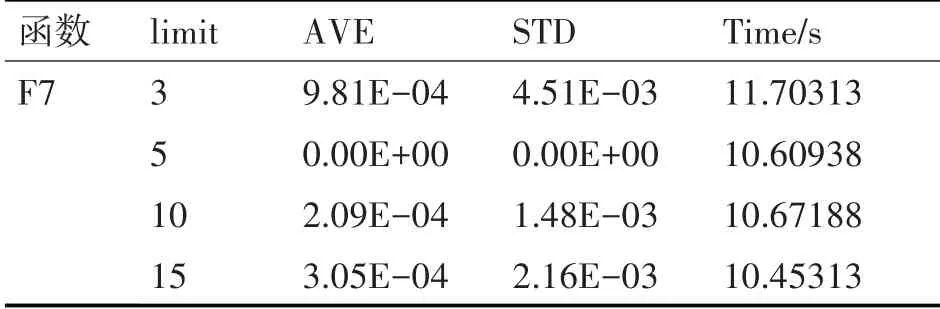
表2 limit值對LGWO算法的性能影響

由表2 可以看出當limit 取值為3 時，所用的總時間最長，limit取值過低導致算法頻繁判定陷入了局部最優，重復引入Levy 飛行策略，導致運行時間增加。當limit取值為5、10、15 時，程序運行時間相差不大，其中limit 取值為5 時，算法的平均值與標準差是三種情況最小的，收斂到了真值0。當limit取值為10、15 時，在算法的后半階段不足以進行足夠次數的Levy 飛行映射，也會導致算法性能下降。綜合考慮我們選取limit值為5。

4.2 LGWO算法性能測試

通過4.1 節的研究我們確定limit 的值為5，在本節中我們將測試LGWO算法的性能，并與原始灰狼算法（GWO）［6］、布谷鳥灰狼算法（GWOCS）［12］、粒子群優化算法（PSO）［2］進行性能對比，GWOCS算法是龍文等提出的一種基于布谷鳥算法改進的灰狼算法。在實驗中，算法的種群數量設置為30，將迭代次數設置為500。在實驗中，我們使用了相關參考文獻中的算法建議參數設置，每個實驗重復50次以避免偶然性，計算50 次重復試驗的獲得的平均值與統計標準差。

實驗結果如表3 所示，表3 中的Best 表示相對于其他對比算法，均值和標準差更好的情況個數。不同算法的收斂曲線如圖3所示。

表3 測試函數結果

從表3中可以看出，對于單峰函數（f1-f4），本文提出的LGWO 算法由于引入自適應位置更新策略、非線性收斂因子，算法具有了更強的開發能力，LGWO 算法的精度有了較大提升且算法最為穩定。對比其他算法更為優秀，顯著提高了算法處理單峰函數的性能（PSO（0/4）、GWO（0/4）、GWOCS（0/4）、LGWO（4/4））。

對于多峰測試函數（f5-f7），本文提出的LGWO 算法由于引入了Levy 飛行策略，能夠在算法陷入局部最優時效幫助算法及時跳出，大幅度提高了算法的探索能力，LGWO 算法性能明顯優于其他對比算法（PSO（0/3）、GWO（0/3）、GWOCS（0/3）、LGWO（0/3）），特別是函數f5、函數f7，LGWO 算法均搜索到真實值0 且標準差也為0，精度與穩定性均表現最優。

對于固定維多峰測試函數（f8-f9），LGWO 算法對比其他算法依然較為優秀（PSO（1/2）、GWO（0/2）、GWOCS（0/2）、LGWO（1/2）），對于函數f8，LGWO 算法的精度雖然相對PSO 算法稍差，但對比原始GWO算法、改進的GWOCS算法也有一定提高。

由圖3 可知，LGWO 算法的收斂速度是四種算法中最快的。例如，在單峰函數f6中，LGWO 算法在第200 次迭代時就收斂到了最優值，而其他對比算法在第320 次迭代時才能收斂到最優值，再一次說明了LGWO算法的改進的有效性。

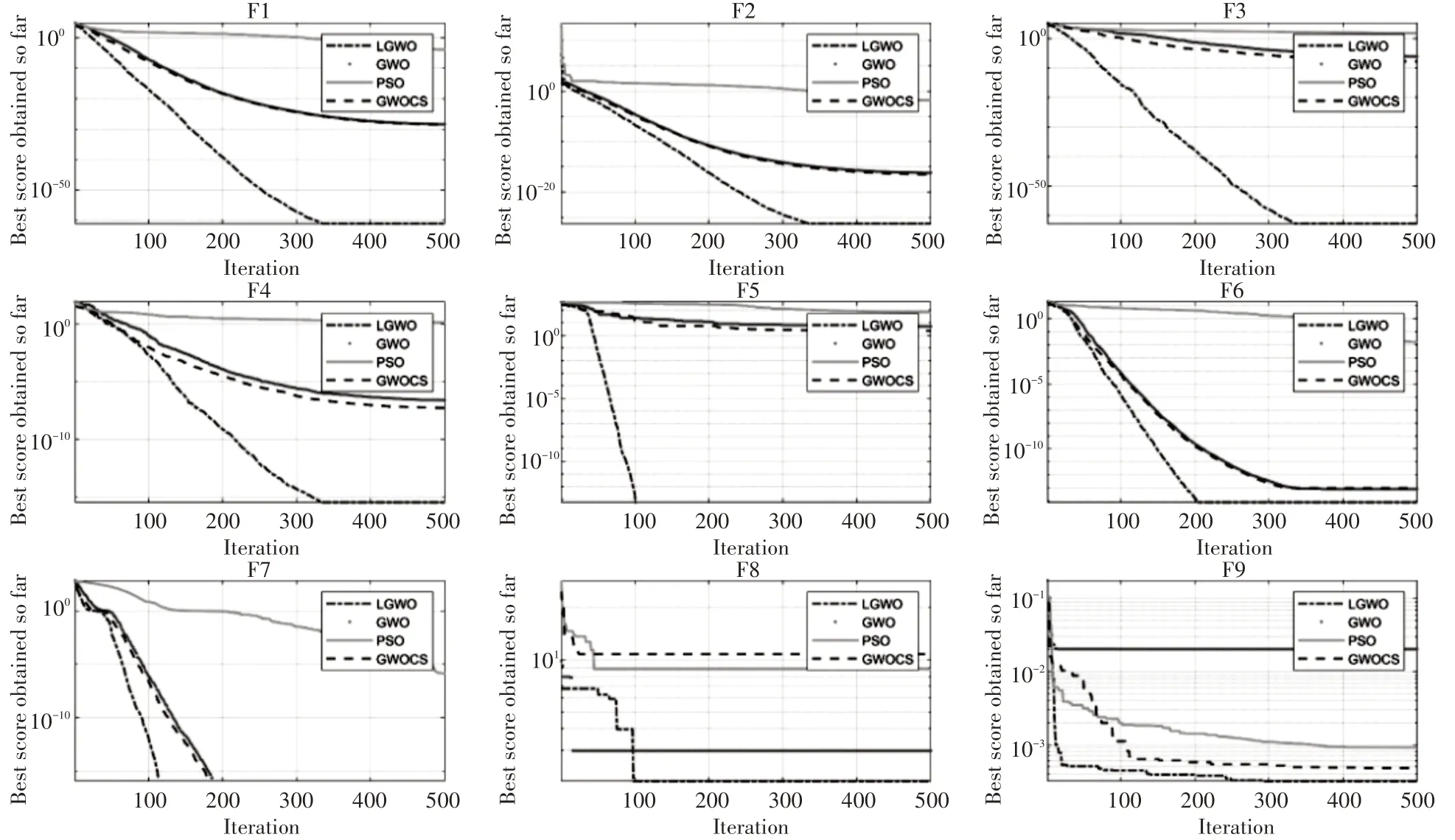
圖3 函數收斂曲線

5 結語

本文在原始灰狼優化算法中引入自適應位置更新策略、非線性收斂因子與Levy 飛行策略，使算法精度與穩定性都有了較大的提高。通過對9 個函數的仿真測試，實驗結果表明LGWO算法有效改進了原始算法容易陷入局部最優、收斂精度差的缺陷。在未來工作中，我們將著重研究嘗試將LGWO算法拓展到多目標優化領域，以解決精餾塔的多目標優化問題。