基于Leap Motion 的病患手評估算法研究*

于存光 韓越興 張小凡 歐陽皓寰

（1.黑龍江科技大學理學院 哈爾濱 150022）（2.上海大學計算機科學與工程學院 上海 200444）（3.上海大學上海先進通信與數據科學研究院 上海 200444）（4.廈門大學信息學院 廈門 361000）

1 引言

手也很容易受到外力的傷害和大腦損傷而造成功能喪失。現階段大多數診療依然停留在醫生目測或借助測角器等原始手段評定手的病情和治療的療效，因此存在很多的主觀因素。隨著人工智能的快速發展，各種硬件的革新換代，以及計算機算法的提出，使得利用計算機技術對手進行科學的、自動的評估成為了可能。標準化的評估手功能康復系統會幫助醫生進行診斷。

獲取手勢數據信息的方式大體上分為兩種：基于手套的手勢數據獲取方法和基于視覺的數據獲取方法。基于數據手套的獲取方法就是利用數據手套測量手指關節的彎曲度，手指間的角度，手掌的傾斜度等信息。2004年，高文［1］等選用了兩個數據手套和3 個位置跟蹤器成功識別了5113 個中國手語符號。肖陽［2］等的研究基于5DT 數據手套實現了對患者手部數據的采集，并以此建立模型評估患者手功能康復程度。文獻［3］利用數據手套和觸覺傳感手套裝置開發了一套中風后遺癥患者恢復性治療用的虛擬現實系統。數據手套的手勢識別方法具有受環境干擾小，識別率高，但是很多手部患者因為手的傷害無法穿戴數據手套，而且數據手套的高昂造價。

基于視覺的數據獲取方法是通過攝像設備采取手的各種視頻信息，從而實現手勢的識別和判斷。一般來說，最常見的視頻采集設備提取到的是手的二維信息，然后采用物體識別方法，如文獻［4～7］，來識別手勢。Priyal和Boral提出的HGR［14］系統來識別手勢。文獻［15］介紹了一種基于（GNG）算法構建的圖形表示和識別手勢的方法。但是，這些基于二維空間的方法很難計算出手勢的三維信息，也就是說，用二維圖像匹配的方法來進行三維手勢識別會丟失很多信息。因此，目前更多的是采用深度相機來采集手勢的三維信息。如2004 年，Mckenna［8］通過模版匹配的方法對60 種用戶定制的動態手勢進行識別。2008 年，Lichtenauer［9］等通過改進的動態時間規整算法對120 個荷蘭手語進行識別。但這些方法難以保證快速準確地估計人手姿態，同時它們無法實現近距離的高精度手勢識別［10］。

2012 年，Leap 公司推出了小型運動控制系統Leap Motion，可以追蹤多個手掌并識別手勢，其識別精度為0.01mm［11］。Leap Motion 的基礎技術是飛行時間（Time of Flight，TOF）技術［12］，是一種較專業的手勢采集設備［13］。Leap Motion傳感器不同于Kinect對視野范圍內追蹤到物體的整體框架描述，其方法是通過對手部信息包括指尖、關節點、方向向量、法向量等的精細化描述，利用這些信息實現對手勢的特征提取和準確識別。

本文中，我們設計一種基于Leap Motion 的非接觸式手功能評估系統，探測手各個部位在空間位置，比較兩手的手勢差異，完成對患側手的評價，從而幫助醫師評估其手功能康復情況，做出正確判斷，提出有效治療病患手的方案。

2 左右手勢差異的比較

對病患手的評估，需要考慮兩種情況。當患者非病患手功能正常時，比較病側手和健側手的各種姿勢的差異程度；當患者的雙手都存在病患或者一只手缺失的時候，就需要病患手和一只第三方的健康手進行比較。為了對任意手都可以進行數據的標準評估，首先進行坐標標準化和尺寸標準化。然后，通過計算兩手的關節點間差異度，指尖到掌心的歐幾里得距離和指尖的向量點積差異度就能得出兩手間差異度。

2.1 手的標準化

Leap Motion 定義了名叫finger 的對象，包含五個變量，thumb，index，middle，ring，pinky，代表了拇指、食指、中指、無名指和小指，通過finger可以獲取多種數據信息。利用Leap Motion，首先應獲取當前幀手池中手的數量，一般應當為兩只手：一只是基準手，一只待測手。在這里，基準手是健側手，待測手是患側手。當基準手和待測手進行比較的時候，根據雙手的左右不同，可以判斷是同側還是異側，即同側時，基準手和待測手的方向相同，而異側時，基準手和待測手的方向相反。兩只手變換重疊到一起才能比較，因此需要對手進行坐標變換。這里，我們假設測試的雙手都是異側的，因此，我們首先將一只異側手變化為同側手。

2.1.1 手的坐標標準化

Leap Motion 的默認坐標系采用的是右手笛卡爾坐標系，如圖1（a）所示，原點O在設備中心，X軸和Z 軸水平，Y 軸豎直。為實現手模型的坐標標準化，我們需要構建一個手的坐標系，原點O'為手掌心，掌心到中指指尖的方向為Z 軸，掌平面法方向為Y 軸，Z 軸和Y 軸所在平面的法方向為X 軸，如圖1（b）所示。

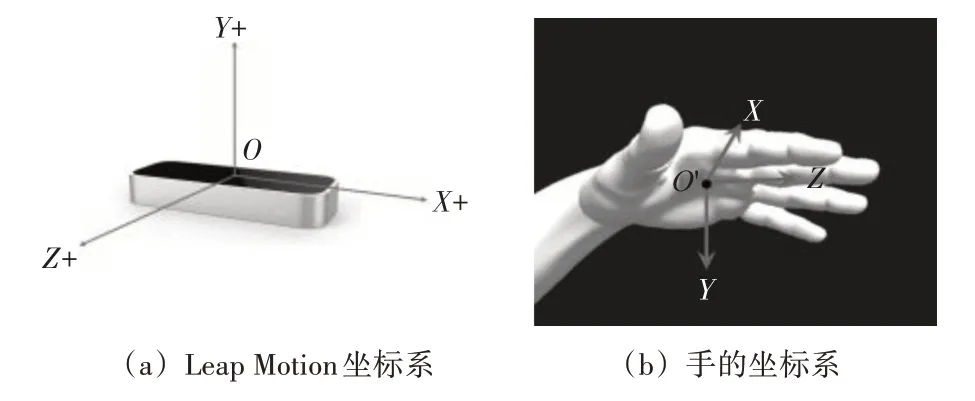
圖1 Leap Motion坐標系和構建的手坐標系

通過Leap Motion 檢測出手各點的位置是Leap Motion 坐標系的，需要把手的坐標變換到新建的手坐標系中，在數學表達上，兩個坐標系的坐標變換是通過一個矩陣實現的。首先考慮平移，即使Leap Motion 坐標系的原點O與手坐標系的原點O'重合。

通過平移矩陣T 和旋轉矩陣R 可將手上每個點P在Leap Motion 坐標系中的坐標變換成新建的手坐標系的坐標P'，設P在Leap Motion 坐標系中的坐標為（x，y，z），P' 在手坐標系的坐標為（x'，y'，z'），則坐標變換公式可表示為

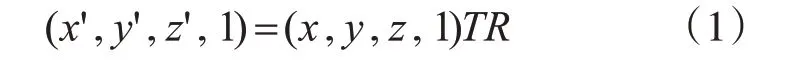
2.1.2 手的尺寸標準化

當基準手和待測手分別為兩個人的手時，由于不同人的手大小都有差異，要實現手差異比較必須對手進行尺寸標準化。我們通過基準手的中指長度和被測手的中指長度計算尺寸參數，用來對被測手進行尺寸標準化。設基準手的中指長度為l0，被測手的中指長度為l1，則尺寸標準化比例參數ρ可表示為

設被測手骨節點的坐標為J，則尺寸標準化后的標準手骨節點J'的坐標可用式（3）計算：

其中，Ji為被測手第i 個骨節點的坐標，Ji'為進行尺寸標準化后被測手第i個骨節點的坐標。

2.2 兩手差異度比較

比較兩手差異度的方法有很多，不同的方法體現的手勢差異的程度不同，本文通過兩手的各個關節點間差異度，指尖到掌心的歐幾里得距離和指尖向量點積三種方法來綜合評價基準手和患側手的差異程度。

2.2.1 基于關節點間差異度的兩手比較

每只手有五根手指，每根手指在Leap Motion手模型中由四塊骨頭組成，每塊骨頭由兩個關節點確定，骨頭的開始位置點為前關節，骨頭的結束位置點為后關節。

基準手和待測手中每一塊骨頭前關節之間的距離為前關節距離。設mdij為兩手第i根手指的第j塊骨頭的前關節距離，可以用以下公式計算：

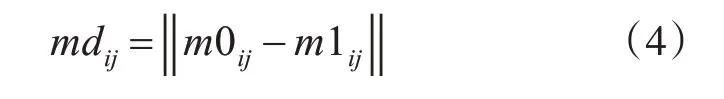
其中，m0ij為基準手第i根手指的第j塊骨頭的前關節坐標，m1ij為待測手第i根手指的第j塊骨頭的前關節坐標，||*||是三維向量的歐幾里得距離（下同）。

基準手和待測手一塊骨頭后關節之間的距離為后關節距離。設ndij為基準手和待測手第i根手指的第j 塊骨頭的后關節距離，可以用以下公式計算：

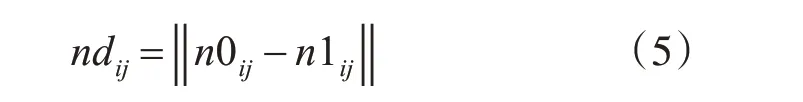
其中，n0ij為基準手第i根手指的第j塊骨頭的后關節坐標，n1ij為待測手第i根手指的第j塊骨頭的后關節坐標。

最后，通過下面公式就可以得出基準手和待測手的關節點間差異度C：

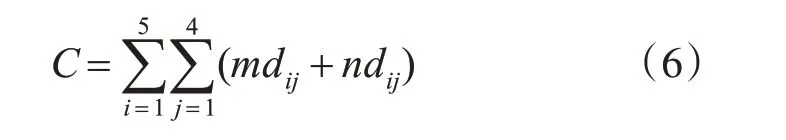
其中，i是手的手指從1～5 變化，表示手的5 個手指；j從1～4變化，表示每個手指有4個骨頭。

2.2.2 基于指尖到掌心的歐幾里得距離差異度的兩手比較

由于指尖的位置會隨手勢變化而變化，因此我們也可以通過計算標準手和待測手每對手指的指尖到掌心的歐幾里得距離差的絕對值之和來表示手勢的差異度。手指指尖到掌心的距離s可以用圖2所示。

圖2 掌心到中指指尖的距離及方向

設掌心的坐標為o，手指指尖的坐標為vi，i=(1，…，5)，則每個指尖到掌心的歐幾里得距離s可表示為

設s1i，s2i，i=(1，…，5)，分別為標準手和待測手的指尖到掌心的歐幾里得距離，則歐幾里得差異度可用標準手和待測手指尖到掌心歐幾里得距離差的絕對值之和E可以用下式計算：

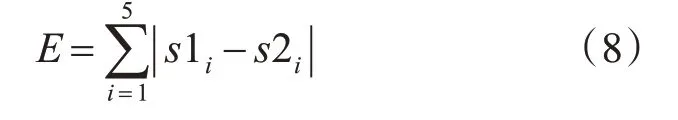
2.2.3 基于指尖向量點積差異度的兩手比較

歐幾里得差異度可表示指尖位置不同的兩手手勢之間的差異，但當指尖位置相同手勢不同時，例如兩只手指彎曲狀態不同，歐幾里得差不能體現兩手之間的差異。因此我們可以進一步通過對標準手和待測手對應的指尖點求向量點積的方法表示兩手之間的差異度。設，i=(1，…，5)，為標準手指尖點的向量，，i=(1，…，5)，為待測手手指指尖點的向量，則向量點積差異度D可表示為式（9），其中，D越小，則表示兩手差異越小。

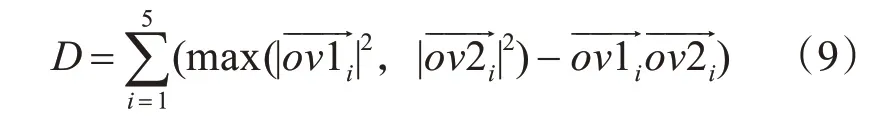
2.2.4 三種比較方法進一步說明

本文采用的三種差異度比較方法體現了患側手和健側手的差異程度。關節點間差異度方法實現簡單，但很多手勢的差異程度不能體現出來。指尖到掌心的歐幾里得距離差異度方法相較關節點間差異度方法做了很大改進，但是當兩手的彎曲狀態不同而指尖位置相同時，歐幾里得差異度視為手勢相同，因此也存在缺陷。本文最后采用的向量點積差異度方法改善了前兩種的缺點。

在現實應用中，可以每種方法單獨使用，也可以結合使用，如下：

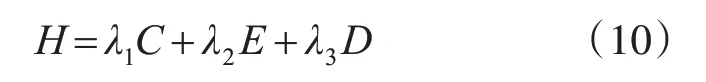
其中λ1，λ2，λ3是各種方法結果的比例因子。

3 實驗與分析

我們的演示系統包括一臺計算機，一個放置雙手的鐵架，以及一個Leap Motion，如圖3所示。

圖3 實驗裝置和實驗過程

為了驗證系統的可行性和運行效果，本文模擬兩種情況進行系統的手勢識別差異的分析。第一種情況是病患的一只手出現問題而另一只手正常，則將患者正常的手作為健側手，出現的問題的手作為患側手，進行差異度檢測并對患側手進行診斷。當病患只有一只手且這只手出現問題時，則是本文模擬的第二種情況，此時病患出問題的手作為患側手，另一個人的正常手作為健側手，即將他人的手作為標準進行差異度檢測并對病患的患側手進行診斷。下面本文分別針對這兩種情況詳細介紹。

3.1 患側手和健側手為同一人的手

共10位受試者分別做出圖4的兩組手勢，第一組手勢旨在研究手指是否彎曲對手勢差異的影響，包括圖4 的（a）和（b），其中（a）請每位受勢者左手和右手都做OK 手勢，（b）請每位受試者左手做OK手勢，右手在OK手勢的基礎上使中指，無名指和小拇指彎曲。第二組手勢旨在研究手指的彎曲程度對手勢差異度的影響，包括圖4 的（c）和（d），其中（c）請每位受試者左手拇指伸直，食指微屈作為標準手，右手拇指伸直，食指伸直；（d）請每位受試者左手手勢不變，將右手拇指伸直，食指彎曲。待系統顯示結果穩定后記錄數據，最后求平均值進行分析。

圖4 實驗手勢

圖5 是實驗平臺顯示界面上手勢變化情況，其中帶有藍色背景的界面是Leap Motion 工作界面，三個參數C，E 和D 體現兩只手整體差異度。C 表示關節點間差異度，E 表示指尖到掌心的歐幾里得距離差異度，D 為向量點積差異度。從圖5 我們可以得知，當兩手手勢相近時，每個參數的值都很小，如圖5（a）所示。反之當兩手部分手指表現不同時，則相應數據變大，如圖5（b）。

圖5 實驗結果

表1 和表2 為10 位受試者做兩組手勢的實驗數據，以每組結果的平均值為依據進行分析。首先分析患者手指是否彎曲對手勢差異結果的影響，如表1（a）所示，當受試者左手和右手都做OK 手勢時，受試者差異值的平均值都很小；而當受試者將右手的中指，無名指和小拇指彎曲時，從（b）的五個手指差異的平均值可看差異值明顯上升說明待測手和標準手差異很明顯。

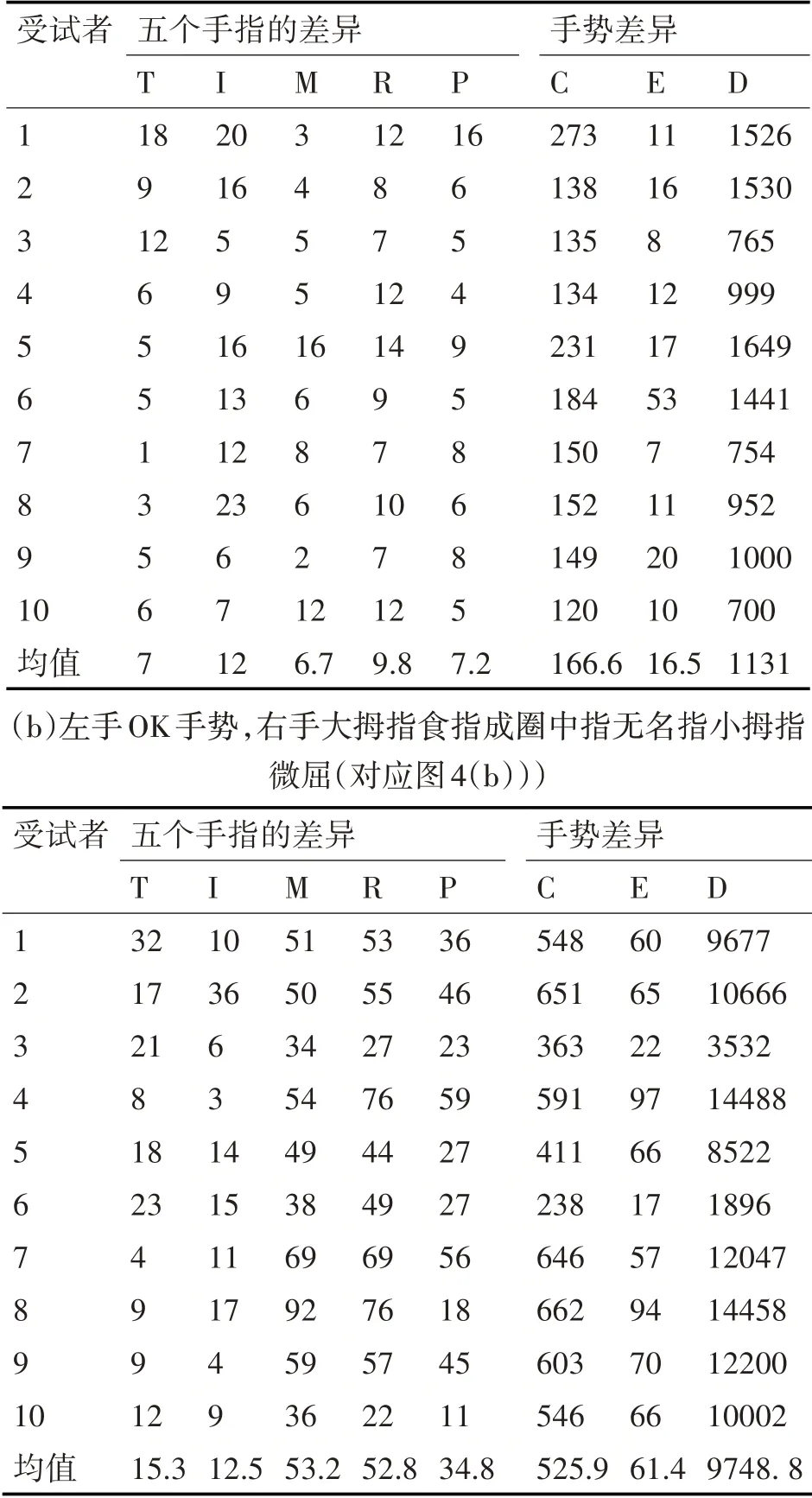
表1 手指是否彎曲對手勢差異結果的影響T=Thumb，I=Index，M=Middle，R=Ring，P=Pink（下同）（a）左手和右手做OK手勢（對應圖4（a）））

當受試者左手大拇指伸直食指微屈，右手大拇指伸直食指伸直時結果如表2（a）所示，Index 平均值明顯高于其它幾個手指說明系統檢測出待測手和標準手的食指之間的差異；當受試者將右手的食指彎曲時，結果如（b）所示，可見Index值明顯上升，且D 的平均值遠高于右手食指伸直的D 值，說明手指的彎曲程度更大時D值更高。

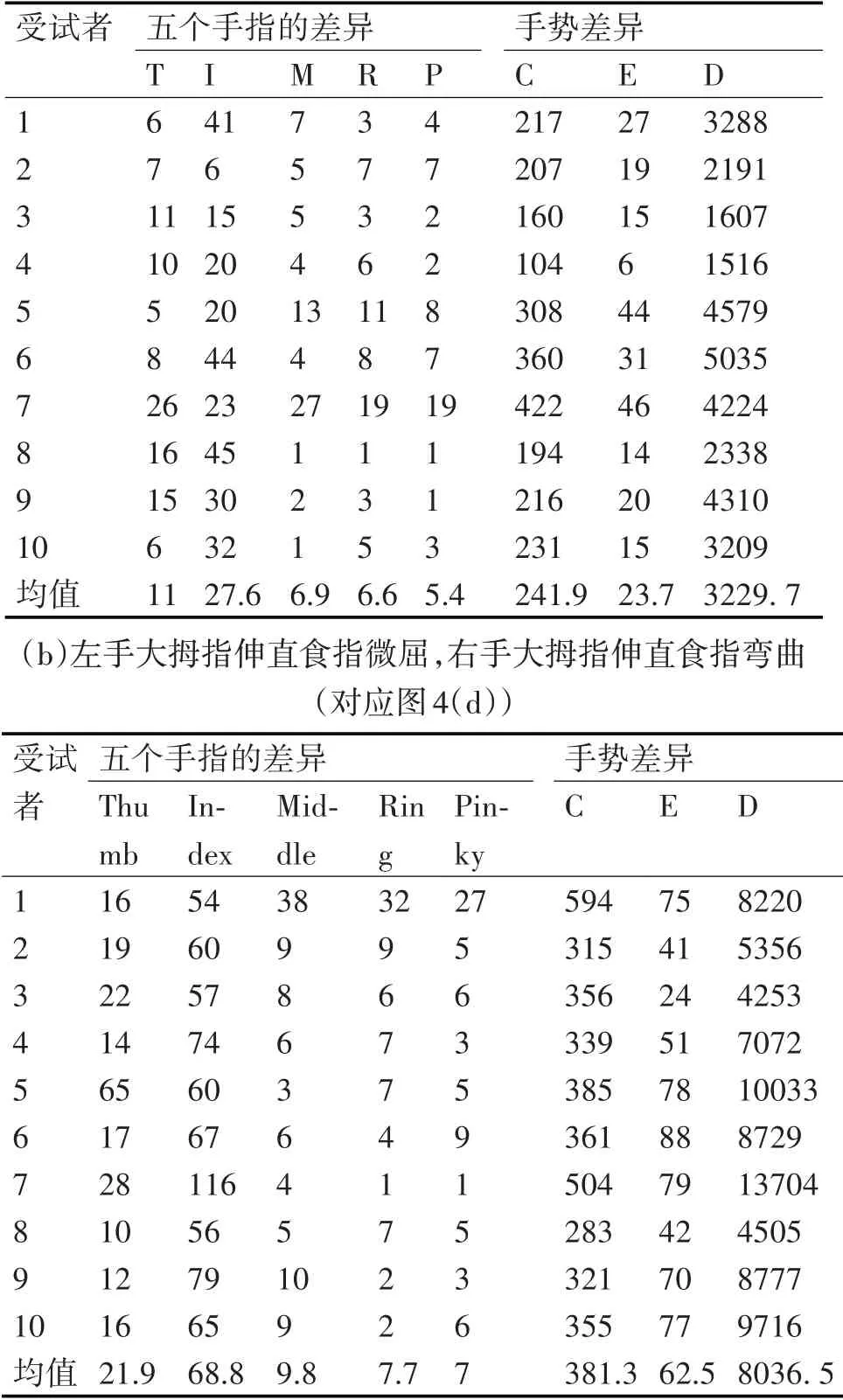
表2 患者手指的彎曲程度對手勢差異結果的影響（a）左手大拇指伸直食指微屈，右手大拇指伸直食指伸直（對應圖4（c））

3.2 患側手和健側手為不同人的手

本文模擬的第二種情況是病患只有一個手且這只手是病患手，則需要將另一個人的正常手作為健側手。我們請10 位受試者兩兩為一組，每組中一個人的左手作為健側手，另一個人的右手為患側手。成員做圖4的（a）和（b）手勢，表3為實驗結果，其顯示說明本系統進行差異度比較時無論以自己的手作為健側手還是以別人的手作為健側手，檢測結果都基本相同。

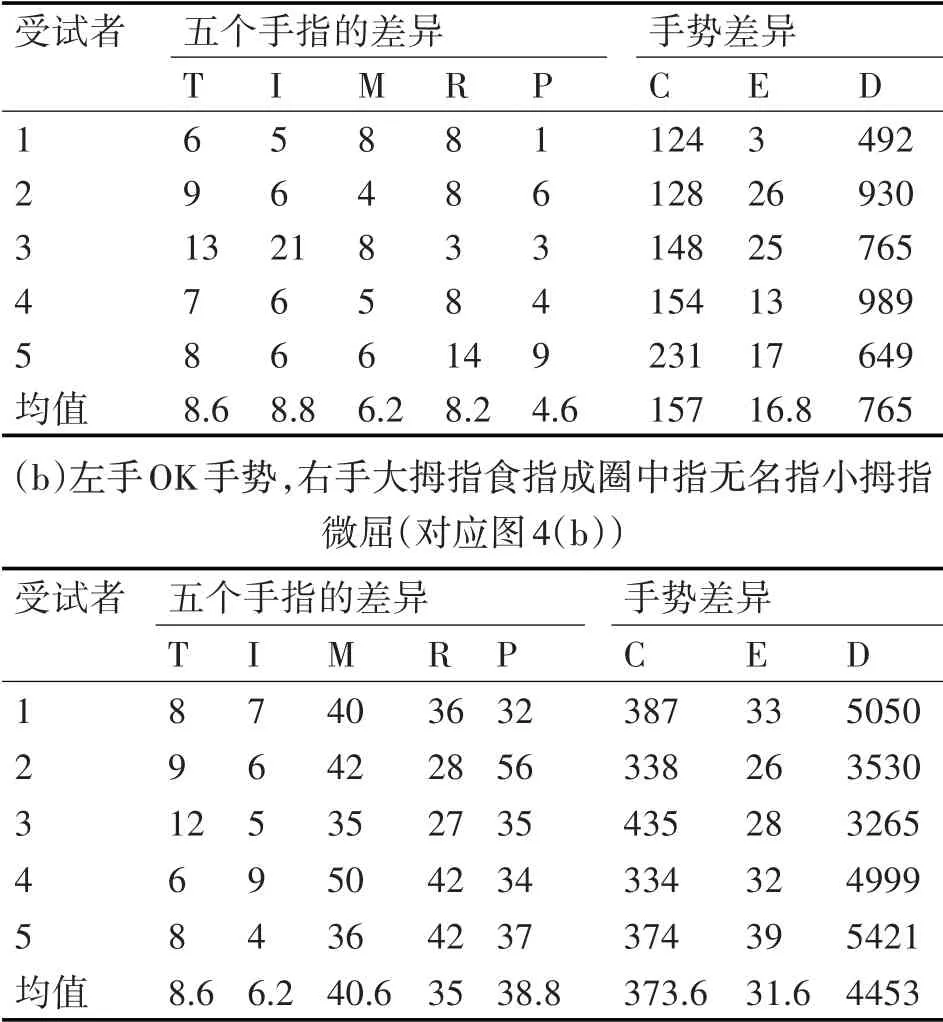
表3 健側手和患側手分屬兩人對實驗結果的影響（a）左手和右做OK手勢（對應圖4（a））

實驗結果表明，在患側手和健側手為同一個人的手的情況下，手指的差異度都能做出較準確的判斷。

4 結語

本文是基于人體交互設備Leap Motion，構建了一個病患手評估系統，該系統通過分析Leap Motion探測并建立的手部模型提取各個部位的特征信息，進而可以判斷兩手的差異程度，可以提供給醫生或者專家作為量化數據的指標以供參考。