基于功率測量的MIMO雷達天線異常檢測方法

張曉冬，唐文明，蔣耿明

(復旦大學信息科學與工程學院，上海 200433)

1 引言

近年來，隨著毫米波雷達理論的發展和器件的成熟，這項技術逐漸在安防、車載雷達等民用領域發揮重要的作用[1]。毫米波雷達的發射波長為1～10mm，頻率分布在30～300GHz。較短的波長使其具備高分辨率的特點和精準的探測能力。根據工作機制，毫米波雷達可分為脈沖體制雷達和連續波體制雷達。其中，調頻連續波(FMCW)是后者的代表之一，它通過連續發射調頻信號來進行測距、測角和測速等工作。

MIMO技術的應用使毫米波雷達的硬件成本降低，其高分辨率的特點得以施展。MIMO雷達通過增加發送天線TX數構建虛擬的天線陣列，以M根TX天線和N根接收天線RX就可達到與M·N根RX天線的單輸入多輸出(SIMO)雷達相同角分辨率的效果。其中，天線作為MIMO毫米波雷達系統中的關鍵模塊，其性能優劣直接決定著系統性能，若天線存在異常，則可能導致天線壽命縮短，系統無法正常工作等結果。針對這一問題很多學者提出一些直接或間接檢測天線異常的方法：文獻[2]實時分析天線通道數據，通過判斷數據是否異常來確定通道的工作狀態，該方法能夠有效定位異常天線，但對于因為電路虛焊等原因導致的天線功率細微損耗所引發的問題則可能出現漏報的情況。

射頻功率計是一種常被用于測量雷達信號功率的裝置，該功率計可以直接測出功率且頻率覆蓋廣，支持的動態測量范圍大[3]，另一種測量功率的方法基于頻譜儀，該方法通過脈沖調制信號的頻譜來獲取平均功率與峰值功率[4]，這些方法雖然提高雷達功率測量精度，但體積和重量都比較大，成本高，且便攜性低，故應用場景受限。若在功率測量方法的基礎上加以改進提出一種更高效的基于簡單電路的方法，則很有可能提高測量的實時性與便攜性。

本文在相關研究基礎上提出一種基于功率的間接檢測天線異常的方法，采用功率芯片TPS259827+CPU實時采集功率信號，結合5/3小波去噪與Hermite包絡插值檢測MIMO毫米波雷達中天線功率的變化，間接測量MIMO毫米波雷達天線異常。Hermite插值作為一種低階分段多項式插值方法很好的解決了高階多項式插值的龍格現象[5]，大大減小了插值誤差[6]，穩定性與收斂性都得到了保證[7]。該功率檢測模塊結構簡單，體積小，成本低，不同于傳統的分離測量器件，可以集成到雷達系統中，具有較高的應用價值。除了對天線的異常監測外，功率測量有助于為雷達系統的硬件設計提供有價值的參考，如供電系統設計、PCB的板材選擇與走線設計等。

2 MIMO毫米波雷達工作機理與功率檢測方案

基于FMCW的MIMO毫米波雷達典型的TDM工作機理如圖1所示，采用通道分離技術，每根TX天線在其對應的時隙中完成從打開到關閉的操作，令RX天線能分辨出不同TX天線對應的信號，使得虛擬陣列的構造成為可能。

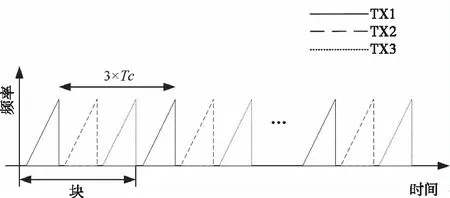
圖1 TDM-MIMO毫米波雷達工作機理[8]

由此可知，通過測量系統電源的功率，可以檢測雷達設備中天線的運行狀況。本文基于系統中天線開啟、關閉時出現的功率跳變的現象提出一種可以偵測跳變沿的功率測量方案，其流程主要包括功率信號采集與去噪、跳變沿監測和插值平滑等步驟。

圖2 功率測量框圖

功率測量框圖如圖2所示，MIMO毫米波雷達系統由12V電源供電，TPS259827芯片提供電源短路與過壓保護等功能，該芯片除輸出電源12V電壓外，還會監視電源的輸入電流。通過GD32F307E單片機讀取該信息并轉換為功率信號。TDM-MIMO雷達天線在發射和切換時都會引起功率的變化，由此可以監視天線的運作狀態。最后，功率信號經信號處理模塊濾除噪聲的干擾，得到更為精確的天線發射功率測量與異常檢測結果。

3 功率信號處理

3.1 信號預處理

系統中功率信號的采集由單片機執行，采集到的電源功率信號不可避免的存在噪聲，目前時間序列降噪效果較好的方法有自適應濾波[9]和小波閾值技術[10]等。其中小波變換在時域和頻域都有很好的局部化特征，這有助于分析和處理非平穩信號[11]。5/3提升小波簡化了傳統小波變換的運算過程，在運算資源不充裕的情況下大大提高了算法的運行速度，能夠很好的解決因為數據未及時處理引起的數據擁塞問題。

相比于之前基于Mallat算法的快速小波變換，5/3提升小波不依賴于傅里葉變換，從而消除大量復雜的卷積運算，大幅提升了運算速度。

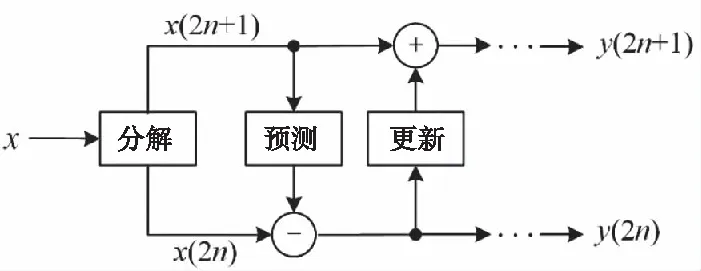
圖3 提升小波變換

提升小波變換包括了分解、預測和更新三步驟[12]，其流程如圖3所示。數據序列x首先分解為偶數序列和奇數序列子集，偶數序列經預測過程后逼近奇數序列，其與奇數序列差值后得到高頻分量H；H經過更新后生成相應的低頻分量L，其算法描述如式(1)所示，只需要經過簡單的加減和除法運算就可以實現傳統小波變換的復雜過程。

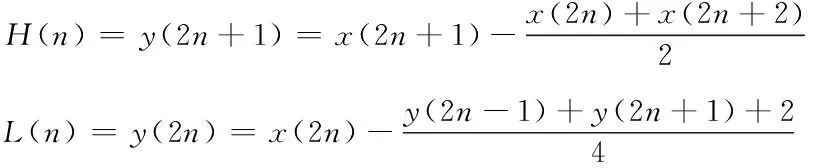
(1)

經過小波變換后，含有噪聲的功率信號分解成多尺度下的小波系數。根據一般情況下噪聲小波系數幅值小于信號小波系數幅值這一特性，選擇合適的閾值對噪聲進行消除。由于功率信號中的噪聲基本分布在信號的高頻部分，因此保留低頻分量，只對高頻分量進行閾值處理。

閾值T的選取很大程度上取決于噪聲的分布情況，這對去噪的效果有著極大的影響。隨著分解層數的加深，由深層的低頻分量分解出的高頻系數中，噪聲的成分將變得很小，其對閾值選取參考的貢獻也將不大，因此本文只將第一層的小波系數作為考量，根據式(2)計算閾值T，其中σ為小波系數的標準差，n為系數個數。

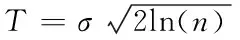
(2)

常用的兩種閾值處理策略是Donoho提出的軟閾值和硬閾值函數[13]。信號在軟閾值處理前后的幅值將會收縮且難以恢復，這使得測量值產生失真。而硬閾值則會保留大于閾值的小波系數，重構后功率幅值得到很好的保留。因此本文選擇硬閾值策略，圖4為對信號進行兩層小波分解后的閾值去噪流程。

圖4 2層小波分解

為了從分解后的小波系數中恢復出噪聲消除后的信號，需要執行小波重構，小波重構就是小波逆變換過程，包括反更新、反預測和反合并三步驟[12]，其流程恰為圖3的逆過程。經過小波閾值去噪的信號和原始信號的對比如圖5所示。

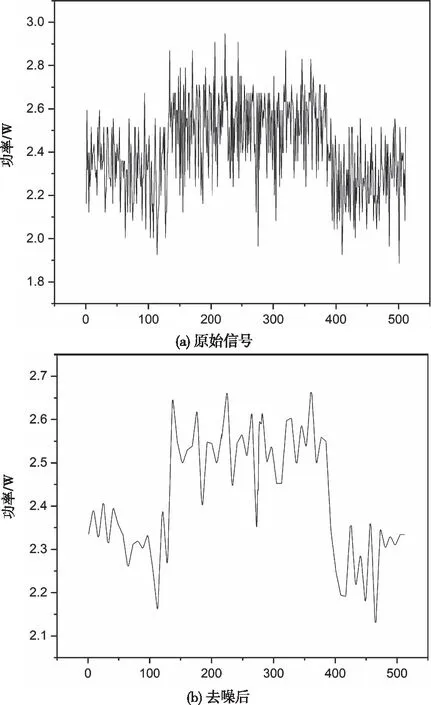
圖5 去噪前后功率信號

3.2 信號估計處理

采用Hermite插值法對信號的包絡進行軟件重采樣以提高采樣率，然后對插值后的上下包絡取平均，能有效提高信號的分辨率與對真實信號的估計。

3.2.1 Hermite包絡插值

本文采用的兩點三次Hermite樣條插值在傳統的Hermite插值[14]基礎上做了簡化，提高了運算效率。其算法如下：對函數y=f(x)在節點xi和xi+1的數據進行插值，在給定兩個插值點的函數值y(x)和一階導函數g(x)的條件下，即可計算出插值函數。

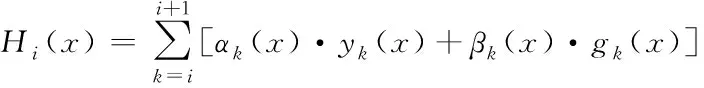
(3)

其中αk(x)、βk(x)均為插值基函數。

從圖5(b)可以看出經過去噪后的信號仍然存在較大的抖動，若對此信號直接插值，則結果必然會導致最終的讀數仍存在較大幅度的抖動。為了平滑數據抖動，本文首先取信號的上下峰值點，再基于這些點進行插值，得到插值后的上下包絡。最后，將插值后的上下包絡平均作為結果。

圖6 包絡插值

在進行Hermite插值時，數據的一階導信息無法預知，本文采用簡單的三點差分法來近似包絡E(n)插值點處的一階導數值。

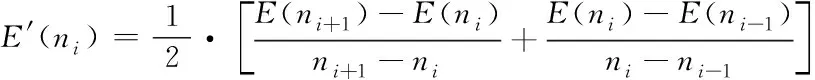
(4)

插值后，數據點的增加豐富了功率信號的細節信息。接著將兩條包絡曲線作平均，得到如圖7所示平滑后數據的結果。

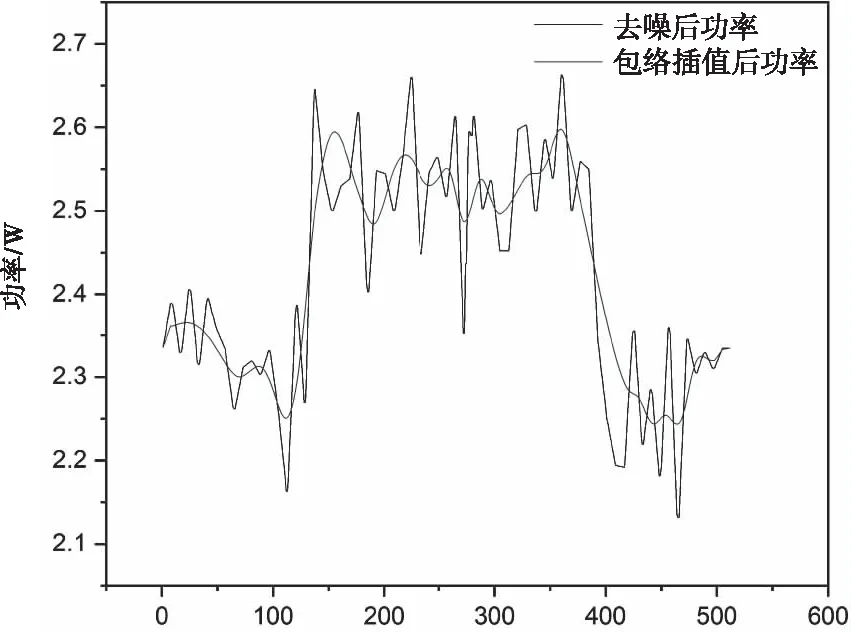
圖7 上下包絡平均

可以看到，數據得到了極大的平滑，曲線過渡自然，波動也不再劇烈。但與此同時，跳變沿處的數據也被同步平滑，此處的曲線較原信號更加平坦，產生失真。針對這一問題，本文通過偵測跳邊沿來避免信號的失真。

3.3 功率跳變偵測

為了避免在平滑信號波動時，功率跳變沿被同時平滑，對輸入的信號進行跳變沿檢測，若存在則對此段數據作特殊處理。以下的方法原理簡單，計算復雜度低，但能有效的定位跳變沿。

3.3.1 數值變化趨勢計算

如果對插值后數據量大幅增加的信號進行處理，則會加重硬件的計算負擔，因此本文在插值前即開始檢測功率的跳變。

觀測到圖5(b)在跳變沿處的數據有2個特點：功率幅度變化最大，跳變時間極短。考慮到去噪后殘留的噪聲幅值一般都是小于功率跳變幅度，因此計算出一段數據不同時間段內的功率變化值，若該段數據中存在跳變沿則必然存在于變化值最大所對應的那個時間段內。

在未做任何平滑的情況下利用簡單的滑動窗口平均法可以稀釋數據量，減少殘留噪聲的影響。

(5)

其中，k為滑動窗口的大小。接著，對數據采用式(6)所示的前向差分，計算出信號的變化差值隨時間的變化情況。其中，d為差分間隔。

delta(m) =w(m+d)-w(m)m=1，2，…

(6)

將以上的算法應用于存在兩個跳變沿的圖5(b)信號中，結果如圖8所示。該圖很明顯的存在兩個尖峰，且幅度遠大于其它峰值，不難推斷，位于左邊的尖峰對應著功率的上升沿，而右邊的則對應下降沿。由此可以根據峰值的大小判斷數據中是否存在跳變。

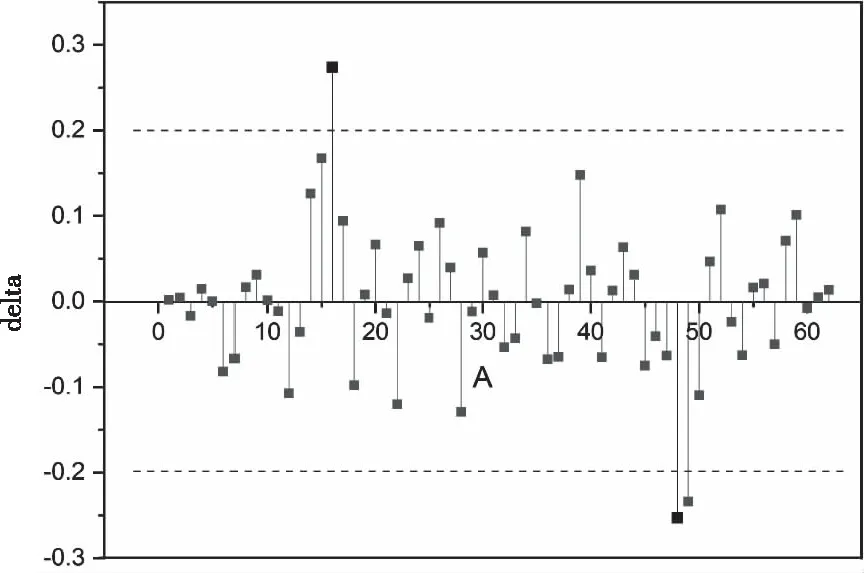
圖8 數據變化趨勢

3.3.2 跳變點定位

由于經過滑動窗口平均，圖8中的每一個點都對應著信號中的一段區間，為了準確定位功率的跳變點，采用最小二乘估計法(LSE)對位置進行估計。

以圖8為例，若左邊尖峰所包含的數據點為Xi，定義待估參數為XOPT，算法描述如下

(7)

求解上式可得

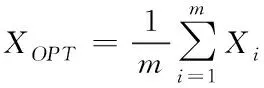
(8)

由于信號的數據點間隔相同，上式可化簡為

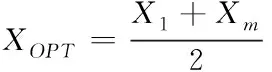
(9)

根據式(9)所求得的XOPT即為功率的跳變點，結合確定跳邊沿長度的先驗條件，確定跳變區間。

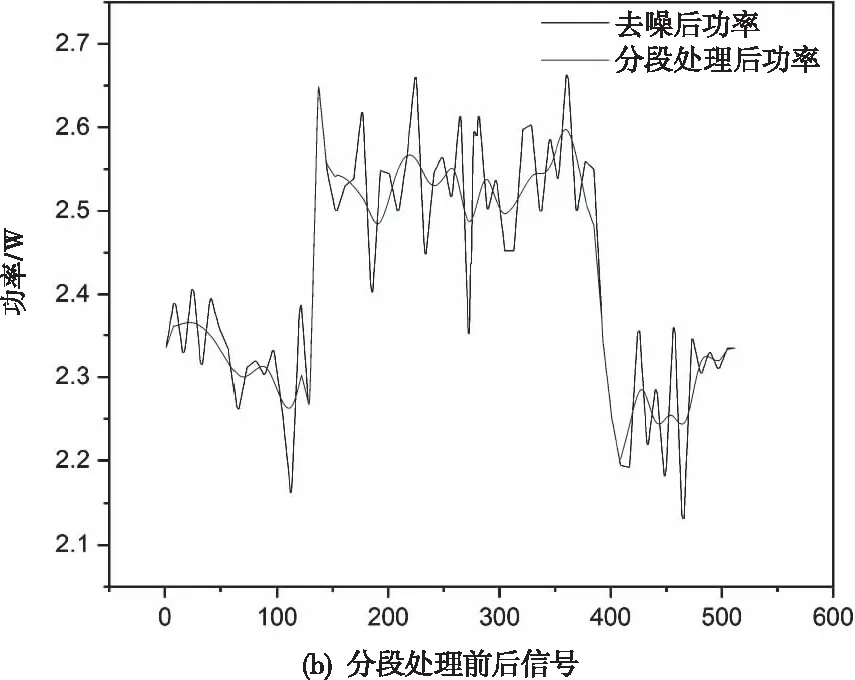
圖9 定位功率跳變沿分段處理

觀察到上升沿和下降沿處的信號并不存在明顯的抖動，對處在跳變區間的數據進行單一插值，而對其它數據就采用包絡插值平均處理，分段處理后的結果如上圖所示。

4 系統測試與實驗結果

本文的測試平臺為自主研發的雷達信號處理板卡，該板卡載有四片包含3發4收天線的AWR1243芯片，可以實現雷達信號的定時發送和接收，配置芯片調頻連續波參數等功能。除此之外，板上集成了GD32F307E單片機與功率測量芯片，單片機通過ADC接口讀取系統的電源功率。

圖10 MIMO雷達天線評估實驗裝置圖

表1 MIMO雷達天線評估實驗參數表

配置雷達信號處理板卡，開啟所有天線，表1為實驗的設置參數。天線以時分復用的方式輪詢發射，采集到的電源功率信號如圖11(a)所示。應用本文的算法對信號進行處理，得到的最終結果如圖11(b)所示。從實驗結果看出，在12根發射天線中，有3根天線的發射功率小于其它天線(按從左至右的順序記為天線7、8、9)，相比于原始功率信號，在經過算法處理后，該異常現象更加明顯。經計算驗證，算法處理前后，3根異常天線與其它正常天線發射時的功率信號方差比如表2所示，處理后的方差比分別下降了7.57%、9.50%和8.60%，表明本文的算法有效地放大了數據中異常天線與正常天線之間的差異性。

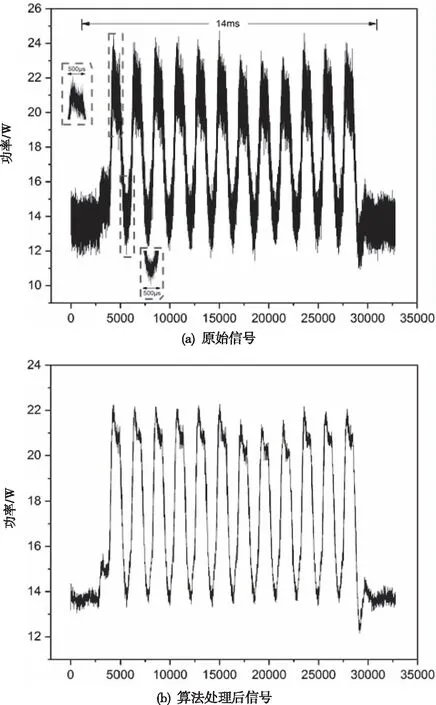
圖11 雷達開啟前后的系統電源功率

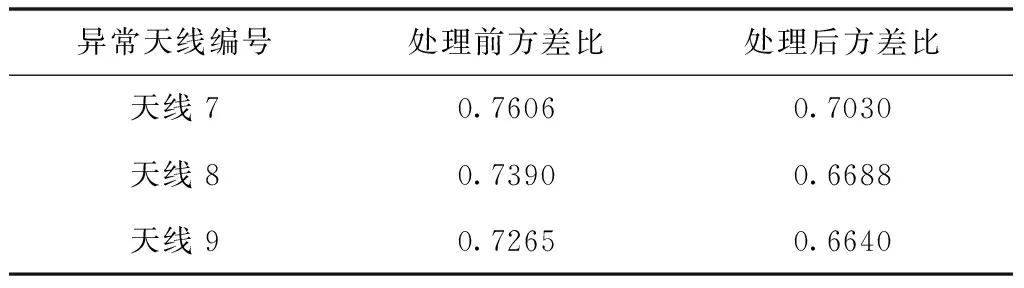
表2 算法處理前后異常天線與正常天線的功率信號方差比(平均值)

5 結論

本文提出的基于功率測量的MIMO毫米波雷達天線異常檢測法，利用單片機+功率芯片讀取系統電源功率，并對讀取到的信號采用如下方案：

1) 預處理：利用5/3提升小波閾值法對信號進行去噪；

2) 包絡處理：對信號取上下包絡并求均值以平滑數據的波動；

3) 功率跳變沿偵測：利用滑窗差分評估數據的變化趨勢以判斷數據段中是否存在跳變沿，并結合最小二乘法精確定位跳變點。

能有效測量出MIMO毫米波雷達天線功率實時變化值，可以直觀地獲取各天線發射所消耗的功率，天線開啟、關閉的時間和天線間的均勻性等信息，間接對各天線性能進行有效評估，具有方法靈活、結構簡單的特點。實驗結果表明，本文的測量方法在對天線異常檢測的場景中具有良好的實際應用效果，具有推廣作用，可以應用于其它的如供電模塊檢測、過流保護等系統。