冗余無線傳感網絡的最小成本部署問題
史文武,王 然
(杭州電子科技大學,浙江 杭州 310018)
0 引言
無線傳感器網絡(Wireless Sensor Networks,WSN)被廣泛用于對自然環境[1]和基礎設施[2]的長期監視,因此,WSN的存活時間是一項重要指標。降低WSN的能量消耗速率或為WSN提供額外的能量,都能提高WSN的存活壽命,然而通過控制數據路由和加入睡眠/喚醒機制降低WSN的能量消耗速率的方式,只能有限延長WSN的壽命。為了讓WSN永久運行,現有文獻主要從兩種途徑來實現:
(1)通過收集不穩定的自然環境中的能量,如太陽能、風能等[3-5];
(2)通過穩定的無線能量傳輸(Wireless Energy Transfer,WET)[6,7]。
然而,由于來自環境的能量通常很難預測[6],這會使WSN的監視性能隨時間的推移而不穩定。
WET使用專用的能量基站(energy Base Stations,eBS)為無線設備遠程充電[8],由eBS供電的WSN稱為無線供電的傳感器網絡(Wirelessly Powered Sensor Networks,WPSN)。通過穩定的無線能量傳輸,能更好地控制WPSN中的傳感器節點的能量獲取[9]。通過載有無線充電源的可移動載具,按照規劃的路徑給傳感器節點充電是一種常用方法[10-12],但某些野外場景(如森林、山坡)并不適合載具的移動。Du等人[13]通過在網絡中部署冗余節點,利用能量波束成形技術[14],位置固定的eBS同時向同一區域內彼此靠近的節點充電,使該區域單位時間內獲取更多的能量,同時每個節點可以通過休眠/喚醒機制消耗更少的能量來滿足監視需求。這些節點可以通過輪流工作來節省能源,這解決了單eBS情況下聯合節點部署和無線能量傳輸調度問題。
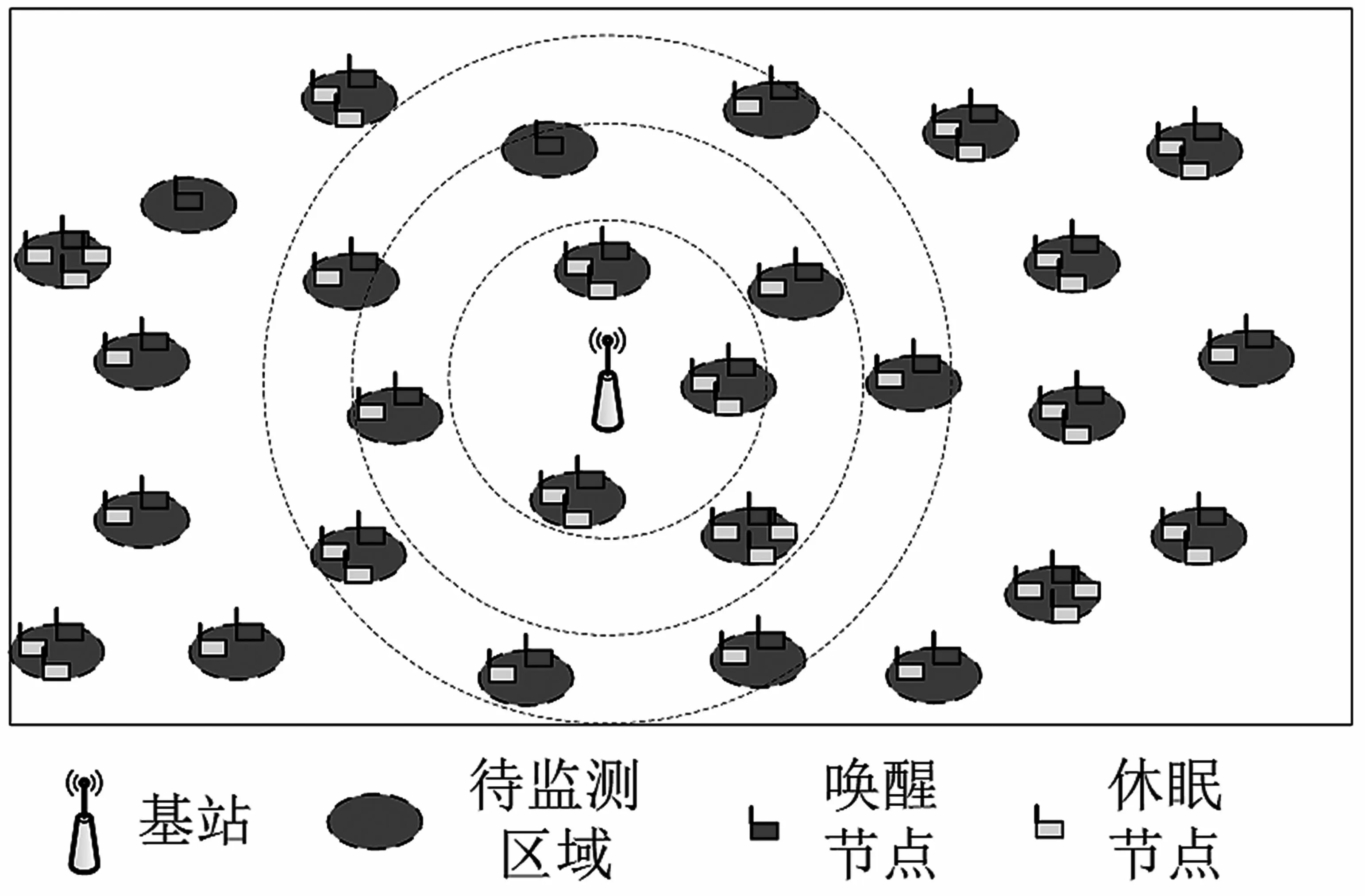
現實情況下,單eBS覆蓋范圍有限,如何在給定待監測的感興趣區域的條件下聯合確定基站位置和傳感器數量,使WPSN在成本最低的情況下保持持續不斷地監測是一個重要問題。考慮如圖1所示的WPSN,有多個感興趣的區域要用傳感器節點進行監視。eBS將能量傳輸到傳感器節點以監測環境并上傳測量結果。當eBS向某一區域傳輸能量時,該區域中部署的多個傳感器節點可以同時收集能量,并且輪流工作以減少能耗。因此,自然會產生以下問題:
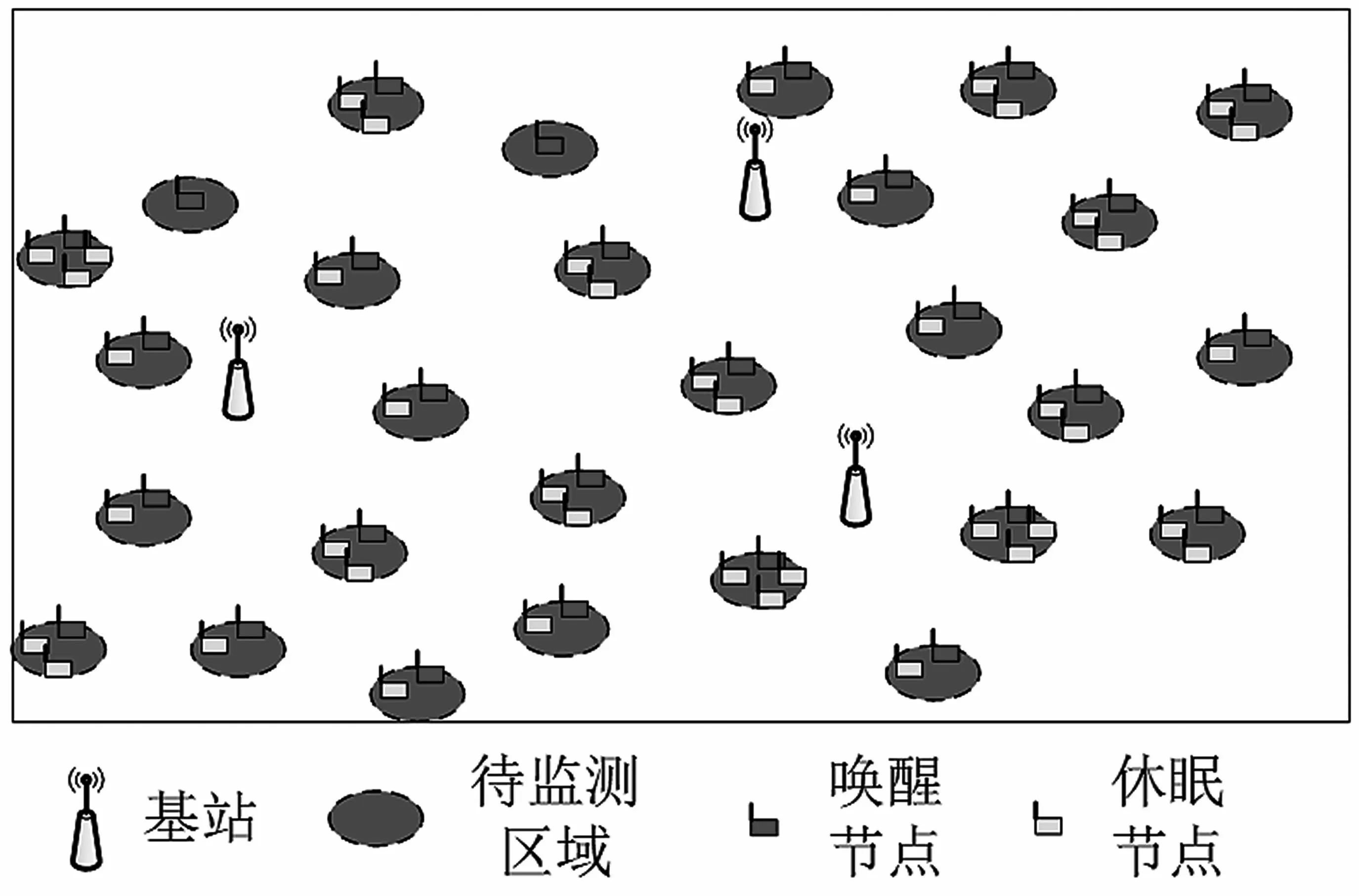
圖1 網絡模型
(1)傳感器節點的部署數量;
(2)基站的部署數量和位置;
(3)WET調度,即每個eBS某時刻應向哪個區域傳輸能量。
該問題把傳感器數量選擇和基站的數量、位置部署以及WET調度結合在一起,在保證網絡持久運行的前提下,最小化傳感器和基站的聯合成本。
為解決此問題,本文在該問題上添加約束,令待監測區域僅被固定的某一基站充電,以簡化充電問題,并設計基站最佳覆蓋范圍搜索算法解耦了傳感器部署和基站部署問題,最后用迭代算法求解基站的部署位置,得到簡化問題的解,并將其作為原問題的近似解決方案。
1 問題定義
在本節中,首先介紹所采用的網絡模型和無線充電模型,其次正式給出優化問題的形式定義及相關的約束條件。
1.1 網絡模型
如圖1中所示的WPSN模型,二維平面內有N個待監測的感興趣區域,區域間有一定的距離,單個區域中的節點彼此靠近。eBS通過無線方式為傳感器節點提供能量,并從節點收集數據。由于能量是由RF承載的,因此會遭受較高的路徑損耗。從而,eBS使用能量波束成形將能量集中到目標[15]。每個傳感器節點都使用整流天線從eBS收集RF能量,并將能量存儲到其可充電電池中。
本文使用{li},i=1,2,…,N表示N個待監視區域。在每個區域li中,部署了xi個傳感器節點,x=[x1,x2,…,xN]T表示每個區域的傳感器節點數量。{bm},m=1,2,…,M用來表示M個eBS,W=((u1,v1),(u2,v2),…,(uM,vM))T表示每個eBS的坐標。本文希望找到W和x的最佳值,在確保WPSN監視性能的同時最小化部署網絡所需成本。部署節點后,WPSN開始進行監測。把時間劃分為多個時隙,每個時隙包含能量傳輸和數據傳輸兩個階段。
1.2 能量傳輸階段
在能量傳輸階段,eBS會形成尖銳的能量束,以對某個區域中的節點充電。令0-1變量ym(t)=(ym1(t),ym2(t),…,ymn(t))T表示在時隙t時,基站bm的充電調度方案,如果基站bm將能量傳輸到區域li,則ymi(t)=1,否則ymi(t)=0。令P表示eBS的發射功率。在允許在同一區域中部署多個節點的情況下,該區域中的所有傳感器節點都可以同時收集RF能量,且接收功率相同。而其他區域中的節點則無法收集。當基站bm向區域li傳輸能量時,可以用項αmi來表示充電功率:
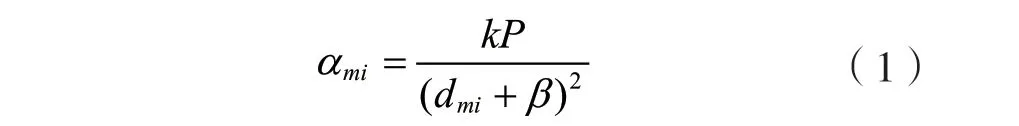
除αmi以外,區域li處的節點的接收功率還取決于li處的傳感器節點數,一個原因是,在li節點較少的情況下,eBS可以使用更集中的波束來覆蓋li的所有節點;另一個原因是,當部署更多節點時,節點間更有可能存在能量束的遮蔽效應。因此,本文使用節點數g(xi)的函數來表示由于節點部署而造成的這種損失[13]。那么,區域li中的節點單位時間所收集的總能量為αmig(xi)ymi(t)。本文假設這些節點平均共享總能量,即節點平均收獲功率為αmig(xi)ymi(t)/xi。g(xi)具有以下特性:g(1)=1且0≤g′(xi)<1,對于所有大于或等于1的xi,g′(xi)≤0,g(1)=1為基準。第二個假設0≤g′(xi)≤1,g′(xi)≤0是因為遮蔽效應,隨著節點的增加,總收獲的能量在增加,但收益是遞減的。區域中的節點收集的總能量不能大于傳輸的能量,即g(xi)應該是有界的。基于上述假設,g(xi)/xi是相對于xi單調遞減的。這意味著,隨著在同一區域中部署更多的節點,每個傳感器節點收集到的能量都將減少。函數g(x)的性質如圖2所示。
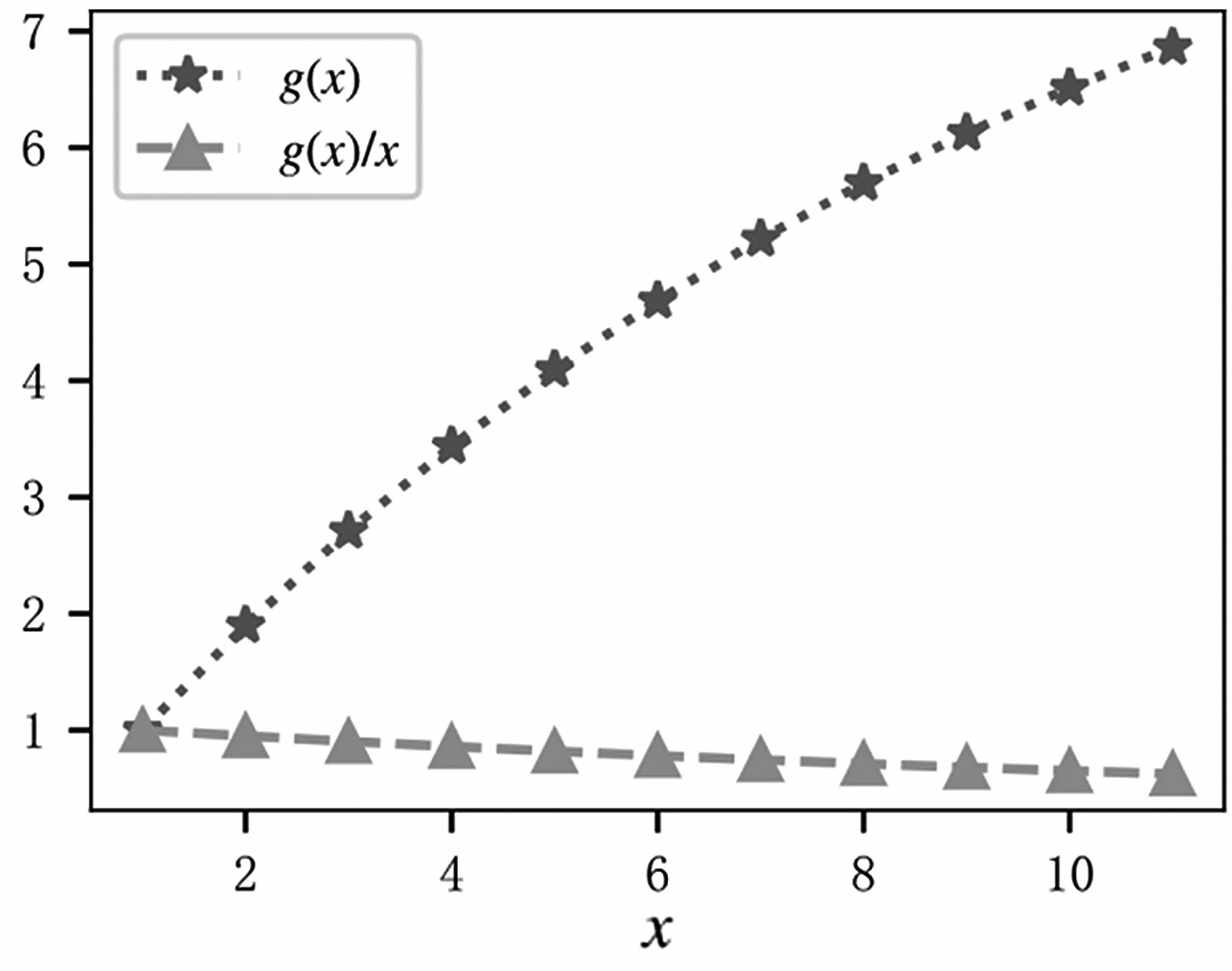
圖2 函數g(x)的性質
1.3 數據傳輸階段
在數據傳輸階段,同一區域的傳感器節點應用休眠/喚醒機制節省能量。更具體地,在時隙t中,每個區域有且僅有一個節點被喚醒,監測環境并發送數據,而其他節點處于休眠狀態。vij表示區域li中的第j個節點。zi(t)=(zi1(t),zi2(t),…,zixi(t))T表示在時隙t中區域li內的節點的激活調度,其中0-1變量zij(t)是vij在時隙t的狀態。假設監視應用程序要求區域li的采樣率為λi,則li中節點的能量消耗為cizij(t)+c,其中ci為傳輸λi數據量所花費的能量,c為傳感器的靜態能耗。設Eij(t)為節點vij的剩余能量,所有節點的電池大小為B,時隙長度為D,則傳感器節點的動態能量方程為:
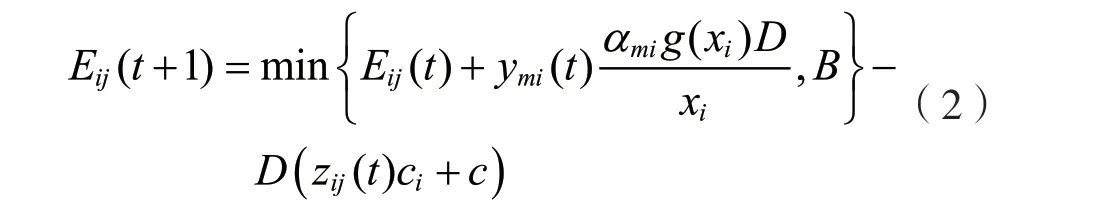
本文假設電池容量很大,即B>>ci,這意味著傳感器節點在幾個時隙中都不會很快耗盡能量。總而言之,可以將WPSN建模為元組(L,c,A,W,x,Y,Z,E,B,D,g),其中L=[li]=[(ui,vi)],c=[c,c1,c2,…,cN],A=[αmi],W=[(u′m,v′m)],x=[xi],Y=[ymi(t)],Z=[zij(t)],E=[Eij(t)]。
1.4 形式化定義
對于給定的無線充電傳感網絡WPSN(L,c,A,W,x,Y,Z,E,B,D,g),在任意時刻,需要所有區域的采樣速率滿足給定要求,否則認為傳感網失效,由此可以給出網絡壽命及優化問題的定義。
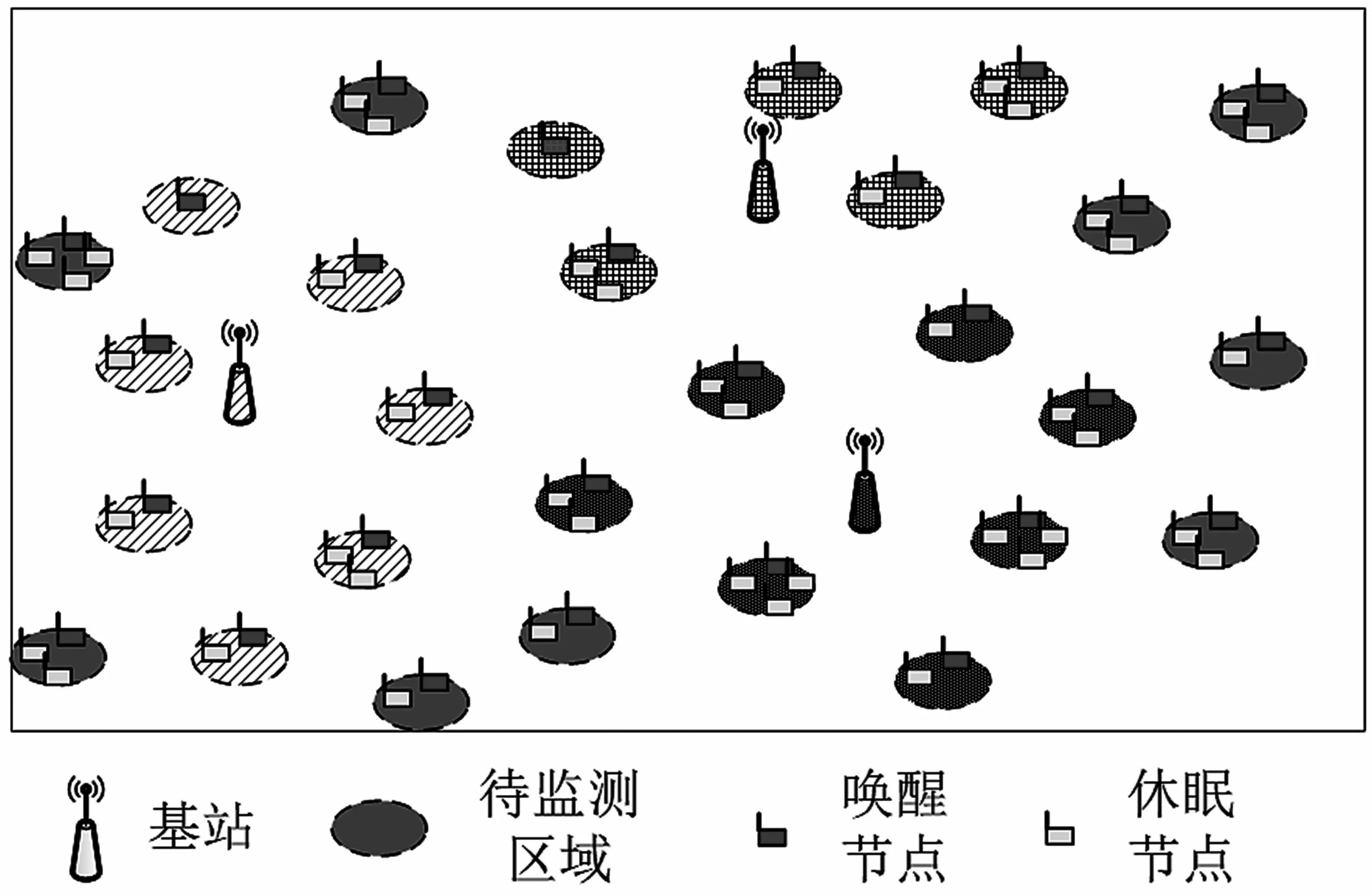
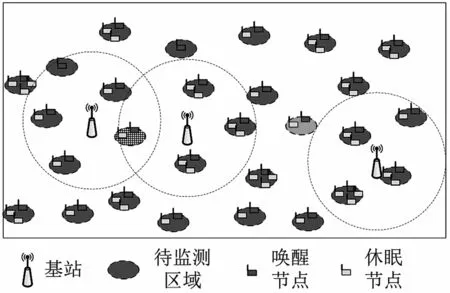
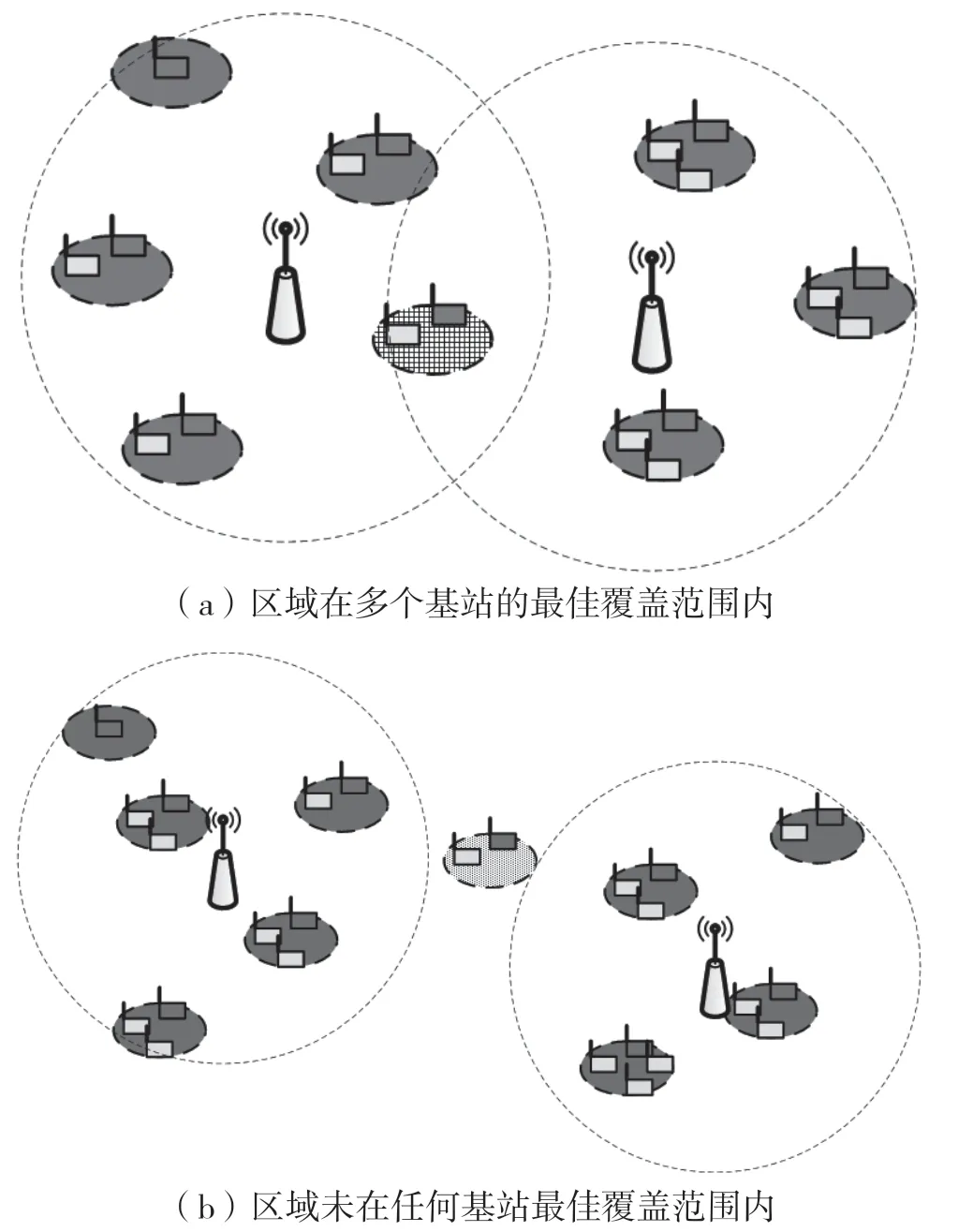
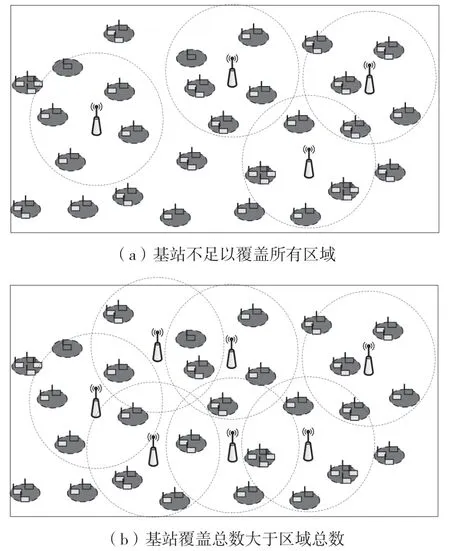
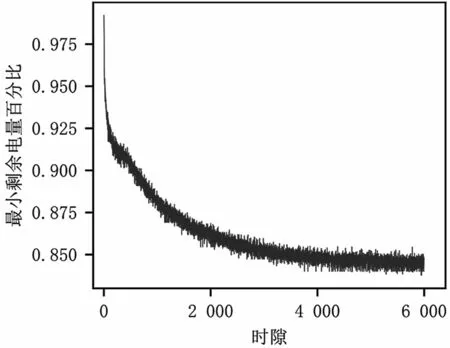
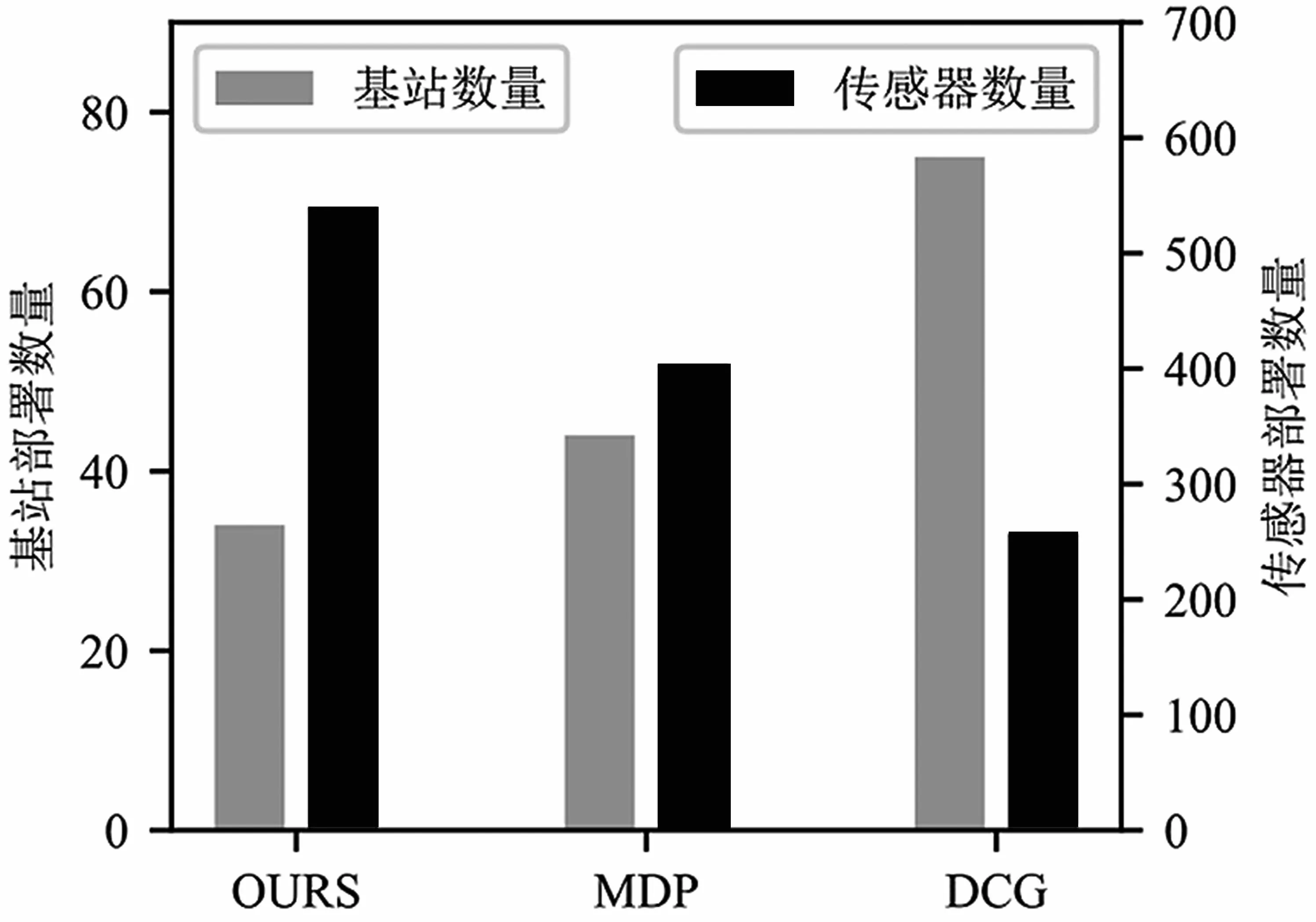
(1)定義1:無線充電傳感網絡的壽命。無線充電傳感網絡WPSN(L,c,A,W,x,Y,Z,E,B,D,g)是可永久運行的,當且僅當在任何時隙t和任何區域li中的任意傳感器節點的剩余能量都是非負的,即Eij(t)≥0。相應地,WPSN(L,c,A,W,x,Y,Z,E,B,D,g)的壽命被定義為首次存在一個傳感器節點,其Eij(t+1) (2)定義2:基于冗余傳感器節點的最小成本部署問題。聯合傳感器部署、節點部署和WET調度問題是找到W,x,Y,Z,使服從WPSN可永久運行的約束下,最小化總部署成本。令ps,pB分別表示單個傳感器節點和eBS的部署成本,根據前文定義,可將問題1表述如下: 其中,式(3)意味著最大限度地降低基站和節點的總成本;約束(4)表示所有節點都不應耗盡能量;約束(7)表示每個eBS在每個時隙中能且只能為一個區域的傳感器節點充電;約束(8)表示對于每個時隙中,每個區域有且只有一個節點工作。 解決問題1的困難,不僅在于整數和0-1約束決策變量,還在于基站部署、傳感器節點部署以及WET調度三者之間存在耦合性。為了解決問題1,本文提出了一個約束條件,得以解耦WET調度,得到簡化的問題,使本文可以更多地關注基站和傳感器節點的部署。 如圖3所示,本文讓每個待監測區域能且只能被某一固定的基站充電。 圖3 網絡模型 令s=(s1,s2,…,sN)T,其中si=1,2,…,M,si=m表示區域li歸屬于基站bm。則問題1可改寫為問題2: 其中,約束(16)中的I(si=m)為指示函數,si=m時結果為1,否則為0。 定理1:區域li應歸屬于距離其最近的基站,即: 證明:如圖3所示,為滿足問題2約束的按距離劃分歸屬的一種解決方案,同一填充樣式的區域屬于相同的基站。不失一般性地,設某一區域l1屬于基站b1,則每個時隙D內,區域l1接收到的總能量為α11g(x1)D,若保持其他條件(傳感器節點部署數量)不變,改變區域l1的歸屬,使其歸屬于b2,則時隙D內區域l1的總接收能量為α21g(x1)D。由d11 基站的最佳覆蓋范圍如圖4所示。對于給定的單個基站的位置和其要覆蓋的區域l1,l2,…,lC,可以計算c和α,并根據基于貪婪的部署(Greedy Based Deployment,GBD)算法[13]計算x=(x1,x2,…,xN)T,使∑x最小。對于同一位置的基站,當覆蓋不同數量的區域時,隨著覆蓋區域數量的增加,更多的區域平攤基站成本,因此每個區域的充電時間占比將會減少。為滿足電量消耗需求,需要在每個區域部署更多的傳感器,這會增加傳感器部署的成本。如圖4,若如最小的圓所示,僅覆蓋3個區域,則可能有x=(1,1,1)T;若如中等大小的圓所示,覆蓋7個區域,則可能有x=(1,2,3,2,3,3,4)T;若如最大的圓所示,基站覆蓋13個區域,則可能有x=(3,4,4,4,5,4,6,5,7,7,8,9,9)T。若傳感器成本與基站成本為1∶15,則3種情況下的每個區域平均成本分別為6,33/7和75/13,則在這3種情況下,覆蓋中等大小的圓時,每個區域的平均成本最小。 圖4 基站的最佳覆蓋范圍 那么,當給定待監測區域坐標L=[l1,l2,…,lN]=[(u1,v1),(u2,v2),…,(uN,vN)]和基站的坐標w=(u,v)時,如何求解基站覆蓋范圍,能使每個區域的平均成本最低?對于此問題,本文設計了基站最佳覆蓋范圍搜索算法,得出最優覆蓋范圍C。 本節的目標是基于定理1和基站最佳覆蓋范圍搜索算法,提出一種迭代式算法,得到問題2的近似解。 圖5展示了迭代過程中可能出現的基站部署位置不合理的典型情況。如圖5所示,對于3個基站的當前位置,虛線圈為各基站的最佳覆蓋范圍。顯然,左邊的基站與中間的基站有覆蓋范圍的重合。根據定理1,每個區域僅歸屬于距離其最近的基站,被重復覆蓋的網格填充區域實際屬于左邊的基站,則中間的基站實際上僅為其余3個區域充電,基站的覆蓋能力未充分利用,徒增了成本。中間基站與右邊基站中間的點狀填充區域未被任何一個基站覆蓋,根據定理1,該區域實際需要被右側的基站覆蓋。這超出了右側基站的最佳覆蓋能力,需要為其覆蓋的所有區域部署更多的傳感器,以使基站對各區域的充電效能更高。圖6列出了迭代過程中可能出現的情況。 圖5 迭代過程局部 圖6 區域視角的迭代情況 如圖6(a)所示,某一區域li在多個基站(n個基站的最佳覆蓋范圍內,則除距離該區域最近的基站外,其余基站應遠離該區域,表達式為: 式中:(ui,vi)為區域li的坐標;lr為步長;I為指示函數,即當i≠j時I為1,否則I為0。 對于情況6(b),某一區域li不在任何基站的最佳覆蓋范圍內,則該區域最鄰近的η(η為可調參數)個基站應該靠近該區域,表達式為: 圖7所示的整體情況中,如圖7(a),顯然所有基站的最佳覆蓋范圍內區域的總和遠小于待監測區域總數。此時,若按就近原則分配區域,會導致部分基站被分配過多的區域,使部署傳感器節點的成本增加,甚至永遠無法滿足充電需求,對于這種情況,需要增添新的基站。如圖7(b)所示,所有基站的最佳覆蓋范圍內區域的總和大于待監測區域總數。此時,每個基站分配到的區域數小于最佳覆蓋范圍,導致基站成本未被充分均攤。對于這種情況,需要刪除多余的基站。總體而言,迭代過程中,要保持所有基站的最佳覆蓋范圍內區域的總和與待監測區域總數大致相等。 圖7 總體視角的迭代情況 根據上述區域視角和總體視角中提出的4種情況,迭代算法的具體步驟由算法2給出。 在這一節中將進行大量的仿真實驗,首先針對提出的算法從動態最小剩余電量、基站和傳感器成本比、采樣率、待監測區域數等方面進行評估;其次與貪心策略進行對比。實驗結果證實了本文算法的優越性。 WPSN由N個部署傳感器的待監測區域和M個未知位置的待部署基站組成。默認情況下的網絡參數設置:250個待監測區域隨機位于長、寬均為300 m的方形范圍內。部署好的基站可向外發射RF能量,并帶有915 MHz的能量載波。每個區域li的采樣率λi服從[25,30]bits/s的均勻分布。單位比特的傳輸能耗為10-6J/bit,則有ci=10-6λi。傳感器節點的靜態功耗為c=10-6J/s。函數g(x)設置為g(x)=(1-qx)/(1-q),其中q=0.9。基站和傳感器的部署成本比r為25。 3.2.1 模擬充放電過程 首先,對于算法給出的WPSN部署,模擬傳感器耗電感知環境和基站充電過程,并基于等式(1)更新傳感器節點的剩余能量。在每個時隙,記錄下所有傳感器的最小剩余能量百分比。圖8為最小剩余能量百分比的動態。可以看到,在6 000個時隙內,沒有任何一個傳感器節點耗盡其電池能量,并且剩余能量的最小百分比保持在80%以上。通過此算法進行基站和傳感器節點部署,可使WPSN保持持續不斷地監測。 圖8 所有節點的最小剩余電量動態 為檢查算法給出的解決方案相對于節點的消耗功率和采集功率的變化是否具有魯棒性,在節點的消耗功率和采集功率上添加噪聲。噪聲遵循零均值高斯分布,其標準偏差分別設置為0,0.2和0.4。結果如圖9所示,是某一傳感器節點的剩余能量百分比動態圖。黑色曲線、深灰色曲線和淺灰色曲線分別對應于σ=0,σ=0.2和σ=0.4的情況。可以觀察到,標準差較大的情況下,剩余電量的動態波動也較大,但在所有情況下,該傳感器都不會耗盡能量。這是因為基站并非工作在極限負載情況下,而是工作在最佳成本負載情況下。因此,根據本文算法的部署方案可抵抗網絡的外部變化,有很強的健壯性。 3.2.2 基站傳感器成本比 圖10展示了基站/傳感器成本比對算法給出部署結果的影響。如圖10(a)所示,隨著基站相對成本的上升,基站部署數量先逐漸下降,但當成本進一步上升后,基站部署數量的下降速度放緩。經分析可知,先逐漸下降是因為隨成本的上升,需要更多的待監測區域均攤基站成本,即單個基站的最佳負載在穩步上升;之后基站部署數量持穩,是因為基站負載能力存在上限,無法繼續通過拓展覆蓋領域的方式均攤成本。圖10(b)給出隨基站相對成本的上升,區域內傳感器數量的變化情況。可以看出,隨基站負載范圍的變大,每個待監測區域所分到時間片減少導致其充電效率降低。為應對此情況,增加了區域內傳感器節點的數量,使充電效率增加。圖10的變化趨勢證明了算法1基站最佳覆蓋范圍選擇的有效性。 本文將所提算法的性能與雙圓貪心[16](Double-Circle Greedy,DCG)算法和基于最大密度優先(Maximum Density Priority,MDP)的貪心算法進行了比較,分析不同部署策略的差異。DCG算法是一種不受現有算法限制(如需要將基站固定在一些網格點上或其他待選位置上)的基站部署算法。對于MDP算法,僅考慮將給定的待監測區域作為基站部署的待選位置,首先根據算法1計算所有待選位置的最佳覆蓋范圍;其次依據貪心思想,每輪在剩下的待選位置中挑選出可覆蓋最多待監測區域的位置,作為該輪次基站部署的位置。 3.3.1 不同參數下算法的比較 圖11展示了不同參數對各算法部署成本的影響以及不同參數下各算法的性能比較。 如圖11(a)所示,待監測數量從150增加到300,兩個算法的部署成本均逐漸變大;但本文算法中采用了均衡基站覆蓋范圍策略來平衡每個基站的工作負載,所以總部署成本優于MDP算法10%左右。對于DCG算法,由于其總是用相同大小的圓來覆蓋目標,未考慮不同的位置處,待監測區域密度也不同,表現較差。同樣地,在圖11(b)中,采樣率的增加使每個激活的傳感器節點的能耗都增加了,也需要部署更多的基站和傳感器節點,但本文算法始終優于MDP算法。而DCG算法只考慮待監測區域的位置關系,采樣率對其基站部署沒有影響,且DCG算法中基站負載能力遠未得到充分利用,采樣率的增加對其傳感器部署的影響也較小。圖11(c)中考慮了不同成本比下各算法的總成本,由于DCG算法無法根據成本比動態地調整部署策略,其部署總成本隨成本比線性增大。所提迭代算法和MDP算法都利用了基站最佳覆蓋范圍搜索算法,所以成本均小于DCG算法,其中本文所提迭代算法也總優于基于貪心的MDP算法。 3.3.2 不同算法的基站/傳感器部署成本組成情況 在其他條件相同的情況下,圖12給出了3種算法成本組成的區別。如圖12所示,本文算法中傳感器節點的數量多于貪心算法,但在基站數量上比貪心算法有優勢。這是因為貪心算法每輪次總是選擇能覆蓋最多待監測區域的位置,而忽略了基站的相對位置關系,使得最后剩余的待監測區域總是較為分散的,需要更多的基站才能覆蓋。算法2均衡了所有基站的負載,使基站負載能力得到充分利用。DCG算法未能動態地考慮不同位置上基站的負載范圍,總是用較小的圓覆蓋待監測區域,算法所需部署的基站最多。 圖12 算法部署情況比較 本文研究了定向充電中,在保證網絡可持續運行的前提下使用冗余傳感器模型降低整個網絡成本的問題。其中,基站和傳感器節點的部署相耦合,同時還要考慮基站的充電調度和待監測區域內傳感器的激活調度。本文的策略是通過求解基站的最佳覆蓋范圍,解耦基站和傳感器節點的部署,然后通過迭代算法均衡每個充電基站的工作負載,使之保持在成本最低的工作負載附近,降低了整個網絡的成本。 此外,本文通過實驗仿真來評估所提算法的性能。仿真結果證明了算法中不同步驟的有效性以及整個網絡的健壯性,并且與貪心算法相比,本文算法可以將整個網絡的成本降低約10%。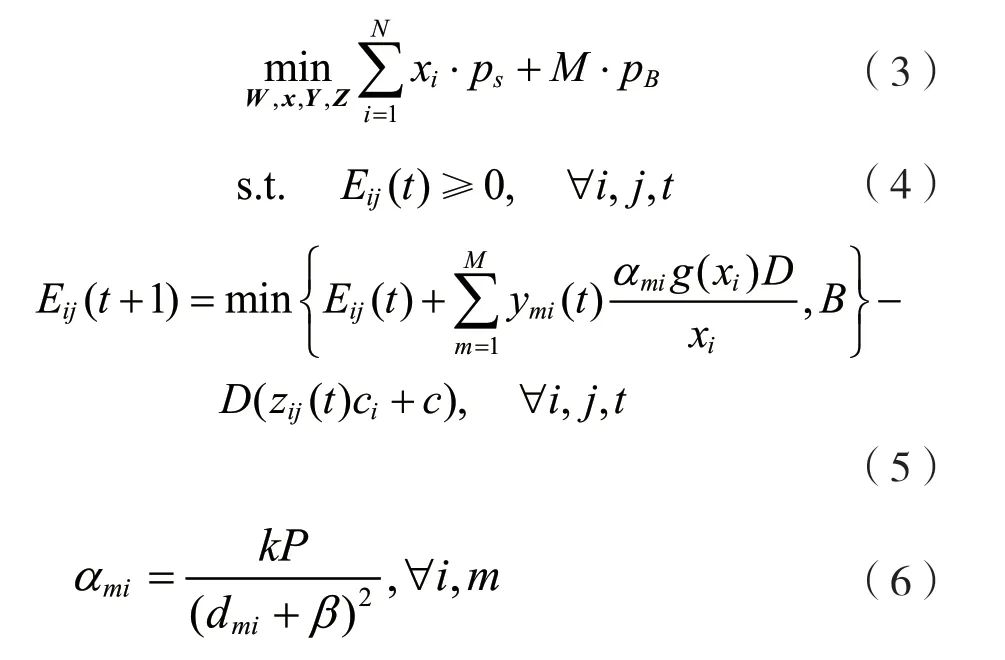
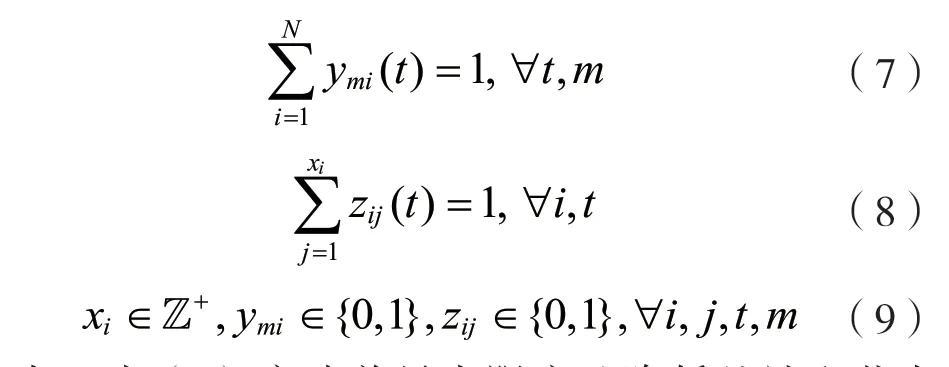
2 問題求解
2.1 添加約束
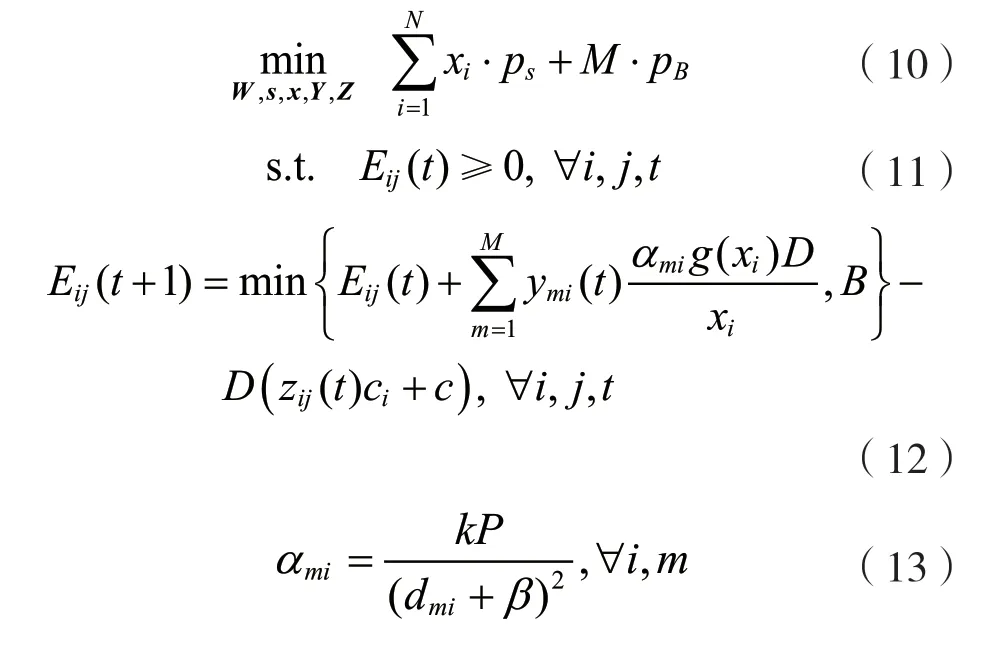
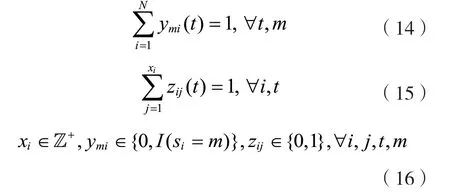
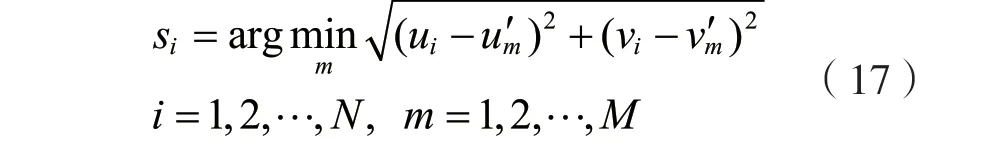
2.2 基站的最佳覆蓋范圍

2.3 基站的部署

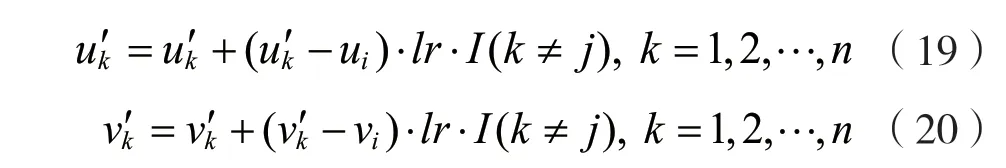
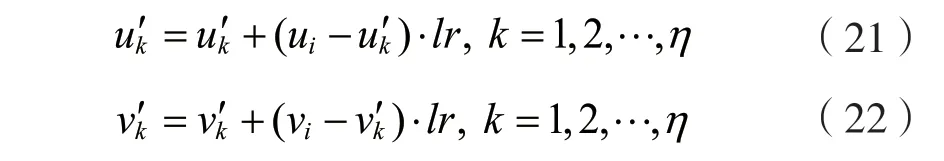

3 模擬實驗
3.1 參數設置
3.2 不同參數對本文算法的影響
3.3 算法性能對比
4 總結

