高強度合金鋼氫致斷裂有限元模擬分析

李云龍

（桂林航天工業學院 能源與建筑環境學院，廣西 桂林 541004）

在材料的冶煉過程和零件的制造與裝配過程（如電鍍、焊接）中進入鋼材內部的微量氫（10-6量級）在內部殘余的或外加的應力作用下導致材料脆化甚至開裂”被稱為氫脆。對于氫脆的機制，被認為是應力、應變和氫擴散濃度的臨界組合的結果。被廣泛接受的理論是氫降低鍵合力理論[1]（Hydrogen-Enhanced Decohes-on，HEDE）。該理論基于金屬間隙氫通過原子晶格膨脹來降低內聚強度，從而降低斷裂能的假設。基于此理論，Jiang and Carter[1]用第一原理的量子力學方法結合DFT（周期密度泛函）理論計算了不同氫濃度的bcc金屬的理想斷裂能，將該結果用于氫致金屬斷裂的模擬。Olden等[2]基于內聚力模型研究了氫影響下25%Cr雙相不銹鋼缺口拉伸平面應變試樣在海水中動態充氫條件下的氫致裂紋起裂問題。Serebrinsky等[3]提出了一種高強度鋼損傷分析的數值模式，考慮了氫的作用，模擬結果與實驗結果吻合較好，得出高強度合金鋼氫脆問題的主要機制是 HEDE。

基于以上理論和研究基礎，本研究運用ABAQUS有限元軟件建立二維CT試樣氫擴散和內聚力模型（CZM）分析耦合模型，該模型模擬了瞬態氫擴散并基于HEDE理論，通過氫在金屬中聚集引起氫附著率變化與臨界氫相關內聚力強度之間的降解耦合關系，模擬了45CrNiMoVA高強度鋼CT試樣裂紋尖端氫致裂紋萌生和斷裂，并得出結論。

1 基本理論

1.1 瞬態氫擴散分析

根據傳質理論，在非均勻介質中，由化學位梯度引起的氫擴散通量為[4]：

式中：JD為擴散通量kg/（mm2·s）；D為擴散系數（mm2/s）；R為氣體常數；x為氫擴散方向；VH為氫在金屬中的偏摩爾體積；?為正則化的氫濃度，又稱為氫在金屬中的活度，氫的濃度表示為c=?·s；s為氫在金屬中的溶解度，θ為溫度；θz為絕對零度，p為靜水應力。

1.2 與氫相關的內聚力分析

SCHEIDER等人[5]提出了梯形牽引分離定律（TSL）模型，梯形牽引分離定律具有四個參數：臨界粘聚強度σmax、彈性階段臨界分離位移δ1、塑性階段臨界分離位移δ2和最大臨界分離位移δf，具體表達式為：

式（2）中，T（δ）為牽引力與位移δ有關，δ1=0.05δf，δ2=0.65δf[10]。

由斷裂力學理論可知，內聚能Tc與材料的斷裂能GC等效：

式（3）中，KIC為材料的斷裂韌性，對于本研究的45CrNiMoVA高強度合金鋼，根據文獻[6]該材料的斷裂韌性（E為材料的彈性模量，v為材料的泊松比）。

Jiang and Carte[1]基于第一原理計算不同氫濃度對bcc金屬表面能的影響，給出了氫附著率與臨界氫相關內聚力σc（θ）max之間的耦合關系：

其中，σc（0）max是沒有氫影響的臨界內聚力。其大小一般為材料屈服應力的2～6倍[2]。在本研究中，該值是初始屈服應力的3倍。θ是為氫的附著率，與氫濃度C和氫在材料表面的吸附結合能有關，其關系表示為[7]：

其中，C表示是氫的濃度，R是氣體常數，T是絕對溫度。

2 模型建立

本研究材料采用45CrNiMoVA高強度合金鋼圓棒（直徑60 mm）。在制備試樣之前，將材料進行熱處理，熱處理工藝為：加熱（860℃，1h）后油淬，然后回火（460℃，1 h），在空氣逐漸冷卻到室溫。熱處理后對材料加工成工作段為6 mm的標準試樣進行單軸試驗，以獲得材料的力學性能，材料的力學性能為：楊氏模量210 GPa，泊松比0.3，初始屈服應力1428 MPa。在ASTME-1820標準的基礎上，將直徑為60 mm的45CrNiMoVA合金鋼圓棒制作成緊湊拉伸（CT）試樣，如圖1（a）所示。為了確保初始裂紋尖端足夠尖銳，拉伸前對試樣預制初始裂紋，預裂長度為3 mm，故試樣的初始裂紋長度為18 mm。

運用ABAQUS有限元軟件建立了二維CT模型。考慮到模型的幾何對稱性，只對試件的上半部分進行了建模，如圖1（b）所示。建模框架基于Olden[7]建立的三步分析模型：（1）模型的彈塑性應力場分析，（2）應力誘導氫擴散分析，在此步驟中氫的濃度場采用DC2D4單元，對于應力驅動氫擴散分析，假定初始氫含量均勻分布整個試樣。并假定試樣的外表面具有零氫通量邊界條件。（3）與氫相關的內聚力分析，沿裂紋擴展路徑預設零厚度粘聚COH2D4單元，來模擬模型的斷裂過程。為了使模型三步能有效的順序進行，應力場、氫濃度場和內聚力分析中的連續體采用相同的節點和單元。

圖1 CT模型示意圖

分析不同初始濃度的氫對裂紋尖端斷裂的影響，可通過對模型采用初始氫濃度0.5～2.0ppm（對應的氫活度為7.04～28.17NNC）范圍內進行模擬分析來估計氫對材料的力學性能的影響。模型的相關參數如表1所示。

表1 氫擴散參數

圖2（a）-（b）所示為彈塑性分析中靜水應力和間隙晶格位（NILS）氫濃度的分布曲線。對比圖2（a）和圖2（b）可知，裂紋尖端前沿氫濃度的分布規律與靜水應力的分布規律是一致的，最大氫濃度出現在靜水應力的最大值處。模擬結果顯示，靜水應力峰值和間隙氫濃度峰值不是位于裂紋尖端，而是略微在裂紋尖端前方。當初始氫濃度為0.5 ppm和2 ppm時，在擴散時間結束時，在裂紋尖端前方第一個單元有較高的氫濃度，分別為1.473 ppm和5.893 ppm，其值約為初始氫濃度的2.9倍（圖2（b））。該模擬結果表明，在靜水應力驅動下，間隙氫趨于集中在高靜水應力區域，該結果也體現出擴散方程的準確性。

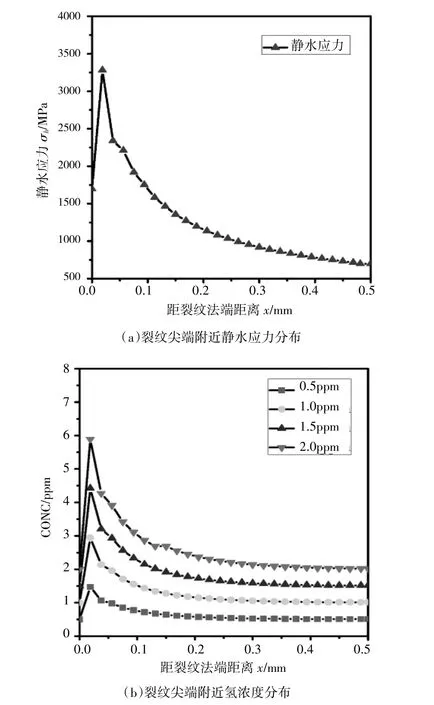
圖2 計算的靜水應力和氫濃度分布曲線

本研究的45CrNiMoVA高強度合金鋼氫致斷裂，HEDE（Hydrogen-Enhanced Decohesion）理論被認為是主導機制。由應力驅動氫擴散分析輸出的氫濃度場，該濃度場被轉移到內聚力分析中，其值在裂紋擴展過程中保持恒定，因應力誘導氫原子在裂紋尖端附近聚集，引起裂紋尖端附近氫的附著率θ增大，強度降低因子f（θ）（用于減小內聚力強度）降低（公式（4）），含氫影響的TSL降解效應就被應用到內聚力分析中。圖3（a）到圖3（b）為初始氫濃度0.5～2.0 ppm范圍變化時，氫附著率θ和強度因子f（θ）的變化曲線，可以看出，隨著初始氫濃度的增加，在裂紋尖端前方氫的附著率也隨著增大并達到最大值，與之對應的強度降低因子f（θ）在裂紋尖端前方出現最小值，氫的含量越多，裂紋尖端前沿內聚力單元的粘聚強度下降越低，從而加劇該處的內聚力單元損傷程度。最后模擬材料的氫致斷裂。

圖3 計算的氫附著率和TSL強度降低因子分布曲線

圖4（a）所示為內聚元單元法向應力隨著初始氫濃度的變化曲線，有圖4（a）中看出，當初始氫濃度等于0.5 ppm時，裂紋尖端內聚力單元開始出現損傷，但當初始氫濃度達到1.5 ppm時，裂紋尖端內聚力單元損傷程度加劇，損傷程度隨著初始氫濃度的增加而增加，當氫濃度達到2.0 ppm時，當內聚力單元法向應力降至零，裂紋尖端內聚力單元完全失效，裂紋萌生試樣開始斷裂。此時如果試樣初始氫濃度不斷增加，裂紋尖端前方將會出現大量內聚力單元損傷失效，裂紋尖端附近的內聚力單元法向應力逐漸遠離裂紋尖端，裂紋迅速擴展，直至模型完全失效斷裂。圖4（b）所示為內聚元單元最大臨界分離位移與裂紋尖端距離關系的變化曲線，水平虛線是內聚力單元的最大分離位移。對應圖4（b）的結果分析可知，當初始氫濃度低于2.0 ppm時，裂紋尖端前沿內聚力單元分離位移尚未達到臨界最大值，單元出現損傷但未失效，當初始氫濃度增加到2.0 ppm時，裂紋尖端前沿內聚力單元的分離位移超過了其最大分離位移，內聚力單元完全損傷破壞，裂紋出現萌生，模型出現斷裂。內聚力單元模擬該模型失效的準則是裂紋尖端前方第一個內聚力單元的完全分離，內聚力單元完全失效即認為裂紋萌生，因45CrNiMoVA材料是高強度合金鋼，裂紋尖端前沿一旦出現裂紋萌生，裂紋尖端不能產生鈍化，裂紋迅速發生擴展直至斷裂。

圖4 計算的內聚力單元法向應力和內聚力單元分離位移分布曲線

3 結語

運用ABAQUS有限元軟件建立二維CT試樣氫擴散和內聚力模型（CZM）分析耦合模型，開發了氫致斷裂的有限元程序，模擬了45CrNiMoVA高強度鋼CT試樣裂紋尖端氫致裂紋萌生和斷裂，得出如下結論：

（1）模擬結果顯示氫濃度的分布與靜水應力的分布是一致的。氫濃度的峰值和靜水應力的峰值都在裂紋尖端前沿的位置。該結果也驗證了氫擴散方程的準確性。

（2）氫原子在裂紋尖端高應力區域聚集，在高靜水應力區域氫的附著率達到最大值，運用HEDE氫脆機制，隨著氫附著率的增加，內聚力單元內聚能降低，內聚力強度也隨之降低，使內聚力單元在較低的應力下發生損傷破壞，裂紋在此處萌生，材料發生氫致斷裂。