基于質量集中法和迭代法的平面網衣變形模擬

楊靜宇，李 靖

（上海交通大學 船舶海洋與建筑工程學院 海洋工程國家重點實驗室，上海200240）

0 引言

隨著經濟的發展，人們的生活水平大幅提升，對水產品的需求與日俱增[1]，漁業的健康發展已成為全世界眾多國家所共同關心的問題。我國從1970年代開始發展淺水網箱，到2018年全國傳統近岸網箱數量已達到149.3萬只，2019年深水網箱的養殖體積已經達到19 358 969 m3[2]。相比于試驗，網衣的數值模擬要更加簡便和經濟[3]。近年來，隨著科技的迅速發展，計算機的計算能力也突飛猛進，有限元方法、集中質量法和質量加彈簧的模擬方法被廣泛地應用到網衣數學建模和動態模擬上。NIEDZWIED和HOPP[4]以網目為基本單位預測了網衣的形狀和載荷，并計算出中層拖網的三維形狀；PRIOUR等[5]利用有限元的方法計算出網衣下垂的形狀，并采用有限元方法研究剛度對網衣的影響；LEE等[6]將網衣離散成彈簧和質量點的結合體，模擬出拖網在運動時的狀態；TAKAGI等[7]考慮了漁網的彈性對網衣變形的影響，建立漁網的數學模型，對漁網的運動狀態進行動態模擬，在此基礎上開發出軟件NALA來計算網衣的變形；AARASNES等[8]把柔性的網衣簡化為一些平面網片鉸接在一起，將這些小網片視為由純二維平面組成，忽略了這些網片的三維特性。在國內，李玉成等[9]建立了各集中質量點的運動方程，通過Runge-Kutta-Verner方法求解運動方程，模擬結果與試驗相比吻合較好；袁軍亭[10]利用有限元理論，建立網衣的三維力學數學模型（3DNNM），計算出平面網衣和圓柱形網片的張力分布和總阻力，與試驗結果相比誤差較小；趙云鵬等[3，11]將網衣離散成質量點和彈簧的組合體，求解得到網衣在波浪中各個時刻和重力式網箱在來流中的受力和變形；孫宵峰等[12]采用隱式的Newmarkβ方法對網衣的力學模型進行求解，并建立網衣的可視化工具。

本研究將柔性網衣離散為彈簧和質量點的組合體，通過Morison公式計算網線所受水動力，并建立質量點的運動方程，基于迭代方法編程求解網衣質量點的坐標，最終得到網衣的變形和所受阻力。

1 運動方程的建立

1.1 網繩物理模型

網衣的基本單位為網繩，因此，首先建立網繩的運動方程，并將其拓展以模擬計算三維網衣。在實際應用中，組成漁網的網繩大部分都是柔性體，在水流的沖擊下形狀會發生改變，形狀的改變又會引起作用在網繩上的受力發生變化，形狀和受力之間密切相關，相互耦合。為了解決這一耦合問題，將網繩離散成無質量的圓柱形彈簧和無體積的質量點的結合體。圓柱體在水中的受力不僅與水流的相對速度也與圓柱體的方位有關，這里對該模型做出如下假設：（1）網繩只能承受拉力，不能承受壓力；（2）張力在整個橫截面上為常數；（3）網繩在拉伸過程中橫截面積保持不變；（4）兩個質量點之間的圓柱呈直線，不能發生彎曲。

完全浸沒在水中的網繩受到的重力和浮力的合力FB可以表示為：

其中，L為網線長度，dw為網線的直徑，ρnet和ρ分別指網線的密度和水的密度。

網線的直徑通常不超過1 cm，相比常見海浪的波長是小量，因此可以利用Morison公式計算網線的水動力。Morison公式為半經驗半理論公式，將靜止在水中的構件的水動力分為拖曳力和慣性力兩部分：

其中，FD為拖曳力，FI為慣性力，CD為拖曳力系數，A為沿來流方向的投影面積，CM為慣性力系數，V為來流的速度。

當構建在水中運動時，根據Brebbia和Waler[13]的建議，Morison公式可以寫為：

其中，Cm=CM-1為附加質量力系數，VR為水質點相對于構件的移動速度，R為構件的位移。

對于聚乙烯網衣，利用Wilson[14]推導的關于網繩伸長量和張力之間的關系，網繩的拉力為：

其中，T為網線所受到的拉力，L0為網繩的原始長度，L為網繩變形后的長度，彈性系數C1和C2的選取參考Gerhard Klust[15]在《纖維繩索》中彈力與變形量之間的實驗數據，對于聚乙烯材料網線彈性系數C1=345.37×106，C2=1.012 1。

對于尼龍網衣，采用H.Le Dret[16]在EZ 20 Lloyd拉力機上對直徑為4 mm的尼龍網線進行實驗并根據實驗結果擬合得到的拉力與相對伸長量之間的關系式：

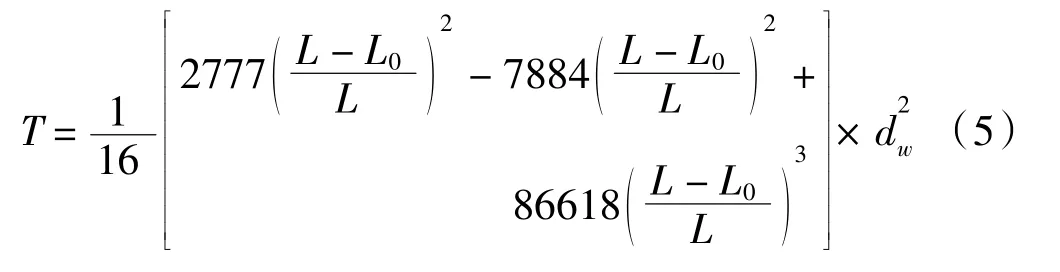
1.2 運動方程的建立

將網繩的質量和所受的重力、浮力、水動力以及拉力分配到兩端的質量集中點上，如圖1和圖2所示，在每個質量點上建立運動方程。圖2中Bi、Wi分別表示分配在第i個質量點的重力和浮力，Ti1和Ti2分別表示質量點i所受質量點i-1和i+1的拉力，Fi表示分配在第i個質量點的水動力。

圖1 網繩模型示意圖

圖2 模型質量點受力分析示意圖

根據牛頓第二定律，每一段網繩在水中的受力和加速度可以表示為：

教師要根據高職學生的實際學情，指導學生參與選擇實用性強、富有趣味的傳統文化內容，因材施教，靈活運用情境教學法、討論法、朗讀法、質疑探究法、多媒體教學法等多種教學方法，營造出傳統文化學習的氛圍，帶領高職學生走進傳統文化情境中，增進學生對有關傳統文化的理解，促進學生人文素養的提高。例如在教學《鴻門宴》這一文章時，可以用多媒體播放作者的生平介紹及課文中出現的劉邦、項羽、張良、范增等人物生平經歷、古代座次文化等知識，激發學生參與語文學習活動的興趣，讓學生更深刻地理解和掌握有關文學、文化知識，促進了高職學生人文素養的不斷提升。

其中，M為網繩的質量，將式（3）代入（6）中，可以得到：

若將離散了的每一段網繩的水動力、重力和浮力平均分配到兩端的質量點上在加上拉力，如圖2所示，得到的第i個質量點的運動方程為：

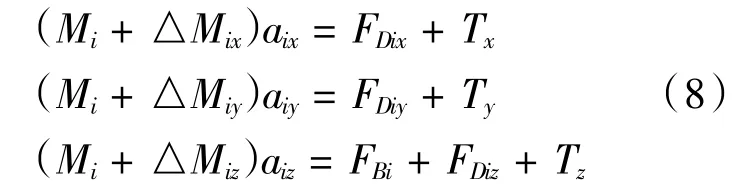
其中，Mi為分配在第i個質量點的質量，ΔMi為分配在第i個質量點的附加質量，ai為第i個質量點的加速度，下標x、y、z分別表示在大地坐標系下x、y、z三方向的分量。

2 編程計算過程

Matlab軟件是一款數學軟件，有著強大的矩陣運算功能和簡單的語法結構，使用Matlab軟件編程來模擬繩子的受力變形過程，過程如下：

（1）輸入繩子的參數：繩總長la、繩子直徑dw，分段數N，網線材料彈性系數C1，C2，網線材料密度ρnet，流速V、密度ρ、阻力系數CD和附加質量力系數Cm，計算步長δt，最終迭代進度tend。

（2）將整個繩子劃分為單獨的點，并將這些點的位置、速率、加速度進行初始化。同時，建立時間迭代步的位置、速度和加速度矩陣，并進行初始化。

（3）依照網繩質量點i當前的位置，計算出第i個點在第j次迭代中，在大地坐標系下的受力大小。

（4）由步驟（3）得到的受力大小進一步計算出節點加速度aix、aiy、aiz；根據加速度和速度計算出在該時間段內繩子的質點的運動速度Uix、Uiy、Uiz；根據加速度和速度計算出網繩質量點的位移Rix、Riy、Riz，并更新質量點i的位置。

（5）網衣的計算結果收斂時質量點受力達到平衡狀態，加速度趨于0，中間迭代過程的加速度并不影響最終的計算結果，所以兩次迭代計算的加速度的相對誤差小于0.1時，可認為當前位置已經足夠準確，進入步驟（6）進行下一節點的迭代計算，否則，令j=j+1，進入（3）繼續循環迭代。

（6）若i是最后一個點質量點則進入下一整體迭代步（t=t+δ）的計算，否則令i=i+1，j=0進入（c）中繼續進行下一節點的迭代計算。

（7）重復（3）至（6）的步驟直至計算到預先設定的迭代進度tend。

在步驟（4）中采用NewMark-β方法以增加計算的穩定性。NewMark-β方法是對物體運動的加速度做出線性變化的假定，采用該方法后速度Ui和位移Ri的基本方程分別為：

其中，Ri、Ui，ai分別表示質量點i的位移、速度和加速度。令α=0.5，β=0.25這相當于加速度在δt內為常量，其值為兩個迭代步（t，t+δt）兩端加速度的平均值。

網衣是由縱橫的網線構成，三維網衣的模型與網繩離散不同的是，質量點（i，j）周圍有4個與之相連的圓柱桿件（i，j-1），（i，j+1），（i+1，j），（i-1，j）。將每個圓柱桿件的質量平均分配到兩端的質量點上，并且質量點承擔了圓柱桿件所受的水動力、浮力、重力以及拉力，質量點所在位置即為網衣目腳交點的所在位置，如圖3所示。網衣質量點的運動方程與式（7）相同，編程求解過程與網線一致。

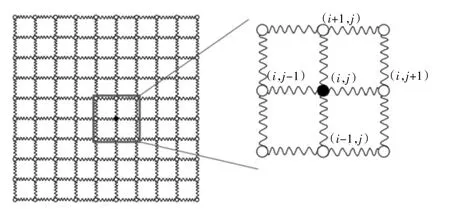
圖3 網衣離散示意圖

當流速大于0.5 m/s時，網繩軸線方向的阻力系數CDτ和垂直于軸線方向的阻力系數CDn的選取參考Casarella[17]的實驗結果，分別取0.8和1.8。沿網線軸線方向的附加質量力系數Cmτ和垂直于軸線方向的阻力系數Cmn選取，參考趙云鵬[3，18]的研究成果，分別取0.0和1.0。

3 網衣的模擬

3.1 四周固定網衣的模擬

建立單位面積（1 m×1 m）無結尼龍網衣，命名為S0，S0四邊固定，網目邊長為0.0625 m，網目數為16×16，網線直徑為0.002 m，密度為1.14 g/cm3。袁軍亭[11]在其博士論文中將網衣離散成集中質量和彈簧的組合體，建立平面網衣數學力學模型3DNNM，采用Runge-Kutta方法求解運動方程，對網衣S0模擬計算。本小節將采用迭代求解的方法，在不同的流速下，計算出網衣S0的變形和受到的水動力以及網線中的拉力，并對比兩種計算方法的結果。

設置計算的時間步長δt=10-4，t=48后結果收斂，這里的時間t并不是指物理時間，而是代表網衣質量點的迭代進度。結果如表1所示，其中，r為相對誤差，T為網線中的最大拉力，F為網片所受的總水動力，X為節點的最大偏移量，下標ite和3D分別代表本文迭代法和3DNNM方法的計算結果。

表1 不同流速下兩種計算結果的比較

網線之間的最大拉力，網衣所受的水動力以及網衣中的節點的最大偏移量隨著流速的增加不斷增大，不同流速下網衣的變形如圖4所示，網衣的最大變形量出現在中間節點。兩種計算方法相比，最大拉力之間的相對誤差在10%以內，總水動力之間的相對誤差在5%以內，最大偏移量之間的相對誤差在10%以內，當流速大于0.8 m/s后相對誤差在5%以內，表明通過迭代法求解網衣的變形的結果是可靠的。

3.2 四角固定網衣的模擬

建立模擬網衣S1，S1四角固定，方形網目大小為4 cm（網目目腳長度為4 cm），網線直徑為1.18mm，網衣邊長為80 cm×32 cm，網目數量為20×8，材料為聚乙烯。對S1進行模擬，設置流速分別為1.0 m/s、1.5 m/s和2.0 m/s。計算中迭代步長δt=2×10-5，t=50后質量點的坐標收斂，停止計算，計算結果如表2所示。結果表明，流速越大，網衣中網線的最大拉力、網衣所受的總水動力以及網衣的最大偏移量越大，不同流速下網衣的變形如圖5所示。不論是網衣S0還是網衣S1，流速越大，網衣的變形量越大，但表1和表2中Fite/V2的數值均越小。根據網衣阻力系數CDn的計算公式（11），網衣的面積An、水流的密度ρ和網線的阻力系數在模擬中保持恒定，表明影響網衣阻力系數的是形變量，且網衣的形變量越大其阻力系數越小。

圖5 不同流速下S1的變形

表2 不同流速下四角固定網衣S1計算結果

4 結語

通過將網繩離散成無質量的彈簧和質量點的模型，利用Morison公式求解網線在來流中的水動力，將網線的受力分配集中到質量點上，在質量點上建立運動方程。采用迭代方法求解各個的運動方程，并利用NewMark-β算法使迭代過程更加穩定。將網線的求解模型拓展到三維網衣，在四周固定網衣S0模擬計算中，與通過Runge-Kutta求解運動方程的3DNNM模型的結果相比，網線之間的拉力和網衣中最大的變形量的相對誤差均在10%以內，網衣的水動力的相對誤差在5%以內，表明本文通過迭代法求解網衣的變形的方法是可靠的，具有工程應用價值。在四角固定網衣S1的計算結果中發現，網衣的網繩最大拉力、總水動力和最大形變量隨著流速的提高都逐漸增大。模擬結果表明，不論是四周固定網衣S0還是四角固定網衣S1的阻力系數均隨著網衣變形量的增大而逐漸減小。