混合動力客車能量管理策略研究

胡樹良，黃 偉，陸文麗，莫錦傳

（廣西大學 機械工程學院，廣西 南寧 530004）

0 引言

能量控制策略作為油電混合動力汽車的關鍵技術，是各車企及車輛院校研究的焦點。根據實現的原理不同，可將混合動力車輛能量管理策略劃分為3類，包括基于規則、基于優化和基于智能算法的能量管理策略[1]。

基于規則型能量管理策略（rule-based energy manage system，RB-EMS）是一種實時能量管理策略，其門限規則的制定缺乏數學分析和理論基礎，導致很難準確制定。基于優化的能量管理策略分為全局優化和瞬時優化兩類。全局優化計算量大且需要知道整個循環工況，所以并不能應用于實車控制，但其仿真結果可在其他控制策略設計時作為參考[2]。全局優化依托的優化方法目前有動態規劃（dynamic programming，DP）、粒子群等，其中以DP算法最具有代表性[2-3]。瞬時優化只能求解當前的最優解，或者在滾動預測步長內的最優[4]。為逼近最優解，一般是結合多種優化算法或者采用更智能的算法[5]。如文獻[5]針對某功率分流式混合動力汽車，設計了基于粒子群優化算法（Particle swarm optimization，PSO）的具有雙層結構的多目標能量管理策略，實現了降低整車油耗和維持電池電量的目標，但是基于瞬時優化方法最終并不一定實現全局最優。

隨著AI算法和車聯網智能交通技術的發展，越來越多的學者將AI算法，如強化學習，應用到混合動力汽車的能量管理策略的設計，提出適應性更強，控制效果更好的智能能量管理策略[6-10]。研究表明，強化學習算法在混合動力能量管理策略方面的應用具有很好的適用性，經過學習訓練可快速自主收斂到全局最優解。文獻[9]針對一款插電式混合動力汽車設計了由強化學習框架訓練和生成的智能SOC（State of charge）分配策略，研究表明油耗明顯低于兩種常用的SOC分配策略。自適應動態規劃（adapted dynamic programming，ADP）具有DP算法和強化學習兩種算法的優勢，能在避免“維數災”的同時使系統自主收斂到一個最優的全局近似解，在無人機控制、航天器控制等研究方向具有廣泛的應用[11-12]，并取得不錯的控制效果。

以國內某雙行星排混合動力客車為研究對象，以提高整車燃油經濟性和維持SOC平衡為目標，基于Matlab仿真軟件，對混合動力客車（HEV）進行整車建模，然后搭建基于ADHDP算法能量控制策略，并在C-WTVC工況下與自適應等效燃油消耗最小控制策略（adapted equivalent consumption minimization strategy，A-ECMS）、基于DP算法控制策略進行仿真對比分析。

1 雙行星排混合動力客車建模

1.1 整車結構及參數

基于Matlab仿真軟件，對國內某雙行星排混合動力客車（HEV）進行整車建模，整車參數見表1。

給定客車車速ua，需求功率Pdem可由下式計算得出：

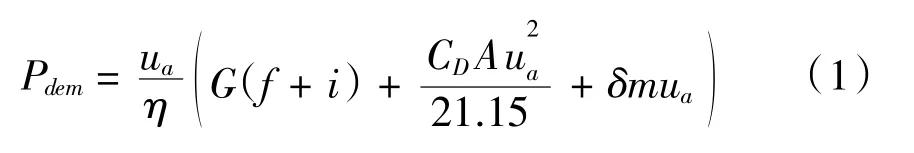
其中，f、i為滾阻系數和道路坡度；CD和A為風阻系數和迎風面積，δ和m為旋轉質量系數和整備質量。

1.2 雙行星排動力耦合機構分析

整車結構如圖1所示，公交車傳動系統采用雙行星排動力耦合結構，發動機、電機MG1分別與前行星排P1的行星架、太陽輪相連，通過控制b1、b2離合器的開關可實現多種工作模式。電機MG2與后行星排P2的太陽輪相連，后行星排齒圈固定，前行星排P1的齒圈與后行星排P2的行星架相連，經主減速器傳遞動力至車輪以驅動車輛。

圖1 雙行星排式混合動力公交車整車結構

不計行星齒輪耦合機構的內部摩擦和轉動慣量，根據發動機、電機MG1、電機MG2與前后行星排的連接方式，可推算出輸出轉速轉矩的關系：

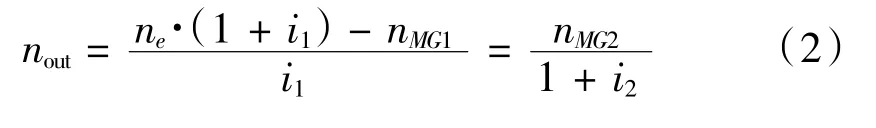
式中，uout、Tout分別為雙行星排輸出軸的轉速和轉矩；ne、nMG、nMG2分別為發動機、電機MG1和電機MG2的轉速；Te、TMG2分別為發動機、電機MG2的轉矩。行星排參數見表1。

1.3 發動機、電機、電池模型

發動機的參數見表1，基于發動機臺架數據，通過數值建模得到發動機準靜態模型，如圖2所示。

圖2 發動機燃油消耗率map圖

電機參數（表1），MG1和MG2模型也通過數值模型建立，如圖3所示。

圖3 電機2效率map圖

電機轉矩為正時處于驅動狀態，電機轉矩為負時處于發電狀態。驅動和發電的電機功率計算分別為：

式中，nm、Tm為電機的轉速和轉矩，η為電機效率，Pm_dis為電機處于驅動狀態時的功率，Pm_chg為電機放電時提供的功率。

電池模型選用電池內阻模型，電池功率計算式為：

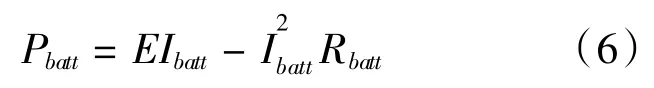
式中，Pbatt為電池功率；E為電池開路電壓；Ibatt為電池電流；Rbatt為電池總內阻。E與電池的荷電狀態SOC有關，如圖4所示。

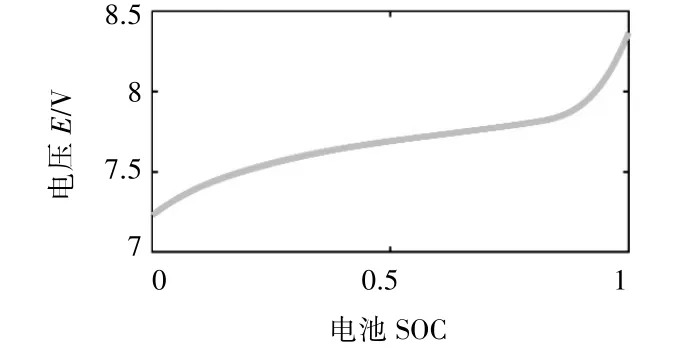
圖4 電池模型

由此求得電池電流

則電池SOC可由下式計算：

式中，SOC（t）為電池經過充放電時間t后的S OC；SOC0為電池的起始S OC；CAh為電池容量。

2 控制策略的設計

2.1 動態規劃

DP算法是由美國數學家R.E.Bellman等人基于最優性原理提出。應用解決多階段決策問題的一般步驟為：首先需要對所研究的多階段決策問題進行階段的劃分；其次需要確定優化過程中的狀態變量、控制變量與狀態轉移方程；最后須確定單個階段成本函數和全過程的最優目標函數，從而建立動態規劃基本方程。

式中，x為狀態變量，u為控制變量，L（x0，u0）為單步成本函數，J[x]為系統的總代價函數。

將電池SOC作為優化過程中的狀態變量，發動機轉速作為控制變量，設計單步成本函數：

fue l（xk，uk）為第k步等效油耗，SOC（k）為電池荷電狀態，λ為油電轉換系數，則通過遞歸求解，可獲得全局最優的控制變量和電池SOC的最優軌跡。

2.2 基于自適應動態規劃算法能量控制策略

2.2.1 基于自適應動態規劃算法能量控制策略結構

自適應動態規劃（ADP）源于向前動態規劃，最早由Werbos首先提出[12]，其將執行網（Action）和評價網（Critic）組成一個智能體，Action作用于系統后，基于貝爾曼原理，通過環境在不同階段產生獎勵/懲罰來更新Critic的參數。自適應動態規劃具有DP算法和強化學習兩種算法的優勢，能在避免“維數災”的同時使系統自主收斂到一個最優的全局近似解。強化學習所研究的是智能體和環境的序貫決策過程，在數學上其規范為一個馬爾科夫決策過程（Markov Decision Process，MDP）。一個馬爾科夫過程由一個五元組（S，A，P{s|a}，γ，R）構成，S表示狀態集，A表示一組動作，P{s|a}表示狀態轉移概率，γ表示折扣因子，R為回報函數。

定義狀態集S的三個分量為電池SOC、需求車速ua和需求功率Pdem，并將這三個分量作為執行網的輸入，如圖所示。定義發動機的轉速ne作為系統采取的動作，即為執行網的輸出。回報函數R為L（k）函數的期望，如下：

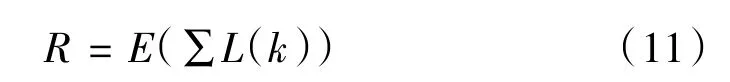
將系統狀態集和執行網的輸出作為評價網的輸入，其輸出為系統總代價函數的估計J＾，采取TD方法對評價網網絡權值進行更新，TD的誤差可通過擬合動態規劃基本方程獲得，該方程為：

式中，EC為TD誤差，J＾（k）為評價網的輸出，即總代價函數的估計值，L（k）為單步成本函數。

根據最優性原理，最優控制應滿足一階微分必要條件，故執行網可通過策略梯度實現網絡權值更新。如圖5所示。

圖5 ADP算法能量控制策略結構

2.2.2 ADP求解過程

基于在“策略改進程序”和“值確定運算”之間循環，ADP算法的求解原理如下：

（1）策略改進程序

策略改進在“執行網”進行，給定一個控制律ui，可計算系統下一個狀態轉移xk+1和對應的代價Ji（xk+1，ui），則依據下式改進控制律：

式中，ui+1為改進的控制律；L（xk，ui）為系統的效用函數；J（xk+1，ui）為系統在控制律ui作用下從狀態xk轉移至xk+1的累計成本。

（2）值確定運算

值運算在“評價網”進行，給定一個控制律ui，則代價函數可依據下式更新：

當循環產生兩個相同的控制律或著連續的兩個控制律相差在一定精度范圍內，算法終止。

求解過程應在發動機、電機允許工作的轉速、轉矩范圍之內進行計算：

式中，ne、Te為發動機的轉速和轉矩；nm、Tm為MG2的轉速和轉矩；ng、Tg為MG1的轉速和轉矩。

為了避免出現電池過充過放等不利于電池長期使用的現象和提高電池的充放電效率，需要限制電池始終保持工作在最大充電功率與最大放電功率區間內，同時限定電池的SOC工作區間。

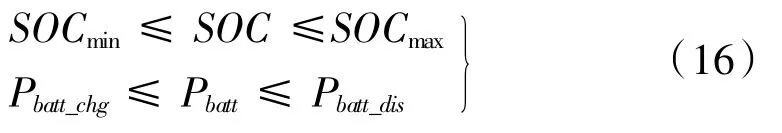
式中，SOC為電池荷電狀態；Pbatt為電池功率。

3 仿真分析

在Matlab軟件平臺下基于C-WTVC工況，對ADP控制策略進行仿真；并將仿真結果與自適應等效燃油消耗最小控制策略（A-ECMS）、DP控制策略的仿真結果進行對比分析。

從圖6中可以看出，值確定誤差經過1000次訓練后，評價網誤差穩定在設計2×10-3范圍，表明ADP控制策略具有良好的適應性。

圖6 評價網誤差均值

由圖7～11可以看出，三種控制策略在低速工況均傾向于選擇純電動模式，在市區和公路循環的工作模式差別不大；而在高速循環工況下，ADP與DP的選擇模式更接近，即更傾向于混動模式，有利于維持SOC的穩定。同時在ADP控制策略下的發動機工作點與DP的也更接近。

圖7 DP電機MG2工作點

圖8 ADP電機MG2工作點

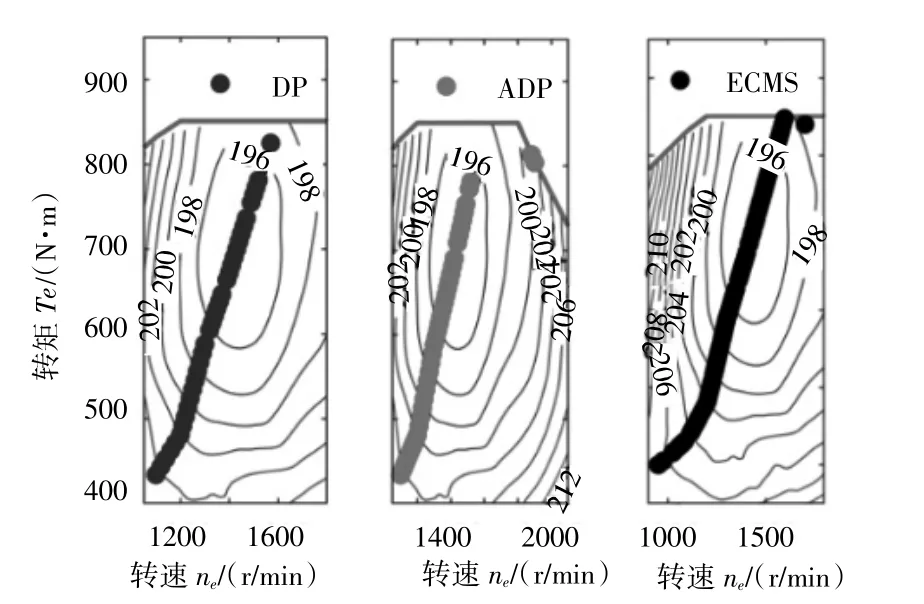
圖9 發動機工作點

圖10 混動模式占比

圖11 仿真電池SOC軌跡

通過分別統計混動模式和純電動模式在驅動模式的占比可以看出，三種控制策略的混動模式占比均達到47%以上，差距不大（表2）。從原理上分析，深度混動的驅動能量的來源最終是來源于發動機，合理減少純電動驅動次數，在維持電機對發動機的工作點的調節所需的能量的前提下，可減少能量轉換，從而減少能量損失，提升整車燃油經濟性。

表2 驅動模式

從表3仿真結果可以看出，ADP和DP在維持SOC平衡方面要優于A-ECMS，雖然電池SOC值均能回到初始值60%附近，但是仿真過程A-ECMS的SOC波動更大。在油耗方面，盡管DP具有優異的表現，百公里油耗僅為15.89 L，但是仿真時長達到了1 h15 min，并不合適于實車控制；而ADP在仿真時間僅需25 s的同時百公里油耗僅為18.12 L，較DP算法控制策略的差距僅為10.77%，展現了其可應用于實車控制的良好前景。

表3 仿真結果

4 結語

（1）經過訓練，ADP能量管理策略可快速到全局最優解，展現了ADP算法具有良好的適應性。

（2）三種控制策略在低速工況均傾向于選擇純電動模式，而在高速循環工況下，ADP與DP的選擇模式比較接近，即更傾向于混動模式。

（3）ADP控制策略達到了維持SOC平衡的目標的同時，百公里油耗與DP算法控制策略的差距僅為10.77%，具有較好的燃油經濟性，擁有可應用于實車控制的良好前景。