一種新型電容式六維力/力矩傳感器設計及解耦分析
姚起宏,王奉陽,黃 偉,2,蒲明輝,2
(1.廣西大學機械工程學院,廣西 南寧 530004;2.廣西大學 廣西制造系統(tǒng)與先進制造技術重點實驗室,廣西 南寧 530004)
0 引言
六維力/力矩傳感器能夠?qū)崿F(xiàn)空間直角坐標系中3個方向力分量FX、FY、FZ和3個方向的力矩分量MX、MY、MZ的測量,其作為實現(xiàn)工業(yè)智能化重要的設備之一,廣泛應用在機械加工、汽車制造、智能化機器人、航空航天等領域[1,2]。力傳感器種類較多,目前國內(nèi)外已經(jīng)有較成熟的六維力/力矩傳感器。按力信號轉換方式可分為應變式、壓電式、壓磁式、光學式電容式等[3,4],其中應變式力傳感器是目前研究最多、應用最為廣泛的一種力傳感器[5-6]。應變式力傳感器靈敏度高、響應快,但其結構和電路設計都很復雜,力矩解耦困難。在測量時需要額外的A/D轉化器,才能完成。其應變片對粘貼精度要求高且容易損壞,對電磁噪聲過于靈敏[7];電容式力傳感器具有結構簡單、靈敏度高、動態(tài)性能好、能實現(xiàn)非接觸式檢測等優(yōu)點。同時,目前國內(nèi)電容式六維力/力矩傳感器的研究相對較少,故對電容式傳感器進行深入研究有一定的實際意義。
傳統(tǒng)的電容傳感器可分為3類:極距變化型、面積變化型和介質(zhì)變化型[8]。但由于邊緣效應的存在,會出現(xiàn)非線性誤差。隨著電容邊緣效應的研究不斷深入,基于電容邊緣效應原理的傳感器的實現(xiàn)將成為可能。
本研究基于平行極板變極距電容原理和電容邊緣效應原理,采用一種新型的雙十字差動式結構,通過極板對于不同分量的力的差動關系,對六維力/力矩傳感器的測量進行解耦。并通過仿真實驗驗證了該傳感器的解耦特性,為后續(xù)的物理實驗奠定了一定的基礎。
1 電容式六維力/力矩傳感器原理分析
1.1 平行板變極距式電容傳感器
當忽略電容邊緣效應時,平行極板間電容量C的計算式為:

式中ε=ε0·εr為介電常數(shù);ε0為真空介電常數(shù);εr為極板間介質(zhì)的相對介電常數(shù);S為兩極板的相對有效面積;d為兩極板間距。
變極距平板電容傳感器的結構原理圖如1。
圖中,上極板為靜電極,下極板為動電極,d0為兩極板初始間距,當動電極移動了△d,電容量變換了△C,初始電容為C0。電容相對變化量為:

當△d/d0<<1時,由泰勒公式得其理想擬合方程:

其理論線性度δL:

式中△m為最大擬合偏差,Y(FS)為傳感器的滿量程輸出。
由式(2)~(4)可知,變極距型平板電容傳感器△C與△d理論上為非線性關系,當極距變化很小時可近似為線性關系,故其常用于小位移變化的測量中[9]。
由式(3)可得變極距型平板電容傳感器的靈敏度Kd為:

由式(5)可知變極距平行極板電容傳感器的靈敏度和極板面積正相關,和極板間距成負相關。
1.2 垂直板變極距式電容傳感器
動極板和靜極板采用垂直布置的形式,如圖2所示,靜極板非常薄,僅0.1μm,兩極板間距h,靜極板寬度為W,高度為H。當在兩極板間施加電壓時,兩極板將形成一個邊緣場[10,11]。兩極板產(chǎn)生的邊緣電容為[12]:


圖2 電容邊緣效應垂直式結構
當極板間距變化△h時,初始電容C0改變△C:
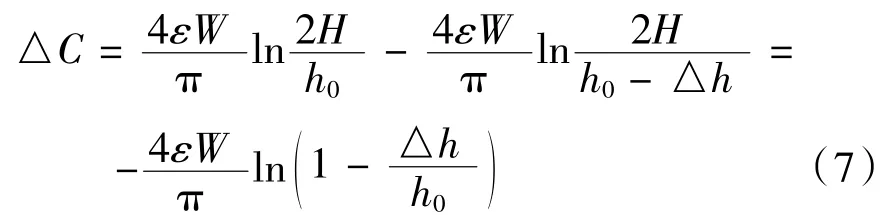
將式(7)進行泰勒展開得:
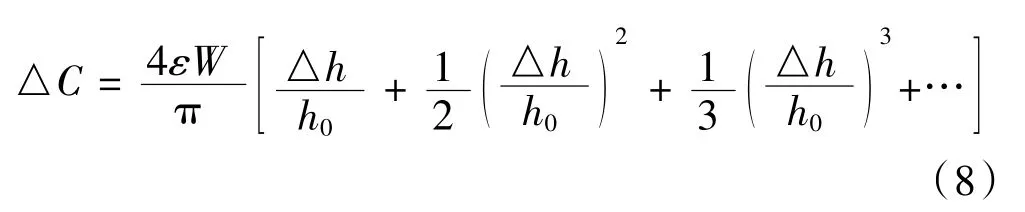
當動極板位移量遠小于極板初始間距時,即△h遠小于h0時,忽略式(8)中高階項,得:

則最大擬合偏差Δmax:
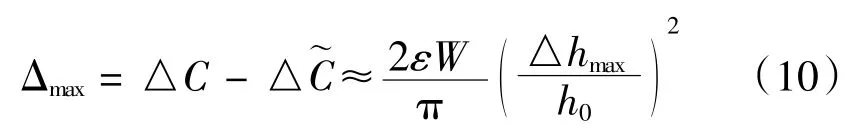
將最大變形量Δhmax和最小變形量0代入式(9)可得基于垂直極板的電容式力傳感器滿量程輸出Y(FS)為:

理論線性度為:
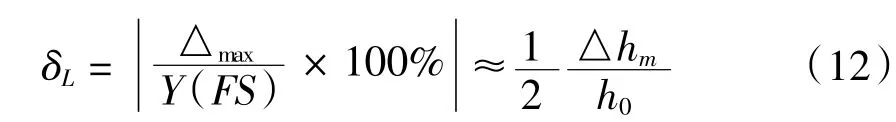
對比式(4)和(12)可得,基于電容邊緣效應的變極距垂直型電容傳感器的輸入輸出特性為非線性,但其線性度相對平行板線性度提高了一倍。
根據(jù)式(9)可得靈敏度Kvert:

式中h0為兩極板初始間隙。
根據(jù)式(13)可知,變極距垂直型電容傳感器的靈敏度Kvert與靜極板的寬度W正相關,與兩極板初始間隙h0負相關,與靜極板高度H無關。
若設平行極板的面積S=W H,極板間距d0=h0,則由式(5)可得變極距平行板電容傳感器的靈敏度為:
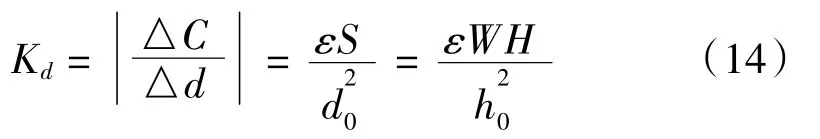
比較(13)和(14)兩式可知,電容邊緣效應變極距垂直型電容傳感器的靈敏度Kvert相比Kd在僅考慮極板間距的情況下受到極板間距的影響更小,即其靈敏度更穩(wěn)定。
2 傳感器結構設計
該傳感器主要應用于協(xié)作機器人末端關節(jié)力的測量,根據(jù)應用場景,傳感器的量程見表1。

表1 傳感器量程
傳感器結構圖如圖3,整體結構如圖3所設計傳感器結構圖如圖3,整體結構如圖3(a),下層S型彈性梁起到X、Y方向分力的解耦作用,并能提高傳感器的靈敏度,考慮到加工可行性,將本傳感器進行分層,如圖3(b)。傳感器工作時,外圈固定,內(nèi)圈受力帶動測量層產(chǎn)生位移,通過PCB電路板檢測由此引起的電容量的變化。

圖3 傳感器結構圖
3 測量及解耦分析
傳感器的信號傳遞過程見圖4,前而已對位移和電容之間關系進行了詳細分析,這里測量及解耦驗證時僅考慮力-位移之間的關系。

圖4 信號傳遞圖
測量結構平面見圖5,采取雙十字結構布置電容器極板。圖5中的虛線為電容器靜電極,靜電極布置在PCB板(在圖7中未顯示)的下底面上,其厚度方向(垂直X Y平面方向)的尺寸很小,在5μm~105μm范圍,這是由PCB板覆銅工藝所決定的。其中C1~C4為垂直極板布置方式,原理示意圖見圖2,C5~C8為平行極板布置方式,原理示意圖如圖1,采取了上文描述的兩種電容測量原理實現(xiàn)六維空間力/力矩的測量。

圖1 變極距型電容傳感器原理圖
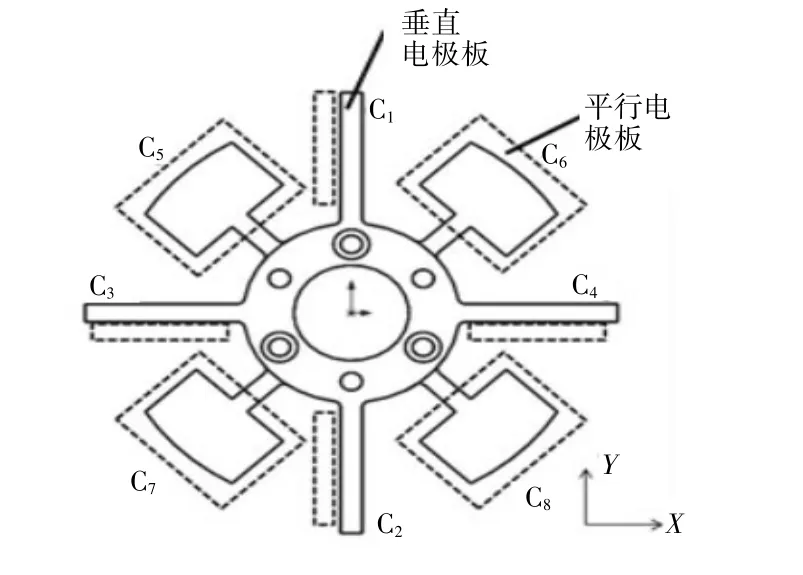
圖5 測量體平面結構
各維力測量原理 切向力FX通過垂直電極板測量(FY同理),如圖6(b)所示,受到X方向力后,垂直布置的電極板極距發(fā)生變化,從而引起電容量變化,通過檢測電容量的變化達到測量目的。Z方向的力矩M Z通過C1和C2,C3和C4之間的差動關系進行測量,如圖6(c)。
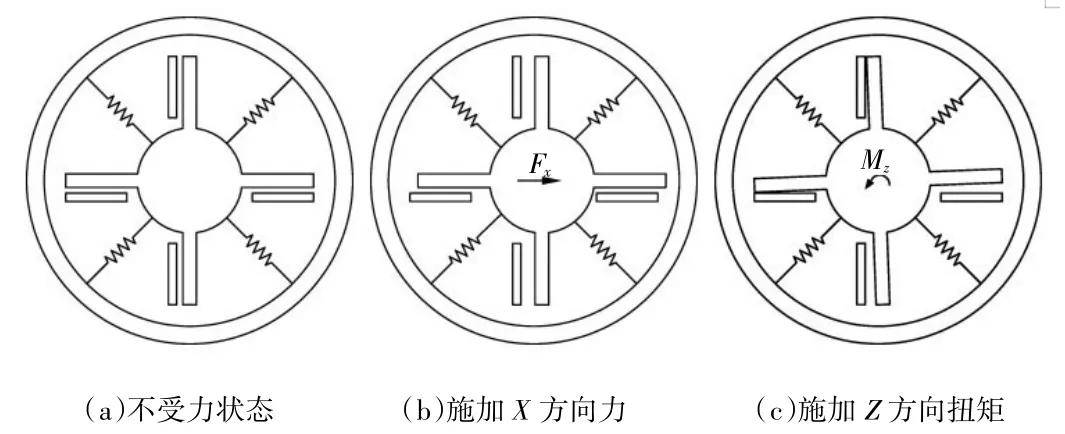
圖6 Fx、Fy和Mz的測量原理
法向力FZ和力矩MX、MY移引起電容的變化見圖7。FZ作用時,所有平行極板電容器極矩變小電容增大(圖7(b))。當受到MX時(MY同理),如圖7(c),兩側平行布置的極板,一側間距增大,另一側減小,通過這種差動式關系來進行MX的測量。

圖7 法向力和力矩的測量原理
表2列出了每個電容器受到各正向力/力矩時電容變化的趨勢。在表中,“?”和“?”代表相對強勁的電容的增加和減少,“↑”、“↓”分別表示相對較弱的增加和減少。“~”意味著電容幾乎沒有改變。

表2 電容隨相應力的變化趨勢
由表2可知,每個電容器在6種不同的力分量輸入下變化趨勢不同。此處分析僅考慮位移和力的關系,假設輸入力與位移變化呈線性關系,可以建立此傳感器的位移和力之間的測量方程為:

其 中F= [Fx,F(xiàn)y,F(xiàn)z,Mx,My,Mz]T,△h=[△h1,△h2,△h3,△h4,△h5,△h6,△h7,△h8]T,T為6×8的標定矩陣。
4 解耦可行性的仿真驗證
對傳感器結構建立有限元模型如圖8。

圖8 傳感器機械結構有限元模型
對外圈施加固定約束,內(nèi)圈通過rbe3單元進行加載。由于有限元分析材料為彈性材料,在應力小于材料屈服強度時位移和力的關系是線性的,仿真分析時僅對力各分量滿量程單次加載,對C1~C8電容所產(chǎn)生的有效測量位移進行提取(均取動極板節(jié)點位移的平均值),并根據(jù)式(15)計算標定矩陣T。
進一步任取3組力進行仿真,提取測量位移數(shù)據(jù),對解耦矩陣進行驗證,數(shù)據(jù)表見表3。

表3 解耦誤差分析
通過式(15)計算所得的力和實際施加的力進行對比發(fā)現(xiàn),仿真解耦計算結果和實際施加力之間誤差不超過0.9%,可見誤差較小解耦效果較好,故仿真驗證初步滿足解耦要求。
5 結束語
(1)本研究設計的六維力/力矩傳感器的測量原理,采用基于電容邊緣效應和平行板變極距電容原理進行測量,理論分析表明其整體線性度比僅采用平行板電容傳感器要好,同時垂直和平行兩種極板的結構布置方案能更好地利用空間,使所設計的傳感器結構更加緊湊。
(2)測量體采用雙十字式結構,通過不同極板之間的差動關系進行解耦,測量原理簡單;并通過仿真驗證了解耦的可行性,為后續(xù)靜態(tài)物理標定試驗打下了一定的基礎。

