極寒大溫差環境下溫度對軸承配合的影響及自適應補償結構
唐術鋒,王旭,張慧杰,姚佳男,程曦
(1.內蒙古工業大學 機械工程學院,呼和浩特 010051;2.內蒙古自治區特殊服役智能機器人重點實驗室,呼和浩特 010051)
在極地、高原科考以及深空探測等極寒大溫差環境下,轉動關節零件會發生變形,材料不同,變形不同,從而影響零件配合精度,甚至造成設備不能正常運轉[1]。
國內外關于溫度對機械零件配合精度的研究很多:文獻 [2-3]分析了熱誤差對機械零件配合精度的影響,提出了機械熱變形的補償方法,分析了減少熱誤差的措施;文獻[4]通過徑向熱變形試驗分析了材料雙層管間隙熱變形量的影響因素,得出材料雙層管間隙的熱變形量與材料種類和雙層管內外徑尺寸有關;文獻[5]根據機械零件熱變形和熱膨脹規律提出了熱誤差補償技術理論,通過該理論可減小零件配合精度的變化。
上述研究采用溫控技術、材料優化、熱誤差補償等方法減小了溫度對機械零件配合精度的影響,但大多需要復雜的系統。在此提出一種極寒大溫差環境下消除熱應力及熱變形影響的自適應溫差結構。
1 極寒大溫差環境下軸承配合處應力及變形
以某極寒大溫差環境(溫度從22 ℃下降到-60 ℃)下旋轉關節處緊配合的外殼與圓錐滾子軸承外圈(圖1)為例分析,在極寒環境下將其視為剛性連接。外殼材料為硬鋁合金,軸承外圈材料為GCr15,其主要結構參數見表1,材料參數見表2。為方便計算,根據幾何特點將外殼和軸承外圈簡化為厚壁圓筒[6]。
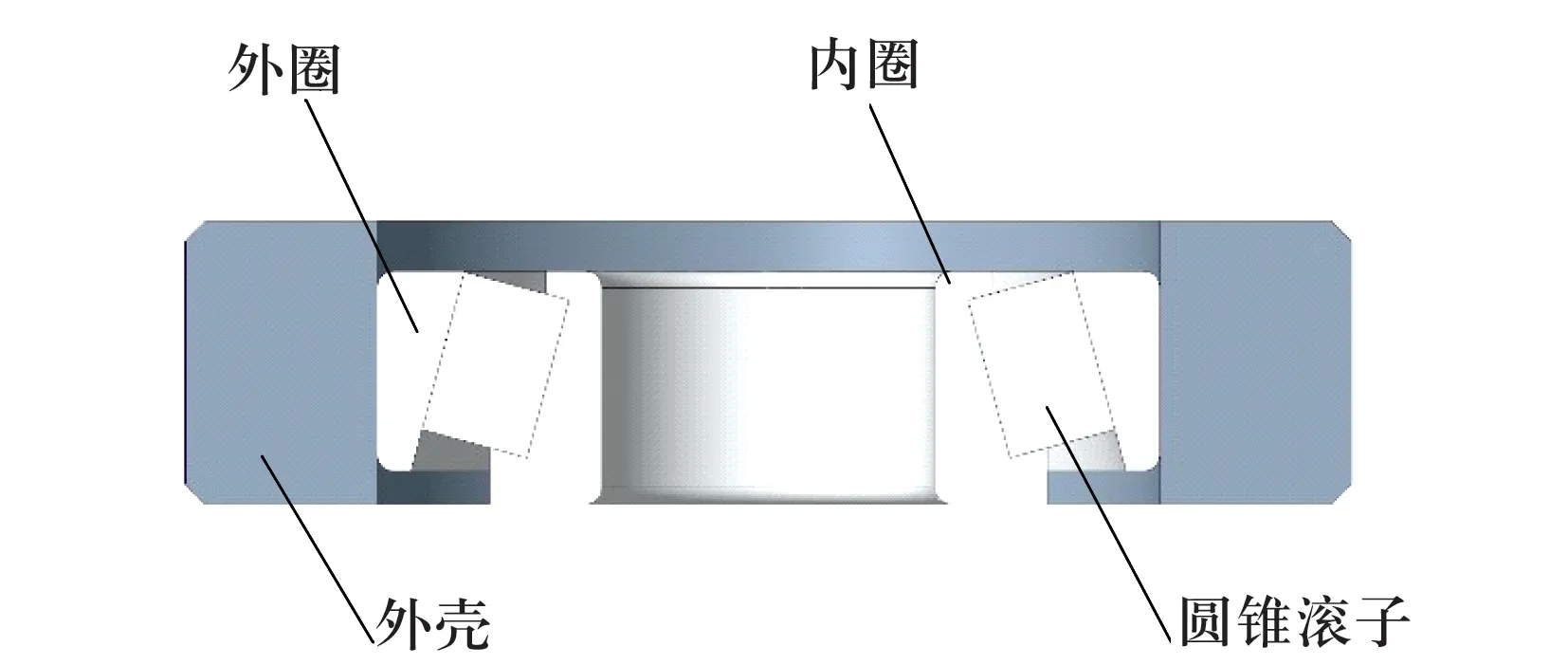
圖1 外殼與軸承外圈配合示意圖

表1 外殼與軸承外圈主要結構參數
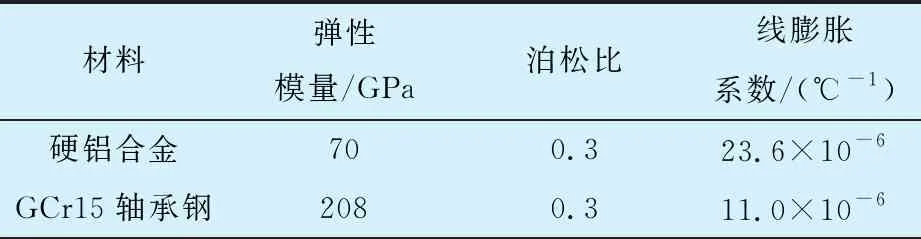
表2 外殼與軸承外圈材料參數
1.1 理論分析
同一變化的溫度場中,2個緊配合的零件由于熱膨脹系數不同,變形不同,無法自由脹縮,從而產生不同的熱應力。
基于彈性力學和傳熱學理論可得外殼A與軸承外圈B的熱變形uA,uB,可表示為
(1)
式中:αA,αB分別為外殼、軸承外圈的線膨脹系數;rAI,rAO分別為外殼的內、外半徑;rBI,rBO分別為軸承外圈的內、外半徑;TA(r),TB(r)分別為外殼、軸承外圈沿半徑方向的溫度[7]。
同一溫度場中外殼與軸承外圈溫度變化相同,則(1)式也可表示為
(2)
式中:ΔT為溫度變化量。
外殼與軸承外圈在極寒大溫差環境下的變形如圖2所示。在初始溫度為22 ℃時,軸承外圈內外表面分別在a,b點所在弧面,外殼內外表面分別在b,c點所在弧面,配合面為b點所在弧面。當外界溫度下降到-60 ℃時,外殼與軸承外圈自由收縮。若兩者之間無相互約束,由(2)式可得uA=0.045 477 mm,uB=0.021 195 mm。外殼內表面由b縮小至m所在弧面,軸承外圈外表面由b縮小至n點所在弧面。由于2個零件在配合面固定,徑向與周向不能相對移動,約束作用使外殼實際收縮量小于自由收縮值,外圈實際收縮量大于自由收縮值。

圖2 外殼與軸承外圈的熱變形示意圖
熱脹冷縮作用下相互約束的零件在徑向平面上會同時受徑向與周向彈性應力的作用。因周向尺寸遠大于徑向尺寸,外殼與外圈在約束下收縮產生的熱應力主要集中在周向。熱應力使外殼周向方向伸長,軸承外圈周向方向縮短,如圖3所示。
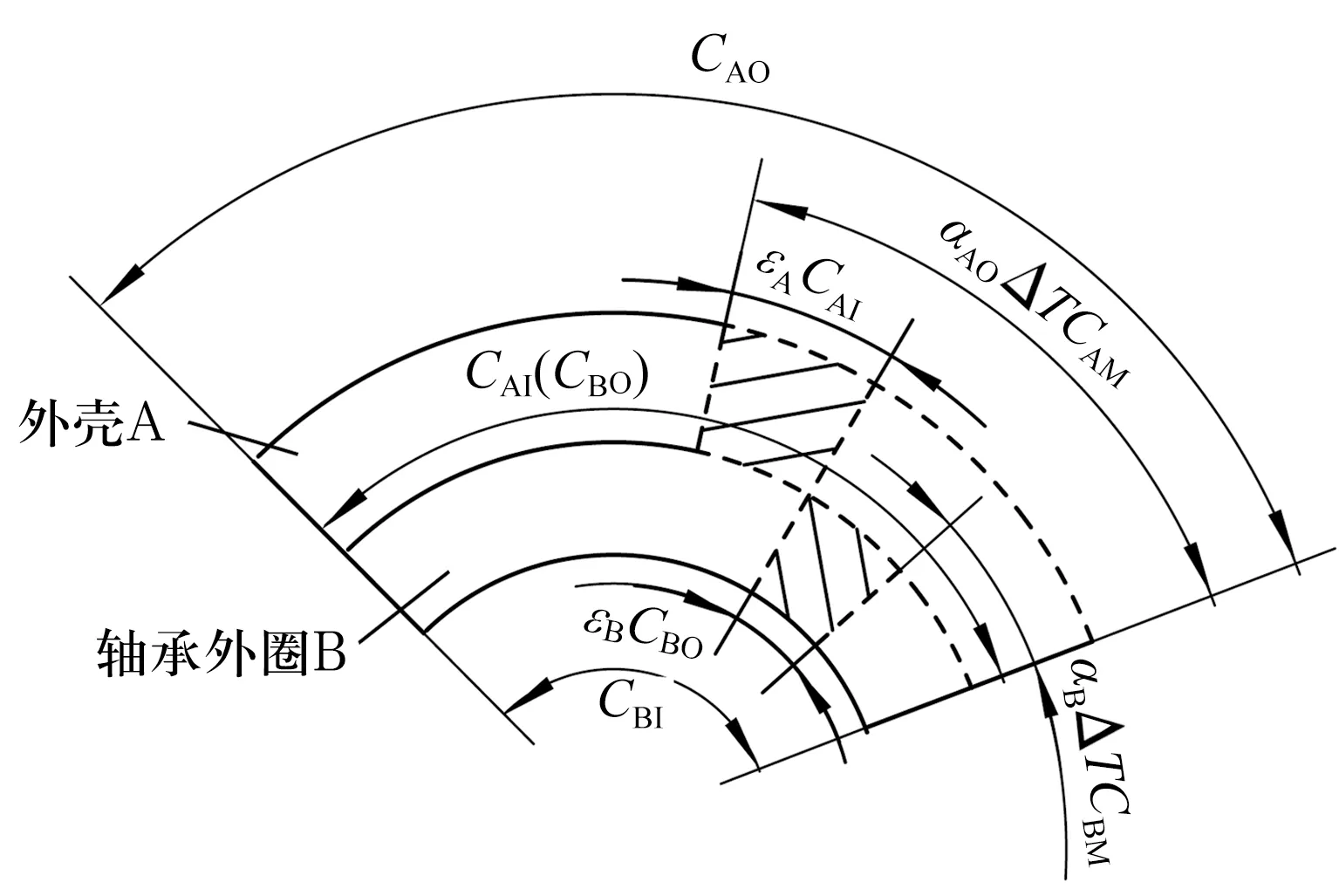
圖3 外殼與軸承外圈周向尺寸變化示意圖
在溫度降低時,外殼在接觸面處受周向彈性拉應力σA作用,從m點移至p1點所在弧面,軸承外圈受周向彈性壓應力σB作用,從n點移至p2點所在弧面。p1,p2點所在弧面在應力作用下最終接觸,即新的熱穩態下外殼與軸承外圈配合面。
由胡克定律可知外殼的周向彈性應變為
εA=σA/EA,
(3)
外殼中徑位置的周向伸長量為
εACAM=σACAM/EA,
(4)
CAM=(CAI+CAO)/2,
式中:EA為外殼彈性模量;CAM為外殼中徑面圓弧周長;CAI,CAO分別為外殼內、外徑面圓弧周長。
軸承外圈周向應變為
εB=σB/EB,
(5)
軸承外圈中徑位置的周向伸長量為
εBCBM=σBCBM/EB,
(6)
CBM=(CBI+CBO)/2,
式中:EB為軸承外圈材料彈性模量;CBM為軸承外圈中徑面圓弧周長;CBI,CBO分別為軸承外圈內、外徑面圓弧周長。
外殼與軸承外圈周向尺寸沿徑向由內至外線性增大,最終周向收縮量與周向長度正相關,采用中徑處尺寸代替整體尺寸平均值。外殼周向收縮量為
αAΔTCAI-εACAM=αAΔTCAI-δACAM/EA,
(7)
軸承外圈周向收縮量為
αBΔTCBO-εBCBM=αBΔTCBO-δBCBM/EB,
(8)
式中:δA,δB分別為外殼、軸承外圈軸向長度。
由于外殼與軸承外圈剛性連接且保持原有形狀,周向尺寸實際變化相同,即
Δlt=αAΔTCAI-δACAM/EA=
αBΔTCBI-δBCBM/EB。
(9)
當處于平衡狀態時,配合面保持剛性接觸,在周向剖面上外殼所受拉力與軸承外圈所受壓力相等,即
σASA=-σBSB,
(10)
SA=(rAO-rAI)δA,
SB=(rBO-rBI)δB,
式中:SA,SB分別為外殼、軸承外圈截面面積。
由(9),(10)式可得
(11)
(12)
周向收縮量與徑向收縮量的關系為
CAI+Δlt=2π(rAI+Δlr),
(13)
式中:Δlr為外殼和軸承外圈由于約束作用在接觸面的徑向位移。
由于溫度變化,軸承外圈自身也會沿徑向收縮,軸承外圈在極寒大溫差環境下的徑向位移為
ΔlBI=Δlr-(rBO-rBI)αBΔT。
(14)
外殼和軸承外圈的應變為
(15)
1.2 有限元分析
1.2.1 建模
根據表1和表2的數據建模并導入ANSYS Workbench,采用掃掠法進行網格劃分,由于熱應力產生的彈性應變相對整體尺寸較小,在此選用0.8 mm的網格。劃分后有限元節點數為608 943,單元數為140 625。
1.2.2 變溫過程模擬
施加溫度場:初始溫度設置為22 ℃,共設置4個載荷步,載荷步長為1 s,第1步溫度下降22 ℃,其余載荷步溫度降低20 ℃。
外殼與軸承外圈的接觸面會向3個方向產生變形,在降溫過程中2個零件周向與徑向始終保持接觸,在過盈配合下軸向會受到限制而不能自由變化,若用綁定接觸(Bonded)限制軸向移動,仿真模型會由于泊松效應與邊緣效應影響接觸面的應力,在此選擇無分離接觸(No Separation)。仿真過程為了準確顯示模型的應力與變形,不施加外載荷及約束條件。
1.3 結果分析
外殼與軸承外圈應力、應變與變形云圖如圖4所示,與理論計算的對比見表3,誤差在允許范圍之內,說明理論分析的正確性。
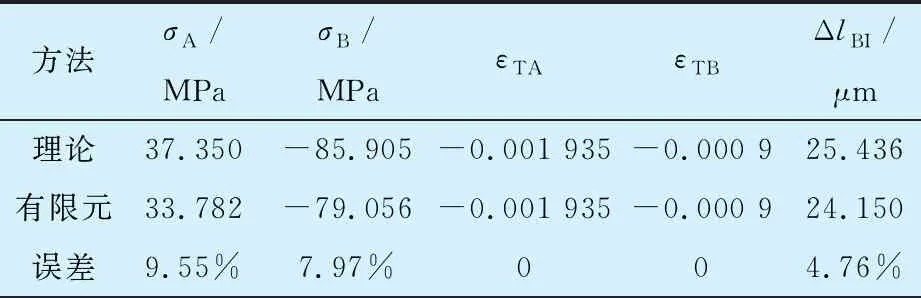
表3 外殼和軸承外圈應力、應變與變形的理論計算和有限元結果對比

圖4 外殼與軸承外圈應力、應變與變形云圖
分析可知:1)軸承外圈的徑向位移ΔlBI(軸承徑向游隙減少量)大于允許變化值(10~15 μm),軸承內部摩擦力矩增大,在小游隙組的情況下軸承可能卡死;2)軸承外圈在徑向受到89.042 MPa的正應力,反復的熱應力會加劇零件疲勞,降低軸承使用壽命。為減小極寒大溫差環境下溫差對軸承配合的影響,改善轉動關節的運動性能,提出一種可以減少配合零件在極寒大溫差環境下尺寸變化的自適應結構,并保持軸向預緊力不變,使軸承游隙在一定范圍內,從而提高運動精度并減少可能出現的摩擦力矩變化。
2 自適應結構
自適應結構如圖5所示,在關節中的布置圖如圖6所示(β為套筒頂角,取76°),功能實現原理如圖7所示,溫度變化時自適應結構可不斷循環調整,直至進入熱穩態。

圖5 自適應結構圖
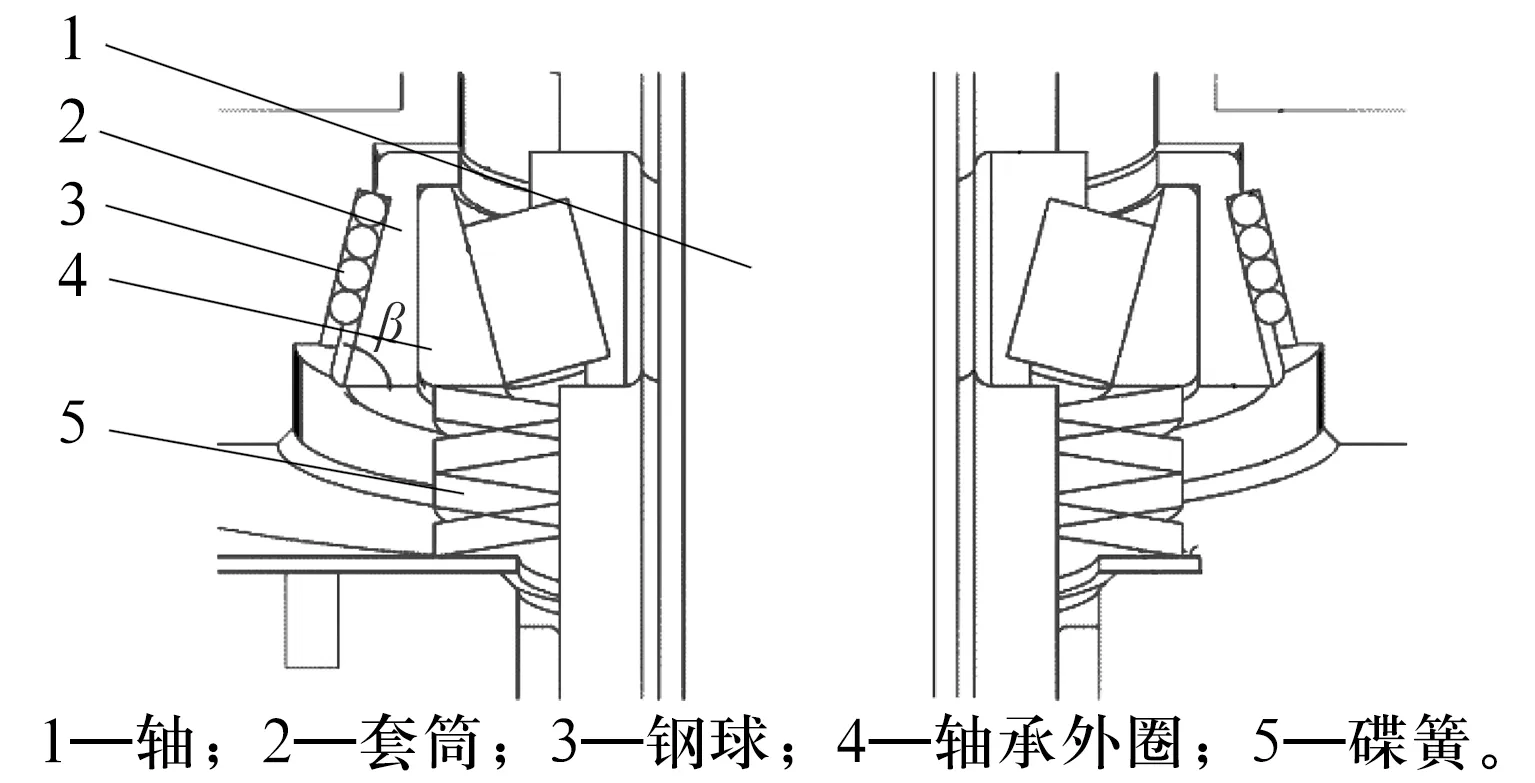
圖6 自適應結構在關節中的布置

圖7 自適應結構功能實現原理圖
自適應結構優點:1)外殼收縮受限而產生的熱應力轉化為斜向的壓力,推動圓錐滾子軸承外圈向外側移動,增大了外殼收縮所需的空間。同時,外圈向外側的移動可以消除溫度降低時軸承游隙的減小量。2)由于材料熱膨脹系數差異,溫度降低時套筒與外殼之間會產生間隙,利用彈簧壓緊套筒使其通過球始終與外殼接觸。3)套筒外側為帶有斜面的楔形圈,通過加載軸向彈力,使其達到徑向定壓預緊的效果,保證在大溫差環境中徑向載荷不變。
3 基于ADAMS仿真對結構有效性的驗證
基于ADAMS建立運動學仿真模型,驗證當溫度從22 ℃下降到-60 ℃時,自適應結構將熱效應產生的載荷轉化為動力,促使軸承外圈向外移動,從而增大軸承徑向游隙,消除因熱應力導致的軸承徑向游隙變化。
ADAMS無法模擬溫變過程中物體的變形,故將熱力耦合的復雜模型轉化為運動學模型,將自適應結構中鋼球徑向位移量設定為外殼徑向收縮量uA(0.045 477 mm)。如圖8所示,建立自適應結構ADAMS運動學模型,內圈及滾子固定,外圈沿軸向移動。對所有鋼球添加徑向的移動副并施加位移驅動,由于瞬時的熱應力極大,故采用STEP(time,0,0,8,0.045 477)函數控制運動時間及位移。在軸向添加剛度為200 N/mm的彈簧對外圈限位,防止模型由于約束不足一直運動。

圖8 自適應結構ADAMS運動學模型
軸承外圈軸向位移計算結果如圖9所示,最終位移量Δl為0.147 5 mm。當外圈向外側移動后,與外殼和軸承外圈相連接的鋼球會在凹槽內滾動并在新的位置維持平衡。由于軸承外圈背離外殼運動,徑向位移增加量ΔlBI=Δl/tanβ=0.036 7 mm,大于極寒大溫差環境下軸承外圈徑向總變形(0.024 15 mm),說明外殼在極寒大溫差環境下收縮變形不受約束,熱應力消失。新穩態時,在彈簧壓力作用下軸承外圈與外殼重新達到剛性連接狀態,維持了原有的游隙并消除熱應力。
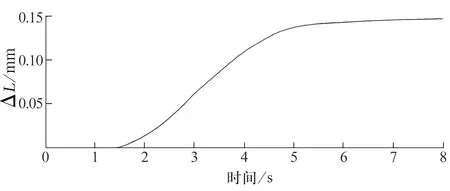
圖9 軸承外圈軸向位移仿真結果
4 結束語
通過對極寒大溫差環境下轉動關節處外殼和圓錐滾子軸承外圈應力、應變及變形的分析,設計了一種溫度自適應補償機構,該機構通過軸向定壓預緊,自動調節軸承徑向游隙,避免低溫下因配合間隙變小而產生的卡滯現象,提高了運動精度和傳動效率。

