一類帶有臨界指數的Schr?dinger-Poisson系統非平凡解的存在性

廖家鋒，朱麗君

(西華師范大學 a.數學與信息學院，b.公共數學學院，四川 南充 637009)

考慮如下帶有臨界指數的Schr?dinger-Poisson系統

(1)

其中η∈R{0},f∈C(R3×R,R),V滿足以下假設：

(V)V∈C(R3,R)，infV(x)≥a1>0且?M>0,meas{x∈R3∶V(x)≤M}<+∞，其中a1和meas分別表示一個實數和R3中的Lebesgue測度。

(F1) 對于任意的p∈(2,6)以及存在一個正實數C，使得?(x,s)∈R3×R,有

|f(x,s)|≤C(1+|s|p-1)；

(F3) 存在θ0∈(0,1)，使得對任意x∈R3,t>0以及τ≠0，有

受文獻[5-6]的啟發，本文將在(F3)條件下，利用變分法和山路引理研究系統(1)非平凡解的存在性問題。本文的主要結果如下：

定理1 假設η∈R{0}，(V)，(F1)-(F4)都成立， 則系統(1)至少存在一個非平凡解。

1 預備知識

本文將使用以下符號：

(2)

在不同行間，C表示不同的正實數。

由Lax-Milgram定理，對任意的u∈E，系統(1)中第二個方程有唯一解?u∈D1,2(R3)與之對應，將?u代入系統(1)的第一個方程，則系統(1)可轉換成如下方程

-Δu+V(x)u+η?uu=f(x,u)+u5。

(3)

方程(3)所對應的能量泛函I為

顯然，I∈C1(E,R)。眾所周知，方程(3)的弱解與能量泛函I的臨界點是一一對應的，且對任意的u,v∈E，有

由文獻[2]可知，系統(1)的解與泛函I在E中的臨界點是一一對應的。因此，證明系統(1)有非平凡解等價于證明泛函I有非平凡臨界點。

2 定理1的證明

由文獻[8]，可得一些關于?u的性質：

引理1 對于每個u∈E，都存在如下方程的唯一解?u∈D1,2(R3)：

-Δ?=u2,x∈R3，

且?u滿足以下性質：

(2)?u≥0且當u≠0時，有?u>0；

下面驗證泛函I在E中滿足山路結構。

引理2 假設η∈R{0}且(F1),(F2),(F4)都成立，且I(0)=0,

(a)存在ρ,α>0，使得當‖u‖=ρ時，有I(u)≥α；

(b)存在某個函數v∈E，滿足‖v‖>ρ，I(v)<0。

證明(a)由假設(F1)和(F2)，對于任意的ε>0，都存在Cε>0，使得

(4)

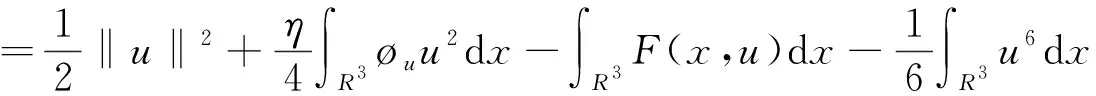
(b)固定u0∈E且u0≠0，令

由假設(F4)，對任意的M>0，存在RM>0，使得F(x,u)≥M|u|4,?|u|≥RM,x∈R3，再結合(4)式，有

|F(x,u)|≥M|u|4-CM|u|2, ?(x,u)∈R3×R3。

(5)

由(5)式，可得

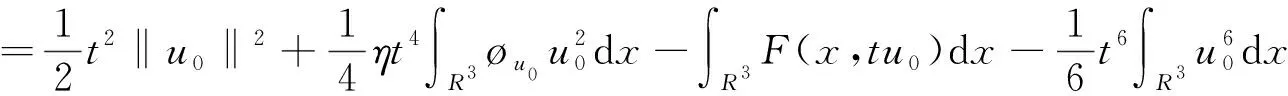
可推斷出，當t→+∞時，I(tu0)→-∞。于是，可選取一個足夠大的t*>0，使得‖t*u0‖>ρ并且I(t*u0)<0。故，令v=t*u0∈E且‖v‖>ρ，即有I(v)<0，因此(b)也得證。引理2證畢。

接下來，證明I在E中滿足局部的(PS)c條件。

證明假設{un}為泛函I在E中的(PS)c序列，則當n→∞時，有

(6)

首先，證明序列{un}在E中有界。由假設(F3)可得，對任意的x∈R3,t≥0,τ∈R，有

(7)

令(7)式中t=0，有

(8)

當n充分大時，由(6)式和(8)式，可以推得

這就意味著{un}在E中有界。令on(1)表示n→∞時的高階無窮小，從而存在子列{un}(此時不妨仍記為{un})以及u∈E，使得當n→∞時，有

(9)

接下來，記wn=un-u，由文獻[9-10]中的Brézis-Lieb引理，可得

‖un‖2=‖u‖2+‖wn‖2+on(1)，

(10)

(11)

由(4)式和Lebegue’s控制收斂定理，有

(12)

(13)

令(13)式中的φ=u，有

(14)

由(6)式有，〈I′(un),un〉→0,再結合(10)—(12)式以及引理1，可得

(15)

由(14)式和(15)式，有

(16)

一方面，根據(8)式和(14)式，可得

≥0。

(17)

另一方面，根據(6)式、(10)—(12)式和(16)式，可得

<0，

下面估計泛函I在E中山路水平值。

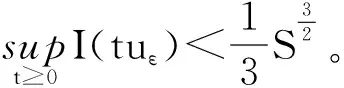
(18)

(19)

根據M的任意性可知，當M充分大時可以推得

引理4證畢。

下面，給出定理1的證明。

定理1的證明由引理2與文獻[11]中的山路引理，可知泛函I有山路幾何結構。定義