具有信號依賴靈敏度的趨化-趨觸模型解的第三個分量的衰減估計(jì)

劉 嬌，李中平

(西華師范大學(xué) 數(shù)學(xué)與信息學(xué)院，四川 南充 637009)

近年來，許多學(xué)者研究了關(guān)于腫瘤細(xì)胞侵入正常組織再生過程的數(shù)學(xué)模型[1-6]，Chaplain和Lolas[7]研究了如下恒定靈敏度的趨化-趨觸模型：

(1)

(2)

其中Ω是Rn(n≥3)中的一個有界光滑區(qū)域，υ是單位外法向量，ξ>0，μ>0，χ(v)是信號依賴靈敏度函數(shù)，u(x,t)、v(x,t)、w(x,t)分別代表了腫瘤細(xì)胞濃度、基質(zhì)降解酶濃度、細(xì)胞外基質(zhì)濃度。當(dāng)χ滿足如下條件

(3)

其中αp0是一個正常數(shù)，文獻(xiàn)[11]得到了模型(2)在n≥3時解的全局存在性和有界性。本文在此基礎(chǔ)上進(jìn)一步研究當(dāng)χ(v)滿足條件

(4)

(5)

接下來給出本文的主要結(jié)論：

1 基本引理

引理1 假設(shè)(u,v,w)是模型(2)的有界解，且(u0,v0,w0)滿足(5)，那么對于所有的t∈(0，T)都有

證明由模型(2)的第三個方程可得

(6)

其中x∈Ω,t∈(0,T)。所以有

(7)

根據(jù)不等式(x-y)2≤2(x2+y2)和應(yīng)用分部積分得

(8)

根據(jù)文獻(xiàn)[9]中推論3.3相同的方法得到了模型(2)中解的第二個分量v的下界估計(jì)。

引理3 假設(shè)(u,v,w)是模型(2)的解，對于任意的ε>0，當(dāng)t≥t1時，有

(9)

證明將模型(2)中第一個方程在Ω上積分并利用H?lder不等式得到

(10)

(11)

(12)

(13)

2 定理的證明

(14)

根據(jù)(8)(9)(12)得

因?yàn)閘nu(·,t)≤u(·,t)，所以有

由(11)得

(15)

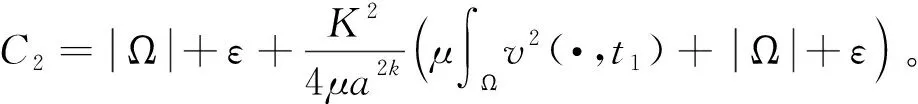
(16)

證明根據(jù)引理2和引理4得

(17)

根據(jù)(6)和(17)得

‖w(x,t)‖L∞(Ω)≤‖w0‖L∞(Ω)e-Γβt+ΓC′+C*=C3‖w0‖L∞(Ω)e-Γβt，

(18)

‖?w(x,t)‖L∞(Ω)≤‖?w0‖L∞(Ω)e-Γβt+ΓC′+C*+‖w0‖L∞(Ω)e-Γβt+ΓC′+C*Bt

(19)

‖w(·,t)‖W1,∞(Ω)≤Ce-γt。