存在設(shè)備時(shí)間限制的兩個(gè)企業(yè)協(xié)同的綜合調(diào)度算法
謝志強(qiáng) 裴莉榕
(哈爾濱理工大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院 哈爾濱 150080)
1 前言
隨著工業(yè)經(jīng)濟(jì)的發(fā)展,建設(shè)高水平開放式區(qū)域協(xié)同創(chuàng)新體系成為工業(yè)經(jīng)濟(jì)發(fā)展的重中之重。企業(yè)協(xié)同隨之成為企業(yè)發(fā)展必須解決的問(wèn)題。企業(yè)之間通過(guò)信息共享,從而實(shí)現(xiàn)加工任務(wù)在合作車間之間的相互協(xié)調(diào)和交換,從而相互代為完成加工任務(wù),使企業(yè)更大限度地完成一些不能獨(dú)立完成的任務(wù),最大限度地減少設(shè)備空閑時(shí)間,提高設(shè)備的使用率,提升企業(yè)收益,擴(kuò)大企業(yè)規(guī)模。為此,協(xié)同加工更符合現(xiàn)階段生產(chǎn)需求。關(guān)于車間調(diào)度問(wèn)題的研究,從車間類型分析,分為流水車間[1]和作業(yè)車間[2]。從車間數(shù)目分析,分為單車間和多車間[3]。從加工設(shè)備屬性分析,分為柔性車間[4–6]和非柔性車間。從目標(biāo)數(shù)量分析,分為單目標(biāo)和多目標(biāo)[7–9]。隨著產(chǎn)品復(fù)雜度變高,單車間制造已經(jīng)無(wú)法滿足現(xiàn)階段的需求。為此,在單車間調(diào)度的基礎(chǔ)上,眾多學(xué)者對(duì)多車間以及分布式車間制造進(jìn)行了深入的研究,并取得了相應(yīng)的成果[10–15]。
以上這些研究都是將產(chǎn)品分化成零部件,將零部件進(jìn)行分批次加工,加工完成后再進(jìn)行組裝,屬于流水線工程,并沒有考慮針對(duì)于單件復(fù)雜產(chǎn)品加工時(shí),工序之間存在約束關(guān)系,將加工和裝配并行進(jìn)行,從而實(shí)現(xiàn)縮短加工時(shí)間以及減少加工成本,提升產(chǎn)品的生產(chǎn)效率。于是,謝志強(qiáng)等人[16–19]提出了一系列綜合調(diào)度問(wèn)題。關(guān)于綜合調(diào)度問(wèn)題的研究,從產(chǎn)品角度分析,包含一般產(chǎn)品綜合調(diào)度問(wèn)題和特殊產(chǎn)品綜合調(diào)度問(wèn)題。一般產(chǎn)品綜合調(diào)度問(wèn)題又分為單產(chǎn)品綜合調(diào)度問(wèn)題、多產(chǎn)品小批量綜合調(diào)度問(wèn)題。特殊產(chǎn)品綜合調(diào)度問(wèn)題分為工序緊密銜接調(diào)度問(wèn)題和工序非緊密銜接調(diào)度問(wèn)題。以上對(duì)于綜合調(diào)度的研究大部分為單一企業(yè)內(nèi)部車間問(wèn)題,也就是一個(gè)企業(yè)內(nèi)工件在單個(gè)車間或多個(gè)車間進(jìn)行加工引發(fā)的一系列問(wèn)題。文獻(xiàn)[20]提出的基于混合教學(xué)優(yōu)化算法的多車間協(xié)作綜合調(diào)度,雖然提出了車間協(xié)作問(wèn)題,但只考慮多車間設(shè)備集的交集部分且對(duì)于遷移問(wèn)題的考慮固定且單一,并沒有實(shí)質(zhì)上的解決車間協(xié)作的問(wèn)題。而針對(duì)企業(yè)車間協(xié)同問(wèn)題研究較少,企業(yè)協(xié)同主要是分為兩種,一種是自有加工企業(yè)設(shè)備使用時(shí)間存在限制,導(dǎo)致加工任務(wù)不能如期完成;另一種是存有特殊工序在特殊設(shè)備上進(jìn)行加工,自有加工企業(yè)缺少該工序所需加工設(shè)備。上述兩種情況使得自有加工企業(yè)都必須尋求其他加工企業(yè)進(jìn)行輔助加工,從而完成加工任務(wù)。而在實(shí)際生產(chǎn)過(guò)程中,由于加工設(shè)備的定期維護(hù)會(huì)出現(xiàn)設(shè)備的正常使用時(shí)間存在極大的限制。因此,提出的存在設(shè)備時(shí)間限制的兩個(gè)企業(yè)協(xié)同的綜合調(diào)度算法即是針對(duì)企業(yè)車間協(xié)同問(wèn)題中自有加工企業(yè)設(shè)備使用時(shí)間存在限制的綜合調(diào)度問(wèn)題進(jìn)行進(jìn)一步的分析和研究。設(shè)計(jì)加工任務(wù)分配策略保證了自有加工企業(yè)獲得更多的收益,設(shè)計(jì)原加工企業(yè)工序車間選擇策略和協(xié)同選擇策略,在考慮到運(yùn)輸問(wèn)題并滿足交貨期的前提下選取獲得收益更大的協(xié)同加工企業(yè)。經(jīng)過(guò)實(shí)例分析,該算法可以更好地解決加工企業(yè)由于設(shè)備使用時(shí)間的限制并帶有交貨期和收益的企業(yè)車間協(xié)同綜合調(diào)度問(wèn)題。
2 問(wèn)題描述分析
綜合調(diào)度問(wèn)題既不僅考慮了產(chǎn)品的加工問(wèn)題,同時(shí)也考慮了產(chǎn)品的裝配問(wèn)題。在實(shí)際的生產(chǎn)中,通過(guò)企業(yè)之間的信息共享,實(shí)現(xiàn)產(chǎn)品加工任務(wù)在合作車間之間的相互協(xié)調(diào)和交換,相互代為完成任務(wù)。協(xié)同加工不僅能夠減少設(shè)備空閑時(shí)間,提高設(shè)備的使用率,同時(shí)能夠提升企業(yè)的經(jīng)濟(jì)效益并增大企業(yè)收益。協(xié)同加工通常是由兩種情況引起的,一種是自有加工企業(yè)設(shè)備使用時(shí)間存在限制,導(dǎo)致加工任務(wù)不能在交貨期內(nèi)完成;另一種是存有特殊工序需要在特殊設(shè)備上進(jìn)行加工,自有加工企業(yè)不存在該工序所需加工設(shè)備,這兩種情況使得自有加工企業(yè)都必須尋求其他加工企業(yè)輔助加工,從而完成加工任務(wù)。協(xié)同加工以往的模式是將企業(yè)任務(wù)信息,設(shè)備信息等所有信息集中處理,進(jìn)行資源優(yōu)化。但是這種方式數(shù)據(jù)量過(guò)于龐大并且在處理數(shù)據(jù)的過(guò)程中由于冗長(zhǎng)的環(huán)節(jié)致使企業(yè)信息泄露對(duì)企業(yè)造成不可估量的損失。為此,提出存在設(shè)備時(shí)間限制的兩個(gè)企業(yè)協(xié)同的綜合調(diào)度算法需要滿足以下要求:
(1)訂單共享中心的任務(wù)不強(qiáng)制分配給各加工企業(yè),各加工企業(yè)可自由選擇。
(2)各加工企業(yè)提交協(xié)同意向后,并不表示合作達(dá)成。需要協(xié)同分配中心確定并簽訂合作達(dá)成意向書后,方可證明合作成功。
(3)任務(wù)共享中心中的任務(wù)會(huì)隨時(shí)更新,但達(dá)成協(xié)議的任務(wù)不可毀約,協(xié)議達(dá)成立刻生效。
(4)因兩個(gè)加工企業(yè)間協(xié)同任務(wù)引起的運(yùn)輸費(fèi)用,由兩個(gè)加工企業(yè)協(xié)商決定分配比例。
(5)現(xiàn)以最理想的模式分析,運(yùn)輸所消耗的時(shí)間和成本固定且模式單一,不會(huì)受到外界環(huán)境影響。
(6)由于是協(xié)同合作,所以各加工企業(yè)不可能存在無(wú)限制的加工,各加工企業(yè)車間設(shè)備加工有時(shí)限。
(7)各協(xié)同加工企業(yè)達(dá)成協(xié)議之后,必須按照其限定時(shí)間內(nèi)完成加工,不受其他因素影響。
(8)各加工企業(yè)設(shè)備屬性值均在正常范圍內(nèi),不會(huì)出現(xiàn)超負(fù)載或損壞等問(wèn)題。
(9)各加工企業(yè)設(shè)備為非柔性設(shè)備,加工工序和設(shè)備型號(hào)為一對(duì)一的關(guān)系。
(10)企業(yè)內(nèi)部各加工工序在各設(shè)備間移動(dòng)所消耗的時(shí)間和費(fèi)用存在且固定不變。
(11)加工工序之間存在工藝約束,必須在其緊前工序全部加工完成后方可加工。
(12)設(shè)備在加工過(guò)程中不存在臨時(shí)插入,必須加工完當(dāng)前工序方可加工下一道工序。
(13)產(chǎn)品加工完成之后,直接送往管理中心,運(yùn)輸費(fèi)用由自有加工企業(yè)承擔(dān)。
利用數(shù)學(xué)的方式描述該調(diào)度問(wèn)題,對(duì)所有相關(guān)的變量進(jìn)行如下定義:
J表示所有工序即工序集,單件復(fù)雜產(chǎn)品存在n道工序,J=J1,J2,···,Jn。
B表示所有加工車間即車間集,共存在L個(gè)車間,B=B1, B2,···,BL。
存在設(shè)備時(shí)間限制的兩個(gè)企業(yè)協(xié)同的綜合調(diào)度算法的目標(biāo)函數(shù)可定義為
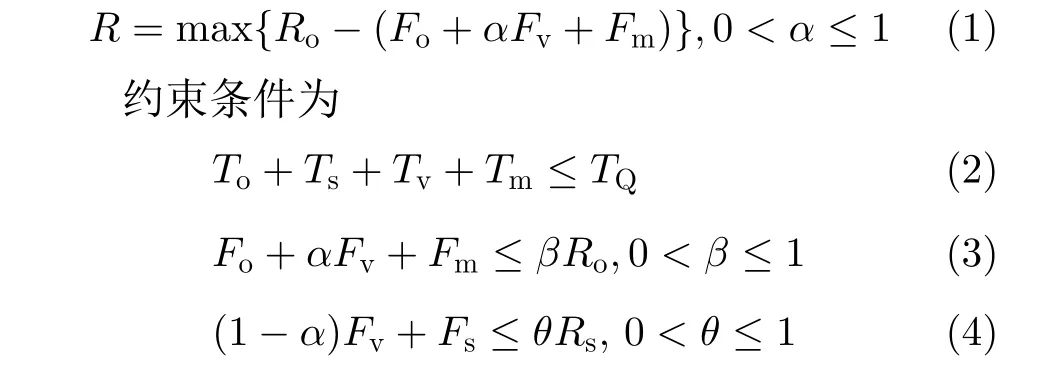
其中,式(1)表示自有加工企業(yè)在該任務(wù)中獲得的最終收益。式(2)表示的是交貨期約束。式(3)和式(4)分別表示自有加工企業(yè)和協(xié)同加工企業(yè)的收益約束,各參數(shù)含義如表1所示。

表1 各參數(shù)含義
3 算法詳細(xì)設(shè)計(jì)
近年來(lái)由于協(xié)同算法的提出,如何在保證商業(yè)信息安全的前提下,將不同區(qū)域內(nèi)的加工企業(yè)建立合作并合理地分配加工任務(wù),使企業(yè)獲得更多的收益成了解決問(wèn)題的關(guān)鍵,且該算法不受企業(yè)規(guī)模所影響。其主要步驟如下:
(1)需要自有加工企業(yè)將邊際收益較低的任務(wù)或是不可獨(dú)立完成的任務(wù)發(fā)送到任務(wù)共享中心。
(2)設(shè)備存在閑置的企業(yè)根據(jù)任務(wù)共享中心的信息提出協(xié)同意向及自身加工車間現(xiàn)況以及物流等信息。
(3)協(xié)同分配中心將各加工企業(yè)的協(xié)同意向進(jìn)行合并處理,整理出方案列表,并反饋給自有加工企業(yè)。
(4)自有加工企業(yè)根據(jù)方案列表中的信息,選取心儀的方案,并確定合作意向,并將合作意向反饋給協(xié)同分配中心。
(5)協(xié)同分配中心確定雙方合作意向達(dá)成。并回到步驟(2),直至所有任務(wù)最終分配完畢。
3.1 加工任務(wù)拆分策略
為了保證自有加工企業(yè)能夠獲得更多的收益,需要將加工任務(wù)盡可能多的分配給自有加工企業(yè)進(jìn)行加工,因此,需要將加工任務(wù)進(jìn)行有效分解并設(shè)計(jì)了加工任務(wù)分配策略。加工任務(wù)分配策略主要分為初始拆分和拆分調(diào)整兩大步驟,以圖1加工樹為例對(duì)其進(jìn)行初始拆分。節(jié)點(diǎn)信息為工序號(hào)/設(shè)備號(hào)/加工時(shí)長(zhǎng)(h)。
圖1中箭頭所指方向?yàn)樵摴ば虻木o后工序,以往的計(jì)算路徑長(zhǎng)度的方式都是從根節(jié)點(diǎn)開始,計(jì)算根節(jié)點(diǎn)到該節(jié)點(diǎn)的路徑長(zhǎng)度為該節(jié)點(diǎn)的路徑長(zhǎng)度值。采用逆向思維方式進(jìn)行剪枝從而生成初始拆分樹,具體步驟如下:
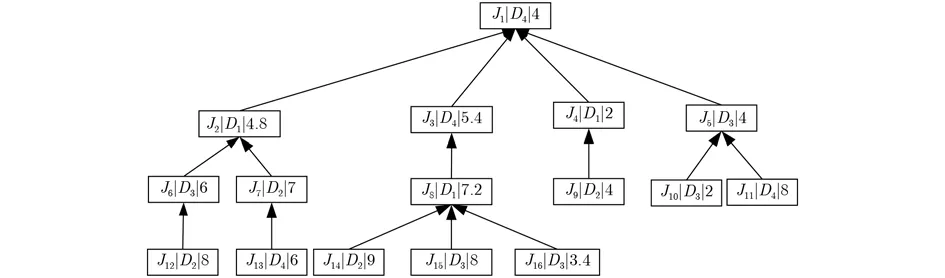
圖1 加工樹例1
(1)輸入加工樹中各節(jié)點(diǎn)信息。
(2)標(biāo)記各節(jié)點(diǎn)層數(shù)。加工樹共有C層,根節(jié)點(diǎn)層數(shù)為1,依次遞增,最后1層層數(shù)為C,按層遍歷加工樹。
(3)判斷該工序是否有緊前工序,若不存在緊前工序跳到步驟(4)。若存在緊前工序跳到步驟(5)。
(4)計(jì)算各工序路徑長(zhǎng)度,路徑長(zhǎng)度=max{緊前工序路徑長(zhǎng)度+當(dāng)前工序加工時(shí)長(zhǎng)}。
(5)標(biāo)記各工序路徑長(zhǎng)度。
(6)判斷加工樹中是否存在未標(biāo)記工序,若是轉(zhuǎn)到步驟(3),若否轉(zhuǎn)到步驟(7)。
(7)按后序遍歷的方式將加工樹中路徑長(zhǎng)度小于設(shè)備時(shí)限的工序進(jìn)行剪枝。
(8)建立虛擬根節(jié)點(diǎn),將剪枝下的工序重新構(gòu)建成一棵加工樹,即初始拆分樹。
按照初始拆分的步驟,首先逆向計(jì)算各工序的路徑長(zhǎng)度,并進(jìn)行標(biāo)記,如圖2所示。以工序J8為例,工序J8存在3個(gè)緊前工序,最大緊前工序路徑長(zhǎng)度與自身加工時(shí)間加和結(jié)果為J8的路徑長(zhǎng)度。以加工時(shí)長(zhǎng)為13作為設(shè)備加工時(shí)限,將所有路徑長(zhǎng)度小于13的工序和子樹進(jìn)行剪枝。帶虛線的工序?yàn)楸患舻舻墓ば颉?/p>
將圖2中虛線圈出的工序進(jìn)行剪枝,然后建立虛擬跟節(jié)點(diǎn),構(gòu)建拆分樹,生成初始拆分樹,如圖3所示。
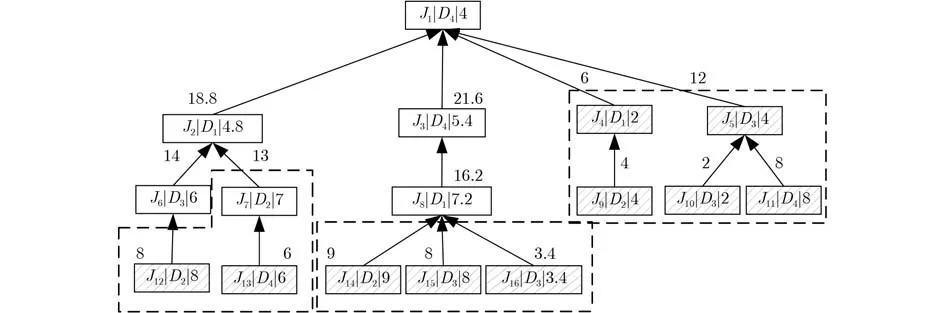
圖2 標(biāo)記加工樹
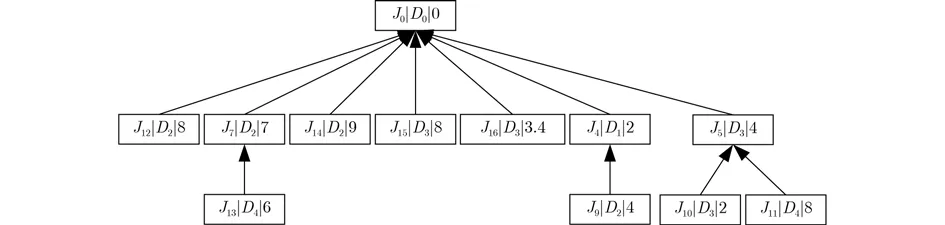
圖3 初始拆分樹
在實(shí)際調(diào)度過(guò)程中設(shè)備總時(shí)長(zhǎng)會(huì)受工序中關(guān)系約束和遷移約束影響且加工設(shè)備存在時(shí)間限制,所以首次拆分后產(chǎn)生的初始拆分樹在實(shí)際操作過(guò)程中,并不一定能夠滿足時(shí)間限制約束。因此需要對(duì)拆分樹中的工序進(jìn)行調(diào)整,在對(duì)初始拆分樹進(jìn)行微調(diào)整的過(guò)程中,需要對(duì)樹中各工序確定加工車間。判斷是否存在超時(shí)工序,若存在超時(shí)的工序,將超時(shí)工序從拆分樹中刪除,并添加到協(xié)同加工樹中。由于初始拆分樹是從自有加工工藝樹剪枝后合成的,所以存在純?nèi)~子節(jié)點(diǎn),即該工序不存在緊前工序且優(yōu)先級(jí)值為1。
3.2 原加工企業(yè)車間選擇策略
可調(diào)度工序存在緊前工序和緊后工序,由于存在多個(gè)車間且每個(gè)車間包含的加工設(shè)備型號(hào)不一致,將所有設(shè)備統(tǒng)一在一起,計(jì)算各型號(hào)設(shè)備個(gè)數(shù),存在個(gè)數(shù)為1的設(shè)備,標(biāo)記為特殊設(shè)備,當(dāng)存在工序加工設(shè)備為特殊設(shè)備時(shí),標(biāo)記Di=1,否則為0。用二進(jìn)制形式標(biāo)記各工序加工設(shè)備所在車間,假設(shè),存在3個(gè)車間B1,B2,B3,車間B1包含設(shè)備D1,D2,D4,車間B2包含設(shè)備D2,D3,車間B3包含設(shè)備D3,D4,工序i可以在設(shè)備D3上加工。則用二進(jìn)制表示為011。若其緊后工序i+1所用設(shè)備為D2,則用二進(jìn)制表示為110,將兩者進(jìn)行“&”運(yùn)算得出結(jié)果為010,可以確定可共用車間為B2。工序車間選擇具體步驟如下:
(1)將初始拆分樹中非純?nèi)~子節(jié)點(diǎn)的各工序信息輸入。
(2)用二進(jìn)制形式標(biāo)記各工序加工設(shè)備所在車間,并對(duì)在特殊設(shè)備上加工的工序標(biāo)記Di=1。
(4)建立虛擬加工工序,模擬工序遷移情況,并計(jì)算工序在其加工設(shè)備所在車間的最早開始時(shí)間,若最早開始時(shí)間相同轉(zhuǎn)到步驟(5),若最早開始時(shí)間不相同,選取最早開始時(shí)間最早的車間,轉(zhuǎn)到步驟(8)。
(5)查看該工序緊后工序二進(jìn)制值進(jìn)行“&”運(yùn)算,確定結(jié)果為1的車間,并記錄車間數(shù)CB。
(6)判斷CB值是否為1。若為1,將該工序安排在該加工車間,轉(zhuǎn)到步驟(8),若不為1,轉(zhuǎn)到步驟(7)。
(7)判斷不同車間內(nèi)該工序所需設(shè)備上的空閑時(shí)間段,選取空閑時(shí)間段小的車間。
(8)將該工序從工序集中刪除,判斷工序集是否為空,若工序集為空,輸出甘特圖,轉(zhuǎn)到步驟(9),若工序集不為空,轉(zhuǎn)到步驟(3)。
(9)將補(bǔ)入集中純?nèi)~子節(jié)點(diǎn)輸入,查找空閑時(shí)間段,利用考慮無(wú)縫拉伸的多設(shè)備緊湊優(yōu)化調(diào)度策略將純?nèi)~子工序插入。
(10)判斷插入后是否超時(shí),若不超時(shí),轉(zhuǎn)到步驟(11),若超時(shí),轉(zhuǎn)到步驟(12)。
傳統(tǒng)制造業(yè)習(xí)慣于在遇到管理問(wèn)題時(shí),通過(guò)成立專門應(yīng)對(duì)部門的方法來(lái)解決,這就導(dǎo)致各個(gè)層級(jí)的管理部門越來(lái)越多,組織機(jī)構(gòu)錯(cuò)綜復(fù)雜,管理權(quán)限界定不明確,往往老的問(wèn)題還沒有解決,新的衍生問(wèn)題又浮出水面。
(11)輸出該工序。
(12)從補(bǔ)入集中刪除該工序,判斷補(bǔ)入集是否為空,若為空,轉(zhuǎn)到步驟(13),若不為空,轉(zhuǎn)到步驟(9)。
(13)輸出甘特圖,結(jié)束。
3.3 協(xié)同車間選擇策略
對(duì)于每個(gè)企業(yè)來(lái)說(shuō),可以將邊際效益低或無(wú)法獨(dú)自加工完成的任務(wù)發(fā)送到共享中心中尋找協(xié)同企業(yè)進(jìn)行加工合作,掙取對(duì)應(yīng)收益,而自身獲取收益的高低則是選擇合作伙伴的關(guān)鍵。由此,對(duì)于協(xié)同任務(wù)的分析變得尤為重要。加工樹經(jīng)過(guò)拆分后生成自有加工企業(yè)加工的拆分加工樹,而其余部分為協(xié)同加工企業(yè)加工的協(xié)同加工樹。為了使自有加工企業(yè)在滿足交貨期的前提下,獲取最大的收益,需要對(duì)協(xié)同加工樹分析,確定協(xié)同加工企業(yè)所需設(shè)備的最低要求,以及在存在運(yùn)輸問(wèn)題的情況下,加工任務(wù)能夠在交貨期內(nèi)完成。主要從以下4個(gè)點(diǎn)進(jìn)行分析,設(shè)備型號(hào)、協(xié)同車間最大加工時(shí)間、設(shè)備數(shù)、收益。詳細(xì)流程圖如圖4所示。
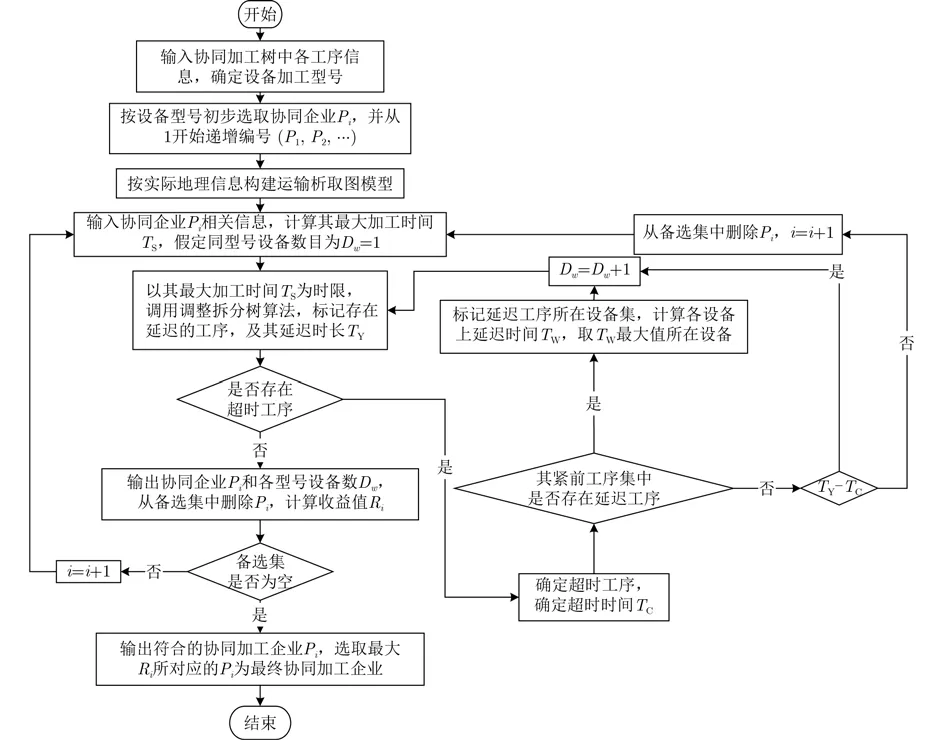
圖4 協(xié)同選擇策略流程
(1)設(shè)備型號(hào)是根據(jù)協(xié)同加工樹中各節(jié)點(diǎn)信息確定協(xié)同車間需要的設(shè)備型號(hào)。
(2)協(xié)同車間最大加工時(shí)間是根據(jù)各企業(yè)之間的實(shí)際地理位置建立數(shù)據(jù)庫(kù),確定運(yùn)輸時(shí)間Tv以及協(xié)同車間到管理中心的時(shí)間Tm,由于拆分樹已知,且在拆分樹調(diào)整過(guò)程中便可得到對(duì)應(yīng)的甘特圖,從而得到原加工車間加工時(shí)間To,利用公式Ts= TQ–(To+Tv+Tm),得到協(xié)同車間最大加工時(shí)間Ts。
(3)設(shè)備數(shù)是假定同型號(hào)設(shè)備數(shù)目為Dw=1,w表示型號(hào)標(biāo)號(hào),以協(xié)同車間最大加工時(shí)間Ts為時(shí)間限制,調(diào)用拆分樹調(diào)整算法對(duì)協(xié)同加工樹進(jìn)行分析,標(biāo)記存在延遲的工序,判斷是否存在工序加工時(shí)間超過(guò)Ts。對(duì)超過(guò)Ts工序及其緊前工序集中發(fā)生延遲的工序時(shí)長(zhǎng)進(jìn)行分析,尋找對(duì)應(yīng)型號(hào)設(shè)備并將設(shè)備數(shù)目加1,輸出各型號(hào)設(shè)備數(shù)。假定工序J1的緊前工序?yàn)镴2,J3,工序J2的緊前工序?yàn)镴4,存在3種型號(hào)設(shè)備D1,D2,D3。
假定工序調(diào)度后的甘特圖如圖5中下半部分,虛線為時(shí)間線,當(dāng)工序J1超時(shí),首先判斷超時(shí)工序是否為延遲工序。J1為延遲工序。增加該工序所用設(shè)備,重新調(diào)度判斷是否超時(shí),圖例中剛好未超時(shí)。假若重新調(diào)節(jié)后工序仍然超時(shí),判斷其緊前工序集中工序所在設(shè)備是否需要增加,如圖6所示。J1仍為超時(shí),查詢延遲時(shí)間最大設(shè)備,增加該設(shè)備數(shù),新調(diào)度判斷是否超時(shí),直到不存在超時(shí)工序或不存在延遲時(shí)間。
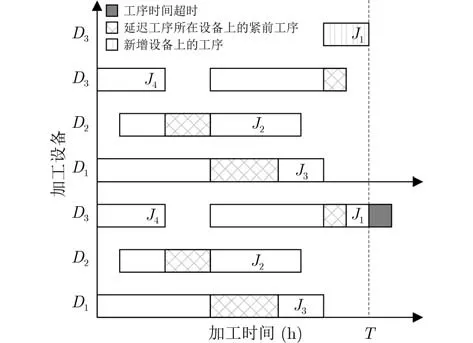
圖5 協(xié)同加工樹調(diào)度甘特圖
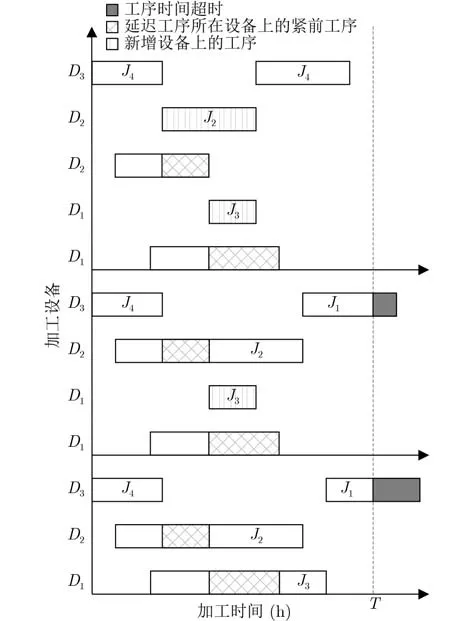
圖6 增加設(shè)備后對(duì)比甘特圖
(4) 收益是由于各車間情況基本確定,且對(duì)應(yīng)的運(yùn)輸情況也已知,便可以獲得相關(guān)費(fèi)用信息,利用公式R=Ro–(Fo+αFv+Fm)確定不同企業(yè)協(xié)同合作下的收益,最終以收益最大值為協(xié)同加工企業(yè)。
4 實(shí)例分析
算法可以用于復(fù)雜的單產(chǎn)品,為了便于理解,實(shí)例用較為簡(jiǎn)單的產(chǎn)品工藝樹進(jìn)行分析。模擬其中數(shù)據(jù)并以圖7所示加工樹為實(shí)例,圖中工序信息為工序號(hào)、設(shè)備號(hào)、加工時(shí)長(zhǎng)。從葉子節(jié)點(diǎn)開始,逆向計(jì)算各工序路徑長(zhǎng)度,假定以時(shí)長(zhǎng)20 h為限,對(duì)加工樹進(jìn)行剪枝,如圖8所示。
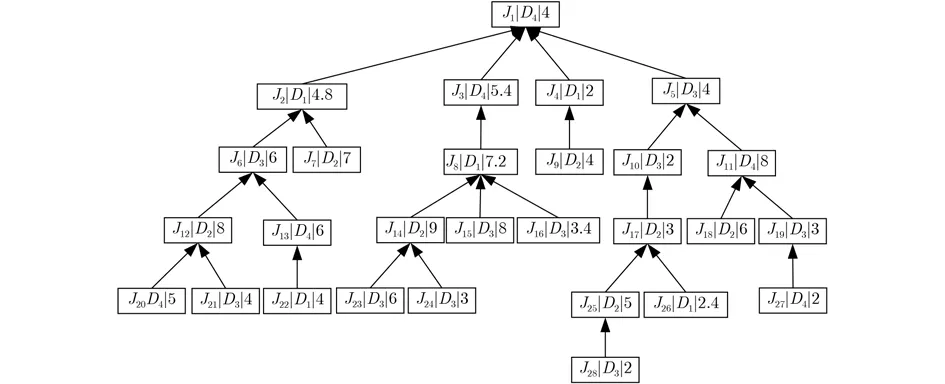
圖7 加工樹實(shí)例
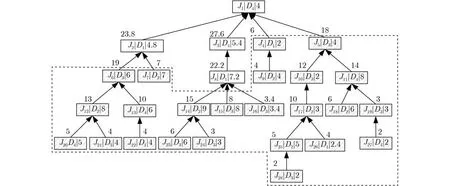
圖8 標(biāo)記加工樹
構(gòu)建虛擬根節(jié)點(diǎn),將剪枝下的樹和節(jié)點(diǎn)中不存在緊后工序的節(jié)點(diǎn)與根節(jié)點(diǎn)建立連接,如圖9所示。
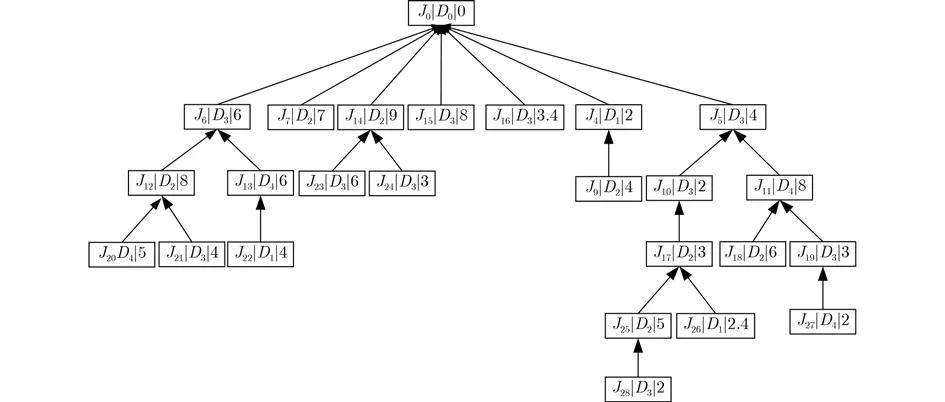
圖9 初始拆分樹

從根節(jié)點(diǎn)開始,正序計(jì)算各工序路徑長(zhǎng)度并標(biāo)記其層數(shù),不存在緊前工序的節(jié)點(diǎn)為葉子節(jié)點(diǎn)。將不存在緊前工序且層數(shù)為1 的純?nèi)~子節(jié)點(diǎn)即{J7,J15,J16}放入補(bǔ)入集。如圖10所示,深灰色填充的工序?yàn)榧內(nèi)~子節(jié)點(diǎn)。將除純?nèi)~子節(jié)點(diǎn)以外的葉子節(jié)點(diǎn)工序放入工序集。虛線畫出的節(jié)點(diǎn)為葉子節(jié)點(diǎn)。
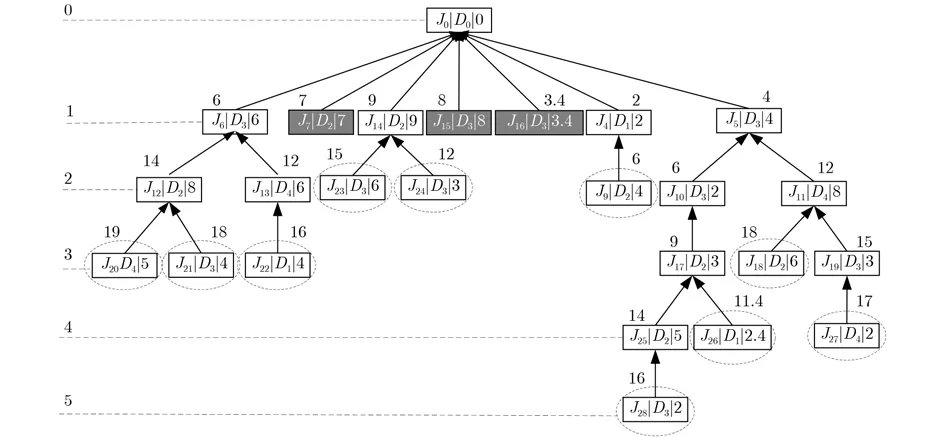
圖10 標(biāo)記初始拆分樹
得到工序集{J28,J27,J26,J24,J23,J22,J21,J20,J18,J9},路徑值最大工序?yàn)镴20,路徑長(zhǎng)度為19,加工設(shè)備為D4,設(shè)備對(duì)應(yīng)工序備選集為{J27,J20},最大層數(shù)工序?yàn)镴27,輸出J27,設(shè)備D4為特殊設(shè)備,將工序J27安排在車間B2中,記錄開始時(shí)間和結(jié)束時(shí)間(0 ,2),將J27從工序集合備選集中刪除,產(chǎn)生新葉子節(jié)點(diǎn)工序J19,設(shè)備為D3,將工序J19加入工序集,工序J20未輸出,備選集中工序?yàn)閧J20},個(gè)數(shù)為1,直接分配J20車間為B2,記錄開始時(shí)間和結(jié)束時(shí)間(2,7),將J20從工序集和備選集中刪除,備選集中工序個(gè)數(shù)為0。不斷更新循環(huán)得到的甘特圖如圖11所示。輸入補(bǔ)入集工序{J7,J15,J16},工序J7所用設(shè)備為D2,工序(J15,J16)所用設(shè)備為D3,利用無(wú)縫拉伸的多設(shè)備緊湊優(yōu)化調(diào)度思想,將工序{J7,J15,J16}按加工時(shí)長(zhǎng)依次插入,插入后未發(fā)生超時(shí),插入后甘特圖如圖12所示。
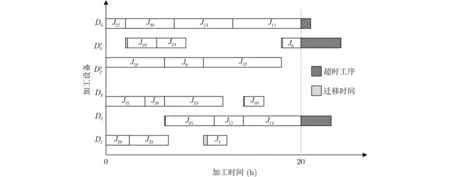
圖11 初始拆分樹調(diào)度發(fā)生超時(shí)甘特圖
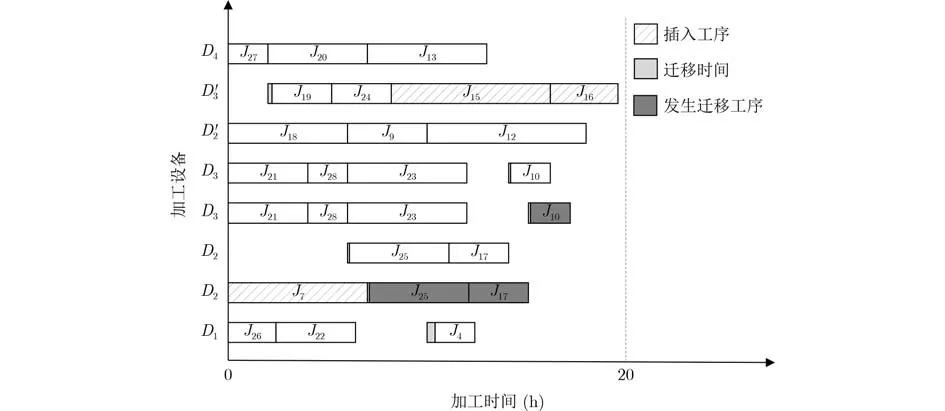
圖12 純?nèi)~子節(jié)點(diǎn)插入后對(duì)比甘特圖
文獻(xiàn)[17]中涉及交貨期問(wèn)題,但針對(duì)的是多產(chǎn)品小批量問(wèn)題,基于此,假定產(chǎn)品優(yōu)先級(jí)為1,遷移時(shí)間同表2所示,閾值仍為20,利用文獻(xiàn)[17]中的算法調(diào)度后的甘特圖如圖13所示。通過(guò)計(jì)算可知,算法在閾值內(nèi)可加工20道工序,加工總時(shí)長(zhǎng)為85.8 h,而文獻(xiàn)[17]中的算法在閾值內(nèi)可加工14道工序,加工總時(shí)長(zhǎng)為65.8 h,相差6道工序和20 h。對(duì)比結(jié)果可得,算法對(duì)于求解加工企業(yè)設(shè)備使用時(shí)間存在限制并帶有交貨期和收益的企業(yè)車間協(xié)同綜合調(diào)度問(wèn)題能夠得到優(yōu)良結(jié)果。說(shuō)明了算法的有效性,相較已有文獻(xiàn)[12]中的算法具有一定的優(yōu)越性。針對(duì)協(xié)同加工樹進(jìn)行分析確定加工設(shè)備型號(hào)。經(jīng)過(guò)調(diào)節(jié)后,最終形成的協(xié)同加工樹,協(xié)同加工樹仍然需要4種型號(hào)設(shè)備D1,D2,D3,D4,利用長(zhǎng)路徑、層優(yōu)先和短用時(shí)策略對(duì)協(xié)同加工樹進(jìn)行調(diào)度,形成圖14所示甘特圖。
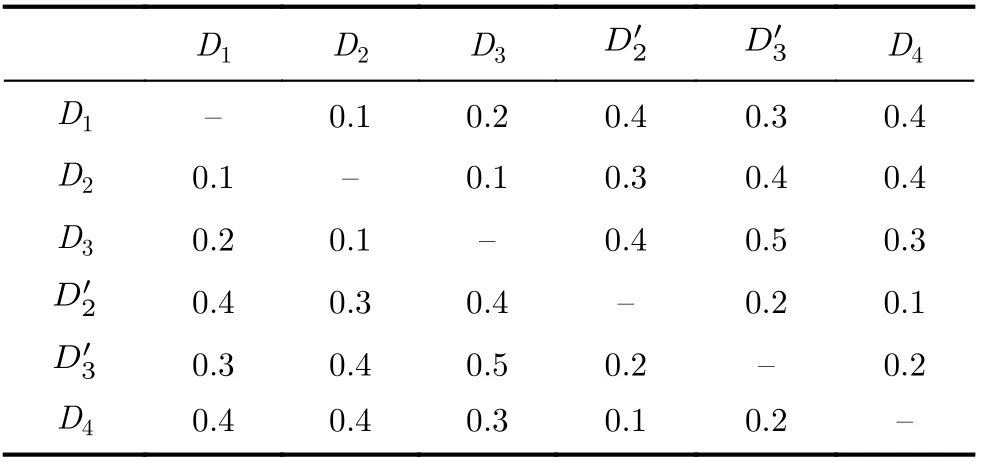
表2 企業(yè)內(nèi)部設(shè)備遷移信息 (h)
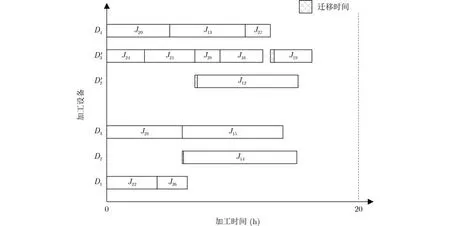
圖13 文獻(xiàn)[17]調(diào)度甘特圖
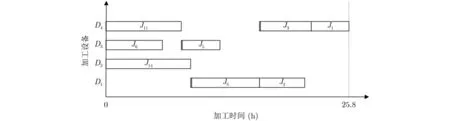
圖14 協(xié)同加工樹調(diào)度甘特圖
假定交貨期TQ=60,利用協(xié)同選擇策略發(fā)現(xiàn)存在3家企業(yè)符合要求,時(shí)間未超過(guò)交貨期,由于圖例較為簡(jiǎn)單,恰好未存在延遲工序且不存在超時(shí)現(xiàn)象,故不存在可增加設(shè)備,只需考慮運(yùn)輸問(wèn)題。假定3家符合條件的協(xié)同企業(yè)P1,P2,P3,相關(guān)信息如表3所示。

表3 協(xié)同加工企業(yè)相關(guān)信息
假定α取值為0.5(具體取值根據(jù)實(shí)際合約情況決定),Ro=150,Fo=50,To=19.6。利用公式R=Ro–(Fo+αFv+Fm)和TQ=To+Ts+Tv+Tm計(jì)算得到如下結(jié)果:R1=80.0, T1=54.9, R2=82.25,T2=56.5, R3=81.91, T3=58。由此可以看出,在未超過(guò)交貨期的前提下,盈利最多的是P2,故選擇協(xié)同加工企業(yè)P2進(jìn)行合作。
5 結(jié)束語(yǔ)
(1) 相比以往的研究,本文首次提出解決兩個(gè)企業(yè)車間協(xié)同合作問(wèn)題的方法,通過(guò)對(duì)比收益值能夠更加直觀反應(yīng)企業(yè)收益。較比單一多車間加工與單一分布式車間加工的加工方式,協(xié)同加工合作能為加工企業(yè)取得更多的盈利。
(2) 將工序在多車間遷移問(wèn)題和產(chǎn)品在兩車間的運(yùn)輸問(wèn)題以具體數(shù)值進(jìn)行分析,提高了結(jié)果準(zhǔn)確性。
因此,提出的存在設(shè)備時(shí)間限制的兩個(gè)企業(yè)協(xié)同的綜合調(diào)度算法,可以更好解決加工企業(yè)設(shè)備使用時(shí)間存在限制并帶有交貨期和收益的企業(yè)車間協(xié)同綜合調(diào)度問(wèn)題,使企業(yè)更大限度地完成一些不能獨(dú)立完成的任務(wù),最大限度地減少設(shè)備空閑時(shí)間,提高設(shè)備的使用率,提升企業(yè)收益,擴(kuò)大企業(yè)規(guī)模。對(duì)企業(yè)協(xié)同綜合調(diào)度問(wèn)題的進(jìn)一步研究具有一定的意義。
- 電子與信息學(xué)報(bào)的其它文章
- 基于加權(quán)核范數(shù)和L2,1范數(shù)的最優(yōu)均值線性分類器
- 復(fù)雜場(chǎng)景點(diǎn)云數(shù)據(jù)的6D位姿估計(jì)深度學(xué)習(xí)網(wǎng)絡(luò)
- 基于改進(jìn)Res-UNet網(wǎng)絡(luò)的鋼鐵表面缺陷圖像分割研究
- 基于寬度學(xué)習(xí)的注塑產(chǎn)品質(zhì)量預(yù)測(cè)方法
- 考慮工序序列動(dòng)態(tài)時(shí)間緊迫度的逆序貪婪綜合調(diào)度算法
- 毫米波大規(guī)模MIMO系統(tǒng)波束旋轉(zhuǎn)預(yù)編碼設(shè)計(jì)

