哈默斯坦非線性時變系統的加權學習辨識方法

仲國民 俞其樂 陳 強

(浙江工業大學信息工程學院 杭州 310023)

1 引言

非線性特性廣泛存在于實際工業生產過程中，為便于研究其變化規律，需要用數學模型來對所研究的物理現象或過程進行定量分析，因此非線性系統辨識問題受到越來越多的關注。非線性系統結構復雜，難以采用統一模型進行描述，在過去的幾十年里，國內外學者主要致力于較普遍的塊結構非線性系統辨識[1]。塊結構非線性系統可以分為非線性靜態部分和線性動態部分，分別用非線性函數和線性函數來表示其特性[2]。其中，維納(Wiener)系統、哈默斯坦(Hammerstein)系統及其組合形式是應用最廣泛的配置。哈默斯坦系統廣泛應用于模擬連續攪拌釜式反應器、pH中和過程、蒸餾塔、液壓自動發電量控制系統、多傳感器系統等非線性過程或系統[3,4]。它由1個非線性靜態函數串聯和1個線性動態子系統構成，其中哈默斯坦受控自回歸滑動平均模型(Controlled AutoregRessive Moving Average model, CARMA)系統的具體形式描述如圖1所示。

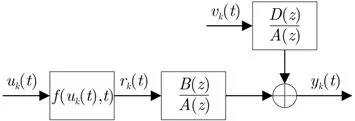
圖1 哈默斯坦系統CARMA模型

針對哈默斯坦系統的辨識問題，已開展較多研究工作，如子空間辨識法[5–8]、過參數化法[9,10]、最小二乘法[11]、極大似然法[12]、非參數核回歸估計[13,14]、分數階法[15]、基于特殊輸入信號的方法[16]和相關分析方法[17]等。文獻[16]提出一種識別哈默斯坦非線性過程的方法，該方法利用一個特殊的測試信號，能夠識別出哈默斯坦系統由1個非線性靜態函數和1個線性動態子系統組成。針對哈默斯坦非線性帶外部輸入的自回歸滑動平均模型(Autoreg-Ressive Moving Average model with eXogenous Input, ARMAX)，文獻[18]提出了一種迭代梯度算法。上述方法均是假設靜態非線性特性為子函數多項式的組合前提下，針對定常哈默斯坦系統開展的研究。現有帶遺忘因子遞推算法[19]、塊脈沖函數法[20]等能夠提高時變參數跟蹤性能；迭代學習辨識算法[21,22]有效解決了時變參數估計問題。鑒于塊結構時變非線性系統辨識方面的研究尚少，本文將迭代學習方法進一步運用于基于塊結構的非線性系統辨識。

本文提出一種加權迭代學習辨識的方法，其動機是已有系統辨識算法加權修正的思想[23]。當動態系統在有限區間上重復運行時，沿重復軸來看，固定時刻對應的參數是相對固定的，可以采用迭代學習算法估計時變參數。但由于實際中存在非重復初始條件和外部干擾，一致重復運行并不是總能保證的。因此，為提高參數估計精度和系統跟蹤效果，將時間軸上加權矩陣方法推廣運用于沿重復軸上的修正，構建加權迭代學習算法。

本文考慮有限區間上重復運行的哈默斯坦非線性時變系統，借助哈默斯坦定常系統辨識方法，采用輔助模型方法[24]，推導出哈默斯坦非線性時變系統基于“重復軸”的迭代學習最小二乘算法。同時，為避免數據飽和，引入遺忘因子，推導出帶遺忘因子迭代學習最小二乘算法。在此基礎上，進一步改進準則函數，引入權矩陣，探索一種加權迭代學習最小二乘(Weighted Iterative Learning Least Squares, WILLS)的辨識方法，并將該算法運用于時變哈默斯坦模型的辨識研究，其優點是達到一定辨識精度的條件下，迭代次數少，輸出誤差小且穩定性好。

2 問題描述

考慮如式(1)所述有限區間上重復運行的單輸入單輸出離散時變哈默斯坦系統

3 哈默斯坦非線性時變系統的加權學習辨識

3.1 迭代學習最小二乘算法

針對重復運行的哈默斯坦時變系統，考慮如式(19)的極小化準則函數

3.2 帶遺忘因子的迭代學習最小二乘算法

為避免數據飽和現象，增加新數據的權重，加快跟蹤誤差收斂速度及精度，在上述算法的基礎上引入遺忘因子λ，考慮如式(30)的準則函數

3.3 加權迭代學習最小二乘算法

上述兩類算法能獲得參數的一致估計，但對初始條件的一致性要求苛刻，且跟蹤精度有進一步提升的空間，下面提出一種加權的迭代學習算法以獲得更優跟蹤效果和辨識精度。為了得到參數θk(t)的估計，考慮如式(40)的準則函數[21]

4 數值算例

表1 采用加權迭代學習最小二乘算法進行參數估計流程圖

加權迭代學習算法的參數估計結果如圖2所示，3種算法的模型輸出誤差和參數估計誤差如圖3和圖4所示。仿真結果表明，加權迭代學習算法可以有效估計模型的時變參數。在迭代學習最小二乘算法的基礎上引入遺忘因子可以改善模型輸出誤差和參數估計誤差。考慮如式(40)的準則函數，引入加權矩陣，可以進一步降低模型輸出誤差，提高辨識精度，尤其在達到某一確定的參數估計誤差或模型輸出誤差時，迭代次數明顯減少，同時該算法可獲得更好的辨識效果。

圖2 采用加權迭代學習最小二乘算法的參數估計結果

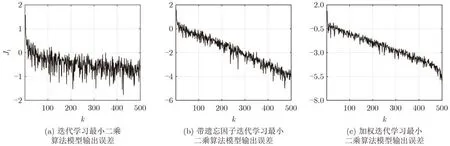
圖3 采用3種不同算法的模型輸出誤差比較

圖4 采用3種算法的參數估計誤差比較

5 結論

對于Harmmerstein非線性時變系統的參數估計問題，本文提出加權學習辨識算法，推導了重復運行條件下的迭代學習最小二乘法、帶遺忘因子迭代學習最小二乘法和加權迭代學習最小二乘法。在重復持續激勵條件下，仿真結果顯示加權學習辨識算法可以實現時變參數的完全估計。與現有辨識算法相比，本文算法進一步提高了時變參數的估計精度，提高了算法的跟蹤性能，在達到一定辨識精度下，加權算法可以減少重復運行的次數。