隱圓模型四種形式的探索解析

胡雅玲

【摘要】圓是重要的幾何圖形，其幾何性質應用廣泛，關于等角、等線段的特性結論在綜合性問題中有著重要應用.而有些題目在呈現時，并沒有明確設定圓，圓是隱性存在的，此時就需要根據圓的定義來提取或構建.通常隱圓模型有四種形式，下面結合問題具體探究.

【關鍵詞】隱圓模型;圓;數學解題

隱圓模型1 動點定長

動點定長模型，即動點到定點的距離為定長（定值）.該模型是基于圓幾何定義的衍生，即到定點的距離等于定長的點的集合稱之為圓，實際模型中體現在線段相等上，具體如下.

模型 如圖1所示，有AB=AC=AD，則B，C，D三點均在以A為圓心，AB為半徑的圓上.

策略 實際解題時需要證明出定長，常借用三角形全等或相似特性.

例1 如圖2所示，已知菱形ABCD中，其邊長為2，∠A=60°，點M為AD的中點，點N是AB邊長的一個動點，將△AMN沿著MN所在直線翻折可得到△A′MN，連接A′C，則A′C長度的最小值為.

解析 分析翻折過程，將△AMN沿著MN所在直線翻折得到△A′MN，由翻折特性可知始終有MA=MA′=1，與點N的位置無關.結合動點定長隱圓模型可知，點A′的軌跡為以點M為圓心，MA長為半徑的圓弧.

求A′C長度的最小值，連接CM，結合共線定理可知CM與圓的交點就為所求A′的位置，此時A′C長度最小，且A′C=MC-MA，其中MA=1，

過點M作CD的垂線，設垂足為點H，如圖3所示，∠MDH=60°，則CH=CD+DM·cos60°=52.在Rt△CHM中，利用勾股定理，可得MC=MH2+CH2=7，所以A′C=MC-MA=7-1，即A′C長度的最小值為7-1.

評析 上述線段最值問題中隱含了動點定長隱圓模型，解析的關鍵就是確定其中的定長，該定長與翻折特性密切相關，從而可直接確定動點的軌跡，后續結合三點共線可直接確定最值情形.

隱圓模型2 直角對直徑

直角對直徑隱圓模型，即90°角所對的線段為圓的直徑，該模型同樣是基于圓的特性定理所構建.根據該隱圓模型可知，任意直角三角形的直角頂點均在以斜邊長為直徑的圓上.實際上該模型屬于特殊的定弦定角模型.

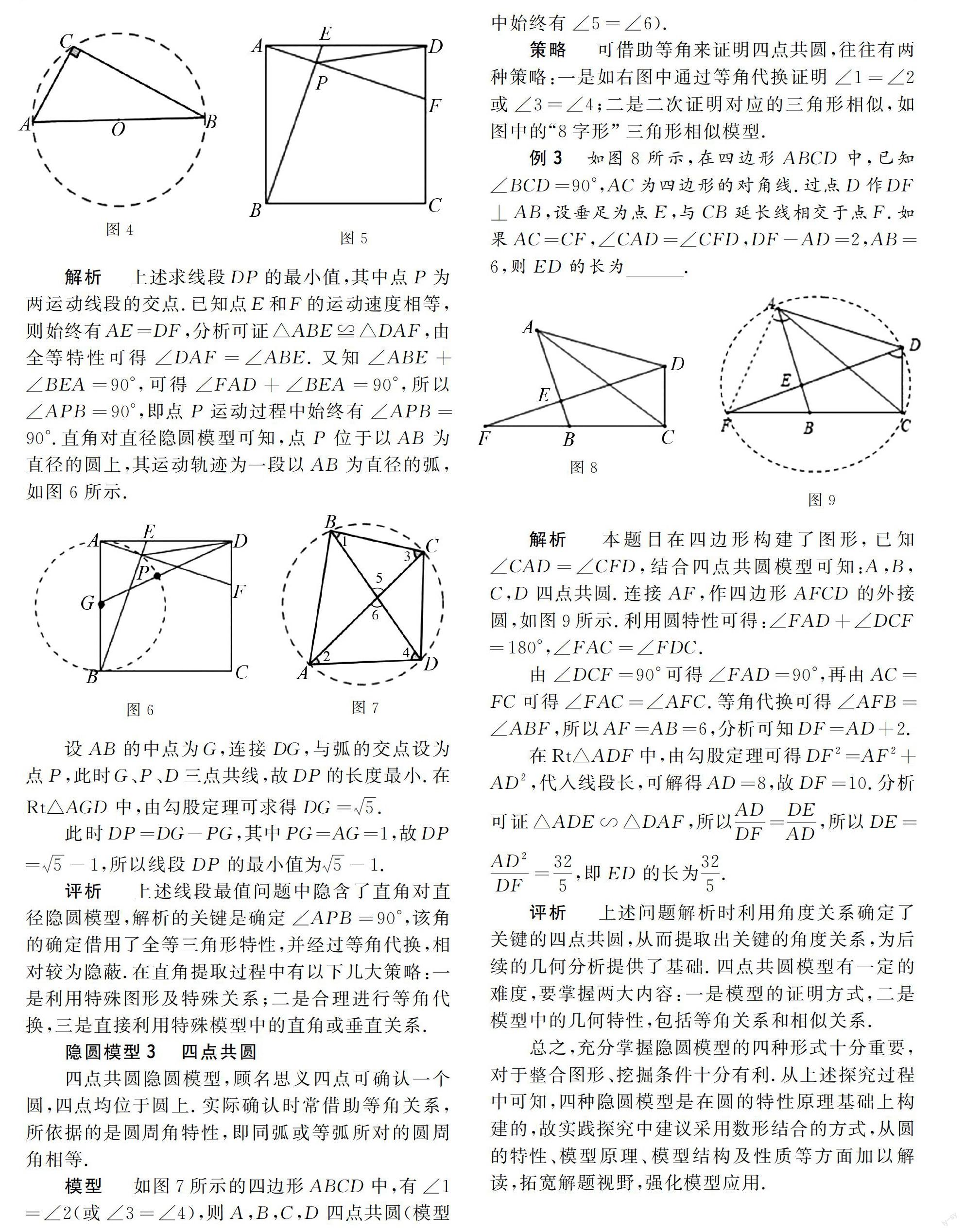
模型 如圖4所示，AB為固定線段，且總有∠ACB=90°，則點C位于以AB為直徑的圓上.

策略 該直角對直徑隱圓模型的確認核心為直角，故可直接提取圖形中的90°角，包括其中的特殊圖形，如矩形、正方形，特殊關系：垂直關系.解析時從特殊圖形、特殊關系入手來提取即可.

例2 如圖5所示，在正方形ABCD中，已知AB=2.動點E從點A出發，向點D運動;同時動點F從點D出發，向點C運動.點E和F的運動速度相等，當兩點到達各自的終點時停止運動.設運動過程中線段AF和BE的交點為P，則線段DP的最小值為.

解析 上述求線段DP的最小值，其中點P為兩運動線段的交點.已知點E和F的運動速度相等，則始終有AE=DF，分析可證△ABE≌△DAF，由全等特性可得∠DAF=∠ABE.又知∠ABE+∠BEA=90°，可得∠FAD+∠BEA=90°，所以∠APB=90°，即點P運動過程中始終有∠APB=90°.直角對直徑隱圓模型可知，點P位于以AB為直徑的圓上，其運動軌跡為一段以AB為直徑的弧，如圖6所示.

設AB的中點為G，連接DG，與弧的交點設為點P，此時G、P、D三點共線，故DP的長度最小.在Rt△AGD中，由勾股定理可求得DG=5.

此時DP=DG-PG，其中PG=AG=1，故DP=5-1，所以線段DP的最小值為5-1.

評析 上述線段最值問題中隱含了直角對直徑隱圓模型，解析的關鍵是確定∠APB=90°，該角的確定借用了全等三角形特性，并經過等角代換，相對較為隱蔽.在直角提取過程中有以下幾大策略：一是利用特殊圖形及特殊關系;二是合理進行等角代換，三是直接利用特殊模型中的直角或垂直關系.

隱圓模型3 四點共圓

四點共圓隱圓模型，顧名思義四點可確認一個圓，四點均位于圓上.實際確認時常借助等角關系，所依據的是圓周角特性，即同弧或等弧所對的圓周角相等.

模型如圖7所示的四邊形ABCD中，有∠1=∠2（或∠3=∠4），則A，B，C，D四點共圓（模型中始終有∠5=∠6）.

策略 可借助等角來證明四點共圓，往往有兩種策略：一是如右圖中通過等角代換證明∠1=∠2或∠3=∠4;二是二次證明對應的三角形相似，如圖中的“8字形”三角形相似模型.

例3 如圖8所示，在四邊形ABCD中，已知∠BCD=90°，AC為四邊形的對角線.過點D作DF⊥AB，設垂足為點E，與CB延長線相交于點F.如果AC=CF，∠CAD=∠CFD，DF-AD=2，AB=6，則ED的長為.

解析 本題目在四邊形構建了圖形，已知∠CAD=∠CFD，結合四點共圓模型可知：A，B，C，D四點共圓.連接AF，作四邊形AFCD的外接圓，如圖9所示.利用圓特性可得：∠FAD+∠DCF=180°，∠FAC=∠FDC.

由∠DCF=90°可得∠FAD=90°，再由AC=FC可得∠FAC=∠AFC.等角代換可得∠AFB=∠ABF，所以AF=AB=6，分析可知DF=AD+2.

在Rt△ADF中，由勾股定理可得DF2=AF2+AD2，代入線段長，可解得AD=8，故DF=10.分析可證△ADE∽△DAF，所以ADDF=DEAD，所以DE=AD2DF=325，即ED的長為325.

評析 上述問題解析時利用角度關系確定了關鍵的四點共圓，從而提取出關鍵的角度關系，為后續的幾何分析提供了基礎.四點共圓模型有一定的難度，要掌握兩大內容：一是模型的證明方式，二是模型中的幾何特性，包括等角關系和相似關系.

總之，充分掌握隱圓模型的四種形式十分重要，對于整合圖形、挖掘條件十分有利.從上述探究過程中可知，四種隱圓模型是在圓的特性原理基礎上構建的，故實踐探究中建議采用數形結合的方式，從圓的特性、模型原理、模型結構及性質等方面加以解讀，拓寬解題視野，強化模型應用.