從問題結構入手尋求解題方法

武前煒

【摘要】本文對4道有代表性的代數試題進行分析，抓住結構，尋求破題之策，特別對于一類9宮格數字問題給出一般性的性質.

【關鍵詞】 2022;數學結構;參數

數學的學習離不開問題的解決，好的數學問題能促進學生知識、技能、情感等各方面快速、健康的發展.伴隨著問題的解決能激發學生的學習興趣，驅使學生積極思考、主動參與學習、樂意尋求解決問題的答案.進入初中學習代數的過程，感受到了從數到式的直觀體驗，對于代數問題需要我們仔細觀察問題中數、數量、關系以及結構，通過抽象化的結構建立各種關系，以下通過幾個數學問題體會知識運用的靈活性、綜合性、創新性.

在一些有趣的數學問題中，時常見到題目中出現了當年的年份數，我們稱這樣的題為“年題”，隨著2022年的到來，為聰明的你準備了“2022”年份趣題，一起來開動腦筋吧！

例1 若x+y+z=6066（x>y>z，且都不等于2022），則分式

（x-2022）（y-2022）+（y-2022）（z-2022）+（z-2022）（x-2022）（x-2022）2+（y-2022）2+（z-2022）2的值等于.

分析 經觀察知條件和問題含有相似結構x-2022，y-2022，z-2022，考慮簡化運算，通過參數替換讓式子變得更簡單，便于發現熟悉的數學結構.

解 因為x+y+z=6066，

所以（x-2022）+（y-2022）+（z-2022）=0，

設x-2022=a，y-2022=b，z-2022=c，

即a+b+c=0，

所以（a+b+c）2=0，

即a2+b2+c2+2ab+2bc+2ca=0，

由x，y，z都不等于2022可知abc≠0，

原式=ab+bc+caa2+b2+c2=ab+bc+ca-2ab-2bc-2ca=-12.

例2 若2021（x-y）+2022（y-z）+2023（z-x）=0，20212（x-y）+20222（y-z）+20232（z-x）=2022，則z-y的值等于.

分析 題目條件的數字較大且未知數有相同對稱結構，考慮設參數替換，讓題目隱藏信息暴露出來.

解 設x-y=a，y-z=b，z-x=c，

則a+b+c=0，①

2021a+2022b+2023c=0，②

20212a+20222b+20232c=2022，③

①×2022得

2022a+2022b+2022c=0，④

④-②得a-c=0，

即a=c，⑤

③-②×2022，得

（20212a+20222b+20232c）-（2021×2022a+2022×2022b+2023×2022c）=2022，

即-2021a+2023c=2022，⑥

由①，⑤，⑥得

a=c=1011，b=-2022，

從而z-y=-b=2022.

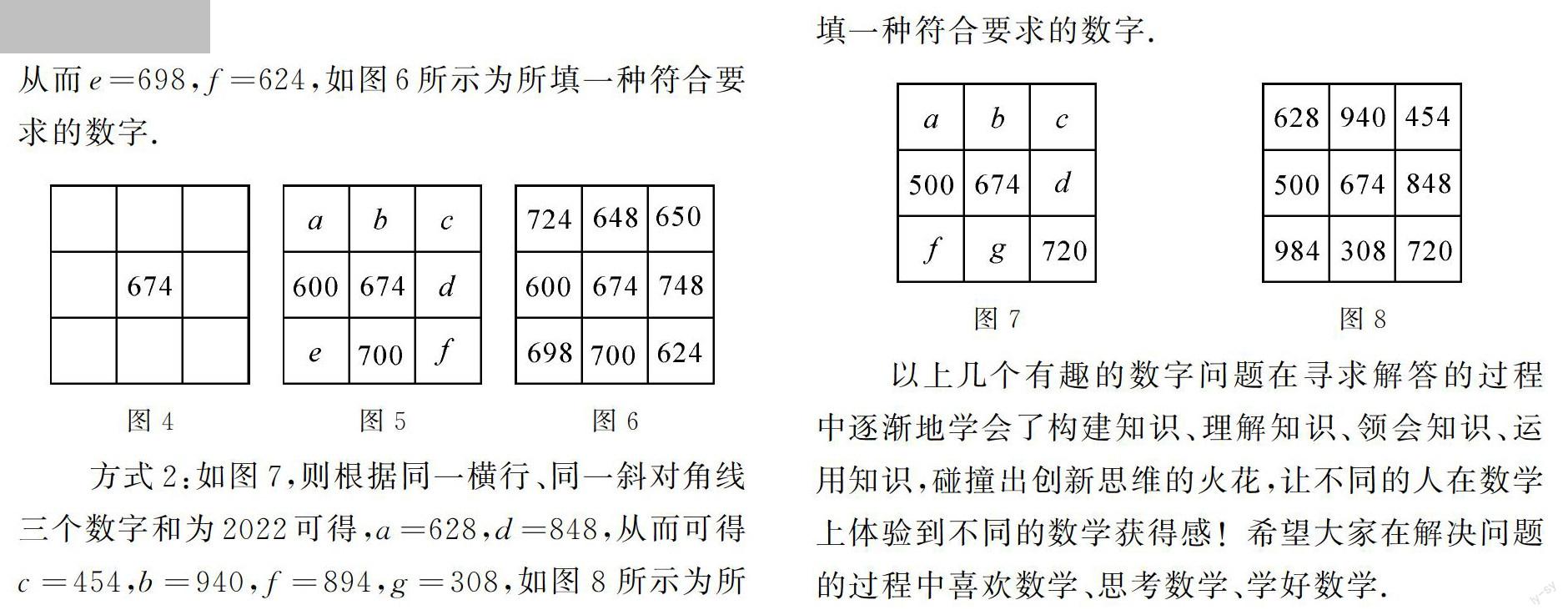
例3 對于每一個正整數m（0

解 由m2021

mn<2021x，mn+n>2022x，

則mn+1≤2021x，mn+n-1≥2022x，

2022（mn+1）≤2022×2021x，2021（mn+n-1）≥2021×2022x，

即2021（mn+n-1）≥2022（mn+1），

解得n≥40432021-m，

此式應對每一個正整數m（1

m2021

由不等式性質對于任意實數，若ab

ab

可知m2021

從而可得x=2m+1.

即當正整數n的最小值為4043，此時不等式組的正整數解是x=2m+1.

例4 將9個數填入九個方格中，使處于同一橫行、同一豎列、同一斜對角線上的三個數的和相等，如圖1：

請在如圖2中的九個方格格內填上合適的數，使處于同一橫行、同一豎列、同一斜對角線上的三個數的和都等于2022.

分析 本題屬于開放性數學問題，答案不唯一，那么如何快速準確填寫，需要研究此類九宮格數字隱藏的規律.

為方便研究，如圖3為填好的符合同一橫行、同一豎列、同一斜對角線上的三個數的和都等于M的九宮格.

則可知a+e+i=M，

c+e+g=M，

b+e+h=M，

d+e+f=M，

9個數字總和

a+b+c+d+e+f+g+h+i=3M，

即（a+e+i）+（b+e+h）+（c+e+g）+（d+e+f）-3e=3M，

所以e=13M，

從而可得a+i=23M，

變形得a-13M=13M-i，

即a-e=e-i，

從而可得對角線的三個方格數a，e，i為等差數列，

同理可得方格數c，e，g;b，e，h;d，e，f均為等差數列，

由（a+d+g）+（b+e+h）=（a+b+c）+（c+e+g）=2M，

整理可得（a+g+b+e）+（d+h）=（a+g+b+e）+2c，

即c=d+h2.

歸納 如圖3，若將9個數a，b，c，d，e，f，g，h，i填入九個方格中，且滿足處于同一橫行、同一豎列、同一斜對角線上的三個數的和相等，則這些方格數字具備以下性質：

性質1：所有數字和等于中間方格數字的9倍;

性質2：第2行，第2列以及兩個對角線中的三個數分別呈等差數列關系;

性質3：d+h=2c;h+f=2a;

f+b=2g;b+d=2i.

解 由題意知，要填的9個數和為

2022×3=6066，

由性質1知，中間方格數為

6066÷9=674，

如圖4，只需在剩下8個方格任填2個數（與中間674數字不構成對角線位置）即可確定其余數字，

方式1：如圖5，則根據同一橫行、同一豎列三個數字和為2022可得，

b=648，d=748，

再根據性質3可得

a=724，c=650，

從而e=698，f=624，如圖6所示為所填一種符合要求的數字.

方式2：如圖7，則根據同一橫行、同一斜對角線三個數字和為2022可得，a=628，d=848，從而可得c=454，b=940，f=894，g=308，如圖8所示為所填一種符合要求的數字.

以上幾個有趣的數字問題在尋求解答的過程中逐漸地學會了構建知識、理解知識、領會知識、運用知識，碰撞出創新思維的火花，讓不同的人在數學上體驗到不同的數學獲得感！希望大家在解決問題的過程中喜歡數學、思考數學、學好數學.