立體幾何中空間向量法的巧用

吳華紅

【摘要】立體幾何在歷年高考數學中占據了重要地位，每年必考題目.有些空間幾何問題用綜合法（即傳統的幾何法）去解決往往比較繁雜，而運用向量法作形與數的轉化，則能使過程得到大大的簡化，用向量法解決立體幾何問題有著思路清晰、過程簡潔的優點，往往會產生意想不到的效果.本文試圖通過對高考（或模擬）題解題方法和技巧的分析，使讀者領會空間向量解決立體幾何問題的神奇妙用.

【關鍵詞】向量;直線的方向向量;平面的法向量

1空間向量與空間點

例1在正三棱柱ABC＼|A1B1C1中，AB=AA1=1，點P滿足BP=λBC+μBB1，其中λ∈[0，1]，μ∈[0，1]，則（）

（A）當λ=1時，△AB1P的周長為定值.

（B）當μ=1時，三棱錐P＼|A1BC的體積為定值.

（C）當λ=12時，有且僅有一個點P，使得A1P⊥BP.

（D）當μ=12時，有且僅有一個點P，使得A1B⊥平面AB1P.（2021年新高考Ⅰ卷）

解易知，點P在矩形BCC1B1內部（含邊界）.

當λ=1時，

BP=BC+μBB1=BC+μCC1，

此時P∈線段CC1，△AB1P周長不是定值，

故（A）錯誤;

當μ=1時，

BP=λBC+BB1=BB1+λB1C1，

此時P點軌跡為線段B1C1，

而B1C1∥BC，即B1C1∥平面A1BC，

所以點P到平面A1BC的距離為定值，

故其體積為定值，即（B）正確;

當λ=12時，

BP=12BC+μBB1，

圖1

取BC，B1C1中點分別為Q，H，

則BP=BQ+μQH，

所以P點軌跡為線段QH，

不妨建立空間直角坐標系如圖1所示，則

A132，0，1，

P（0，0，μ），B0，12，0，

即A1P=-32，0，μ-1，

BP=0，-12，μ，

A1P·BP=μ（μ-1）=0，

所以μ=0或μ=1.

故H，Q均滿足，即（C）錯誤;

當μ=12時，

BP=λBC+12BB1，

取BB1，CC1中點分別為M，N，則

BP=BM+λMN，

所以P點軌跡為線段MN.

設P0，y0，12.

因為A32，0，0，

所以AP=-32，y0，12，

又A1B=-32，12，-1，

所以AP·A1B=34+12y0-12=0，

解得y0=-12，

此時P與N重合，即（D）正確.

綜上知，選（B）（D）.

2空間向量與空間位置關系

例2在四棱錐P＼|ABCD中，AB⊥AD，CD⊥AD，PA⊥底面ABCD，PA=AD=CD=2AB=2，M為PC的中點.

（1）求證：BM∥平面PAD;

圖2

（2）平面PAD內是否存在一點N，使MN⊥平面PBD？若存在，確定N的位置;若不存在，說明理由.

解以A為坐標原點，分別以AB，AD，AP為x軸，y軸，z軸建立空間直角坐標系，如圖2所示，則

B（1，0，0），D（0，2，0），

P（0，0，2），C（2，2，0），M（1，1，1）.

（1）因為BM=（0，1，1），

平面PAD的一個法向量為n=（1，0，0），

所以BM·n=0，即BM⊥n.

又BM平面PAD，

所以BM∥平面PAD.

（2）BD=（-1，2，0），PB=（1，0，-2）.

假設平面PAD內存在一點N，使

MN⊥平面PBD.

設N（0，y，z），則

MN=（-1，y-1，z-1），

從而MN⊥BD，MN⊥PB，

所以MN·BD=0，MN·PB=0，

即1+2（y-1）=0，-1-2（z-1）=0，

解得y=12，z=12，即N0，12，12，

所以在平面PAD內存在一點N0，12，12，

使MN⊥平面PBD.

3空間向量與空間距離

例3如圖3，已知四邊形ABCD，EADM和MDCF都是邊長為a的正方形，點P是ED的中點.

（1）求點D到直線BF的距離;

（2）求點P到平面EFB的距離.

圖3圖4

解如圖4，以D為坐標原點，分別以DA，DC，DM所在直線為x軸，y軸，z軸，建立空間直角坐標系，則

D（0，0，0），A（a，0，0），B（a，a，0），

C（0，a，0），M（0，0，a），E（a，0，a），F（0，a，a），

由中點坐標公式可得Pa2，0，a2.

（1）DB=（a，a，0），BF=（-a，0，a）.

DB在BF方向上的投影為

|DB·BF||BF|=|a×（-a）+a×0+0×a|（-a）2+02+a2

=22a，

故點D到直線BF的距離

d=|BD|2-|DB·BF||BF|2

=（a2+a2+02）-22a2

=62a.

（2）設n=（x，y，z）是平面EFB的單位法向量，則

|n|=1，n⊥平面EFB，

所以n⊥EF，n⊥BE.

又EF=（-a，a，0），EB=（0，a，-a），

所以x2+y2+z2=1，-ax+ay=0，ay-az=0.

解得y=z=33，

所以n=33，33，33，

又PE=a2，0，a2，

設所求距離為d1，則

d1=|PE·n|=33a.

圖5

4空間向量與空間角

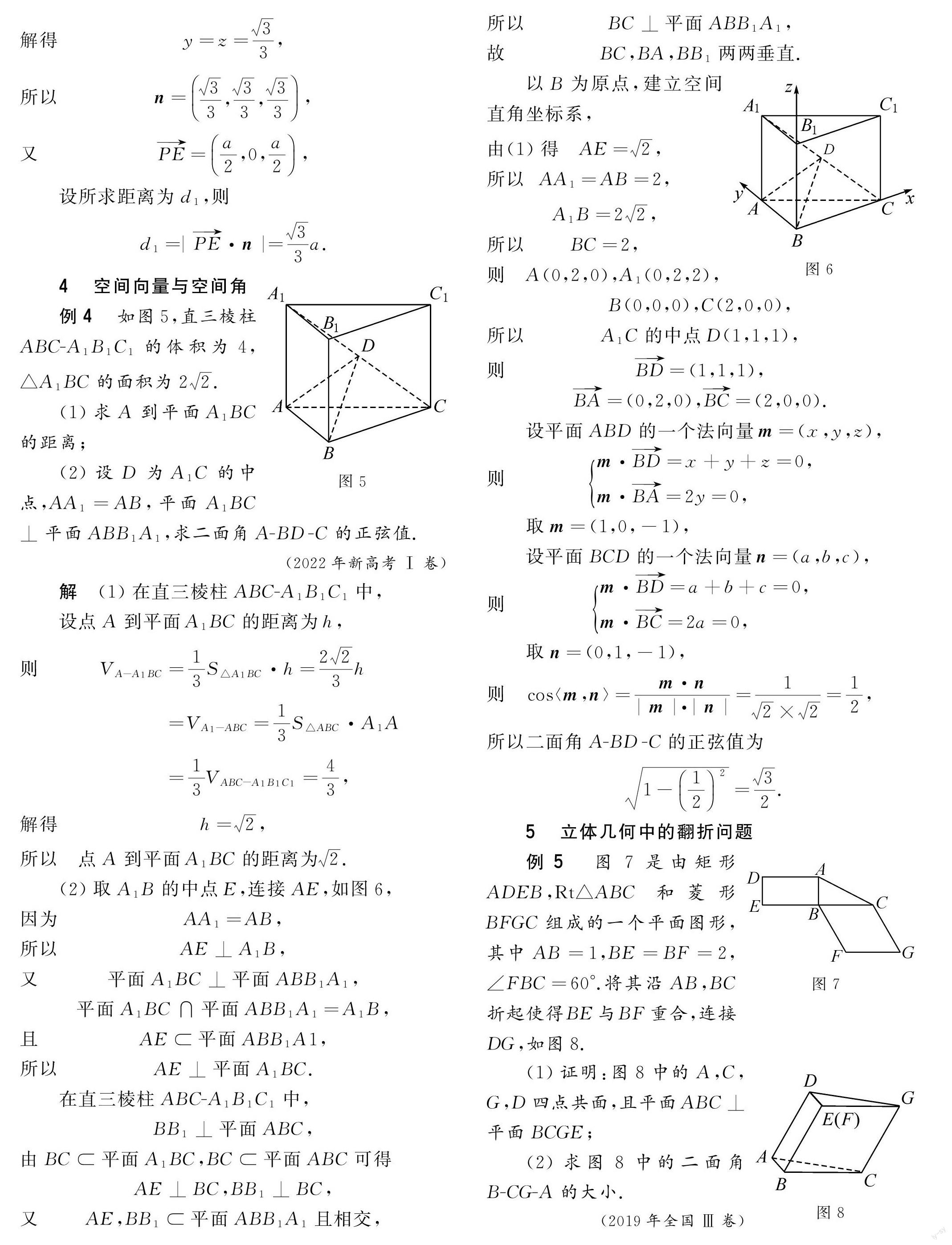
例4如圖5，直三棱柱ABC＼|A1B1C1的體積為4，△A1BC的面積為22.

（1）求A到平面A1BC的距離;

（2）設D為A1C的中點，AA1=AB，平面A1BC⊥平面ABB1A1，求二面角A＼|BD＼|C的正弦值.（2022年新高考Ⅰ卷）

解（1）在直三棱柱ABC＼|A1B1C1中，

設點A到平面A1BC的距離為h，

則VA-A1BC=13S△A1BC·h=223h

=VA1-ABC=13S△ABC·A1A

=13VABC-A1B1C1=43，

解得h=2，

所以點A到平面A1BC的距離為2.

（2）取A1B的中點E，連接AE，如圖6，

因為AA1=AB，

所以AE⊥A1B，

又平面A1BC⊥平面ABB1A1，

平面A1BC∩平面ABB1A1=A1B，

且AE平面ABB1A1，

所以AE⊥平面A1BC.

在直三棱柱ABC＼|A1B1C1中，

BB1⊥平面ABC，

由BC平面A1BC，BC平面ABC可得

AE⊥BC，BB1⊥BC，

又AE，BB1平面ABB1A1且相交，

所以BC⊥平面ABB1A1，

故BC，BA，BB1兩兩垂直.

圖6

以B為原點，建立空間直角坐標系，

由（1）得AE=2，

所以AA1=AB=2，

A1B=22，

所以BC=2，

則A（0，2，0），A1（0，2，2），

B（0，0，0），C（2，0，0），

所以A1C的中點D（1，1，1），

則BD=（1，1，1），

BA=（0，2，0），BC=（2，0，0）.

設平面ABD的一個法向量m=（x，y，z），

則m·BD=x+y+z=0，m·BA=2y=0，

取m=（1，0，-1），

設平面BCD的一個法向量n=（a，b，c），

則m·BD=a+b+c=0，m·BC=2a=0，

取n=（0，1，-1），

則cos〈m，n〉=m·n|m|·|n|=12×2=12，

所以二面角A＼|BD＼|C的正弦值為

1-122=32.

5立體幾何中的翻折問題

例5圖7圖7是由矩形ADEB，Rt△ABC和菱形BFGC組成的一個平面圖形，其中AB=1，BE=BF=2，∠FBC=60°.將其沿AB，BC折起使得BE與BF重合，連接DG，如圖8.

（1）證明：圖8中的A，C，G，D四點共面，圖8且平面ABC⊥平面BCGE;

（2）求圖8中的二面角B＼|CG＼|A的大小.（2019年全國Ⅲ卷）

解（1）由已知得AD∥BE，CG∥BE，

所以AD∥CG，

故AD，CG確定一個平面，

從而A，C，G，D四點共面.

由已知得AB⊥BE，AB⊥BC，

BE∩BC=B，

BE平面BCGE，BC平面BCGE，

所以AB⊥平面BCGE.

又AB平面ABC，

所以平面ABC⊥平面BCGE.

（2）如圖9，作EH⊥BC，垂足為H.

因為EH平面BCGE，

平面BCGE⊥平面ABC，

平面BCGE∩平面ABC=BC，

圖9

所以EH⊥平面ABC.

已知菱形BCGE的邊長為2，

∠EBC=60°，

可求得BH=1，EH=3.

以H為坐標原點，HC的方向為x軸的正方向，建立如圖9所示的空間直角坐標系H＼|xyz，則

A（-1，1，0），C（1，0，0），G（2，0，3），

CG=（1，0，3），AC=（2，-1，0）.

設平面ACGD的法向量為n=（x，y，z），

則CG·n=0，AC·n=0，即x+3z=0，2x-y=0.

所以可取n=（3，6，-3）.

又平面BCGE的法向量可取為m=（0，1，0），

所以cos〈n，m〉=n·m|n|·|m|=32，

因此二面角B＼|CG＼|A的大小為30°.

6立體幾何中的探索性問題

例6如圖10，在底面是菱形的四棱錐P＼|ABCD中，∠ABC=60°，PA=AC=a，PB=PD=2a，點E在PD上，且PE∶ED=2∶1.問：在棱PC上是否存在一點F，使BF∥平面AEC？證明你的結論.

解以A為原點，AD所在直線為y軸，AP所在直線為z軸，過A點且垂直于平面PAD的直線為x軸，建立空間直角坐標系，可知x軸垂直平分BC，

圖10圖11

B32a，-12a，0，C32a，12a，0，

P（0，0，a），E0，23a，13a.

設PF=λPC（0≤λ≤1），

則F32λa，12λa，（1-λ）a，

所以BF=32a（λ-1），12a（λ+1），（1-λ）a.

設n=（x，y，z）為平面AEC的法向量，

則n⊥AE=0，n⊥AC=0，

即（x，y，z）·0，23a，13a=0，（x，y，z）·32a，12a，0=0，

所以z=-2y，x=-33y.

令y=-1，得n=33，-1，2.

若BF∥平面AEC，

則BF⊥n，即BF·n=0，

所以32a（λ-1），12a（λ+1），（1-λ）a·

33，-1，2=0，

解得λ=12，此時F為PC的中點.

因此，在棱PC上存在一點F34a，a4，a2，

使BF∥平面AEC.