金剛石圓鋸片行波共振分析及優化

趙 雷，張德臣，閆春寶，雷忠興，程黎斌

（遼寧科技大學 機械工程與自動化學院,遼寧 鞍山 114051）

圓鋸片因其加工效率高且質量好而被廣泛應用，是工業切割中最常用的工具。但在切割加工中產生的噪聲污染是不容忽視的，高頻噪聲對環境、作業者的健康等造成一定程度的危害。圓鋸片切割時產生噪聲的源頭是由于鋸片的振動，需對其進行減振處理，才能有效降低或減少其噪聲的產生[1]。

近年來，對圓鋸片振動問題的研究相當活躍。范勇等[2]對圓鋸片的結構和模態振型進行了研究。FENG 等[3]研究了不同開槽長度圓鋸片的振動特性以及槽的參數變化對振動模態的影響。田永軍等[4]通過建立優化參數后的數學模型，分析了圓鋸片的聲學和應力影響規律。于家偉[5]利用有限元法（finite element method，FEM）和邊界元法（boundary element method，BEM）結合的方法，對不同孔型圓鋸片的噪聲進行了探究。早坂謙司等[6-7]對直徑為600 mm 的金剛石圓鋸片進行了大量試驗研究，發現40 個齒的圓鋸片在工作轉速為1 998 r/min 時，會在2 600 Hz 出現114 dB的高頻噪聲。上述關于圓鋸片降噪的研究，多側重于圓鋸片試驗及其振動振型的分析，沒有結合具體的行波振動理論來進一步分析其噪聲問題。

因此，在早坂謙司等[6-7]試驗的基礎上，對1 998 r/min空轉的?600 mm 金剛石圓鋸片進行行波共振理論分析。首先，通過Workbench 軟件對不同開孔方案的圓鋸片行波進行分析，在此基礎上對圓鋸片進行夾層處理；再次，運用行波振動理論分析其減振降噪特性；最后，靜力分析其是否滿足剛度需求，以檢驗優化方案的可行性。

1 金剛石圓鋸片模型建立

1.1 有限元模型基本參數

以?600 mm 的金剛石圓鋸片為研究對象，其基本結構模型見圖1，基本參數如表1所示。

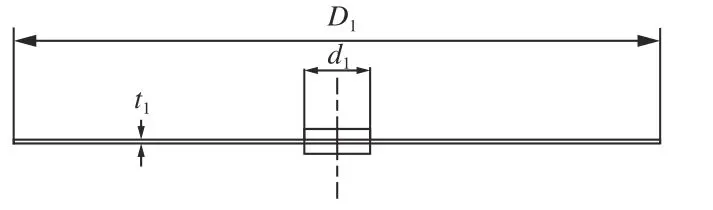
圖1 金剛石圓鋸片結構模型Fig.1 Structural model of diamond circular saw blade

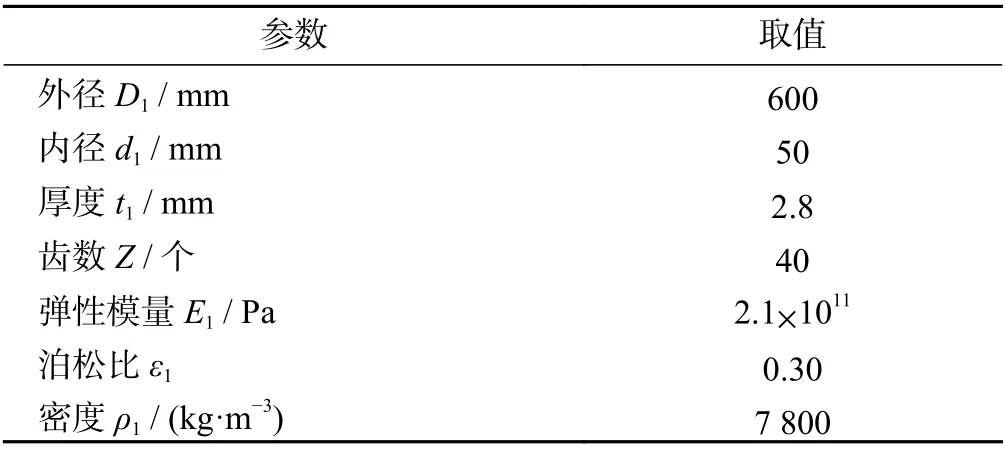
表1 ?600 mm 金剛石圓鋸片基本參數Tab.1 Basic parameters of ?600 mm diamond circular saw blade

1.2 模型網格劃分

在進行模擬仿真前，需對圓鋸片進行網格劃分，網格劃分的質量關系到求解模型的精度。圓鋸片網格劃分時著重對其鋸齒和內徑的網格進行細化，提高其相關度直至最大，并通過Refinement 網格命令對圓鋸片的其他局部及網格質量差的地方再進行細化。圓鋸片劃分的網格大小為5 mm，其網格劃分結果如圖2所示。金剛石圓鋸片網格劃分時，需對其法蘭盤內徑進行約束，由于鋸片發生共振時的頻率都在2 000 Hz 以上[6-7]，所以取的計算模態階數為200 階。

圖2 金剛石圓鋸片網格劃分圖Fig.2 Grid division diagram of diamond circular saw blade

2 金剛石鋸片行波振動分析

當圓鋸片的激振頻率與前行波頻率（或后行波頻率）接近時，就會產生行波共振現象，進而產生高頻噪聲。行波共振會損壞圓鋸片的性能，加快其損耗，縮短其使用壽命。為了避免高頻噪聲產生，可以在圓鋸片基體上開孔，進而降低圓鋸片的振動和噪聲。

2.1 金剛石圓鋸片基體開孔方案設計

將?600 mm 基體未開孔的圓鋸片作為方案一。在此基礎上另設2 種改進的開孔方案，所開的孔均為流線形孔，但具體的孔形狀在各方案中有所不同，目的就是為了打破圓鋸片的對稱性，破壞其振動模態，有效控制噪聲。方案二是同尺寸圓鋸片基體上開140 個圓形流線緯向孔，方案三是同樣基體上開48 個雨滴形流線緯向孔。圓鋸片基體開孔的3 種方案如圖3所示。

圓鋸片開孔后的處理程序如下：

（1）根據圖3的3 種開孔方案，計算金剛石圓鋸片模態階數為200 階時的固有頻率。由于其固有頻率數據繁多，取整理的部分典型數據列于表2中。

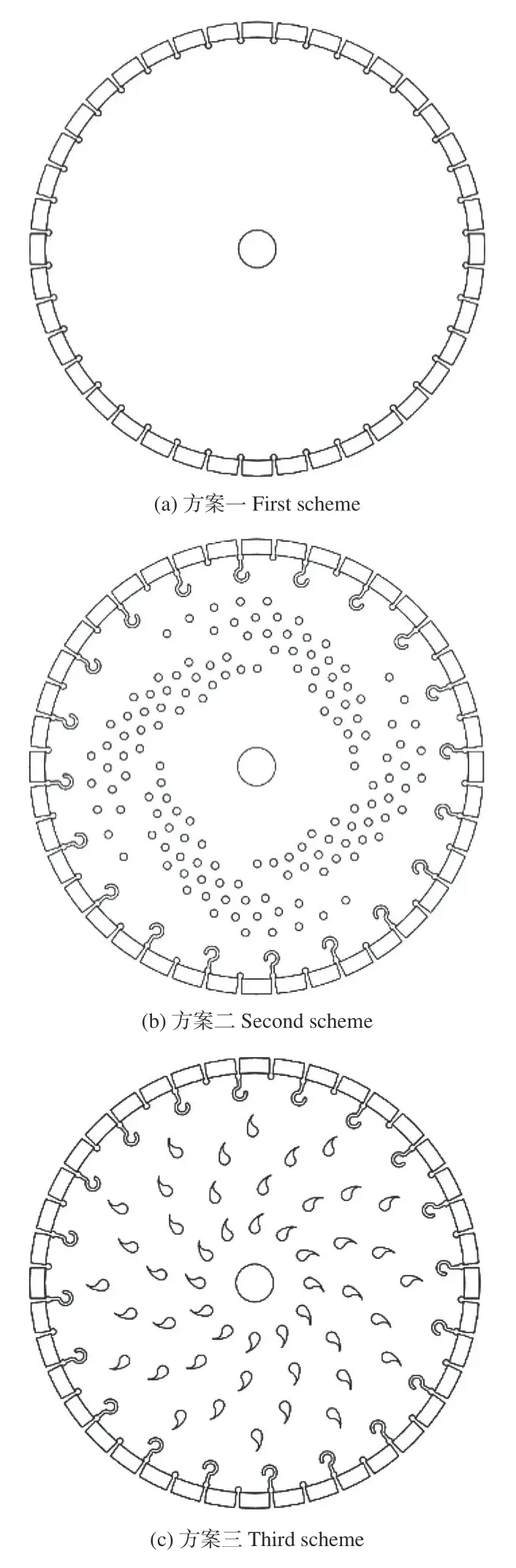
圖3 基體不同開孔方案的金剛石圓鋸片模型圖Fig.3 Model diagram of diamond circular saw blade with different opening schemes of matrix

由表2可明顯看出：與方案一比較，改進后的方案二和方案三的固有頻率降低。進一步分析可發現，前10 階的固有頻率降低不明顯，10～90 階的固有頻率降低，90 階之后的則顯著降低。說明開孔對低階頻率產生的影響不顯著，對高階頻率產生的影響顯著，且會使固有頻率顯著減小。

（2）根據表2中的數據，找出各個方案的典型模態圖，結果如圖4所示。其中，圖4a 是方案一中圓鋸片的1 個節圓12 個節直徑模態圖，圖4b 是方案二中圓鋸片的5 個節圓1 個節直徑模態圖，圖4c 是方案三中圓鋸片的4 個節圓5 個節直徑模態圖。

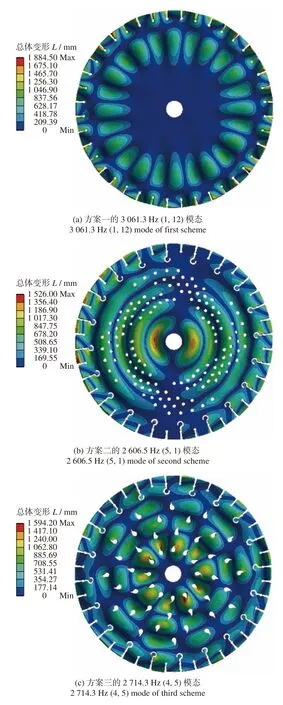
圖4 3 種方案的典型模態圖Fig.4 Typical modal diagrams of three methods

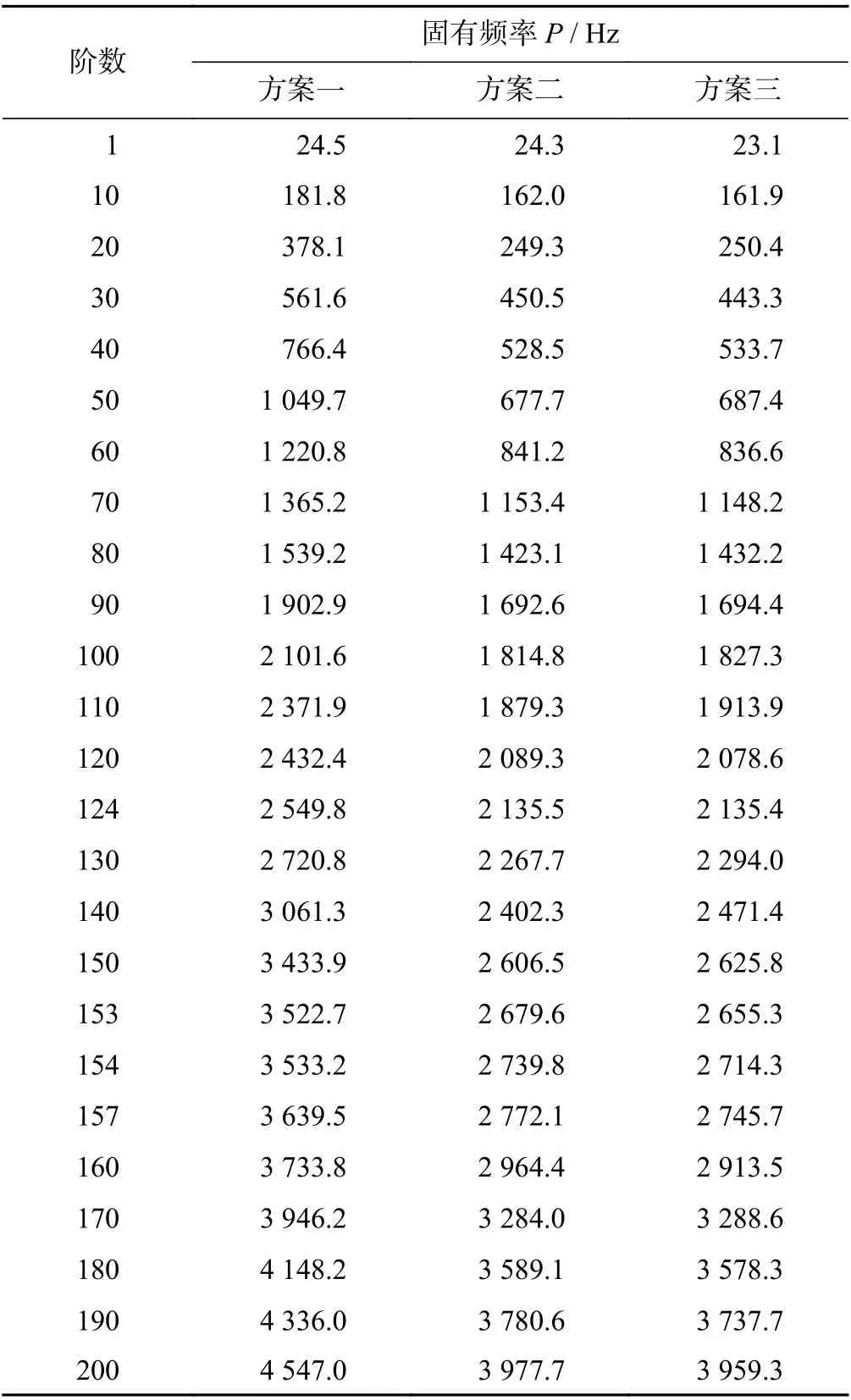
表2 ?600 mm 基體開孔金剛石圓鋸片固有頻率表Tab.2 Natural frequency table of ?600 mm matrix slotted diamond circular saw blade

2.2 行波振動分析

根據行波振動理論得到圓鋸片的行波頻率公式：

其中：Pf代表圓鋸片前行波振動頻率；Pb代表圓鋸片后行波振動頻率；P(m,n)代表圓鋸片的固有頻率；m表示圓鋸片模態圖中的節圓數，n表示圓鋸片模態圖中的節直徑數；Ω代表圓鋸片的轉速。

鋸齒通過頻率就是激振頻率，其為：

其中：p、Z分別為鋸片的鋸齒通過頻率和齒數；K為自然數，這里K取2。

行波振動頻率與鋸齒通過頻率差值的最小值Δ與鋸齒通過頻率p的比值δ為：

可通過δ值的大小來判定和比較圓鋸片及其各設計方案產生行波共振的程度，δ值越大，減振效果越明顯，越不容易發生行波共振。

由表2結果計算整理得到圓鋸片行波振動分析數據表3和δ值分布圖5。

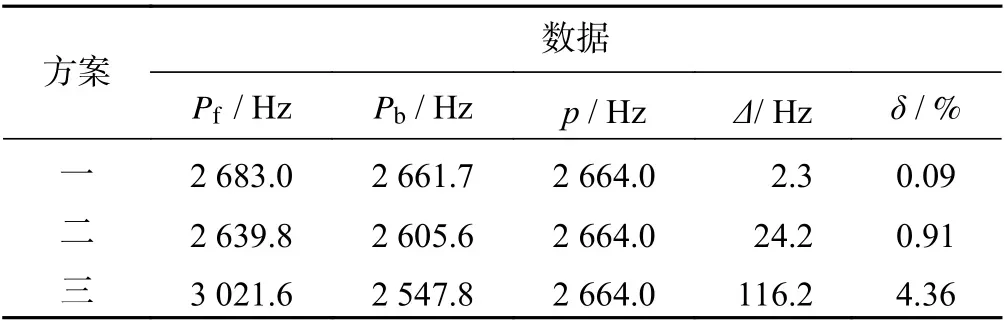
表3 金剛石圓鋸片的行波振動分析數據表Tab.3 Data sheet of traveling wave vibration analysis of diamond circular saw blade

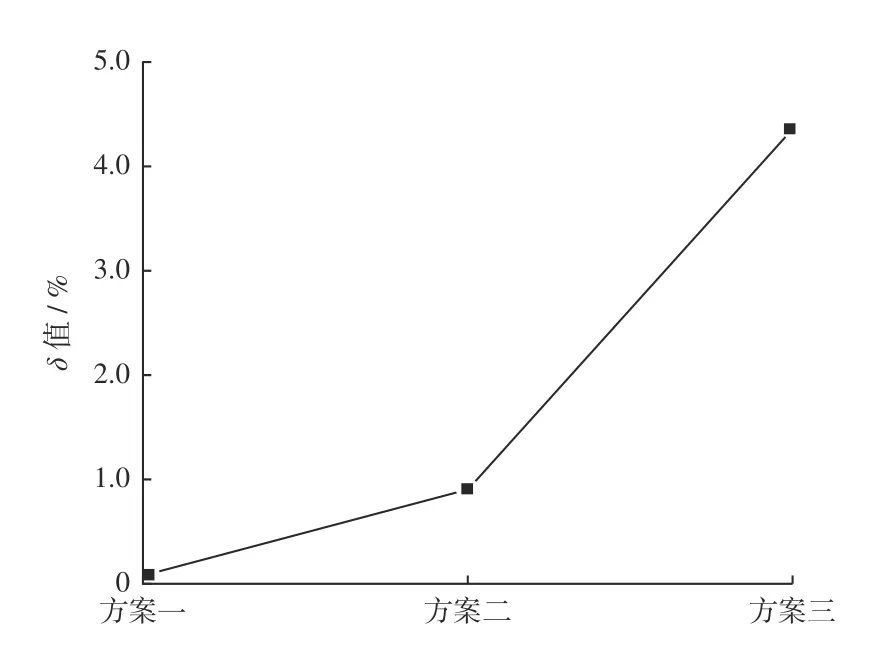
圖5 δ 值分布圖Fig.5 δ value distribution diagram

由表3、圖4和圖5可知：方案一的金剛石圓鋸片振動模態為1 個節圓12 個節直徑模態，此時金剛石圓鋸片的Δ、δ值分別為2.3 Hz 和0.09%，說明其會出現2 661.7 Hz 的后行波共振而產生嘯叫噪聲，這與文獻[6-7]中1 998 r/min 下的40 齒的空轉圓鋸片，在2 600 Hz的后行波共振時出現114 dB 的高頻噪聲試驗結果基本吻合。

由表3、圖4和圖5還可知：方案二、方案三的振動模態分別為5 個節圓1 個節直徑和4 個節圓5 個節直徑，其δ值分別為0.91% 和4.36%，均遠大于方案一的δ值0.09 %，說明其可以避開行波共振，遠離高頻噪聲。同時，對比3 個方案的結果發現，方案三的δ值最大，減振效果最理想，相比方案一和方案二更不易發生行波共振，是所有方案中最優的方案。

3 方案的進一步優化設計

在圓鋸片基體上開孔能夠較好地減小行波共振和噪聲，也是最為經濟的一種方法，但在實際應用中往往會在開孔的基礎上再進行夾層處理，夾層處理后的圓鋸片所達到的減振降噪效果更好[8]。因此，選取設計方案中最優的方案三進行進一步的處理。

在金剛石圓鋸片方案三的基礎上，在其內部添加阻尼夾層，阻尼夾層的開孔方案與圓鋸片一致，使其完全貼合方案三，命名為方案四。方案四的模型如圖6所示，阻尼夾層基本參數如表4所示。

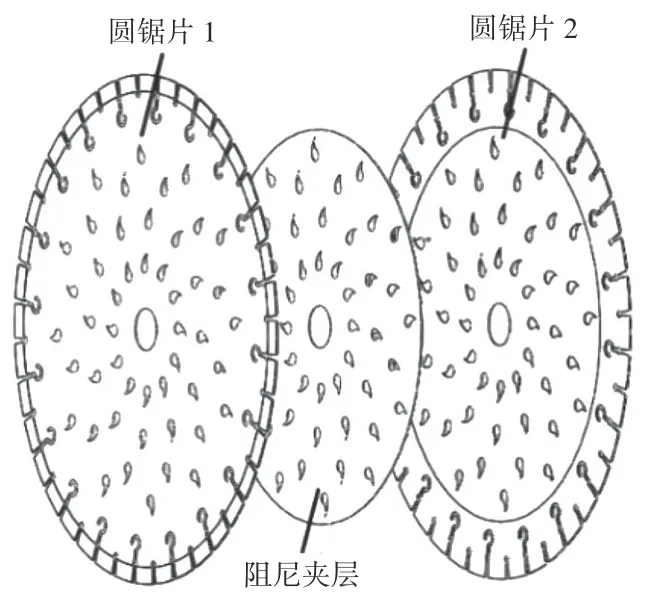
圖6 方案四中基體有開孔夾層的金剛石圓鋸片Fig.6 Diamond circular saw blade with matrix slotted interlayer in forth scheme

表4 阻尼夾層基本參數Tab.4 Basic parameters of damping interlayer

對方案四進行模擬分析，發現其150 階后的模態圖形狀變得極不規則，找不到完整的節圓及節直徑，因此取前150 階的固有頻率進行計算，結果如表5所示。再將方案四的結果與方案三的結果比較，得到圖7的對比圖。為簡略，圖7中只畫出階數分別為10,20,···,150 時的對應頻率值。

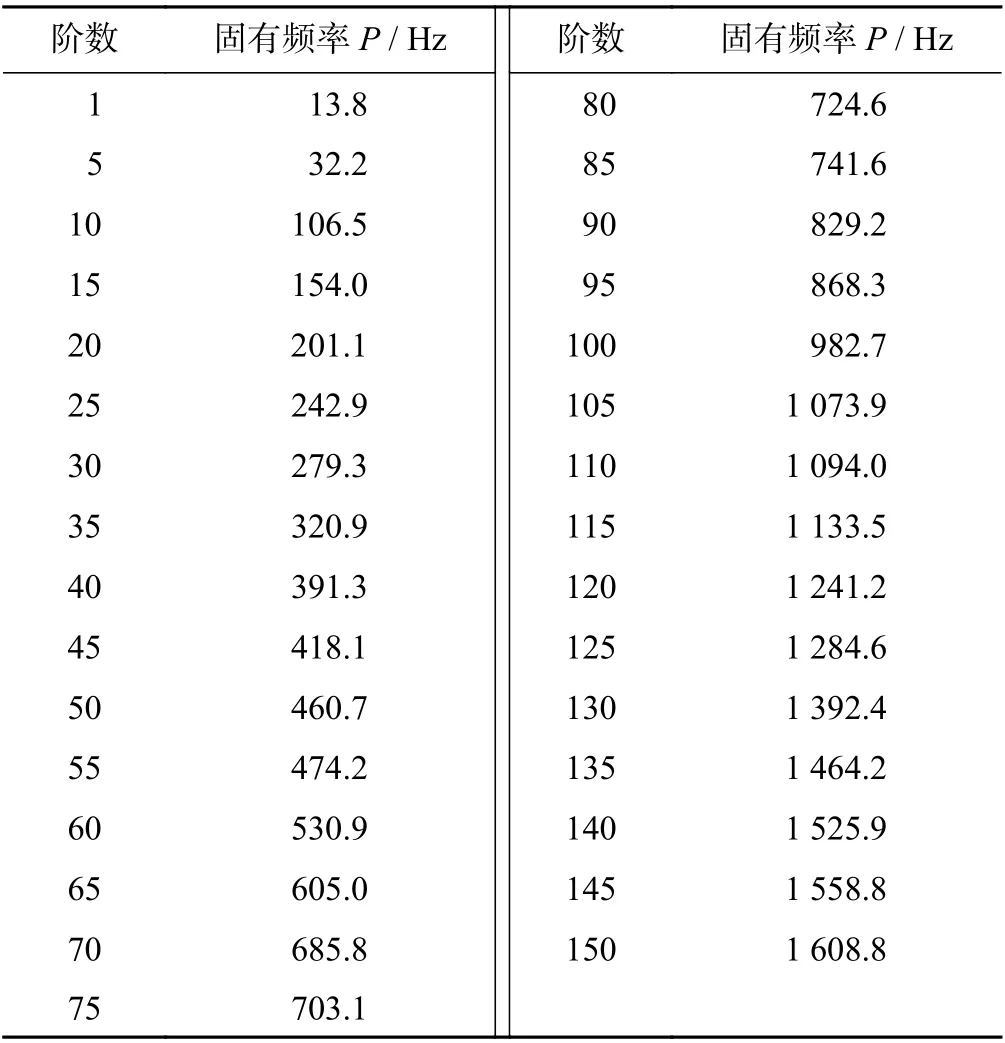
表5 方案四中100 階的固有頻率Tab.5 100 order natural frequencies in method 4

從圖7中可發現：有夾層的金剛石圓鋸片的固有頻率明顯降低。從20 階開始，方案四比方案三的固有頻率大幅下降；在100 階的時候，其固有頻率減小了900 Hz 左右，說明有開孔夾層的金剛石圓鋸片對其模態影響較大。

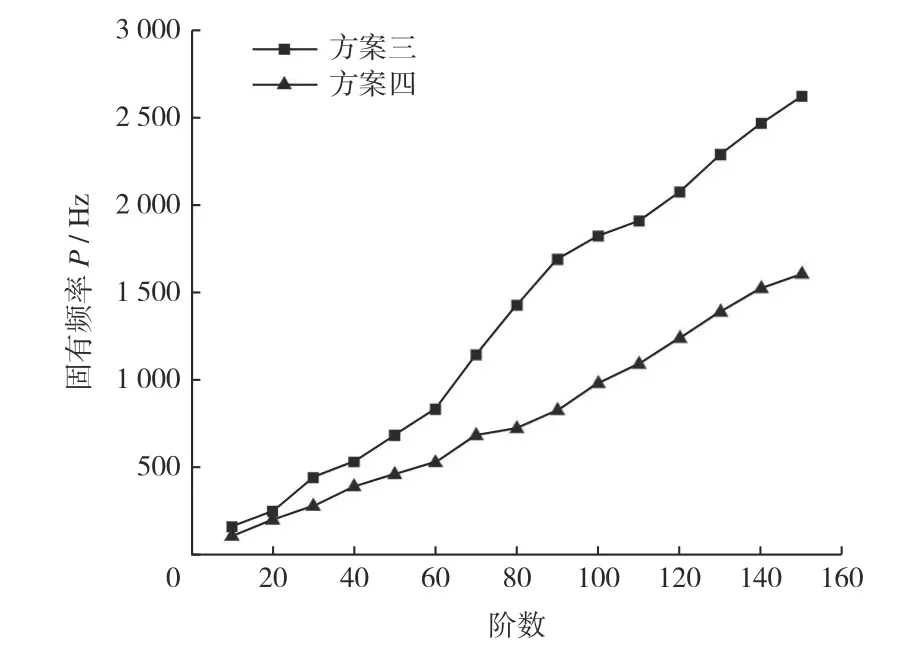
圖7 方案對比圖Fig.7 Scheme comparison chart

圖8為方案四的典型模態圖，其有4 個節圓7 個節直徑。式（3）中的K取1，得方案四的激振頻率為1 332.0 Hz，其行波振動分析數據如表6所示。 由圖8和表6所得數據可知：方案四的振動模態的δ值達到7.58%，相較于方案三的未進行夾層處理的圓鋸片，其δ值增大了近2 倍。說明有開孔夾層的金剛石圓鋸片對行波共振的抑制效果顯著，可以進一步避免行波共振，達到減少噪聲的目的。

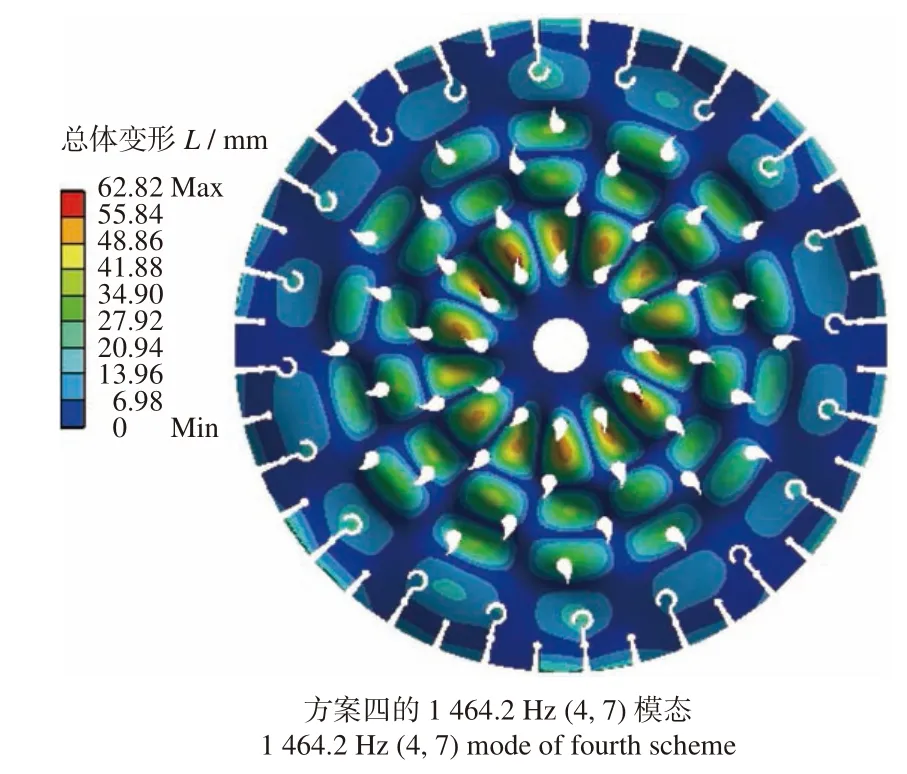
圖8 方案四的典型模態圖Fig.8 Typical modal diagram of fourth scheme

表6 方案四的行波振動分析數據Tab.6 Traveling wave vibration analysis data of fourth scheme

4 靜力分析

上面設計的開孔及夾層方案只考慮了圓鋸片的減振降噪效果，沒有考慮圓鋸片開孔及夾層后的受力變形問題和剛度問題[9-10]。圓鋸片在加工時反復與工件摩擦，時間久了很容易產生變形和疲勞裂紋，且變形和裂紋會隨著時間的推移不斷擴展，最終發生疲勞斷裂，導致圓鋸片無法工作。因此，有必要對開孔及夾層后的圓鋸片進行靜力有限元仿真。

圓鋸片基體材料采用65 Mn 鋼，根據圓鋸片的工作狀態，其切削深度選擇20 mm。據房懷英等[11]的分析，圓鋸片靜力分析時加載的軸向力取60 N。將內徑作為約束，轉速仍為1 998 r/min，并取方案一和方案四的數據進行比較。圖9為2 種方案下金剛石圓鋸片靜力分析的總體變形和應力分布圖。

如圖9所示：方案一中圓鋸片總的變形最大值為7.99×10-3mm，發生變形的位置主要在鋸齒上；最大的應力值為22.89 MPa，發生最大應力的位置在法蘭盤附近，說明圓鋸片發生破裂的位置會出現在法蘭盤附近。方案四中總的變形最大值為1.88×10-2mm，發生變形的位置集中在鋸齒及其附近，相比于方案一時的變形區域變大，最大變形值也變大；最大應力值為56.99 MPa，相比于方案一時的也變大了，且應力最大位置發生在法蘭盤及其開孔附近。

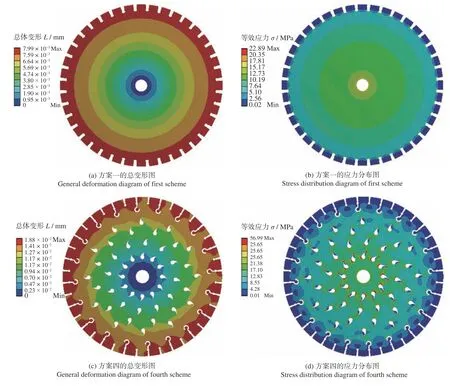
圖9 金剛石圓鋸片總體變形和應力分布圖Fig.9 Overall deformation and stress distribution of diamond circular saw blade

因此，從最大變形值和應力值來看，優化后的方案可以避開行波共振，但其變形值和所受應力值變大了；另一方面，65 Mn 鋼的抗拉強度為980.00 MPa，屈服強度為785.00 MPa，故改進后的圓鋸片應力值遠小于65 Mn鋼的強度值。說明優化后的圓鋸片雖然應力和變形增大，但其應力遠不能造成圓鋸片的失效斷裂，所設計的開孔及夾層圓鋸片方案是合理的，可以在實現規避行波共振的同時滿足其工作時的強度和剛度要求。

5 結論

對空轉的?600 mm 金剛石圓鋸片的3 個開孔方案（不開孔的方案一、開140 個圓形流線緯向孔的方案二及開48 個雨滴形流線緯向孔的方案三），通過Workbench 軟件對其進行行波理論分析，在此基礎上對圓鋸片進行夾層處理，分析其減振降噪特性，并靜力分析其最大變形及最大應力是否滿足基體本身的強度及剛度需求。得出如下結論：

（1）開孔金剛石圓鋸片可以打破未開孔圓鋸片的原模態規律，有效規避行波共振，降低工作時的噪聲。其中，方案三的δ值為4.36%，遠大于其他2 種方案的0.09%和0.91%，其減振效果最佳。

（2）對方案三的開孔金剛石圓鋸片進一步處理，即在開孔的基礎上再在其內部添加阻尼夾層，其δ值達到7.58%，相較其夾層前的值增大近1 倍，表明夾層處理后的圓鋸片能進一步規避行波振動，明顯抑制噪聲產生。

（3）金剛石圓鋸片的靜力分析結果表明，開孔及夾層處理后的圓鋸片的變形值和應力值相較未處理時的有所變大，但其應力值遠小于鋸片基體本身許用的強度值，不會對圓鋸片的疲勞壽命造成明顯影響，可在實現降低行波共振的同時滿足其工作時的強度及剛度需求。