借助圖形之變化，彰顯“抽象”之本質(zhì)
——以直線和圓的位置關(guān)系教學(xué)為例

吳建惠 周敏剛 劉盼盼 李 碩*

（1.昌吉學(xué)院數(shù)學(xué)與數(shù)據(jù)科學(xué)學(xué)院 新疆 昌吉 831100；2.昌吉市教育局 新疆 昌吉 831100）

近年來，隨著新一輪課程改革的不斷推進(jìn)，新的思潮和教育理念不斷涌現(xiàn)，其中影響范圍最廣的就是核心素養(yǎng)。各學(xué)科都有不同的學(xué)科核心素養(yǎng)，各學(xué)科核心素養(yǎng)之間既互相區(qū)別又密切聯(lián)系，共同為發(fā)展學(xué)生核心素養(yǎng)服務(wù)。《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)》（2017年版）（以下簡稱《課標(biāo)》）凝練出了數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、數(shù)學(xué)運算、直觀想象、數(shù)據(jù)分析六個方面的學(xué)科核心素養(yǎng)。

數(shù)學(xué)抽象作為六大學(xué)科核心素養(yǎng)之首，是數(shù)學(xué)發(fā)展所依賴的核心思想，是數(shù)學(xué)活動最基本的思維方式，它是從數(shù)量和數(shù)量關(guān)系、圖形和圖形的關(guān)系中抽象出數(shù)學(xué)概念和形成理性思維的重要基礎(chǔ)。［1］數(shù)學(xué)在本質(zhì)上研究的是抽象的東西，因此可以推斷，數(shù)學(xué)的發(fā)展所依賴的最重要的基本思想也就是抽象，因為只有通過抽象才能得到抽象的東西。［2］對于基礎(chǔ)教育的一線教師來說，教學(xué)中往往比較關(guān)注知識技能的掌握，對學(xué)生抽象思維的發(fā)展過程關(guān)注不夠，這也導(dǎo)致了低效學(xué)習(xí)現(xiàn)象頻發(fā)。那么，怎樣的數(shù)學(xué)活動既能承載知識，又能凸顯思維發(fā)展？這是新課改對教師提出的挑戰(zhàn)，要求廣大教師發(fā)揮教學(xué)智慧，創(chuàng)新教學(xué)活動，在活動中呈現(xiàn)問題與思考、促進(jìn)思維與發(fā)展。下面就以人教版九年級上冊24.2.2直線和圓的位置關(guān)系為例來探討運用圖形的變化凸顯數(shù)學(xué)抽象本質(zhì)的學(xué)習(xí)。

1 備課思考

1.1 教材分析

直線和圓的位置關(guān)系是點和圓的位置關(guān)系的后續(xù)課，從知識結(jié)構(gòu)上來看，直線和圓的位置關(guān)系是今后學(xué)習(xí)圓的切線的重要基礎(chǔ)，在本章中起著承上啟下的作用。從教法學(xué)法上來看，學(xué)生在學(xué)習(xí)了點與圓的位置關(guān)系后，基本掌握通過幾何量的大小關(guān)系判斷幾何圖形的位置關(guān)系，為本節(jié)課的研究提供了直觀的感知和鋪墊。由于本章開始研究圓形，要從學(xué)生熟悉的直線型過度到曲線型，學(xué)生在解決問題的方法上還缺乏經(jīng)驗，怎樣化曲為直，怎樣抓住曲線圖形的關(guān)鍵要素是本節(jié)課要重點突破的地方。

要解決上述問題，需要創(chuàng)設(shè)適當(dāng)?shù)臄?shù)學(xué)情境、提煉關(guān)鍵要素、建構(gòu)合理的數(shù)學(xué)活動平臺，于是形成如圖1所示的教學(xué)框架。

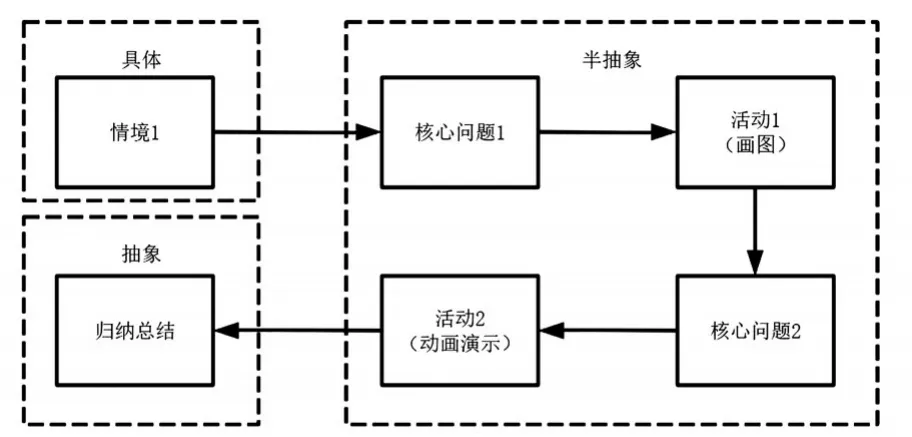
圖1 教學(xué)框架

1.2 學(xué)情分析

學(xué)生經(jīng)過了學(xué)習(xí)點與圓的位置關(guān)系，積累了初步的學(xué)習(xí)經(jīng)驗，也有了研究這一類問題的一些直觀的感受，但對研究曲線圖形還有一定的陌生感，學(xué)生很容易從直觀圖形上發(fā)現(xiàn)直線與圓的三種位置關(guān)系，但對這三種位置關(guān)系不能使用數(shù)學(xué)語言進(jìn)行定量的刻畫。教學(xué)是師生的雙邊活動，從教師備課的準(zhǔn)備上來看，多數(shù)教師認(rèn)為本節(jié)課比較簡單，由看圖很容易得出三種分類，進(jìn)而講解三種分類的兩種判定方法，忽視了學(xué)生通過探究活動，抽象出幾何要素及要素間關(guān)系的過程，只重視結(jié)果及結(jié)果的運用。

1.3 目標(biāo)分析

基于以上學(xué)情制定如下教學(xué)目標(biāo)。

目標(biāo)1：通過畫圖，歸納出定性判斷直線與圓的位置關(guān)系的方法。

目標(biāo)2：通過動畫探究，抽象出幾何要素并能夠定量表示三種位置關(guān)系，滲透分類討論、數(shù)形結(jié)合的數(shù)學(xué)思想。

目標(biāo)3：能利用d與r的大小關(guān)系判斷具體情境中的直線與圓的位置關(guān)系，培養(yǎng)學(xué)生問題解決能力，發(fā)展數(shù)學(xué)抽象素養(yǎng)。

1.4 教學(xué)重難點

教學(xué)重點：通過具體情境探索直線與圓的位置關(guān)系并利用其解決問題。

教學(xué)難點：通過問題情境抽象出判斷直線與圓的位置關(guān)系的關(guān)鍵要素，并會用符號表達(dá)。

2 教學(xué)片段

2.1 畫圖初探

“海上生明月，天涯共此時”，教師出示圓月從海平面冉冉升起的場景資料視頻。

師：你能用簡單的數(shù)學(xué)圖形例如我們學(xué)過的直線、圓等勾畫出這幅場景嗎？

生：能，將海平面看作是一條直線，將圓月看作一個圓。

師：很好，這位同學(xué)將海平面抽象地看作一條直線，將圓月抽象地看作圓，那么就請同學(xué)們在準(zhǔn)備好的學(xué)習(xí)紙上完成畫圖。（學(xué)習(xí)紙上已經(jīng)畫好了直線L）

師：“圓月從海平面冉冉升起”，大家發(fā)現(xiàn)這個動態(tài)過程中，什么在動？什么沒有動？你畫的圖怎樣體現(xiàn)這種變化？

生1：圓的大小有沒有要求？

生2：圓的位置有沒有要求？（受到生1的啟發(fā)提出）

設(shè)計意圖：讓學(xué)生在畫圖的過程中體驗、感知，并且通過學(xué)生提問的方式，促進(jìn)學(xué)生在活動中進(jìn)行思考，養(yǎng)成先思后做的習(xí)慣，這樣引導(dǎo)學(xué)生去畫出不斷變化的過程圖形，為后續(xù)總結(jié)分類做鋪墊。同時培養(yǎng)學(xué)生發(fā)現(xiàn)問題、提出問題的能力，提出問題的過程實際就是思考的過程，也是對圖形位置關(guān)系中重要要素的關(guān)注，這是對問題的第一次抽象。

2.2 動畫抽象

教師收集展示部分學(xué)生所畫的圖形。

師：你們能試著將大家所畫的圖形進(jìn)行分類嗎？

生3：直線與圓的位置關(guān)系可以分為三類。

師追問：你能說出這種分類的標(biāo)準(zhǔn)是什么嗎？

生3：看直線與圓的公共點的個數(shù)，第一種是直線與圓沒有公共點，第二種是直線與圓有兩個公共點，第三種是直線與圓只有一個公共點。

師：當(dāng)直線與圓無公共點、有兩個公共點時圖形特征明顯，但在第三種情形下你能確定此時只有一個公共點嗎？

教學(xué)說明：這個問題激起學(xué)生強(qiáng)烈地認(rèn)知沖突，看來用公共點的個數(shù)來刻畫直線與圓的位置關(guān)系有一定的局限性，有沒有其它更加準(zhǔn)確的方法來判斷直線與圓的位置關(guān)系呢？學(xué)生繼續(xù)觀察每個人所畫圖形的異同，得出的結(jié)論是所畫圓的位置不同，所畫圓的半徑不同，逐漸將所研究的數(shù)學(xué)對象的要素呈現(xiàn)出來。于是圓心到直線的距離d，圓的半徑r成為研究的關(guān)鍵要素，冰山一角逐漸浮出水面。

設(shè)計意圖：通過對比活動，讓學(xué)生感受直線與圓的位置可以從形的角度定性判斷，也可以從數(shù)的角度定量判斷，這是對問題的第二次抽象。

教師出示動態(tài)演示，利用幾何畫板度量d、r的值。

動畫1：圓定直線動，圓的大小位置不變，將直線逐漸平移，觀察直線與圓的位置關(guān)系。

動畫2：圓動直線定，保持圓的半徑不變，拖動圓心觀察圖形，接著保持圓心不動，改變半徑觀察圖形。

教學(xué)說明：學(xué)生經(jīng)歷了觀察、比較、動畫演示的過程后，已經(jīng)能夠清晰的看出問題背后的數(shù)學(xué)要素，并能將其抽象的用數(shù)學(xué)語言表達(dá)為當(dāng)d=r時，直線與圓只有一個公共點；當(dāng)d＜r時，直線與圓有兩個公共點；當(dāng)d＞r時直線與圓無公共點。反之亦然，至此，水到渠成地介紹了相切、相交、相離的相關(guān)概念。

設(shè)計意圖：通過圖形的變化，讓學(xué)生在變化的過程中發(fā)現(xiàn)變化的規(guī)律，在變化的過程中發(fā)現(xiàn)不變的本質(zhì)，滲透研究問題的方法——控制變量法，同時滲透數(shù)形結(jié)合的思想，這是第三次抽象。

2.3 典例賞析

例1：如圖2所示，已知∠AOB=30°，P為OB上一點，且OP=5 cm，以P為圓心，以R為半徑的圓與直線OA有怎樣的位置關(guān)系？為什么？

圖2

①R=2cm；②R=2.5cm；③R=4cm

變式：在 Rt△AOB 中，∠ABO=90°，∠AOB=30°，P為OB上一點，且OP=5cm，以P為圓心，以R為半徑的圓何時與AB相切？何時與OA相切？何時與邊OA有一個、兩個交點？

隨著圖形的變化，問題變得復(fù)雜，但無論怎樣變化，解決此類問題的關(guān)鍵是剝離出基本圖形，找準(zhǔn)半徑r、垂線段d及直線L。（如圖3）

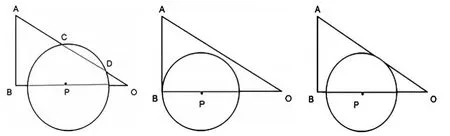
圖3

設(shè)計意圖：從較為復(fù)雜的圖形中剝離出基本圖形是關(guān)鍵，當(dāng)圓P的半徑發(fā)生變化時，圓與直線OA、AB相切形成對比，幫助學(xué)生理解和抽象基本圖形。圓與線段OA的交點隨著圓半徑的增大，交點的位置、交點的個數(shù)都發(fā)生了變化，為學(xué)生創(chuàng)設(shè)了運動變化的問題情境，幫助學(xué)生養(yǎng)成將動態(tài)問題靜態(tài)來看的研究方法及關(guān)注運動臨界值的意識。

3 教學(xué)反思

3.1 借運動變化展現(xiàn)思維過程

《課標(biāo)》指出要讓學(xué)生體驗從具體情境中抽象出數(shù)學(xué)符號的過程。［3］大部分教師往往只關(guān)注結(jié)果及結(jié)果的運用，而忽視了學(xué)生學(xué)習(xí)過程中思維的發(fā)展，本節(jié)課巧妙借助動畫演示，引導(dǎo)學(xué)生觀察、分析、抽象、概括，幫助學(xué)生從紛繁的現(xiàn)實情境中剔除無關(guān)因素，將問題中隱含的數(shù)學(xué)本質(zhì)凸顯出來，形成了理性思維品質(zhì)。

3.2 借運動變化滲透數(shù)學(xué)思想

《課標(biāo)》指出教學(xué)活動中要使學(xué)生逐步體會為什么要分類，如何分類，如何確定分類的標(biāo)準(zhǔn)。［4］這些目標(biāo)的達(dá)成不是靠一兩節(jié)課就能實現(xiàn)，它是一個長期滲透的過程。本節(jié)課通過學(xué)生畫圖、動畫演示，使學(xué)生經(jīng)歷了研究問題的過程，感受對于一個較為復(fù)雜的問題，采用分類討論辦法是一種較好的研究問題的策略，它能使復(fù)雜問題簡單化，分類的過程就是對事物共性的抽象過程，同時明確分類的標(biāo)準(zhǔn)可能不唯一，但每一種標(biāo)準(zhǔn)下的分類要不重復(fù)不遺漏。

3.3 借運動變化剝離幾何要素

在分類的過程中如何認(rèn)識對象的性質(zhì)，如何區(qū)別不同對象的不同性質(zhì)是教師要重點思考的問題。本節(jié)課采用控制變量法來研究問題，運用動態(tài)圖形演示，使得學(xué)生直觀地發(fā)現(xiàn)一個量的變化對于圖形間位置關(guān)系的改變所起的作用，從運動變化的角度辨證地看待問題，使得數(shù)學(xué)要素從問題背后浮現(xiàn)眼前，獲得基本圖形。在典例變式中，教師將問題在運動變化中進(jìn)一步拓展，使學(xué)生將研究問題的方式進(jìn)行遷移，學(xué)生的思維更加開闊，解決問題的能力逐漸增強(qiáng)。

3.4 借運動變化使數(shù)學(xué)抽象素養(yǎng)落地

發(fā)展學(xué)生數(shù)學(xué)素養(yǎng)是數(shù)學(xué)教學(xué)的使命擔(dān)當(dāng)。［5］課堂教學(xué)是落實數(shù)學(xué)學(xué)科素養(yǎng)的主渠道，教師應(yīng)努力挖掘教學(xué)內(nèi)容中可能蘊涵的育人價值，通過長期的教學(xué)實踐，逐漸培養(yǎng)和落實。本節(jié)課經(jīng)歷三次抽象，逐漸剝離出研究要素間的關(guān)系，并用數(shù)學(xué)語言表達(dá)，幫助學(xué)生形成理性思維，使數(shù)學(xué)抽象素養(yǎng)在課堂教學(xué)中落地。一線教師不能就教知識而教學(xué)，應(yīng)該站在數(shù)學(xué)學(xué)習(xí)的整體視角下思考教學(xué)，以具體知識為載體，為學(xué)生提供更加豐富的學(xué)習(xí)平臺，促進(jìn)學(xué)生學(xué)科素養(yǎng)的提升。

4 結(jié)語

學(xué)生數(shù)學(xué)抽象素養(yǎng)的發(fā)展不但是教學(xué)改革的要求所在，更是為了學(xué)生發(fā)展的需要。教師在教學(xué)過程中要思考創(chuàng)設(shè)恰當(dāng)?shù)那榫常侠砝脭?shù)學(xué)圖形來抽象問題，引導(dǎo)學(xué)生挖掘問題背后的數(shù)學(xué)要素，借助運動的變化讓培養(yǎng)核心素養(yǎng)落地于教學(xué)之中，幫助學(xué)生更好的學(xué)習(xí)并獲得更好的發(fā)展。