基于稀疏表示的陣列聲波測井儀數據無損壓縮傳輸方法

李 明,尹時松,張 寧,李波宏,莊獻華,李江山

(中國石油集團測井有限公司華北分公司,河北 任丘 062552)

作為一種重要的成像測井儀器，交叉多極子陣列聲波測井儀[1]將單極發射、接收陣列和偶極發射、接收陣列交叉組合；其中，單極子陣列包括關于井軸對稱、全方位的2個發射換能器和8個接收換能器，偶極子陣列包含正交放置的2個發射換能器和16個接收換能器。各個接收換能器記錄聲源發射后一定時間段內的聲波波列，通過時間-慢度相關方法[2]計算地層的縱波、橫波和斯通利波慢度，可用于識別巖性、計算巖石力學參數、識別氣層和裂縫，而由偶極陣列可得到地層快、慢橫波速度和方位，進行地層各向異性分析，已廣泛應用于碳酸鹽巖油氣層[3]、煤層氣[4]和致密砂巖氣層[5]的勘探開發。

陣列聲波測井儀聲波發射、接收換能器眾多，且采集聲波波列，因此儀器上傳地面的數據量很大。目前儀器僅有約42 kbit/s的最大電纜上傳速率，一旦提高儀器的測井速度，傳輸隊列中當前地層的測量數據在未上傳到地面系統的情況下，就會被新地層的測量數據覆蓋。因此，在井下儀器采用無損數據壓縮上傳是在采集數據不失真的同時，增加傳輸帶寬、提升儀器測井時效的有效方法。

目前主流的測井數據無損壓縮方法是LZW(Lempel Ziv Welch,藍波-立夫-衛曲)算法[6-9]，但LZW算法在編解碼過程中，需要存儲編碼字典，因此當非平緩變化數據流的信息冗余較少時，壓縮率較低；文獻[10]針對陣列聲波測井儀提出一種預測編碼方法，但沒有考慮聲波波列的數值時序分布規律，預測誤差編碼碼位較長，導致預測器性能不佳；文獻[11]提出一種基于BWT(Burrows-Wheeler Transform,伯羅斯-惠勒變換)和PPM(Prediction with Partial Matching,局部匹配預測)算法的陣列聲波數據無損壓縮傳輸方法，雖然考慮了聲波波列中數據分布規律，但算法復雜程度較高，要求實際應用中使用高性能的DSP硬件，且壓縮率最高只有51%，不能達到當前測井作業效率指標。

以上的壓縮方法都是基于傳統的信息熵減少理論，將聲波波列數據盡可能地轉換為平緩變化的數據流。如果從信號處理的角度考慮，將聲波波列從時間域轉換到某一變換域，且在該變換域，聲波波列只需極少的量值表征，那么井下上傳這些表征量值到地面系統，反變換后，就可恢復原始聲波波列。因此，從信號稀疏表示的角度出發，通過稀疏變換將聲波波列變換到其稀疏域。選擇恰當的稀疏變換矩陣，可使稀疏表示系數中非零元素個數遠小于波列長度。這里，采用K-SVD(K-means Singular Value Decomposition,K均值奇異值分解)算法，通過歷史聲波波列數據訓練稀疏變換矩陣。數據上傳時，將非零稀疏表示系數和重構波列與原始波列的誤差進行壓縮編碼上傳。在地面系統采用相同的稀疏變換矩陣進行反變換，再疊加誤差信息，恢復原始波列。通過HB油田陣列聲波仿真實驗、實測數據壓縮率比對和實際作業的應用測試，驗證方法在提升數據壓縮率和提高測井作業時效方面的有效性。方法的設計和開發有望提升陣列聲波測井的施工速度，為油田勘探的提質提效提供有力的技術支撐。

1 陣列聲波信號采集和傳輸原理

交叉多極子陣列聲波測井儀在一個深度點記錄12道單極子波列和32道偶極波列，包括8道單極子聲源T1發射，8個接收器采集的全波波列、4道單極子聲源T2發射，前4個接收器采集的全波波列和32道正交的兩個偶極子聲源交替發射，交叉放置的16個偶極接收器采集的偶極波列。

表1給出了GBG1井陣列聲波測量數據在一個深度點的存儲格式。由表1可以看到，單極子聲源T1發射采集的8道全波波列，存儲在曲線TFWV10中，總采樣點數為5376，每道波列點數則為672。同樣地，單極子聲源T2發射采集的4道全波波列，存儲在曲線TNWV10中，總采樣點數為832，每道波列點數則為208。而TXXWV10、TXYWV10、TYXWV10和TYYWV10則分別為采集的4個偶極分量，每個分量存儲8道全波波列，每道波列采樣點數為400。

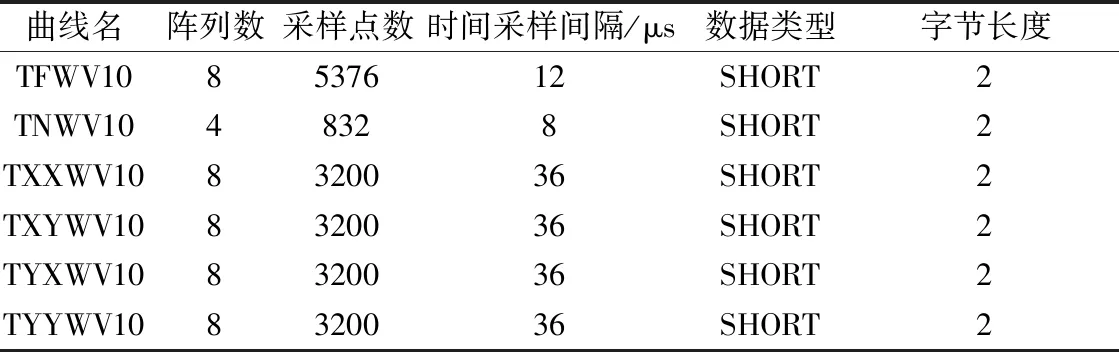
表1 GBG1井陣列聲波測量數據存儲格式

圖1給出了GBG1井TXYWV10曲線在3759.94 m深度處，采集的8道偶極波列。可以看到，各道全波波列具有較高的相似性。

圖1 GBG1井3759.94 m處 TXYWV10波形

如圖2所示，陣列聲波信號的數據上傳是通過遙測傳輸短節實現的。儀器采集的各道聲波全波列(一維時間信號)在井下儀器總線控制器的作用下，通過井下儀器總線，傳入遙測短節內進行緩存，形成上行數據幀。對數據幀進行PCM編碼后，轉換為模擬信號，經低通濾波和差分驅動，送入與傳輸電纜相連的模式變壓器，產生電纜中電壓的高低變化。地面系統在檢測到電纜電壓的變化后，經過信號濾波處理和模數轉換，以及PCM解碼，可接收到上傳的陣列聲波采集數據。由于高頻信號經測井電纜長距離傳輸后，幅度大幅衰減且信號嚴重失真，造成測井電纜傳輸帶寬有限。以陣列聲波數據傳輸為例，由表1可知波列每個采樣點的值為2 B長度的有符號SHORT型，計算一個深度點的陣列聲波采樣數據幀大小至少為37.125 KB，電纜上傳速率為41.66 kbit/s，則數據傳輸時間約為0.8911 s，加上聲源發射和陣列接收換能器采樣時間約為0.2 s，在不計入其他一維、二維采集數據的情況下，一次采集加數據上傳的時間至少為1.0911 s，而陣列聲波的深度采樣間隔為0.1524 m，可知儀器在單位深度地層的工作時長最小約為7.16 s。因此，在數據上傳前，對采集數據進行有效壓縮編碼，可大幅減少數據上傳時間，變相增加單位時間內傳輸的數據量和電纜上傳帶寬，進而減小儀器在單位深度地層的工作時長。

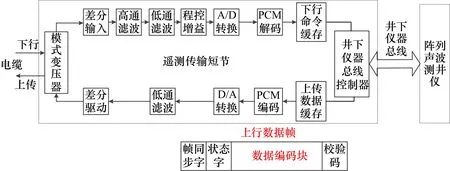
圖2 陣列聲波測井儀數據傳輸原理框圖

2 陣列聲波采集數據無損壓縮方法

2.1 信號稀疏表示原理

由信號稀疏表示理論可知，如果原始信號是稀疏的，則可以將其用一稀疏正交基和非零個數遠小于信號序列長度的稀疏系數序列線性組合表示，即稀疏變換[12]；而作為稀疏變換矩陣的稀疏正交基，稱為稀疏字典，可拓展為超完備的冗余字典。對原始信號f進行稀疏變換：

α=Df

(1)

式中:f∈RN×1為N個采樣點的等間隔采樣原始信號；D∈RM×N為稀疏變換矩陣；α∈RM×1為f進行稀疏變換的稀疏表示系數，如果M=N，則D為稀疏字典；如果M?N，則D為超完備冗余字典。反變換有f=DHα，DH為D的共軛轉置陣，滿足DHD=1。

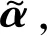
(2)

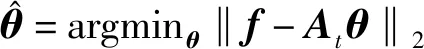
2.2 基于稀疏表示的聲波全波列數據壓縮方法

基于稀疏表示的聲波全波列數據壓縮方法原理如圖3所示。

圖3 聲波全波列數據無損壓縮方法原理框圖

首先，提取一道的聲波全波列數據，去除基值后，根據采用K-SVD算法預先構建的過完備冗余字典B和正交匹配追蹤算法，計算稀疏表示系數向量A，對向量A中的數值取整后，再根據稀疏反變換，重構波列，得到原始波列與重構波列的誤差向量err。將取整后的向量A和誤差向量err中的非零值、索引和基值Base整合，形成二進制數據流，采用自適應算術編碼后上傳。在地面系統，根據解碼后的稀疏表示系數和字典B進行稀疏反變換，得到波列估計值，再加上解碼后的誤差和基值，就可以完全恢復出原始的聲波全波列。由于原始波列值為16位整型數，因此向量A和誤差向量err中的非零值和索引值同樣為16位整型。

算術編碼是一種信息保持型編碼，無需向LZW算法傳送編碼字典，因此壓縮率有了明顯提升。算術編碼符合概率匹配原則：出現概率較大的符號壓縮為較短的碼字，出現概率較小的符號取較長碼字。自適應算術編碼根據編碼時符號出現的頻繁程度動態修改信源符號的概率。當出現某個符號在整個符號流中全局概率較小，但在符號流某一位置集中分布的情況時，宜采用自適應編碼；由于符號出現的概率隨著符號輸入不斷變化，輸入相同符號數越多，該符號的概率被更新得越大，則該符號壓縮后的碼字要明顯小于需要遍歷的整個符號流，統計每個符號全局概率的固定模式算術編碼。因此，采用編碼過程中動態估計字符概率的自適應算術編碼不僅在壓縮算法時效上優勢明顯，而且壓縮率也優于固定模式編碼。

2.3 基于K-SVD的稀疏變換矩陣訓練方法

信號的稀疏度與超完備冗余字典(稀疏變換矩陣)密切相關，選用符合聲波波列特征的稀疏變換矩陣，可使聲波波列在該稀疏變換矩陣下表示更稀疏。因此，采用K-SVD算法[15]，以歷史多道聲波全波列為訓練數據，預構建更符合聲波波列特征的過完備冗余字典，可在提高聲波波列稀疏度的基礎上，進一步提升聲波波列的重構精度，減少誤差向量非零值數目，從而使編碼數據量更小。

稀疏變換矩陣D∈RN×L(L>N)，矩陣中列向量為字典原子，訓練數據集X∈RN×S，X中的列向量即為一道訓練用的聲波全波列數據，其中L為字典原子個數，S為訓練用聲波全波列道數。訓練過程中稀疏表示系數向量集為Γ∈RL×S。K-SVD算法的目標函數為

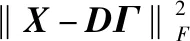
(3)

式中:γi為向量集Γ中第i個列向量；K為稀疏表示系數向量中非零分量個數的最大值。K-SVD算法的訓練為一個迭代過程，首先給定初始矩陣D，采用正交匹配追蹤算法求解訓練數據集X的稀疏表示系數矩陣Γ；再根據Γ，更新矩陣D。重復進行稀疏表示系數矩陣求解和稀疏變換矩陣更新兩個步驟，直至滿足式(3)的迭代條件。稀疏變換矩陣需要逐一更新矩陣D中的列。假設更新D中的第j個列向量dj，計算去掉該列代表的原子成分在所有S個訓練樣本中造成的誤差

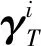
Ej=UΔVT

式中:U為N×N維矩陣;V為S×S維矩陣;U和V是酉矩陣，與本身轉置矩陣相乘等于單位陣;Δ為N×S維矩陣，其主對角線上的元素為奇異值，且除主對角線上的元素以外全為零值。更新dj為U的第1列，計算V的第1列和Δ(1,1)的乘積，更新矩陣Γ中與列向量dj對應的第j行中非零元素值。

3 實驗結果分析和現場測試

3.1 仿真實驗結果和分析

在仿真實驗中采用COMSOL軟件，模擬陣列聲波儀器分別在快速地層(花崗巖)、標準地層(砂巖)和慢速地層(泥巖)的陣列聲波單極子接收換能器響應。其中，模擬儀器源距為3.0 m，接收換能器間距為0.15 m，聲源采用中心頻率為10 kHz的Ricker子波。圖4給出了快速地層中儀器8個接收換能器響應波形。

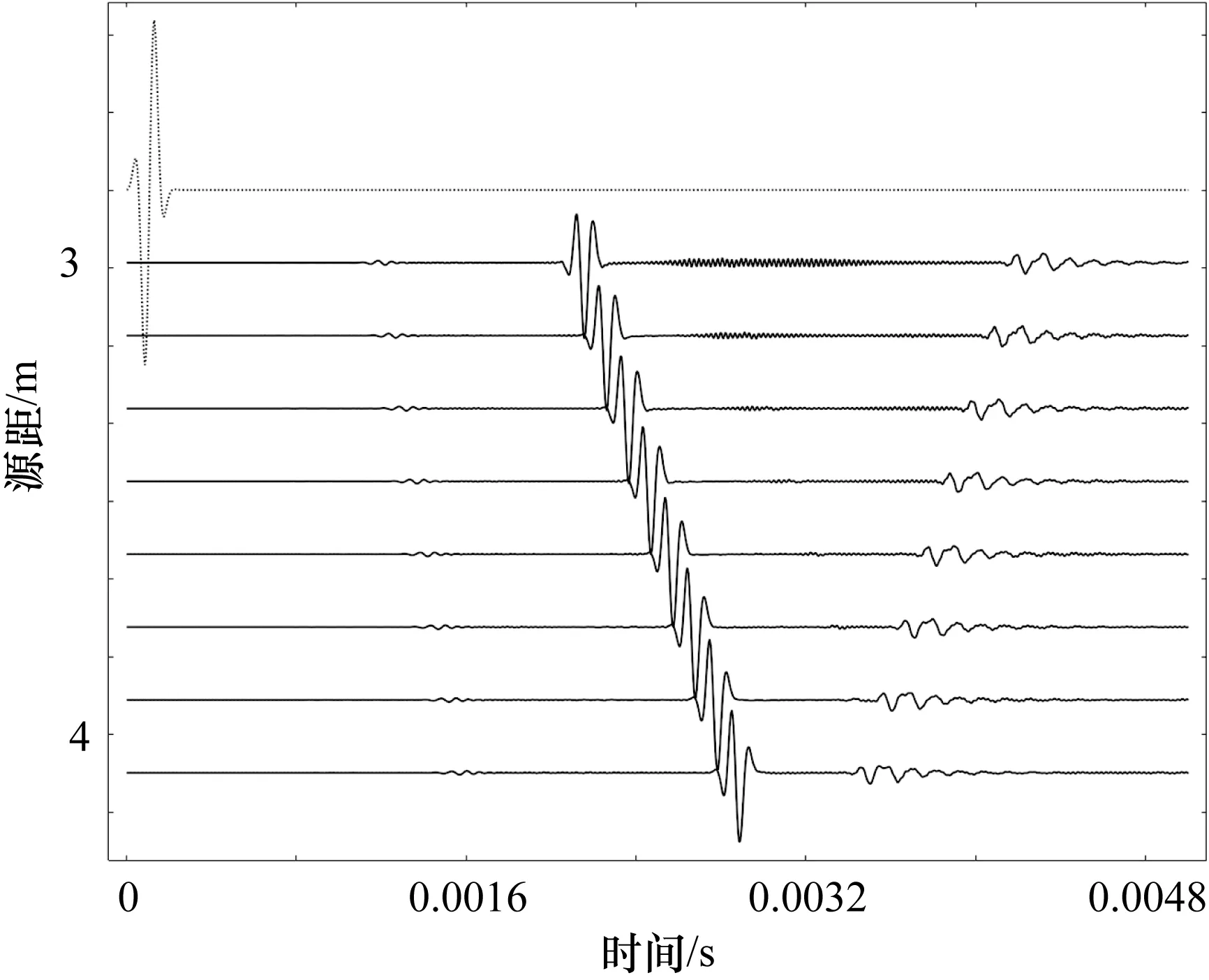
圖4 快速地層中8個接收換能器響應波形

如圖4所示，最上部的虛線波形為聲源發射波形，源距3～4 m處從上至下分別為8道接收換能器波形。實驗中，共模擬3種地層接收波形176道，采用175道全波列波形構建K-SVD算法的訓練樣本集。初始過完備冗余字典采用DCT矩陣，原子數設為128，訓練稀疏度上限為50，訓練迭代次數為100。圖5和圖6分別給出了1道未參與訓練的聲波波列采用正交匹配追蹤算法在訓練后冗余字典和原始Hadamard字典上的重構波形、稀疏表示系數和與原始波列的誤差。

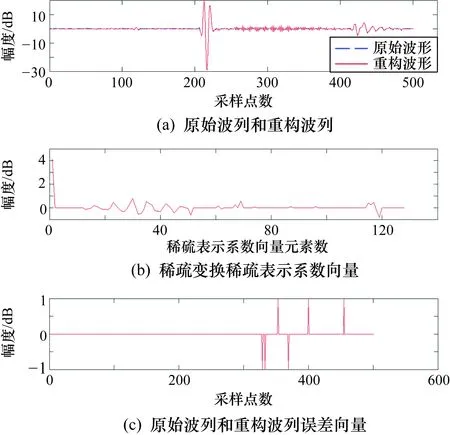
圖5 仿真實驗訓練后冗余字典上的波列重構結果

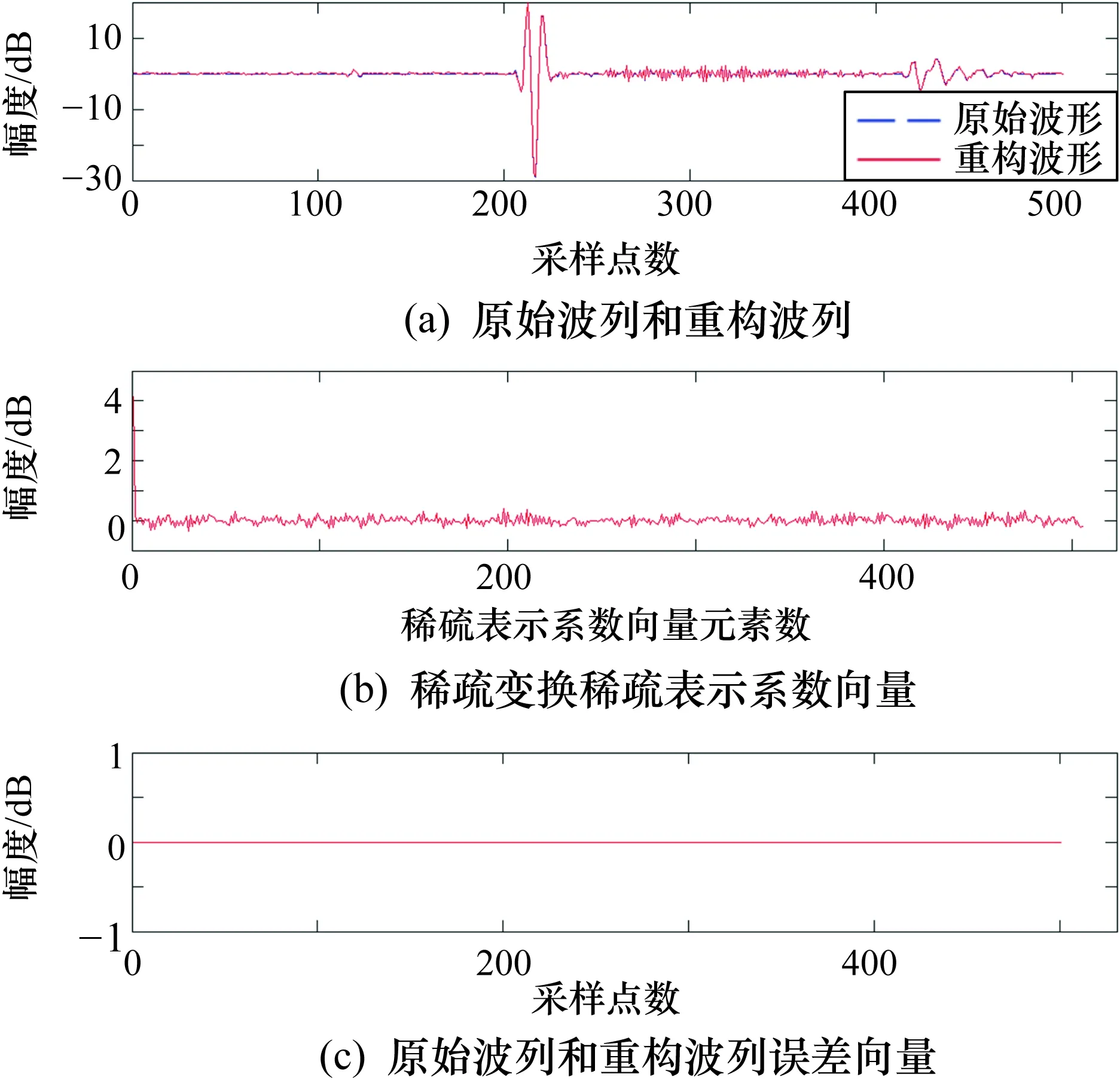
圖6 仿真實驗原始Hadamard字典上的波列重構結果

這里，換能器接收波列長度為501，原始Hadamard字典的原子數為512。由圖5和圖6可以看到，重構波列和原始波列基本一致，但訓練后冗余字典上的波列稀疏度為49，明顯優于原始Hadamard字典上的波列稀疏度398。由于Hadamard字典的原子數大于K-SVD算法的過完備冗余字典原子數，因此原始Hadamard字典上的波列誤差向量為0，優于訓練后冗余字典上的誤差向量。模擬數據壓縮過程，一道原始波列為501×2 B，而經稀疏變換后，稀疏表示系數的非零值與索引值占49×4 B，加上非零誤差值和索引的6×4 B，再加上波形基值2 B和標準化用到的波形最大和最小值4 B，共226 B，不考慮二進制數據流最后的自適應算術編碼，則一道原始波列的最小壓縮率可達到77.45%。仿真實驗驗證了采用K-SVD算法訓練冗余字典的有效性。

3.2 實際測井數據實驗結果和分析

本文采用GBG1井TFWV10曲線中4000～4038 m深度范圍內的2000道聲波全波列數據構建K-SVD算法的訓練樣本集，初始過完備冗余字典采用Hadamard矩陣，原子數設為1024，訓練稀疏度上限為50，訓練迭代次數為100。圖7給出了該訓練樣本集上的迭代誤差，這里對每個訓練樣本進行數據標準化，范圍為[-1，1]。由圖7可以看到，在保證聲波全波列稀疏變換稀疏度的情況下，隨著字典更新次數的增加，算法的均方根誤差逐步減少，說明了K-SVD算法的收斂性。

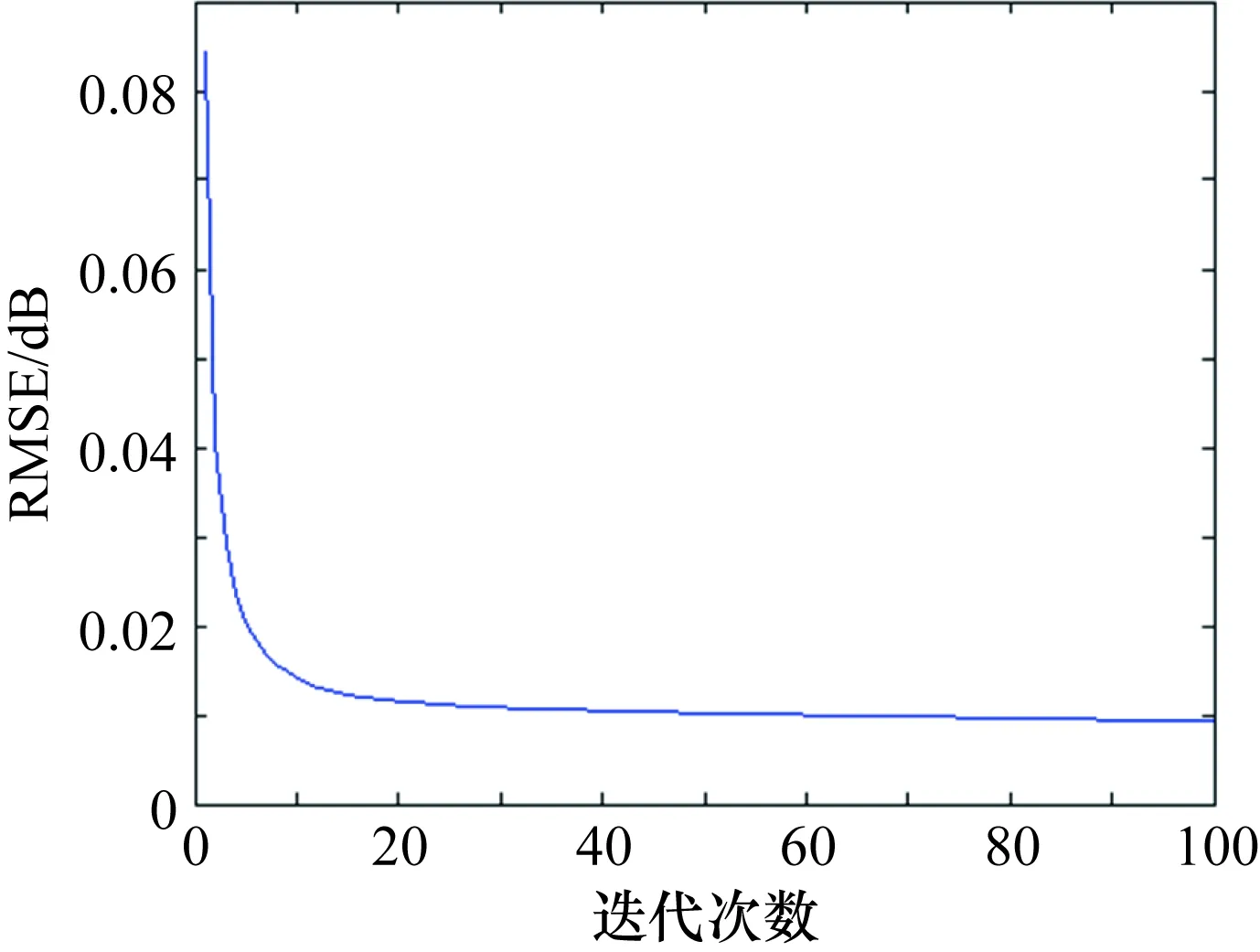
圖7 K-SVD算法迭代誤差

隨機提取GBG1井TFWV10曲線中在訓練用全波波形數據深度范圍外的一道聲波波列，進行數據無損壓縮算法實驗，驗證K-SVD算法的有效性。圖8和圖9分別給出了該聲波波列采用正交匹配追蹤算法在訓練后冗余字典和原始Hadamard字典上的重構波形、稀疏表示系數和與原始波列的誤差。

圖8 訓練后冗余字典上的波列重構結果

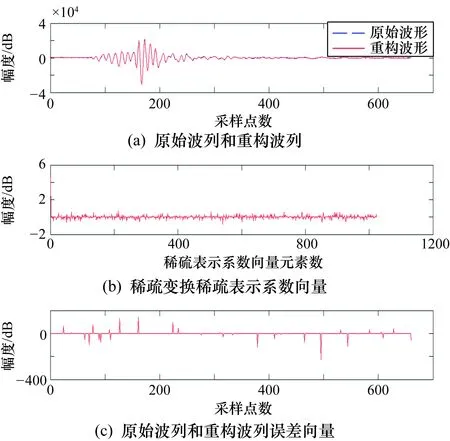
圖9 原始Hadamard字典上的波列重構結果

由圖8和圖9可以看到，在兩個冗余字典上的重構波列與原始波列基本一致，原始波列和重構波列的誤差向量(圖8(c)和圖9(c))也驗證了這一點，統計平均誤差分別為0.98%和1.65%；雖然兩個誤差近似，但比較圖8(b)和圖9(b)的稀疏表示系數向量，發現在訓練后冗余字典上的稀疏度明顯優于原始Hadamard字典；在訓練后冗余字典上的稀疏表示系數向量中非零值個數為94，而在原始Hadamard字典上的相應值為444，驗證了筆者提出的無損壓縮算法中對于冗余字典進行預訓練步驟的必要性和有效性。模擬數據壓縮過程，一道原始波列為660×2 B，而經稀疏變換后，稀疏表示系數的非零值與索引值占94×4 B，加上非零誤差值和索引的37×4 B，再加上波形基值2 B和標準化用到的波形最大和最小值4 B，共530 B，不考慮二進制數據流最后的自適應算術編碼，則一道原始波列的最小壓縮率可達到59.85%。

針對HB油田FY1井等3口井的實測陣列聲波數據，比較本算法與LZW算法、算術編碼和文獻[11]算法的數據壓縮率，結果如表2所示。其中，算法分別針對TFWV10、TNWV10兩種單極子波列和偶極接收波列，訓練3種過完備冗余字典。

由表2可以看到，筆者算法的壓縮率在不同數據類型上是最高的，較文獻[11]算法的壓縮率平均提升了約17.3%。其中，隨著數據文件變大，LZW算法的壓縮率有所提升，這是由于數據流中重復字符串的增多，使得字典中對應字符串編碼縮短導致的。對于筆者算法，可以看到，在TNWV10數據上的壓縮率略優于在TFWV10和偶極波列數據上的壓縮率，這是由于TNWV10數據的全波波列長度小于256，因此在壓縮時，誤差的索引值只占用1 B，導致碼流長度減少，壓縮率增加。同時，P273井4種方法的壓縮率較其他兩口井在整體上有明顯提升。經該井實驗數據研究發現，測量井段對應地層中出現各向異性極弱的大段泥巖層，使得單極子接收波列和偶極子接收波列各道全波波列具有高度相似性，則LZW算法構造的編碼字典大幅度減小，算術編碼由于字符出現概率增大，編碼碼字縮短，導致兩種算法的壓縮率明顯增加。由于二進制碼流中，字符變化的規律性增強，也使得文獻[11]算法的壓縮率增加。對于筆者算法，波列的高度相似性導致訓練的冗余字典更能表征波列特征，使得壓縮時稀疏變換的稀疏度和重構精度增加，壓縮編碼長度進一步降低。

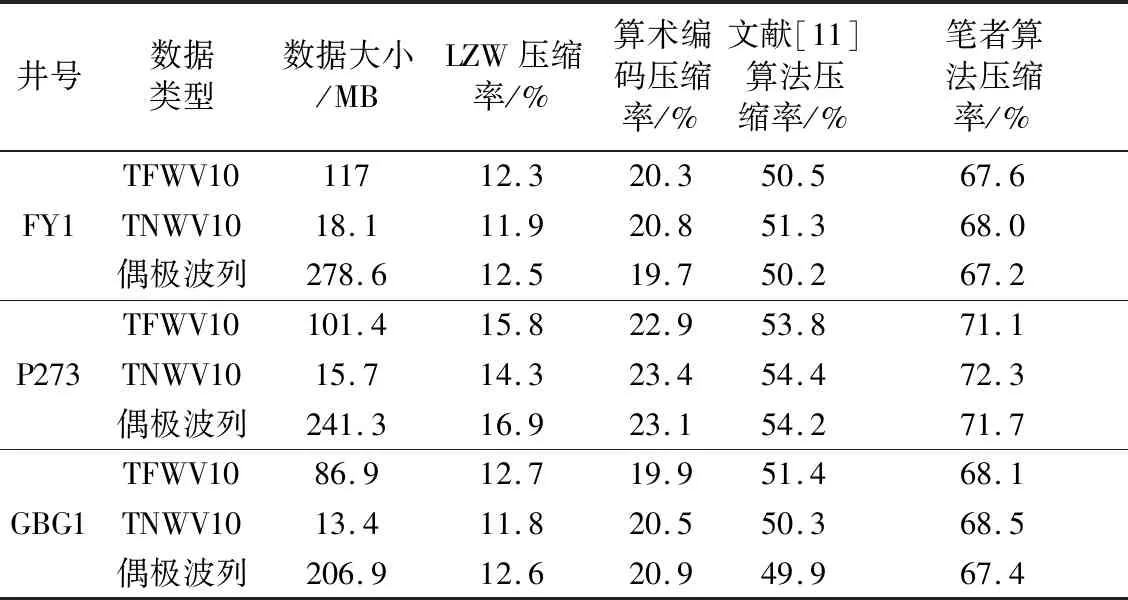
表2 算法壓縮率實驗結果

3.3 實際作業應用測試

重新設計的SL6680型陣列聲波測井儀，應用無損壓縮傳輸方法在HB油田GuGu8井等測井作業井眼環境較好的4口井進行了陣列聲波實際作業應用測試。在應用測試過程中，對于同一口井分別采用原有的SL6680型儀器和新系統進行測井時效對比測試，結果如表3所示。

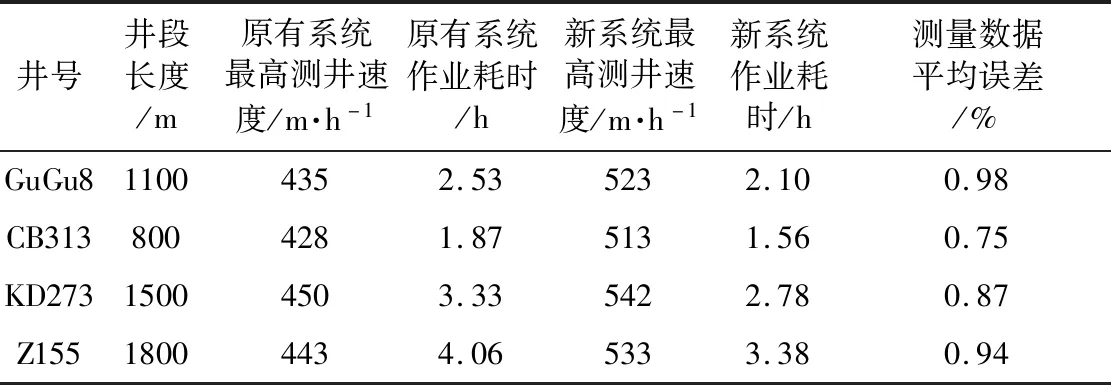
表3 測井時效對比

由表3可以看出，原有儀器和新系統的測量數據平均誤差在測井重復測量標準規定的數據誤差范圍內，說明兩者的測量數據幾乎相同。在這種情況下，新系統的最高測井速度整體高于原有儀器，測井作業耗時大幅度縮短。經數據統計計算，新系統的測井效率較原有儀器平均提升了約20.2%。

4 結束語

針對陣列聲波測井儀器，對采集的多道單極子和偶極子全波波列，采用基于信號稀疏表示的數據無損壓縮傳輸算法，在數據傳輸帶寬受限的情況下，有效提升單位時間內的上傳信息量，最終提高了測井時效，使陣列聲波測井儀器在保證采集數據不失真的條件下，滿足油田勘探提質提效的形勢需求。