移動機器人RRT算法改進研究

符秀輝,劉 然

(沈陽化工大學 信息工程學院,遼寧 沈陽 110142)

快速搜索隨機樹(Rapidly-Exploring Random Trees，RRT)算法由美國愛荷華州立大學Steven M.LaValle教授在1998年提出，RRT的思想是快速擴張一群像樹一樣的路徑以探索(填充)空間的大部分區域，伺機找到可行的路徑。RRT算法的特點是能夠快速有效地搜索高維空間，通過狀態空間的隨機采樣點，把搜索導向空白區域，從而尋找到一條從起始點到目標點的規劃路徑，適合解決多自由度機器人在復雜環境下和動態環境中的路徑規劃。對RRT算法的改進也有很多，施楊洋等[1]使用雙樹RRT算法在障礙物周圍生成了若干節點，并在這些節點中引入了斥力，生成多棵局部隨機樹，使局部隨機樹向遠離障礙物方向擴展，減少了局部隨機樹對障礙物的檢測次數和擴展過程中對障礙物的檢測時間，加快了算法的收斂速度，改善了算法的偏差性；劉恩海等[2]使用自適應策略改變引力系數的大小從而改變步長，引導隨機樹朝目標點方向高質量地生長，并解決了目標振蕩和隨機樹在障礙物附近聚集的問題，使RRT算法具有一定的可行性和有效性，有效縮短了路徑規劃時間；成怡等[3]引入了變概率目標偏向思想，通過設置算法認定目標點是局部目標點的概率閾值方法，在每次生成隨機點之前隨機生成概率值，與概率閾值做比較，如果高于閾值，則將生成的隨機點作為擴展樹子節點的生長目標點，反之則采用基本RRT算法中隨機生成的節點作為擴展樹子節點的生長目標點，克服了隨機擴展樹生長時采樣的隨機性和收斂速度慢的問題；徐秉超等[4]采用預生長方式選擇步長，基于Metropolis接受準則的隨機點篩選機制，對受時間影響而形成的不同生長可能性區域進行劃分，在一定程度上解決了隨機搜索樹的重復生長問題，令重要障礙物產生斥力，使機器人避開障礙物，減小了勢場計算規模，提高了路徑規劃的避障效率；喬慧芬等[5]利用人工勢場法在初始環境中預規劃一條初始路徑，在新出現的障礙物周圍確定合適的規劃空間，利用RRT算法規劃局部路徑。最后，合并初始路徑與局部路徑得出最終路徑，減小了路徑長度，縮短了規劃時間。本文針對RRT算法存在隨機性強、偏差大、路徑不一定最優等缺點，對RRT算法進行改進研究，借助人工勢場法，加入自適應策略，不斷改變步長大小，最終使機器人加速到達目標點，減小耗時，提高RRT算法的執行效率。

1 RRT算法

RRT算法是以一個初始點作為根節點，通過隨機采樣增加葉子節點的方式，生成一個隨機擴展樹。當隨機樹中的葉子節點包含了目標點或機器人進入了目標區域后，則在隨機樹中找到一條從初始點到目標點的路徑，并在狀態空間中對采樣點進行碰撞檢測，使機器人能夠避開障礙物。

在二維空間中，以初始點作為根節點，生長隨機樹，并建立隨機節點列表。如果隨機節點在空閑空間上，則通過歐氏距離公式計算找到隨機節點距離隨機節點最近的樹節點，再通過滿足步長限制的中間節點隨機擴展一定步長并生成新節點，期間與中間點進行碰撞檢測。如果與中間點存在障礙物，則重新尋找新節點；如果不存在，則將這個新節點加入到隨機樹中。當隨機樹中的子節點包含目標點時，則在隨機樹中生成一條由起始點到目標點的路徑；如果發生碰撞，則放棄這次擴展，其生長方式如圖1所示。

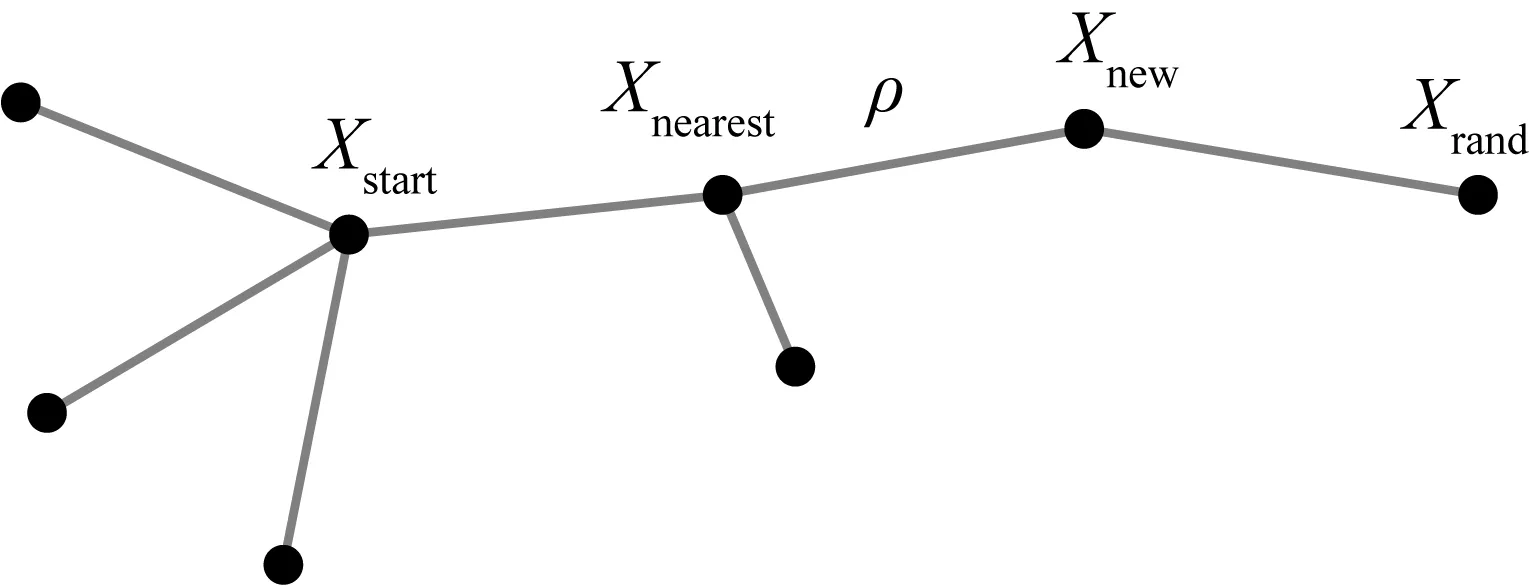
圖1 RRT隨機生長方式

2 自適應RRT算法

針對RRT算法的隨機性強、搜索沒有目的性、路徑不一定最優的缺點，提出借助人工勢場引力函數思想，改進節點的生成方式，對隨機樹中的每個節點xn都增加一個目標引力函數G(n)，此處的節點xn表示由起點xstart(或終點xgoal)向外擴展的第n個節點xnew。其公式可表示為

F(n)=R(n)+G(n)

(1)

式中：F(n)為從節點n到目標點的生長指導函數；R(n)為從初始節點到節點n的隨機生長函數。

胡兵等[6]和成浩浩等[7]對RRT算法中的節點進行了改進。在改進RRT算法過程中產生的新節點xnew由隨機樹節點xrand和目標節點xgoal共同決定。如圖3所示，在二維空間下，定義沿隨機點xrand擴展方向的點為x1，步長為ρ，沿目標點xgoal擴展方向的點為x2，步長為kρ，k為系數，目標點方向則由x1、x2共同決定，通過調節系數k使新節點不斷向目標點偏移，最終到達目標點。

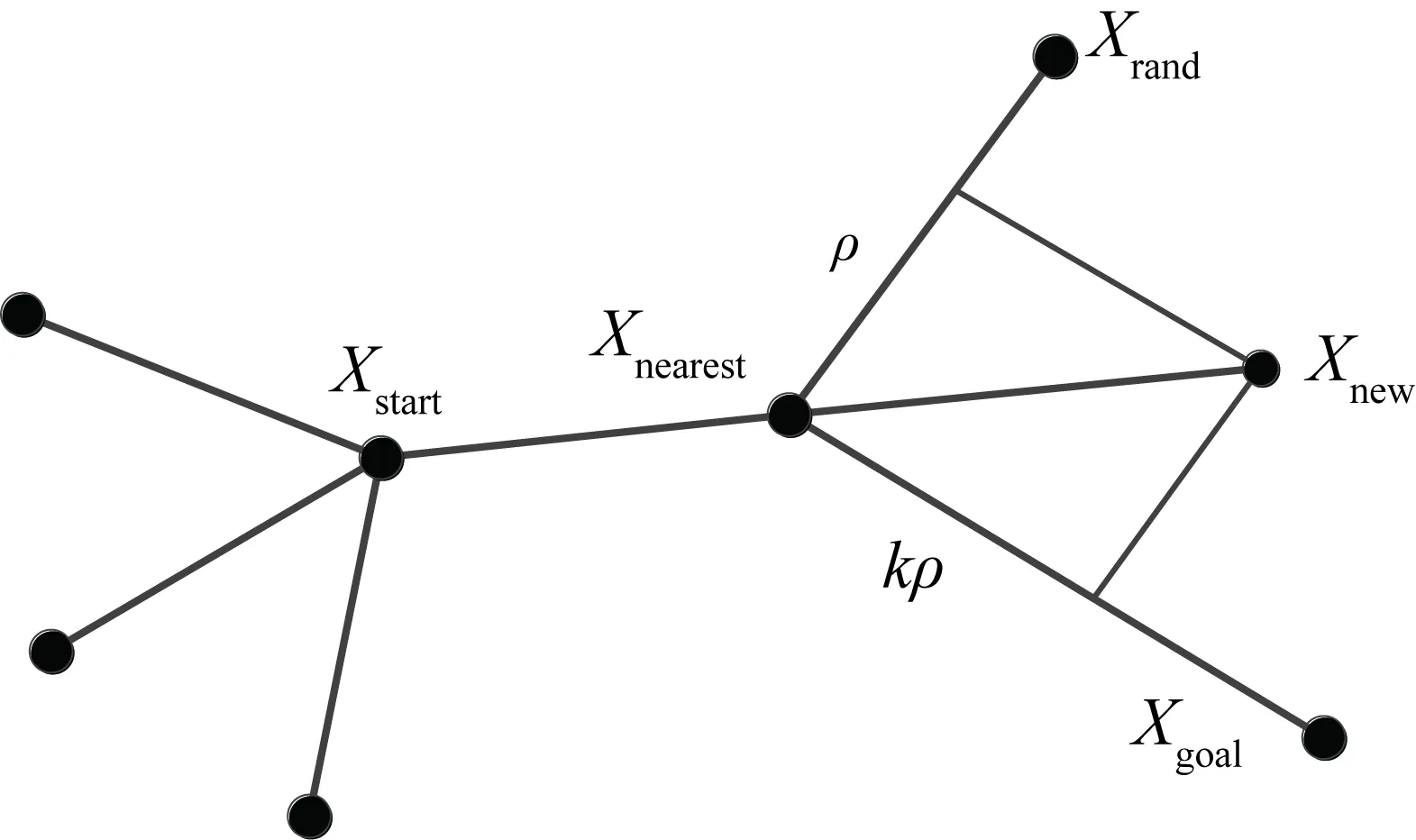
圖2 RRT改進節點生成方式

沿隨機點擴展方向點x1的坐標表達式為

(2)

目標點擴展方向點x2的坐標表達式為

(3)

式中：‖xrand-xnearest‖為隨機點到距離隨機節點最近的樹節點的距離的絕對值；‖xgoal-xnearest‖為目標點到距離隨機節點最近的樹節點的距離的絕對值。

因此，根據式(1)可得新節點xnew的坐標表達式：

xnew=xnearest+x1+x2

(4)

為了解決機器人耗時長的問題，王洪斌等[8]和徐飛[9]在人工勢場中引入了相對速度，分別作為優化路徑和排除對機器人路徑規劃影響很小的障礙物的指標。楊凱等[10]在人工勢場法中增加了虛擬目標并考慮了阻力的影響。本文對沿目標點擴展方向的點x2做出改變，使其系數k與引力的大小有關。當機器人距離目標點遠時，k增大；當機器人距離目標點近時，k減小，直至引力為零，從而避免隨機樹節點到達目標點時發生振蕩[11]。其具體過程如下，定義引力勢場函數表達式為

U(q,v,a)=εa‖q-qgoal‖m+εb‖v-vgoal‖n+εc‖a-agoal‖l

(5)

式中：εa、εb、εc為系數；m、n、l為正常數。對應引力函數表達式為

F(q,v,a)=F(q)+F(v)+F(a)

(6)

其中：

(7)

式中：Xq、Xv、Xa分別為機器人相對目標點的位置、速度和加速度的單位向量。

系數k的表達式為

k=λ‖F‖

(8)

式中：λ為正常數；‖F‖為引力的絕對值，可以進行測量，它與機器人相對目標點的位置、速度和加速度有關。

因此，得到新節點xnew的坐標表達式為

xnew=xnearest+x1+x2

(9)

3 實驗結果與分析

機器人小車如圖3所示，用STM32F103ZET6進行控制，外設采用激光雷達、里程計、慣性導航IMU、電機等，利用激光雷達Rplider A1進行測距，利用MPU6050測量偏航角度，進而得到小車的坐標，通過編碼器對機器人運行時的車輪運行圈數計數，測量機器人運行時的速度，通過編碼器對機器人速度形成閉環控制，對單位時間內的速度進行積分和微分計算，即可得到機器人運行的實際距離和加速度。移動小車實驗場景按照圖4所示位置進行布置，黑色區域是障礙物位置，為了使實驗數據更具說服性，必須使機器人從障礙物之間的狹窄通道通過，減少其他因素的影響[11]，為此實驗進行50次，將RRT算法和自適應RRT算法進行實驗對比，如圖4和圖5所示。實驗中相關參數設置如下：xstart=[2,2]，xgoal=[18,18]，εq=εv=εa=1，m=n=l=2，λ=1，小車初始速度為0.3 m/s，角速度設置為0.5 rad/s。

圖3 移動小車

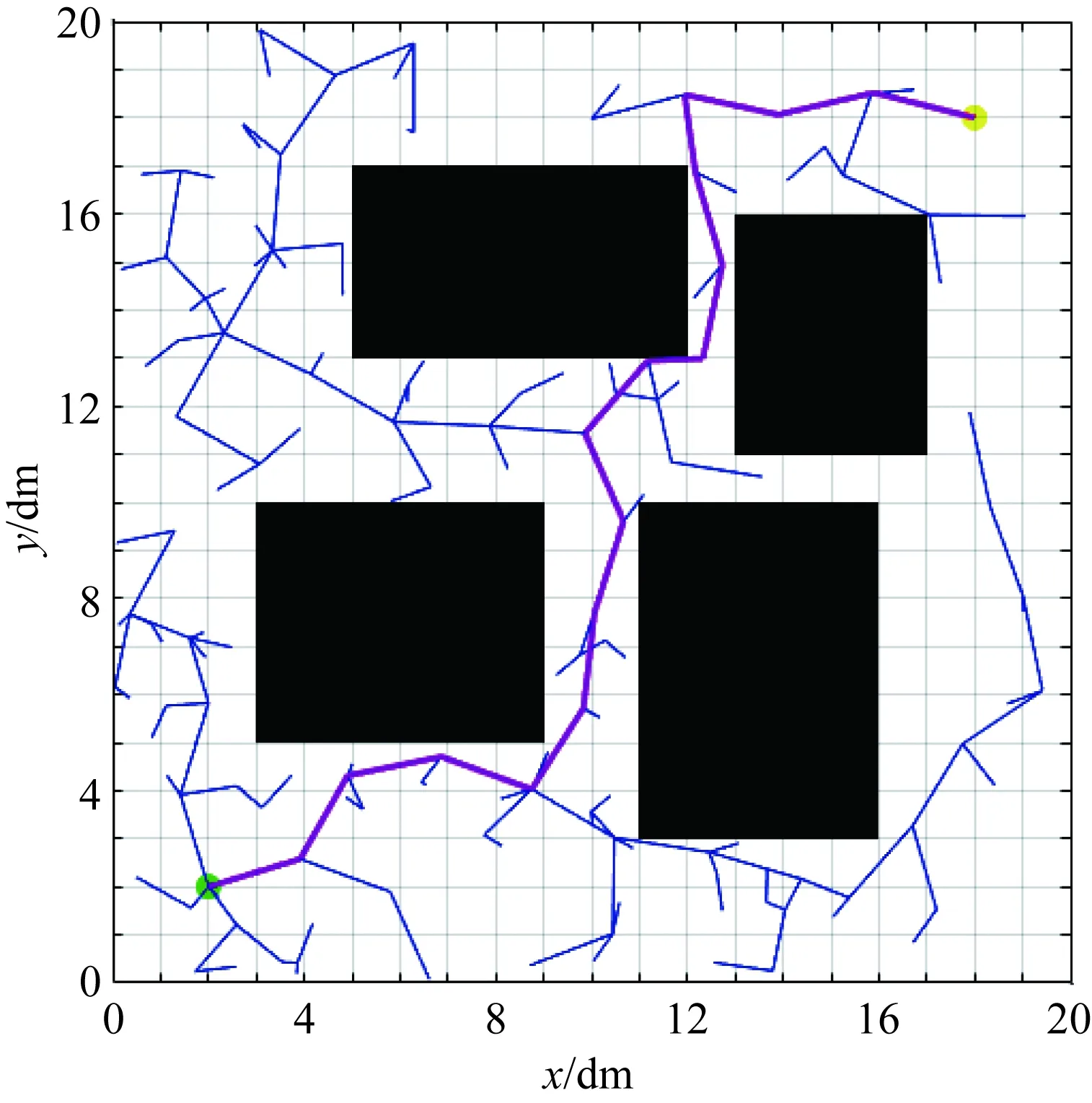
圖4 RRT算法

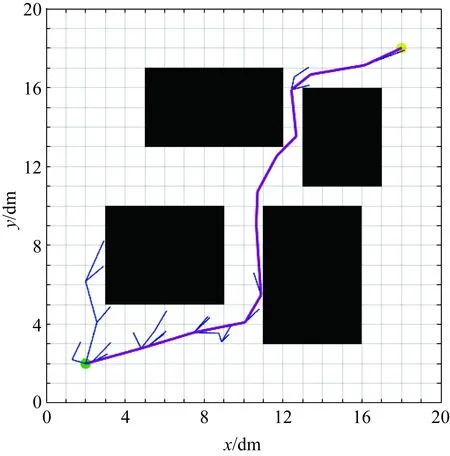
圖5 自適應RRT算法

在加入了自適應策略的RRT算法中，不斷調整系數k，使機器人逐漸向目標點靠近，只要機器人不達到目標點，則x≠xgoal或v≠vgoal或a≠agoal總存在，因此式(9)總成立。經多次實驗，RRT算法和自適應RRT算法耗時比較如圖6所示。

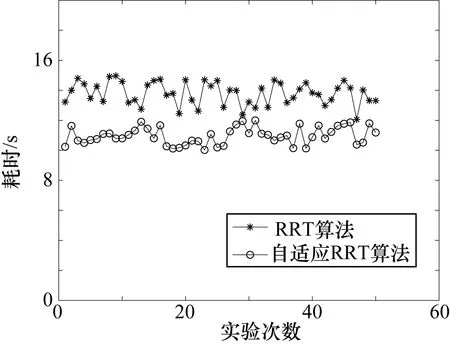
圖6 兩種方法耗時比較

實驗結果表明自適應RRT算法可以有效地節省時間，更具有目的性且偏差較小，其分析結果如表1所示。

表1 兩種方法耗時對比

由表1可知，自適應RRT算法相比于RRT算法節省了20.45%的時間。

4 結束語

本文在RRT算法中借助人工勢場法，加入了自適應策略，不斷改變節點步長的大小，使機器人快速安全到達目標點。由于RRT算法本身的缺陷，會導致路徑不斷變化，為了減小這種影響，必須使小車行駛在同一路段，從障礙物中間通過并躲避障礙物，而不能從地圖邊緣到達目標點。實驗結果表明，自適應RRT算法相比于RRT算法在實際應用中耗時明顯減少，可以極大地提高機器人作業效率，有效地節省了時間。目前實驗本身仍然存在的問題是算法只適用于比較規則的障礙物，對不規則的障礙物來說，有很多凹凸點，容易使機器人重復作業陷入死區，因此應對障礙物中凹凸點處進行研究，使機器人適用于更多場合，并對算法和路徑進行優化，從而使機器人小車快速安全地到達目的地。