圈與圈克羅內克乘積圖羅馬{3}-控制

高 紅， 黃 佳 歡， 劉 仁 邦， 楊 元 生

(1.大連海事大學 理學院，遼寧 大連 116026；2.大連理工大學 計算機科學與技術學院，遼寧 大連 116024 )

0 引 言

給定圖G=(V，E)，V是圖G的頂點集合，E是圖G的邊集合．集合N(v)={u|uv∈E}稱為頂點v的開鄰域．圖G的頂點個數稱為階．頂點v的度dG(v)為N(v)中包含的頂點個數，最大/小度記為Δ(G)/δ(G)．

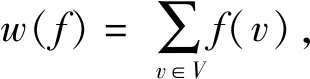
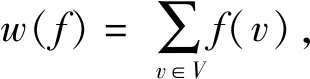
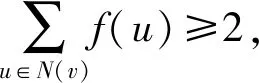
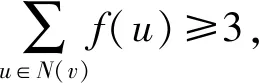
本文研究圈與圈克羅內克乘積圖的羅馬{3}-控制數，給出圈與圈克羅內克乘積圖羅馬{3}-控制數的上界和下界．通過構造可遞推的羅馬{3}-控制函數可以得到圈與圈克羅內克乘積圖羅馬{3}-控制數的上界．結合前人給出的一般圖羅馬{3}-控制數的下界，可以得到圈與圈克羅內克乘積圖羅馬{3}-控制數的下界．

1 圈與圈克羅內克乘積圖Cn×Cm

圈Cn與圈Cm克羅內克乘積圖Cn×Cm是一個有mn個頂點的四正則圖，其頂點集合和邊集合分別為V(Cn×Cm)={vi，j|0≤i≤n-1，0≤j≤m-1}，E(Cn×Cm)={ei，j|ei，j=(vi，jvi-1，j+1)，0≤i≤n-1，0≤j≤m-1}∪{e′i，j|e′i，j=(vi，jvi+1，j+1)，0≤i≤n-1，0≤j≤m-1}，其中下標i和j分別對n和m取模．圖1(a)表示圖C3×C6，圖1(b)表示其上的一個羅馬{3}-控制函數，圖中的數字表示的是f(vi，j)．

設G=Cn×Cm，f為圖G上的羅馬{3}-控制函數，則f可表示為

例如：

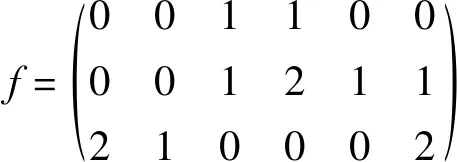
表示C3×C6上的羅馬{3}-控制函數，其圖形如圖1(b)所示．

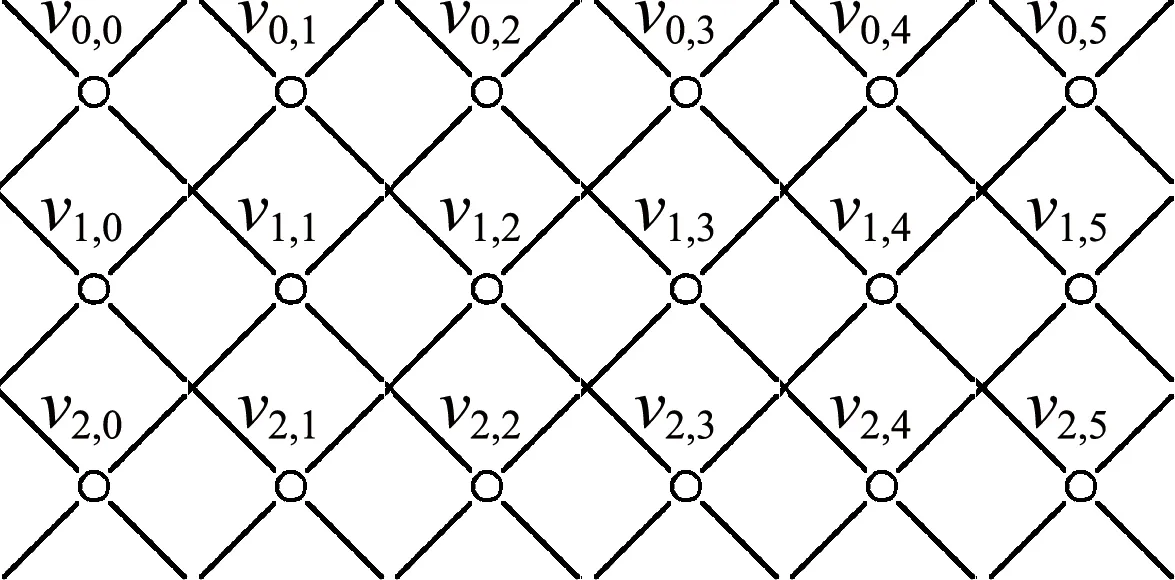
(a)C3×C6

2 Cn×Cm羅馬{3}-控制數的界

2.1 Cn×Cm羅馬{3}-控制數的下界

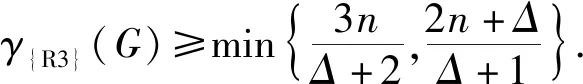
若G=Cn×Cm，則圖G的階數為mn，最大度Δ(G)=4，由定理1可得下面的推論．

推論1若G=Cn×Cm，當m，n≥3時，則有γ{R3}(G)≥mn/2．

2.2 Cn×Cm羅馬{3}-控制數的上界

定理2對于任意的正整數m≥3，G=C3×Cm的羅馬{3}-控制數上界為

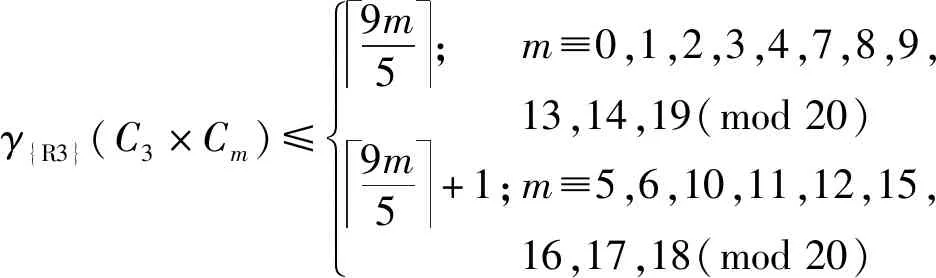
γ{R3}(C3×Cm)≤9m5;m≡0,1,2,3,4,7,8,9,13,14,19(mod20)9m5+1;m≡5,6,10,11,12,15,16,17,18(mod20)ì?í??????

證明首先定義一個C3×C20上的羅馬{3}-控制函數g(vi，j)(0≤i≤2，0≤j≤19)，

函數g也可以表示為下面更直觀的形式：

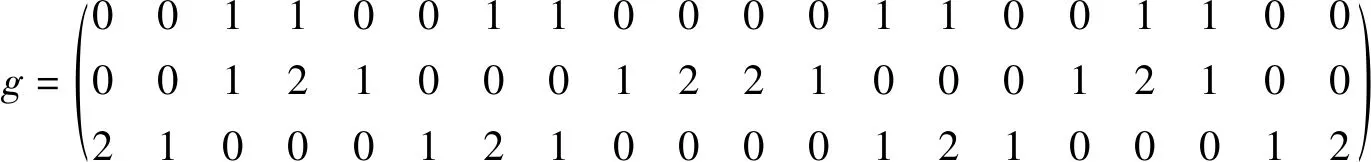
情況1當m≡0，1，7，14(mod 20)時，構造C3×Cm上的羅馬{3}-控制函數為f(vi，j)=g(vi，j mod 20)，圖2顯示的是C3×C21上的f．

圖2 C3×C21上的fFig.2 f on C3×C21

此時，f的權重為

w(f)=m20×36=9m5; m≡0(mod20)m-120×36+2=9m+15=9m5; m≡1(mod20)m-720×36+13=9m+25=9m5; m≡7(mod20)m-1420×36+26=9m+45=9m5; m≡14(mod20)ì?í??????????????

情況2當m≡2，3，4，5(mod 20)時，構造C3×Cm上的羅馬{3}-控制函數f如下：

圖3顯示的是C3×C24上按照上式定義的羅馬{3}-控制函數f．

圖3 C3×C24上的fFig.3 f on C3×C24

此時，f的權重為

w(f)=m-220×36+4=9m+25=9m5;m≡2(mod20)m-320×36+6=9m+35=9m5;m≡3(mod20)m-420×36+8=9m+45=9m5;m≡4(mod20)m-520×36+10=9m+55=9m5+1;m≡5(mod20)ì?í????????????????

情況3當m≡8，9，10，15，19(mod 20)時，構造C3×Cm上的羅馬{3}-控制函數f如下：

圖4(a)顯示的是C3×C10上按照上式定義的羅馬{3}-控制函數f．

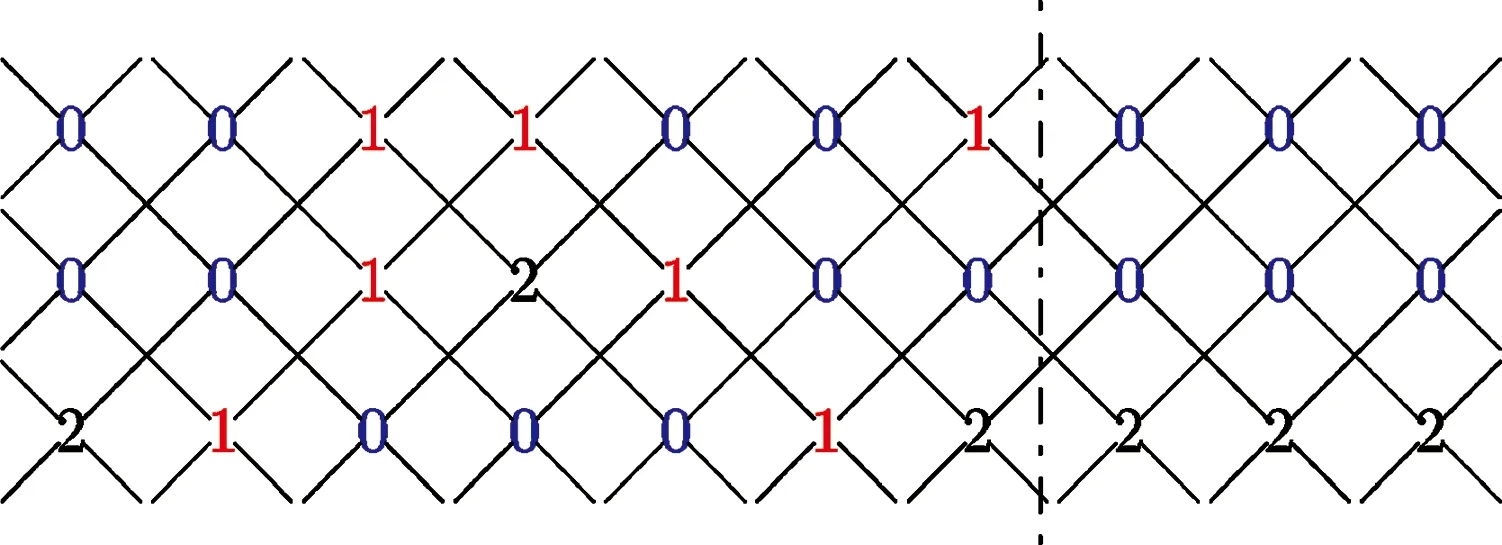
(a)C3×C10上的f

此時，f的權重為

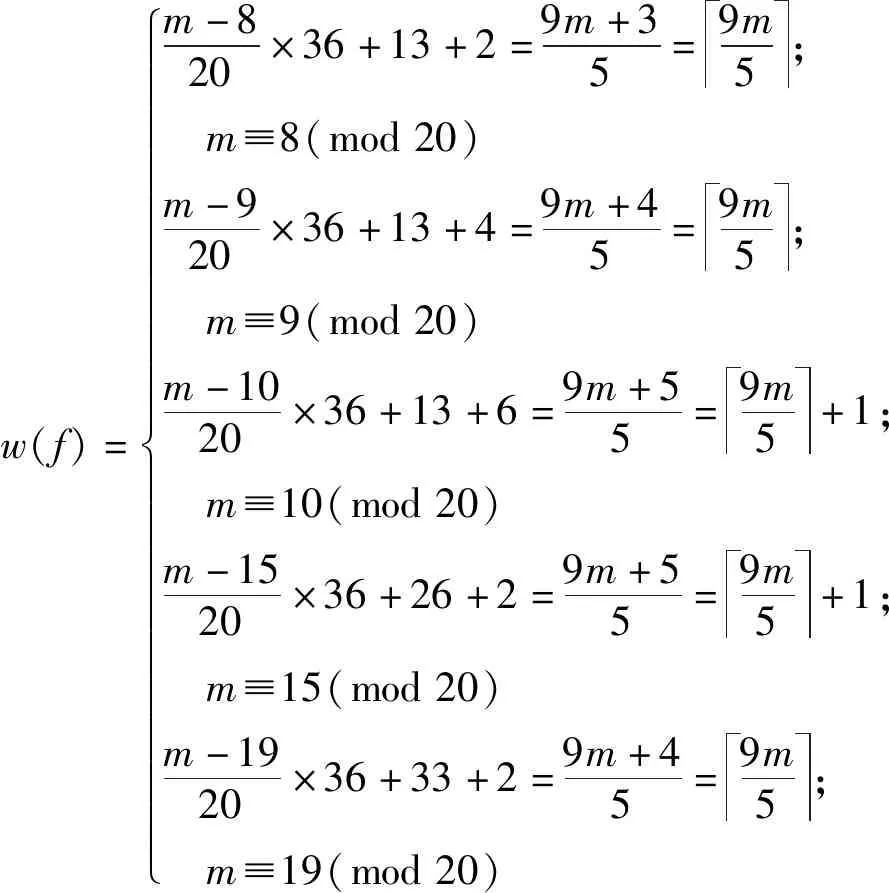
w(f)=m-820×36+13+2=9m+35=9m5; m≡8(mod20)m-920×36+13+4=9m+45=9m5; m≡9(mod20)m-1020×36+13+6=9m+55=9m5+1; m≡10(mod20)m-1520×36+26+2=9m+55=9m5+1; m≡15(mod20)m-1920×36+33+2=9m+45=9m5; m≡19(mod20)ì?í????????????????????

情況4當m≡6，12，13，16，17(mod 20)時，構造C3×Cm上的羅馬{3}-控制函數f如下：

圖4(b)顯示的是C3×C16上按照上式定義的羅馬{3}-控制函數f．此時，f的權重為

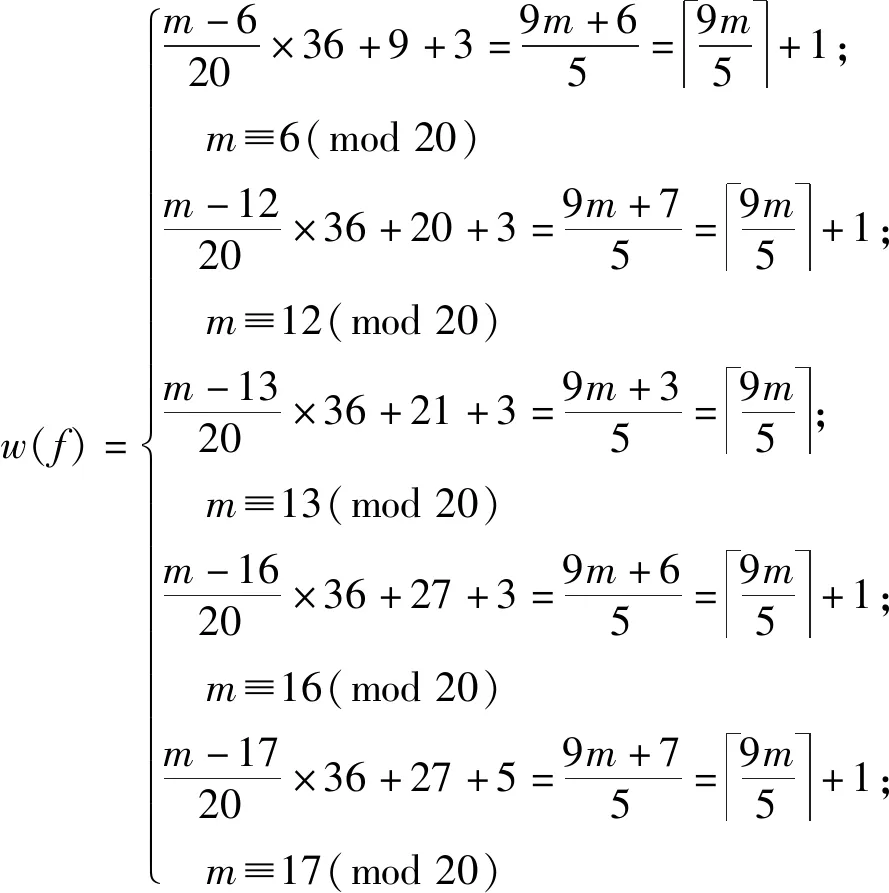
w(f)=m-620×36+9+3=9m+65=9m5+1; m≡6(mod20)m-1220×36+20+3=9m+75=9m5+1; m≡12(mod20)m-1320×36+21+3=9m+35=9m5; m≡13(mod20)m-1620×36+27+3=9m+65=9m5+1; m≡16(mod20)m-1720×36+27+5=9m+75=9m5+1; m≡17(mod20)ì?í????????????????????

情況5當m≡11，18(mod 20)時，構造C3×Cm上的羅馬{3}-控制函數f如下：

圖5顯示的是C3×C18上按照上式定義的羅馬{3}-控制函數f．

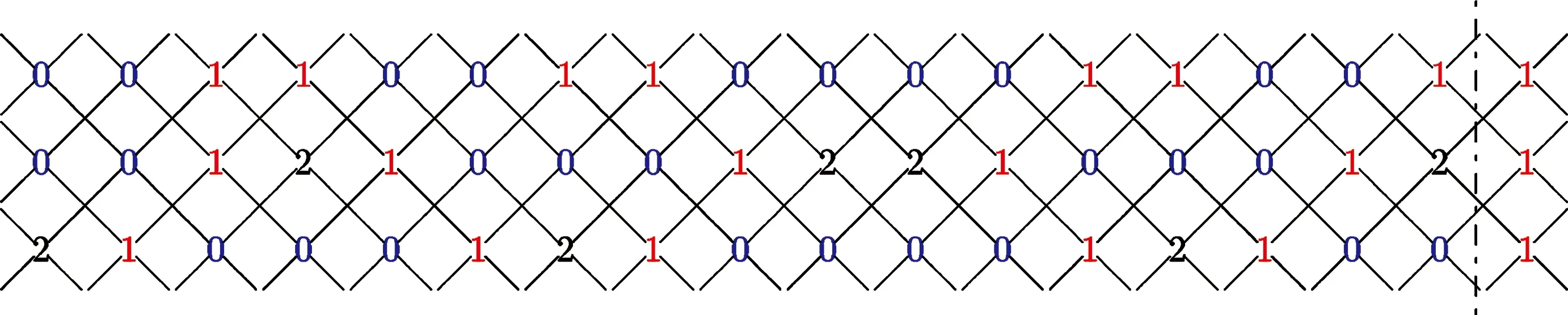
圖5 C3×C18上的fFig.5 f on C3×C18

此時，f的權重為

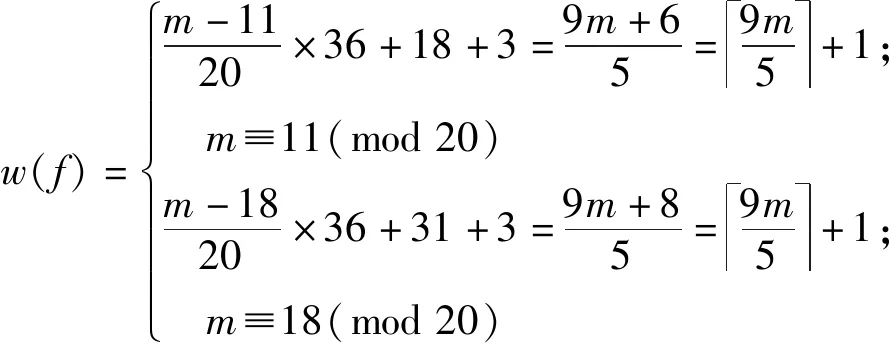
w(f)=m-1120×36+18+3=9m+65=9m5+1; m≡11(mod20)m-1820×36+31+3=9m+85=9m5+1; m≡18(mod20)ì?í????????

由情況1～5可知

γ{R3}(C3×Cm)≤w(f)=

9m5;m≡0,1,2,3,4,7,8,9,13,14,19(mod20)9m5+1;m≡5,6,10,11,12,15,16,17,18(mod20)ì?í????????

□

定理3對于任意的正整數m≥4，G=C4×Cm的羅馬{3}-控制數上界為

γ{R3}(C4×Cm)≤13m5; m≡0,1,2,4(mod5),m≥513m5+1; m≡3(mod5)或m=4ì?í????????

證明

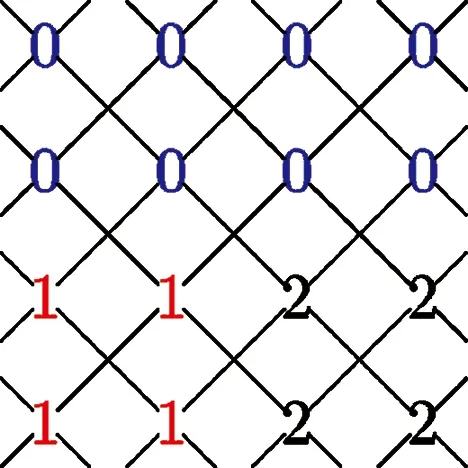
(a)C4×C4上的f

情況2當m≥5且m≠7時，先定義函數g(vi，j)(0≤i≤3，0≤j≤4)(如圖7中前5列)：

然后，構造C4×Cm(m≡0，1，2，3，4(mod 5))上的羅馬{3}-控制函數f如下：

圖7顯示的是C4×C17上按照上式定義的羅馬{3}-控制函數f．

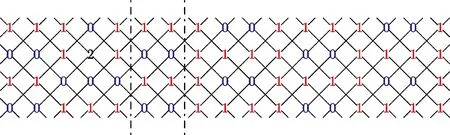
圖7 C4×C17上的fFig.7 f on C4×C17

此時，f的權重為

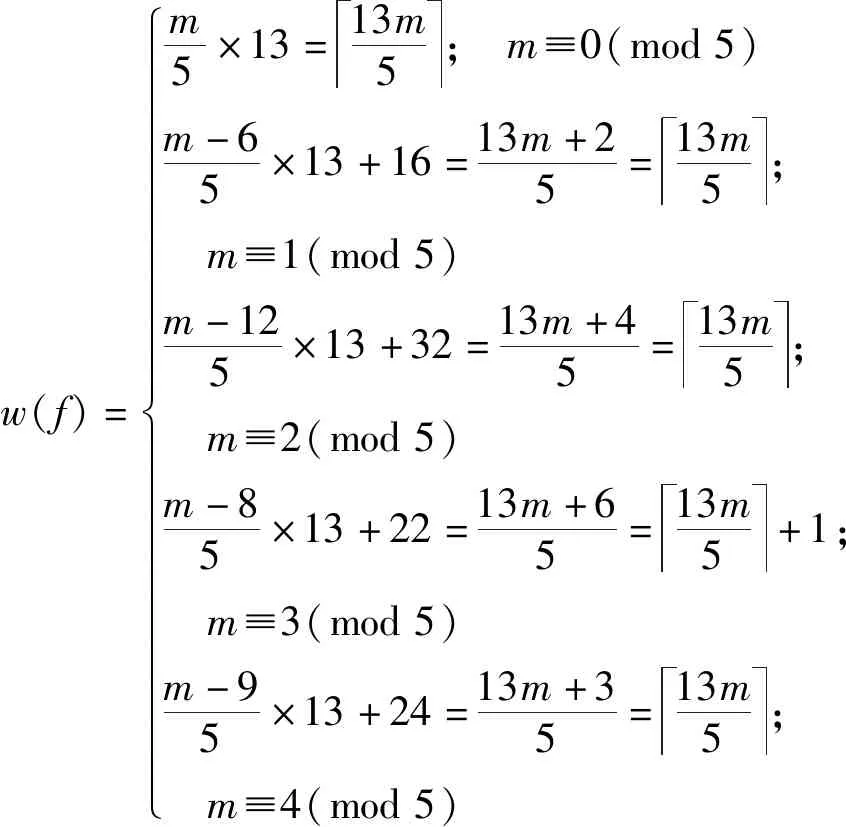
w(f)=m5×13=13m5; m≡0(mod5)m-65×13+16=13m+25=13m5; m≡1(mod5)m-125×13+32=13m+45=13m5; m≡2(mod5)m-85×13+22=13m+65=13m5+1; m≡3(mod5)m-95×13+24=13m+35=13m5; m≡4(mod5)ì?í??????????????????

由情況1和2可知

γ{R3}(C4×Cm)≤w(f)=

13m5; m≡0,1,2,4(mod5),m≥513m5+1; m≡3(mod5)或m=4ì?í????????

□

證明由于圈與圈克羅內克乘積圖具有對稱性，僅給出n(mod 5)≤m(mod 5)的情況．

情況1當n≡0(mod 5)時，先定義函數g(vi，j)(0≤i≤4，0≤j≤4)如下：

然后，構造Cn×Cm(m≡0，1，2，3，4(mod 5))上的羅馬{3}-控制函數f：

圖8顯示的是C5×C7和C5×C8上按照上式定義的羅馬{3}-控制函數f．Cn×Cm中每增加5行或5列就增加一個按照函數g定義的循環塊．

此時，f的權重為

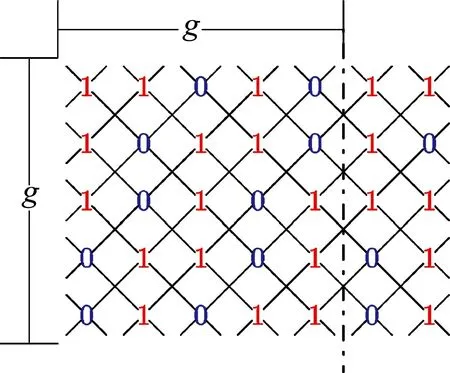
(a)C5×C7上的f

情況2當n≡1(mod 5)時，先定義3個函數g1(vi，j)、g2(vi，j)、g3(vi，j)(0≤i≤4，0≤j≤4)如下：

然后，構造Cn×Cm(m≡1，2，3，4(mod 5))上的羅馬{3}-控制函數f：

圖9顯示的是C11×Cm(m=6，7，8，9)上按照上式定義的羅馬{3}-控制函數f．

此時，f的權重為

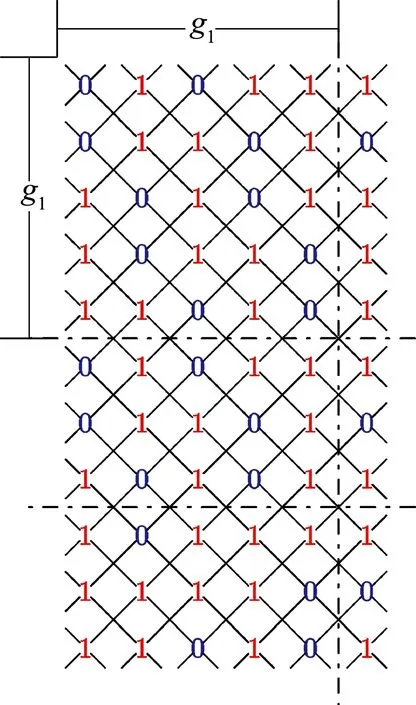
(a)C11×C6上的f

情況3當n≡2(mod 5)時，構造Cn×Cm(m≡2，3，4(mod 5))上的羅馬{3}-控制函數f如下：

其中，g1、g3如情況2中的定義．圖10顯示的是C7×C7、C7×C9和C12×C13上按上式定義的羅馬{3}-控制函數f．

此時，f的權重為

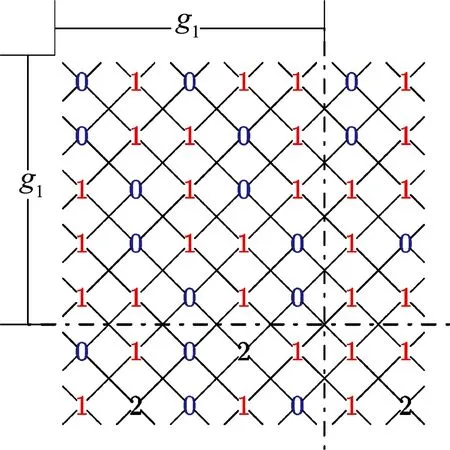
(a)C7×C7上的f

情況4當n≡3(mod 5)時，先定義函數g4(vi，j)(0≤i≤4，0≤j≤4)如下：

然后，構造Cn×Cm(m≡3，4(mod 5))上的羅馬{3}-控制函數f：

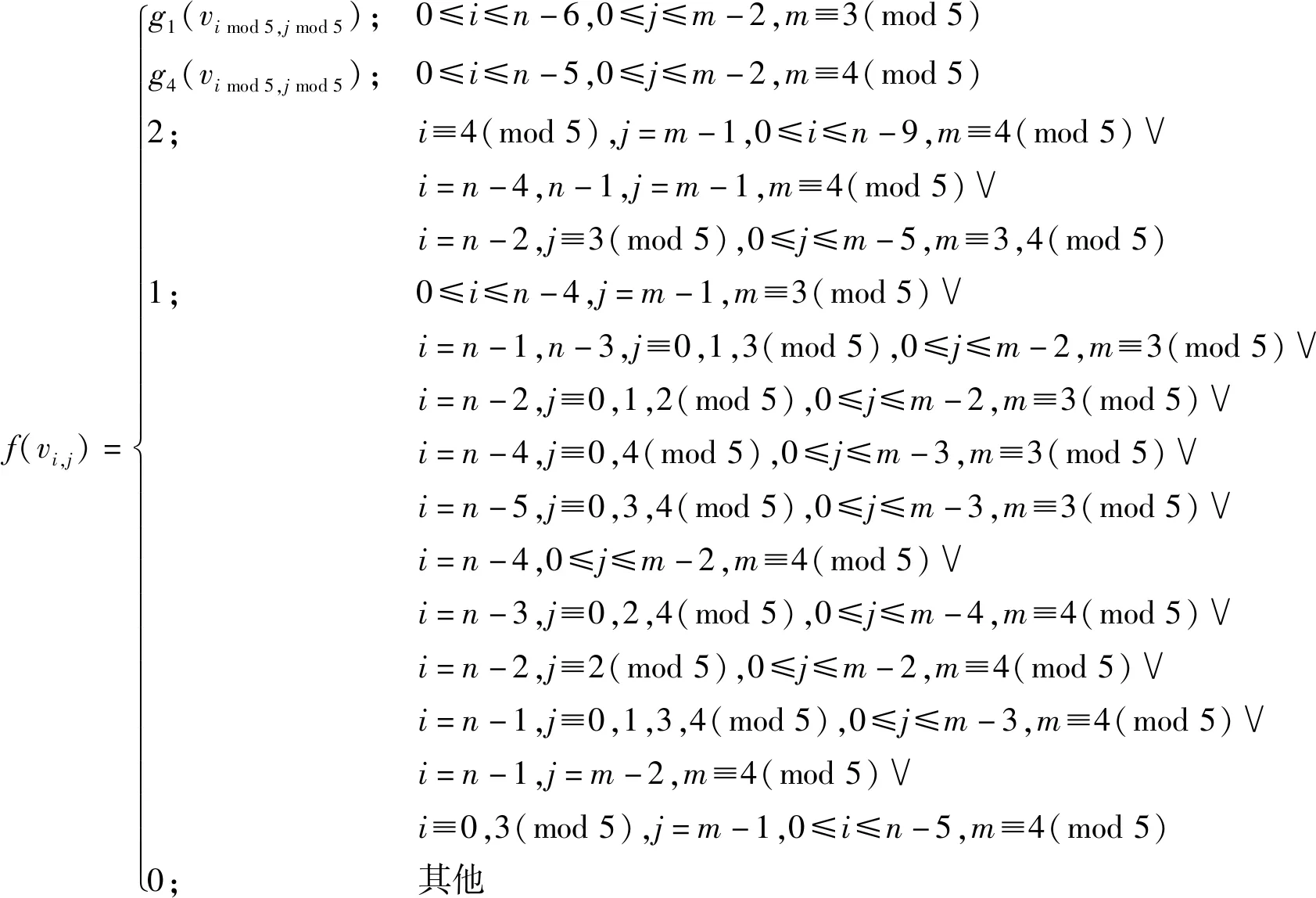
其中，函數g1如情況2中的定義．圖11(a)、(b)顯示了C13×C8和C13×C9上按照上式定義的羅馬{3}-控制函數f．

此時，f的權重為

情況5當n≡4(mod 5)時，先定義函數g5(vi，j)(0≤i≤4，0≤j≤4)如下：

然后，構造Cn×Cm(m≡4(mod 5))上的羅馬{3}-控制函數f：

圖11(c)顯示的是C9×C9上按照上式定義的羅馬{3}-控制函數f．

此時，f的權重為

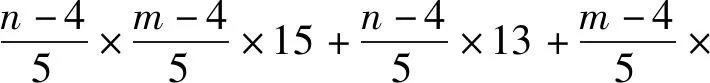
14+11=

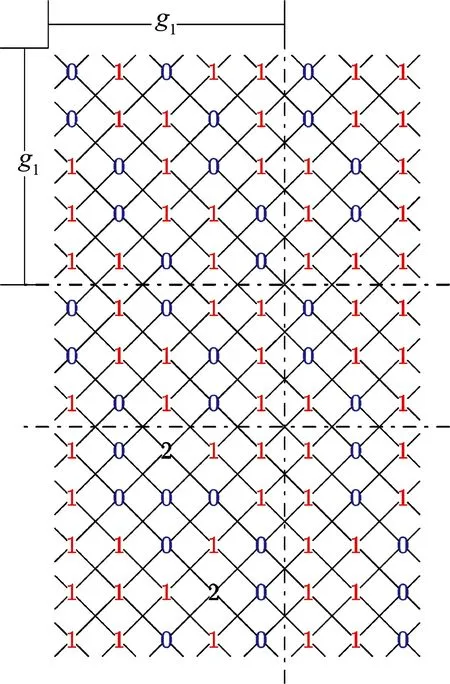
(a)C13×C8上的f

□

由推論1和定理2～4，可以得到

定理5對于任意的正整數m，n≥3，G=Cn×Cm的羅馬{3}-控制數的界為

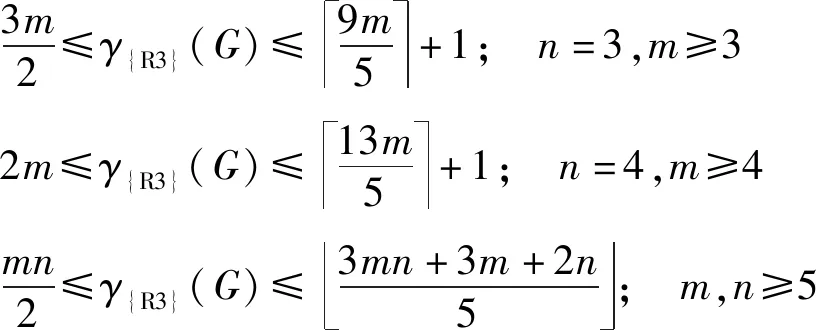
3m2≤γ{R3}(G)≤9m5+1; n=3,m≥32m≤γ{R3}(G)≤13m5+1; n=4,m≥4mn2≤γ{R3}(G)≤3mn+3m+2n5; m,n≥5

3 結 語

本文給出了圈與圈克羅內克乘積圖的羅馬{3}-控制數的界．通過構造圈與圈克羅內克乘積圖的羅馬{3}-控制函數，得到了羅馬{3}-控制數的上界．結合前人給出的一般圖的羅馬{3}-控制數的下界，得到圈與圈克羅內克乘積圖羅馬{3}-控制數的下界．