聲學黑洞能量匯聚效應及阻尼耗能機理研究*

鮑岳 劉獻棟 梁浩鳴 單穎春 何田

（北京航空航天大學，北京 100191）

主題詞：聲學黑洞 寬頻 功率流 波數域 阻尼

1 前言

振動噪聲是影響汽車乘坐舒適性的重要問題之一，目前采用的減振降噪方法往往會造成整車質量增加，開發兼具輕量化和高效減振性能的結構需要新理論的引入。聲學黑洞（Acoustic Black Hole，ABH）具有輕量化、便于集成及可設計性強等特性，且可以高效實現能量匯聚，是一種很有前景的被動降噪技術。

聲學黑洞效應由Pekeris提出，他發現在非均勻層狀流體介質中不存在反射波，其聲速隨剖面深度的增加而衰減為零。Mironov證明了在厚度呈一定冪指數規律減小的楔形梁中彎曲波將不會發生反射，理論上波速將降低為0。Krylov隨后通過幾何聲學方法推導了聲波在這種結構中的程函方程與振幅表達式，并提出了實現聲學黑洞效應所需要的條件與結構假設。理論證明，該結構厚度需要降至零才滿足聲學黑洞效應，但實際上并不存在這種結構，現實中聲學黑洞結構都保留一定的殘余厚度，而極小的殘余厚度都會使得結構中的彎曲波出現大量反射。Krylov 通過在聲學黑洞部位貼附少量阻尼，有效減少了彎曲波的反射，實現了聲學黑洞結構的能量匯聚效應。

從表可以看出，P值均為0.25，大于顯著性水平0.05，卡方對應的P值具有統計顯著性，通過顯著水平為95%的顯著性檢驗。卡方與自由度之比為1.622，小于2。同時，GFI接近于1，RMSEA小于0.05，以上幾個指標均滿足模型檢驗與擬合優度的要求，說明模型擬合效果較好。

常見的聲學黑洞包括一維聲學黑洞梁結構與二維聲學黑洞板結構。目前，聲學黑洞的主要研究方法包括傳遞矩陣法、假設模態法、幾何聲學法與有限元法。Li等通過傳遞矩陣法研究了聲學黑洞梁的能量匯聚現象，并分析了結構參數對彎曲波能量匯聚的影響。Ma等建立了聲學黑洞的半解析動力學模型，分析了阻尼對二維聲學黑洞結構的減振效果。Huang等通過幾何聲學法得出了彎曲波在不同尺寸聲學黑洞中的傳遞軌跡，并研究了彎曲波發生能量匯聚的集中區域，該方法為阻尼的貼附位置提供了參考。Conlon等通過有限元與邊界元法研究了聲學黑洞陣列結構對薄板振動及聲輻射的改善作用，并討論了通過阻尼布置來優化聲學黑洞的減振效果。

本文通過有限元仿真，利用振動功率流法探討二維聲學黑洞中彎曲波的能量分布，并通過波數域方法探究阻尼與黑洞結構的耦合減振機理，對比內嵌單聲學黑洞板結構與內嵌黑洞陣列板結構對于能量匯聚、阻尼耗能與結構輻射的不同效果。

2 理論與模型

2.1 聲學黑洞理論

為了計算薄板模型的自由場聲輻射，在原有薄板模型外層建立聲學空腔模型與笛卡爾型理想匹配層（Perfectly Matched Layers，PML），如圖2 所示。激勵和邊界條件與前文相同，空氣網格采用四面體單元，網格尺寸為聲波最小波長的1/5，同時PML 內部劃分8 層以確保吸收外場輻射。最后，采用有限元軟件COMSOL計算沿薄板垂直方向距離結構300 mm處的平均輻射聲壓。

式中，()為抗彎強度；為結構撓度；為材料密度；()為薄板厚度函數；為材料泊松比；為時間變量；、分別為板的橫向與縱向尺寸。

2)義棠礦太原組灰巖樣品孔隙分形維數與基質孔隙度表現出正相關的關系，而與孔容表現出負相關的關系，分形維數值為2.671 2～2.843 8，介于煤層與砂巖儲層之間，與頁巖儲層分形維數值相近。

根據幾何聲學假設，板內傳播的彎曲波振幅可表示為：

式中，()為彎曲波幅值；()為彎曲波的累計相位，表示為：

式中，為二維均勻薄板的擬縱波波數；()為彎曲波的光程；為彎曲波波數。

設為常數，當薄板結構厚度()呈指數函數變化，即

綜上所述，電子胃鏡檢查是診斷鉤蟲性十二指腸炎綜合征的有效且可靠的診斷方法，做到早發現、早診斷、早治療。

式中，為與聲學黑洞中心點的距離。

通過有限元模擬計算不同激勵頻率下薄板各位置的振動速度響應，得到薄板中心正方形區域（200 mm×200 mm）與薄板均勻部分截面的平均振動速度，不同薄板振動位置的平均振動速度對比數據如圖3、圖4 所示。從圖3與圖4中可以看出，由于嵌有聲學黑洞的薄板剛度較小，中心黑洞區域相比均勻薄板中心區域的振動速度高，貼附阻尼后，當激勵頻率高于黑洞截止頻率時，嵌有聲學黑洞薄板的振動速度得到明顯改善；板均勻部分處，貼附阻尼的ABH 薄板平均振動速度也低于普通薄板。這說明聲學黑洞將板內振動能量匯聚并通過阻尼耗散，并且聲學黑洞結構與阻尼的耦合作用明顯，但阻尼對平板振動幾乎沒有改善效果。

2.2 內嵌聲學黑洞結構的薄板模型

本文主要研究以下幾種薄板結構：均勻平板、背面貼附圓形阻尼的均勻平板、內嵌單聲學黑洞結構的平板、背面貼附圓形阻尼的單聲學黑洞板、內嵌聲學黑洞結構陣列的薄板和背面貼附多個圓形阻尼的聲學黑洞結構陣列薄板。所有薄板結構尺寸均為800 mm×800 mm×2 mm，圓形阻尼層的厚度為0.8 mm，半徑為30 mm。聲學黑洞的厚度函數滿足：

且指數≥2時，彎曲波累計相位趨于無窮大，理論上彎曲波無法傳播至黑洞邊界，這樣就形成了彎曲波的能量匯聚效應。但現實中聲學黑洞結構都存在一定的殘余厚度，同時，聲學黑洞的匯聚效應需要滿足板內的彎曲波波長小于黑洞直徑，故存在聲學黑洞效應的下限頻率：

不同薄板結構與聲學黑洞尺寸如圖1所示。

圖1 結構模型

薄板模型采用C3D20R二次實體單元建模，為了保證計算精度，每個單元尺寸須小于彎曲波波長的1/10。內嵌聲學黑洞鋼板與阻尼層采用綁定約束，鋼板與阻尼層的材料參數如表1 所示。模型四周邊界均采用固支約束。各模型中，使用幅值為1 N的正弦集中力激勵薄板的相同位置（見圖1），激勵頻率范圍為10～6 000 Hz。使用有限元軟件Abaqus對上述模型進行仿真計算。

相關性研究證實,去甲腎上腺素、γ-氨基丁酸及5-羥色胺、谷氨酸等參與了帕金森病癡呆患者疾病的發生及發展,興奮性神經遞質在腦中谷氨酸含量最高,具有生理功能,屬于調節劑,可參與腦部智能活動及認知活動,臨床研究發現,若能量不足,可導致患者減少谷氨酸攝入量,可增加谷氨酸釋放量,升高的谷氨酸可導致患者部分細胞膜發生去極化并導致患者喪失鈣離子穩態[3],可增加NMDA受體內流并產生背景噪音,可對突觸信號檢測造成影響,若鈣離子水平持續增加可導致患者出現神經變性,可誘導患者下降認知功能,可表現出退行性癡呆臨床癥狀[4]。

表1 鋼板與阻尼的材料參數

對于變厚度薄板結構，彎曲波波動方程為：

②州城即山陰縣城，秦始皇改大越為山陰縣，屬會稽郡。南朝宋在會稽郡置東揚州，齊、梁、陳因裘，州治設在山陰縣城，故山陰城也稱州城。

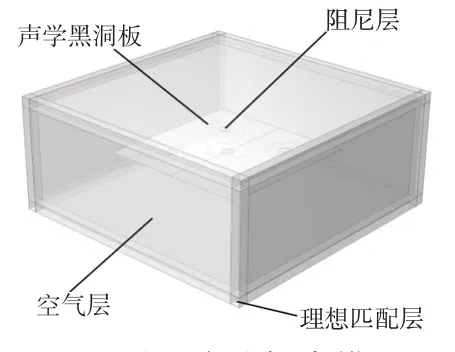
圖2 板-聲腔耦合模型

3 振動功率流與波數域分析

3.1 振動功率流分析

聲學黑洞對穩態振動下的彎曲波能量匯聚作用明顯，在瞬態激勵下也能觀察到相似現象。對瞬態激勵下聲學黑洞模型進行時域分析，施加1 000 Hz正弦信號激勵，載荷時長為7 ms，所有時間段內聲學黑洞區域的時域平均振動速度如圖10所示。由圖10可以看出，貼附阻尼后聲學黑洞的振動速度明顯降低。3 個截面處聲學黑洞薄板不同區域振動速度與時間的關系如圖11所示，與前文頻域分析結果一致，彎曲波能量最大的區域位于聲學黑洞中央區域，但并非圓心位置，而是略微偏離中心，與激勵方向的位置相反。可以看出，聲學黑洞對于聲波的匯聚與“凸透鏡”對于光波的匯聚作用非常相似。

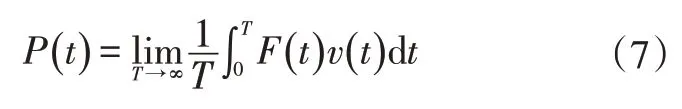
水是生命之源、生態之基。習近平主席指出“綠水青山就是金山銀山”。當前水資源面臨資源短缺，地下水儲量不足，導致地表水逐漸成為飲用水水源。因地表水易受污染，水源保護尤其重要。要大力保障飲水安全、供水安全、生態安全，著力解決人民群眾最關心、最直接、最現實的水資源問題。

通過傅里葉變換可以得到對應頻域的復功率流()的表達式：

（1）強調團隊協作，營造和諧氛圍，保證職責分明而不影響親和力，確保全體員工均能全身心投入。首先，應形成良好的合作意識，保證日常住宿與飲食，并提高自身責任心，同時，在不影響日常工作的基礎上，豐富業余生活，以此進一步提高凝聚力。

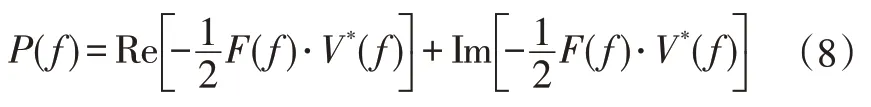
式中，()為結構上某一點外力的傅里葉變換結果；()為該點速度傅里葉變換結果的共軛復數。

復功率流包括有功功率與無功功率。在簡諧激勵條件下，有功功率流等于時間平均功率流，表示單位周期內的平均能量。

3.2 波數域分析

時間域可以通過一維傅里葉變換變換到頻率域，同樣地，空間域的振動能量分布也可以通過二維傅里葉變換變換到波數域。本文采用振動速度來描述薄板的振動能量，變換公式為：

式中，k=2πξ、k=2πξ分別為、方向的波數，ξ、ξ分別為、方向的空間頻率；(k,k,f)為經過二維傅里葉變換后波數域上的頻譜幅值；()為在頻率處的振動速度幅值。

波數域分析能夠清晰反映彎曲波在傳播過程中波長的變化情況，有助于揭示聲學黑洞結構的能量匯聚機理及阻尼耦合效應。

式中，()、()分別為結構上某一點的瞬時外力與瞬時速度；為觀測時長。

4 數值計算結果

4.1 內嵌單聲學黑洞薄板的能量匯聚效應分析

式中，為聲學黑洞的半徑；為薄板均勻部分厚度；為材料的彈性模量；為材料密度；為材料的泊松比。

輪對存放庫體型大，整體運輸較為困難，因此，采用分步制造的方式。制造加工時在制造廠進行焊接、加工和組裝后，分段運輸到現場進行安裝。立柱與地面采用地腳螺栓進行聯接固定，整個輪對存放庫安裝完畢后，進行外觀處理。

圖3 不同薄板結構中心區域的均方根振動速度對比

圖4 不同薄板結構均勻厚度區域的均方根振動速度對比

進一步計算黑洞區域中彎曲波能量功率流分布情況，圖5 所示為施加激勵頻率分別為200 Hz、2 000 Hz、6 000 Hz 下黑洞區域的二維功率流云圖。由圖5 可以看出：在截止頻率以上，在聲學黑洞區域附近功率流矢量發生偏轉，匯聚于黑洞中心的殘余厚度區域附近，且位于聲學黑洞中心區域的功率流能量遠大于黑洞區域外，而低于截止頻率的彎曲波能量不發生匯聚。

圖5 不同激勵頻率下聲學黑洞區域的二維功率流云圖

為了更加直觀地表示彎曲波在薄板中的能量分布，將每個頻率下的功率流能量進行平均，不同薄板在全頻段功率流的平均能量如圖6所示，貼附阻尼的聲學黑洞結構在低頻、中頻和高頻段的能量耗散作用對比結果如圖7 所示。從圖中可以看出：在截止頻率以上，聲學黑洞能量匯聚效應明顯，貼附阻尼后彎曲波能量明顯衰減；在截止頻率范圍以下，振動能量并未出現降低。上述結果說明，只有當激勵頻率高于截止頻率時，聲學黑洞才會發生顯著的能量匯聚及阻尼耦合效應。由此可知：均勻薄板不發生能量匯聚，貼附阻尼層對板內彎曲波能量耗散作用十分有限。

圖6 全頻段（0～6 000 Hz）平板與聲學黑洞結構貼附和不貼附阻尼的平均功率流圖對比

圖7 低、中、高頻激勵下聲學黑洞與聲學黑洞結構貼附阻尼的平均功率流圖對比

將仿真得到的板內振動速度空間分布情況通過二維傅里葉變換得到彎曲波在板內傳播的波數域分布。圖8 所示為全頻段內3 種薄板的波數域能量分布情況，低、中、高頻激勵下的波數域圖像對比結果如圖9 所示。可以看出：施加的載荷頻率越高，薄板內的彎曲波振動波長越短，波數增加；針對高于截止頻率的激勵頻率，相比均勻薄板，內嵌單ABH 薄板的彎曲波波數分布出現低波數向高波數的遷移現象，彎曲波波長壓縮現象明顯；貼附阻尼后，圖像中外圍的高波數能量降低。

圖8 全頻段（0～6 000 Hz）平板與聲學黑洞結構貼附和不貼附阻尼的平均振動速度波數對比

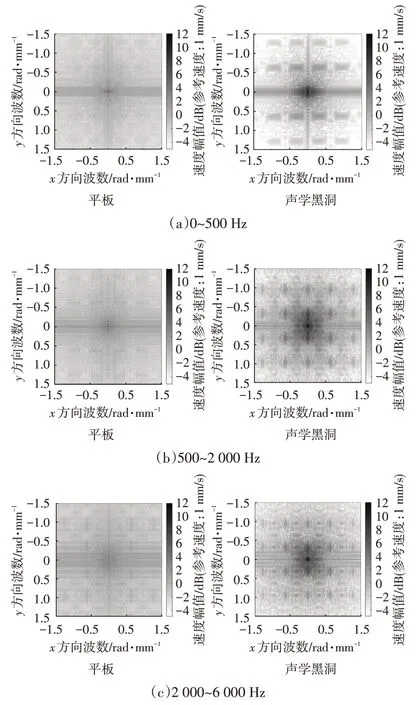
圖9 低、中、高頻激勵下平板與聲學黑洞結構的平均振動速度波數對比

振動功率流分析是一種直觀描述結構在單位面積截面上的能量強度與傳遞方向的方法。時間平均功率流()的表達式為：

圖10 7 ms內聲學黑洞結構貼附和不貼附阻尼的時域平均振動速度分布

圖11 內嵌聲學黑洞結構不同截面處的平均振動速度曲線

4.2 聲學黑洞陣列的能量匯聚效應分析

為了進一步考察薄板內嵌黑洞陣列結構的振動性能，通過仿真計算了內嵌聲學黑洞陣列薄板振動速度，該聲學黑洞陣列結構含有5 個聲學黑洞單元。同時與之前討論的單個聲學黑洞結構進行對比，不同結構的振動速度如圖12 與圖13 所示。其中內嵌ABH 陣列板與內嵌單個ABH 薄板振動速度都高于平板，但陣列板振動速度低于單ABH 板，這是由于多個聲學黑洞分散了板內的振動能量。相比單聲學黑洞，聲學黑洞陣列與阻尼的耦合效應更加明顯；當施加載荷激勵低于聲學黑洞的截止頻率，即在300～500 Hz 范圍內時，貼合阻尼后ABH 陣列板的振動水平有了明顯改善，這與內嵌單聲學黑洞板的現象不同。

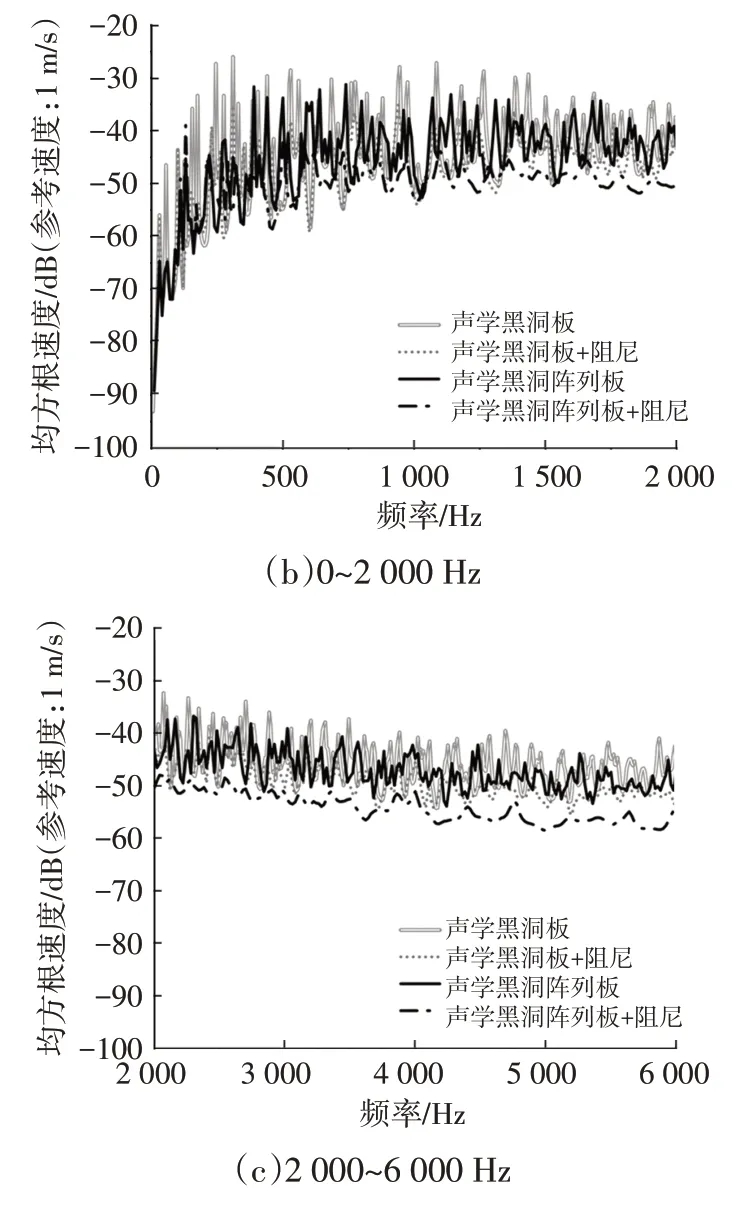
圖12 不同薄板結構中心區域的均方根振動速度對比

圖13 不同薄板結構均勻厚度區域的均方根振動速度對比

聲學黑洞陣列板的平均功率流能量如圖14 所示，相比內嵌單個黑洞，聲學黑洞陣列板結構對振動衰減作用更加明顯。不同頻率段的平均功率流分布如圖15所示，聲學黑洞陣列對于截止頻率內的低頻激勵仍然存在很強的能量匯聚與阻尼耦合效應。

圖14 全頻段（0～6 000 Hz）聲學黑洞與聲學黑洞陣列結構貼附和不貼附阻尼的平均功率流

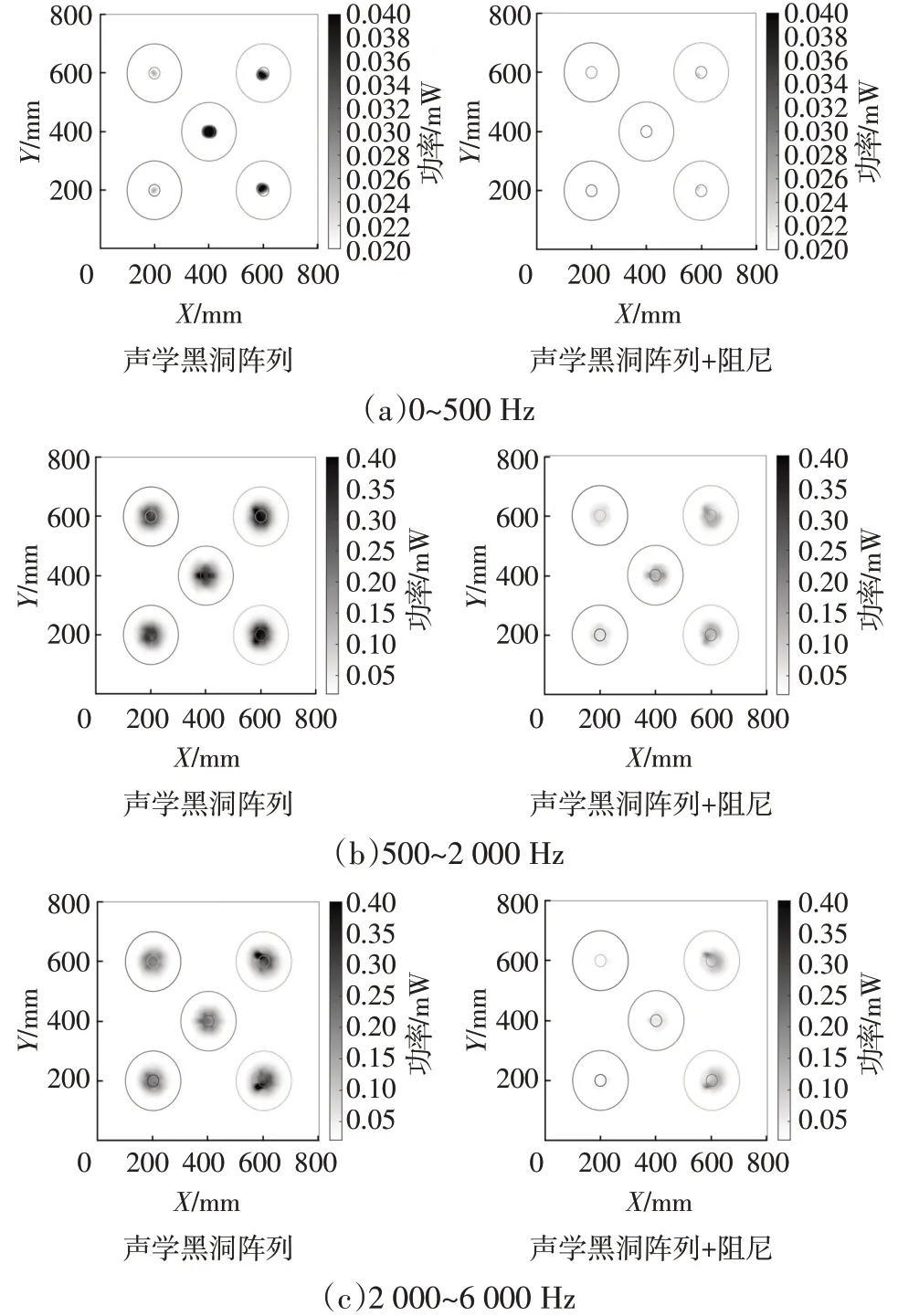
圖15 低、中、高頻激勵下聲學黑洞陣列與聲學黑洞陣列貼附阻尼結構的平均功率流

聲學黑洞陣列板的波數域圖像如圖16 所示，聲學黑洞陣列對高波數能量的衰減作用明顯強于單聲學黑洞薄板。各頻率段振動波數域圖如圖17 所示，低于截止頻率500 Hz 時，阻尼對聲學黑洞陣列板振動能量的減弱效果就已經非常明顯；同時，由于多聲學黑洞結構分散了板內的低波數能量，使得低波數域能量也出現了明顯降低。由此證明，相比于內嵌單個黑洞薄板，聲學黑洞陣列不僅對于全頻段振動能量衰減具有更優效果，同時也能改善因為聲學黑洞截止頻率存在而導致單個聲學黑洞低頻減振效果較差的問題。

式中，l為光伏方陣的斜面長度；θ為光伏方陣的安裝傾斜角度；h為障礙物的高度；β為太陽方位角，均為正值；α為太陽高度角。若建筑中存在方位偏角σ，則需要將公式中的β替換為β+σ進行分別計算，以二者之間的較大值作為方陣間距值。而針對坡屋面1的類型，處于屋面南坡的光伏間距D1因為受到屋面坡度角的影響會導致間距相對較小，屋面北坡的光伏間距D2則會變大，光伏方陣的間距計算圖如圖2所示。

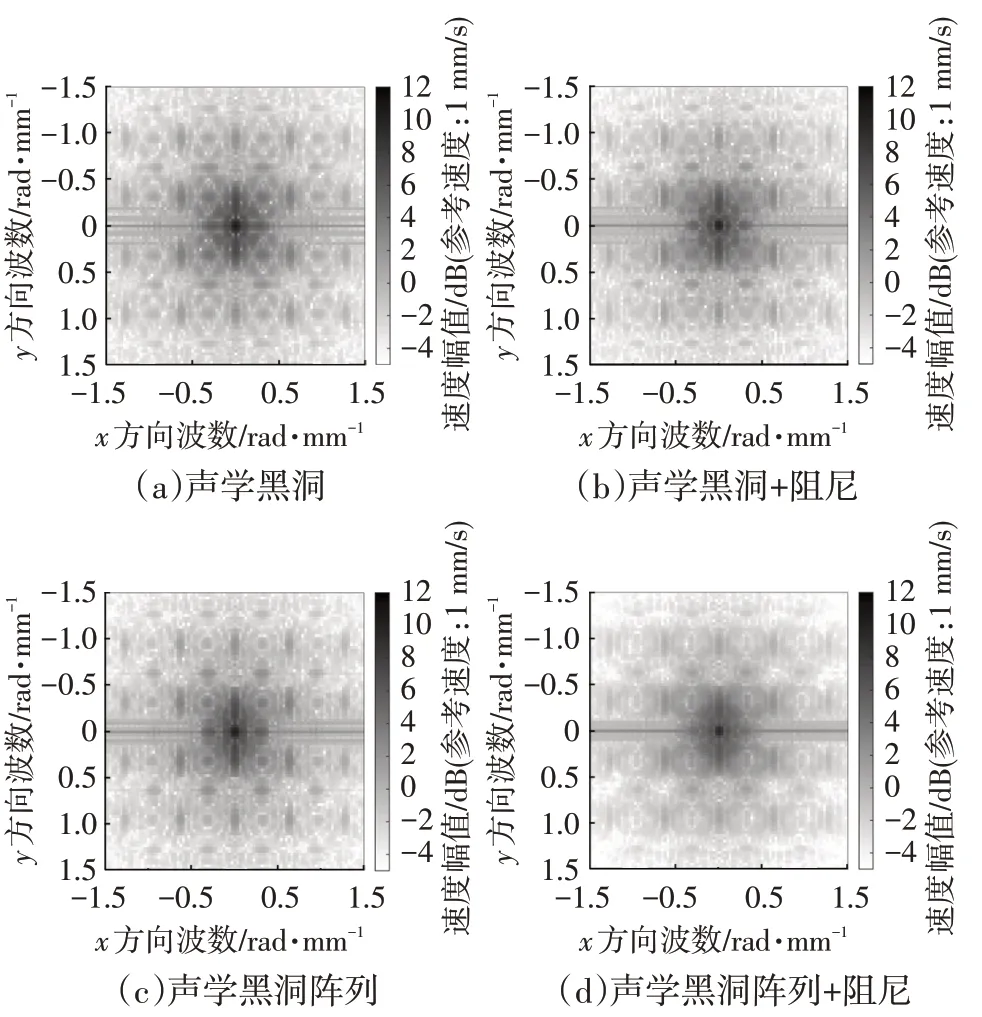
圖16 全頻段（0～6 000 Hz）聲學黑洞與聲學黑洞陣列結構貼附和不貼附阻尼的平均振動速度波數

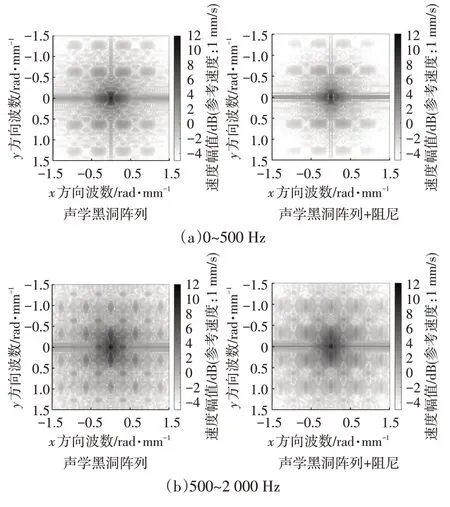
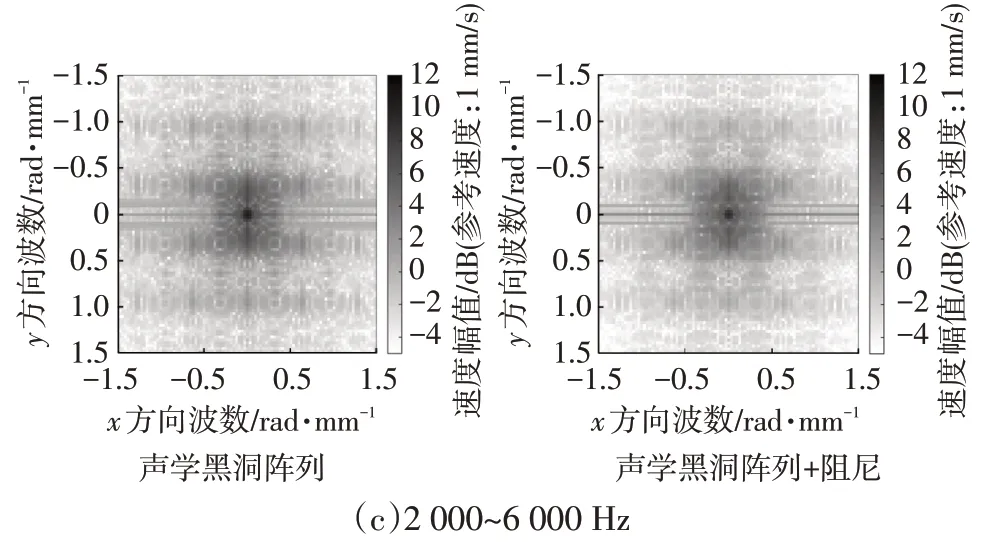
圖17 低、中、高頻激勵下聲學黑洞陣列與聲學黑洞陣列貼附阻尼結構的平均振動速度波數

4.3 聲學黑洞與阻尼耦合機理分析

通過復模態計算可以得到整體系統的模態阻尼損耗因子，清楚地表征薄板結構與阻尼之間的耦合作用。3 種不同薄板結構的模態阻尼損耗因子與頻率的關系如圖17 所示。當激勵頻率高于截止頻率時，板內的彎曲波波長小于黑洞尺寸，彎曲波整體進入黑洞結構，振幅變大，波長被壓縮，此時薄板整體結構與阻尼發生相互作用，在相當寬的頻域內阻尼損耗因子顯著提升；而當激勵頻率低于截止頻率時，彎曲波波長大于聲學黑洞尺寸，此時黑洞結構不再具有能量匯聚效應，但黑洞結構的局部模態與阻尼層之間仍存在強烈的耦合作用，這也可以改善整體結構的模態阻尼。但是，這種阻尼耦合效應只在局部模態頻率下才起作用（圖18 所示為內嵌單聲學黑洞與阻尼耦合的前3 階模態振型），因為單個黑洞結構在低頻的局部模態數量少，所以阻尼對內嵌單聲學黑洞板的低頻振動改善效果有限。而多聲學黑洞陣列的結構具有復雜性，使得黑洞陣列結構在低頻下也具有相當豐富的局部模態數（不同板結構的模態數量與頻率的關系如圖19所示），這一特點詮釋了聲學黑洞陣列板在低頻范圍內也具有很好的減振效果的原因。

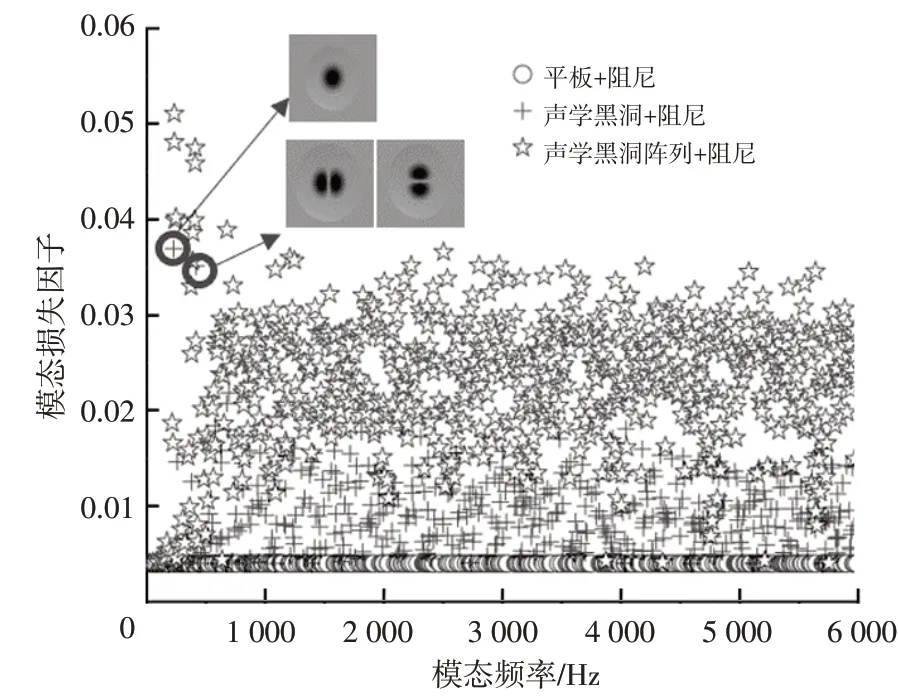
圖18 不同板結構各模態頻率下的模態損失因子及聲學黑洞結構的前4階局部模態振型

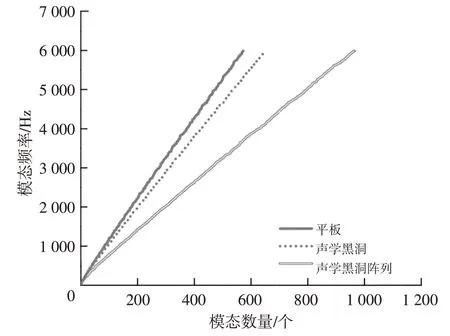
圖19 不同板結構模態數量與模態頻率的關系

同時，由于板內彎曲波波長被壓縮，薄板振動表面與聲場的耦合匹配特性變差，使得薄板的聲輻射降低。不同板結構的輻射聲壓幅值與頻率的關系如圖20 所示，由圖20可以看出，聲學黑洞陣列與阻尼的耦合效應能顯著改善薄板的自由場輻射聲壓，相比普通平板結構，聲學黑洞陣列輻射聲壓最大可降低10 dB。

大電網中虛擬同步發電機慣量支撐與一次調頻功能定位辨析//秦曉輝,蘇麗寧,遲永寧,郭強,徐希望//(9):36

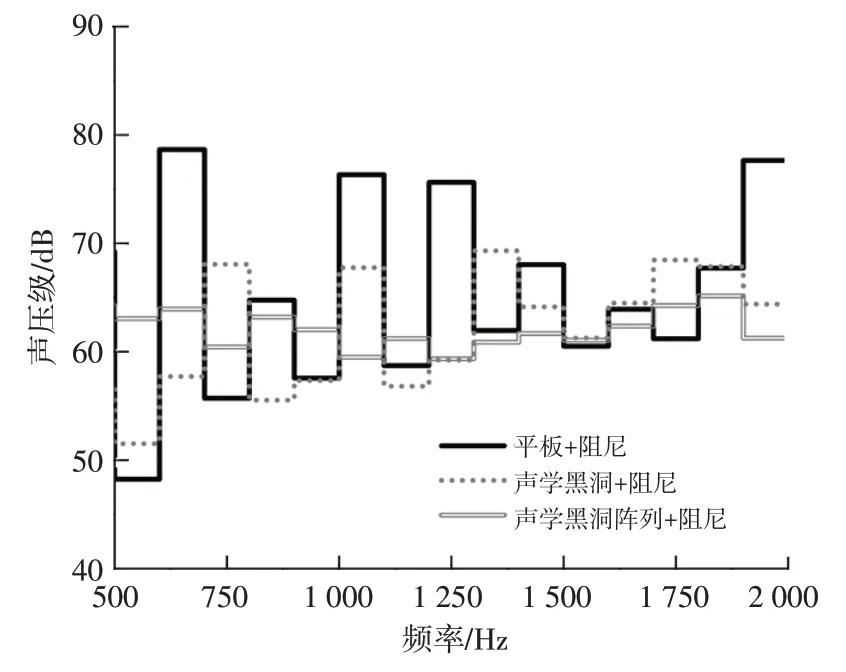
圖20 3種板結構的自由場輻射聲壓值對比

5 試驗驗證

為進一步驗證聲學黑洞的效果，本文加工了聲學黑洞薄板結構，并搭建了試驗平臺進行振動測試，如圖21 所示。按照前文的仿真模型，將帶有單個聲學黑洞的平板結構通過鋁型材固定。盡管實際條件與仿真模型存在些許差異，但不會影響相應的物理現象。同時，引入了阻尼結構來驗證聲學黑洞薄板與阻尼材料的耦合效果。

圖21 試驗裝置

試驗中，信號發生器產生一個頻率為1 000 Hz 的激勵信號，并通過功率放大器驅動電磁激振器激勵薄板，激勵點位置坐標為(670 mm,300 mm,2 mm)。采用加速度傳感器采集振動信號，激勵位置與測量位置分別如圖22 所示，測試原理如圖23 所示。諧波穩定后，對每個點信號進行采樣，采樣時間為5 s。該測試過程采用了重復性驗證方法，排除了偶發因素對結果精度的影響。

圖22 激勵與測量位置

圖23 測試原理

將所采集的信號通過平均可得到聲學黑洞區域的振動加速度，如表2所示。通過對比帶有阻尼的ABH平板結構，可以看出：該方法大幅降低了振動能量，聲學黑洞與阻尼的耦合效果非常明顯。

將建立的三維模型導入comsol軟件中，進行網格劃分，由下圖可以看出，網格劃分較好，進行有限元計算可以得到較為精確的結果；輸入材料的基本參數及設定的外界條件，以天（d）作為計算單位，混凝土溫度測試時間為20d，步長為3d，利用comsol軟件，對在筏板基礎中選取的測點進行模擬計算，與實測數據進行對比分析。

表2 振動加速度測量值

6 結束語

本文應用有限元方法研究了3 種類型薄板（均勻平板、內嵌單個聲學黑洞薄板與內嵌聲學黑洞陣列薄板）的彎曲波能量匯聚效應及振動響應。通過振動功率流與波數域方法研究了彎曲波在聲學黑洞結構中的匯聚現象與波數變化情況，并對低頻及中高頻激勵下的聲學黑洞阻尼耦合機理進行了探究。通過對比這幾種板結構的減振效果及聲輻射大小，證實了貼附阻尼的聲學黑洞結構可以有效改善薄板全頻段的振動與輻射特性。