自動駕駛汽車狀態估計的矩陣加權自適應擴展卡爾曼濾波方法

初宏偉 張穎

（1.長春汽車工業高等專科學校，長春 130013；2.一汽-大眾汽車有限公司，長春 130013）

主題詞：自動駕駛汽車 多傳感器 狀態估計 執行機構故障 卡爾曼濾波

1 前言

自動駕駛感知系統的性能多依賴于其所配置的傳感器硬件方案及相應的汽車狀態估計方法。現有自動駕駛汽車所配置的傳感器包括慣性導航系統（Inertial Navigation System，INS）、全球定位系統（Global Positioning System，GPS）、雷達、光學傳感器等。

以輪胎側向力傳感器為數據源，文獻[5]、文獻[6]采用遞歸最小二乘方法估計側向車速，但因對環境噪聲存在高斯噪聲假設，其跟蹤存在一定時延。文獻[7]通過車速傳感器的信號，采用龍伯格（Luenberger）觀測器法實現了道路坡度的估計。文獻[8]采用擴展卡爾曼濾波器實現了車輪側偏角的估計，但噪聲信息未知導致其狀態估計存在一定偏差。文獻[9]采用無跡卡爾曼濾波器實現了汽車速度估計，并在BMW5上進行了實車試驗，縱、側向速度跟蹤較好。

單一傳感器量測的可靠性相對較差，而采用不同傳感器能夠實現信息融合，從而獲得更為精準的目標信息。目前，歐盟已開始研究雷達與光學傳感器的融合技術。在國內，潘璞利用全球導航衛星系統（Global Navigation Satellite System，GNSS）/INS 組合導航系統設計了自適應卡爾曼濾波方法實現自動駕駛汽車的姿態解算。沈崢楠融合超聲波雷達和可見光攝像頭實現了車位幾何信息識別。彭文正等采用迭代擴展卡爾曼濾波算法融合了慣性測量單元（Inertial Measurement Unit，IMU）、GPS、相機等信息，實現了車輛的定位和速度觀測。劉志在深度學習框架下實現了多源信息的深度融合。綜上所述，多傳感器信息融合技術已然成為當前自動駕駛汽車狀態估計領域的研究熱點。

現有方法鮮有討論汽車故障條件下的狀態和故障聯合估計問題。為此，本文針對自動駕駛汽車提出了一種多傳感器加權融合自適應擴展卡爾曼濾波（Adaptive Extended Kalman Filtering，AEKF）狀態估計方法，通過設計矩陣加權融合方法實現多傳感器信息融合，從而提升感知系統量測精度，以期為自動駕駛汽車的自動泊車、自動避障等應用場景提供參考。

2 自動駕駛汽車運動學模型

自動駕駛汽車運動學模型如圖1所示。根據汽車運動學規律，將上述關系在慣性系下建模為以下運動學方程：

圖1 自動駕駛汽車運動學模型

式中，()為汽車質心在慣性系下的坐標；為車速；為汽車加速度；為汽車行駛航向角；、分別為車輛質心與前、后軸的距離；為汽車行駛方向與車身縱軸的夾角；為汽車前輪轉角。

為便于數字化工程設計，在假設轉向角很小的情況下（≈），將式（1）轉換為離散形式：

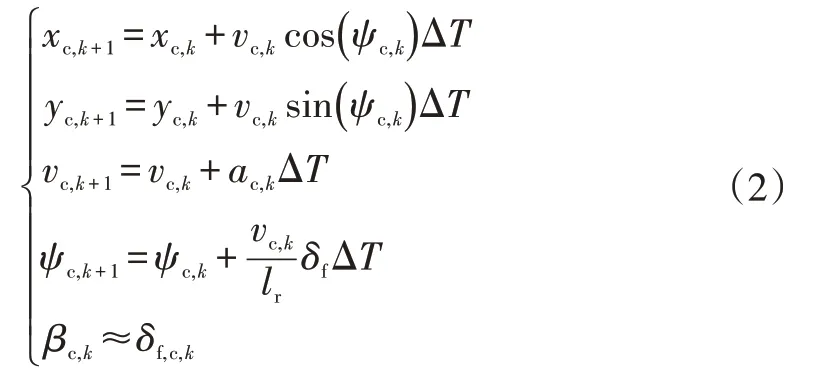
式中，、、、、、、分別為系統時刻、、、、、、的采樣值；Δ為數字測控系統的采樣時間。

本文的目標是針對離散系統式（2），設計多傳感器矩陣加權融合AEKF 估計器，以降低整車成本、提升測控系統的量測精度，實現自動駕駛汽車行駛狀態和執行機構故障的同步估計。

3 汽車行駛狀態估計方法

3.1 自適應擴展卡爾曼濾波

為便于自適應擴展卡爾曼濾波器設計，同時考慮執行機構故障情形，將離散系統式（2）轉化為常規系統描述形式：

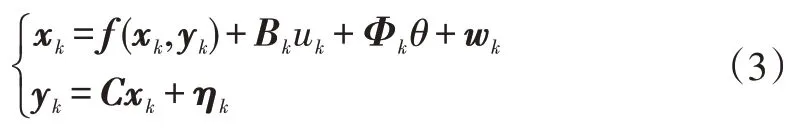
非線性動態方程(x,y)∈R的表達式為：

由于轉換后的系統式（3）存在非線性方程式（4），故采用擴展卡爾曼濾波器設計思路對其進行線性化處理。線性化后的系統為：

至此即完成了系統模型的轉換。本文自適應擴展卡爾曼濾波器設計如下：

a.給定迭代估計的初始條件：

式中，、為系統狀態量初始值；()0、為執行機構故障參數初始值；、為協方差矩陣的初始值；(0)、(0)均為用于求解最優增益矩陣K的輔助矩陣。

b.協方差矩陣一步預測：

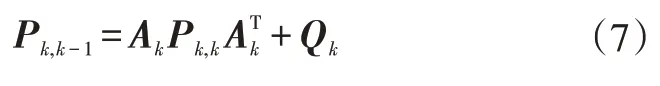
c.狀態估計增益矩陣更新：

式中，Σ=CP+R；R為當前時刻噪聲方差矩陣。

d.故障估計增益矩陣Γ更新：

e.式（9）中對應輔助矩陣H、S、Ω、Λ更新：

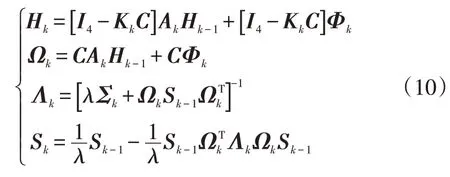
式中，為待設計遺忘因子。

通過式（6）～式（13）的迭代計算，即可通過單個傳感器信息估計得到自動駕駛汽車的狀態和故障信息。關于自適應擴展卡爾曼濾波收斂特性的探討參見文獻[17]。

3.2 多傳感器矩陣加權融合估計方法設計

為解決單一傳感器高精度測控與高成本的矛盾，有效提高自動駕駛汽車整車制造的費效比，通過配置制造成本較低的傳感器，并利用傳感器信息融合技術對汽車狀態進行在線估計成為了工業界的熱點研究方向之一。

設傳感器數量為，通過各傳感器的信號濾波得到的無偏估計x：

式中，表示數學期望。

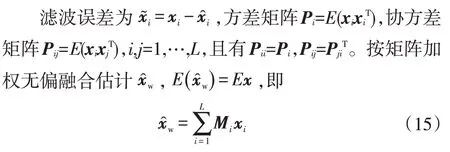
式中，M∈R為加權矩陣。

在線性最小方差意義下，選擇M來極小化估計誤差分量均方和：

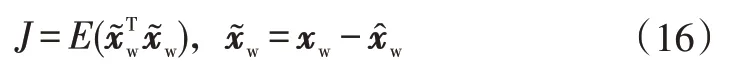
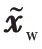
式（16）等價于：

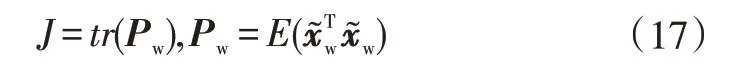
式中，為加權估計的協方差矩陣；()為矩陣的跡。

因局部估計和融合估計均具有無偏性，則以下約束條件成立：

根據式（18）可知：

為了求取各加權矩陣M，設加權矩陣的合成陣為：

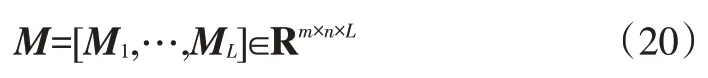
定義未知方差矩陣合成矩陣為：

根據上述定義，性能指標式（17）可寫為：

而約束條件式（18）可轉換為：

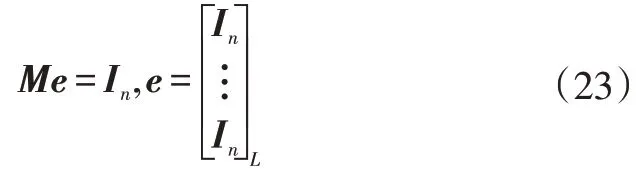
至此，求解矩陣的問題轉換為以式（22）為性能指標的矩陣等式約束極小化問題。采用拉格朗日乘數法，引入輔助函數：

式中，γ=[γ… γ]為拉格朗日乘子向量；e=(0,…,0,1,0,…,0)，其第列元素為1，其他為0。

為極小化性能指標式（24），對輔助函數求的偏導數并令其等于0，即?/?=0，可得：

上式第2項可以寫成如下形式：

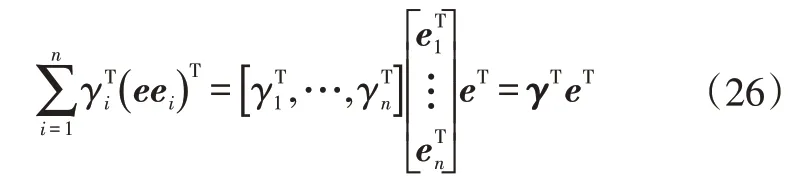
式中，=(,…,γ)=(γ)，該矩陣的第行第列為γ。

根據式（25）和式（26），可得：

輔助函數對求偏導并令其等于0，即?/?=0，則有：

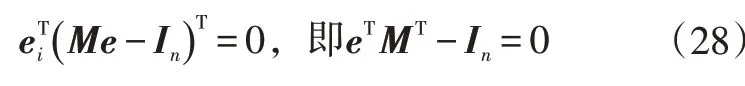
根據上述推導可知：

求解線性方程組式（29），可得：

由式（30）可推知=I，進而可知：

推知：

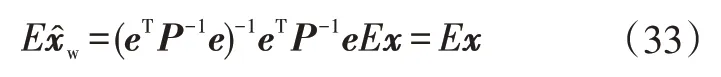
上述推導存在如下關系：

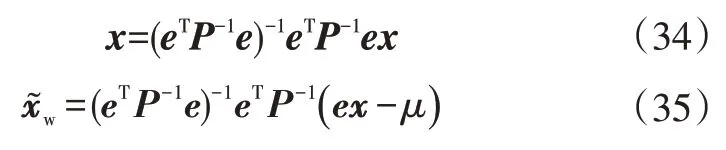
根據協方差矩陣定義可知：

綜合上述推導過程，得到多傳感器矩陣加權融合估計：

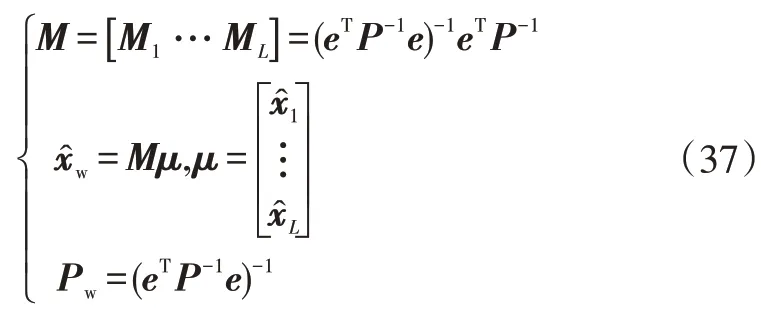
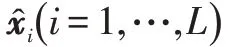
本文所設計方法的整體應用框架如圖2所示。

圖2 本文方法框架

4 仿真分析

4.1 仿真條件設置

為驗證本文所提出的方法的有效性，將本文所提出的AEFK（矩陣加權）方法與單個傳感器的AEKF方法進行對比。驗證方案中，采用了2種不同精度的傳感器對汽車狀態信息進行感知，并設置如表1所示的仿真參數進行方法驗證。

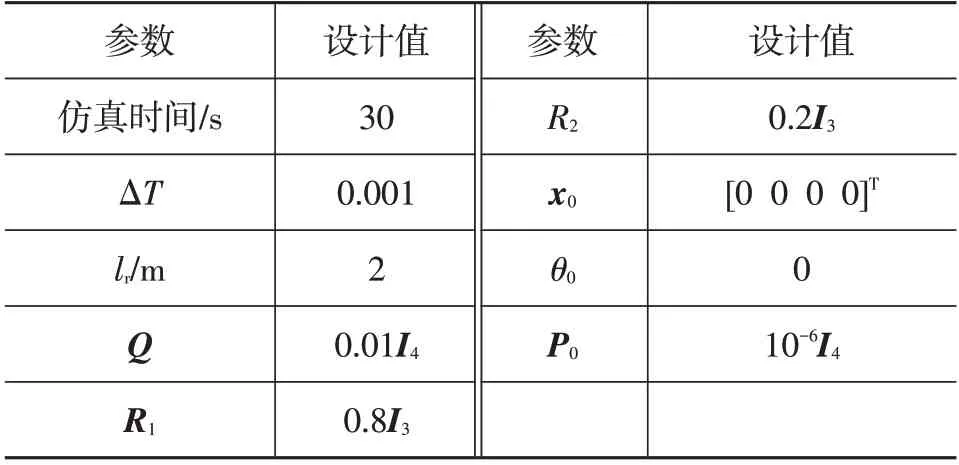
表1 仿真參數

4.2 仿真結果及分析

利用表1 中所設計的仿真參數，以MATLAB 2018b為仿真平臺搭建仿真模型，設置了3種仿真情形：

a.采用低精度傳感器1（=0.8）進行狀態信息采集，并利用3.1 節的AEKF 方法進行狀態和故障系數估計，記為AEKF（傳感器1）；

b.采用高精度傳感器2（=0.2）進行狀態信息采集，并利用3.1 節的AEKF 方法進行狀態和故障系數估計，記為AEKF（傳感器2）；

c.基于情形a 和情形b 得到的估計結果，利用3.2節的多傳感器矩陣加權融合方法進行狀態和故障估計，記為AEKF（矩陣加權）。

根據上述仿真情形和表1的仿真參數設置，得到仿真結果如圖3～圖7所示。

圖3 汽車位置估計結果

圖4 汽車行駛航向角估計結果

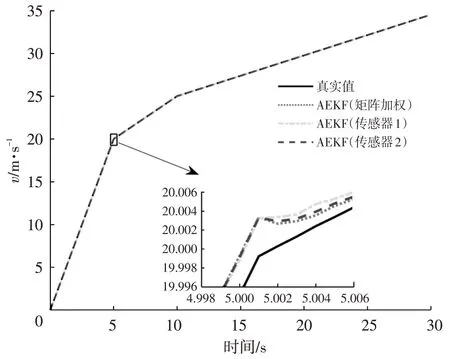
圖5 汽車速度估計結果

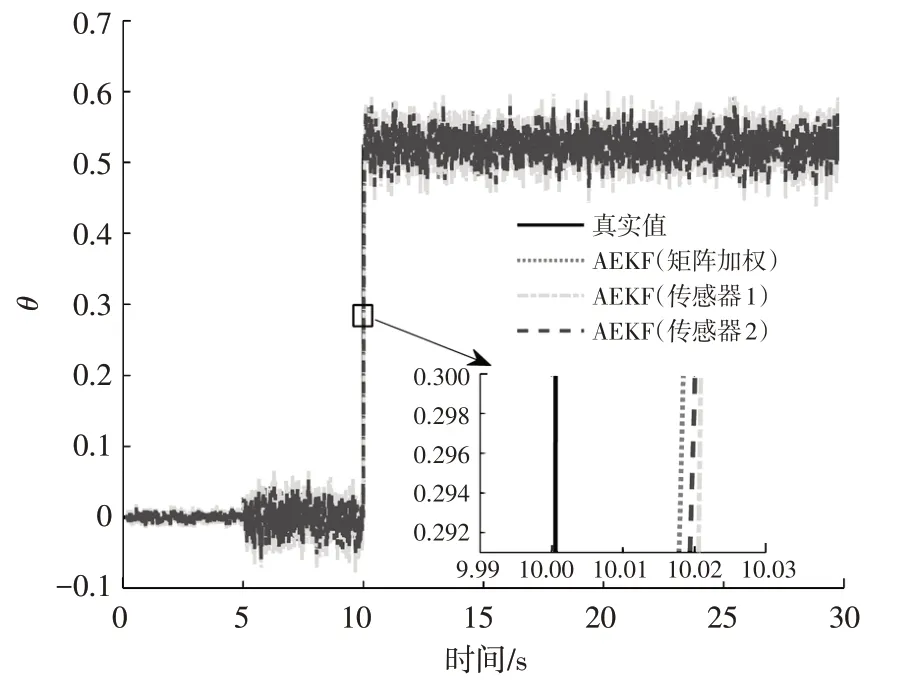
圖6 故障系數估計結果

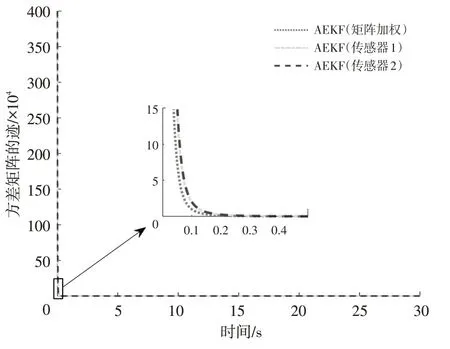
圖7 方差矩陣的跡

由圖3 可知，高精度傳感器（傳感器2）能夠得到更好的估計結果。雖然3 種情形均能保證汽車行駛位置的有效跟蹤，但本文所提出方法的融合估計結果顯然優于單個傳感器的估計結果，精度更高。

由圖4、圖5 可知，本文所提出的方法能夠有效、較好地實現汽車行駛航向角的高精度估計。結合圖3～圖5 可知，本文方法能夠實現自動駕駛汽車位置、航向角和速度的高效估計。

由圖6可知，本文方法還具備執行機構故障的估計能力，且較單個傳感器估計情形具有一定優勢。綜合圖3～圖6可知，本文方法不僅能夠保證自動駕駛汽車在正常狀態下的狀態感知，還可實現故障情形下執行機構故障系數的有效估計，保證了自動駕駛汽車行車全過程的安全、可靠。

由圖7可知，所提出方法的方差矩陣的跡隨著時間推移收斂更快，意味著參數收斂更快。這也是該方法估計結果快速高效的內在原因。

為進一步量化對比所提出方法的優勢，以故障估計誤差的統計學均方誤差（Mean Squared Error，MSE）和誤差標準差（STandard Deviation，STD）為量化指標，將本文方法與對比方法（單個傳感器）統計學信息進行對比，如表2所示。

表2 仿真結果統計學分析

對比表2 中的均方誤差結果可知，矩陣加權AEKF方法的誤差均值最小，則狀態估計效果最佳。進一步對比誤差標準差結果可知，矩陣加權AEKF的跟蹤誤差標準差最小，說明所提出的估計方法與汽車實際狀態的偏差較小，能夠保證誤差估計的快速、平順，從而保證自動駕駛汽車控制系統的穩定運行和行車安全。

5 結束語

針對自動駕駛汽車狀態和故障估計問題，本文在自適應擴展卡爾曼濾波理論基礎上提出了一種矩陣加權多傳感器信息融合估計方法。仿真驗證結果表明，較之單個傳感器的狀態和故障估計方法，所提出的方法能夠較好地實現汽車行駛位置、航向角、速度以及執行機構故障的高效估計，為汽車自動避障、自動泊車等提供一定技術參考。

本文方法雖能實現汽車狀態和故障的有效估計，但由于EKF方法需已知外部擾動和傳感器量測的噪聲統計特性，實際應用中較難準確獲取上述信息，下一步工作將致力于噪聲特性的在線建模，同時嘗試將工程應用中的不同真實傳感器數據源引入本文算法進行實測數據驗證，以期得到工程實用性更強的自動駕駛汽車狀態融合估計方法。