雙樹復小波與寬度學習在軸承故障診斷的應用

張文興，徐佳杰，劉文婧，王建國

（內蒙古科技大學機械工程學院，內蒙古 包頭 014010）

1 引言

隨著科學技術的發展與進步，現代機械設備結構日益復雜，自動化程度也越來越高，同時設備各部分之間的關聯愈加密切。旋轉機械通常需要在惡劣的環境中長時間連續運轉，必然會產生故障，這會導致大量的經濟損失，甚至產生災害［1］。滾動軸承作為一種標準化零件在各種不同類型的機械設備中有廣泛的應用，然而據統計30%的旋轉機械故障和44%的大型電機故障是由軸承故障導致，因此針對軸承的故障診斷有重大的實際意義［2-3］。

小波變換對軸承故障特征進行提取時，基函數的選擇標準難以有效確定，需要操作者依賴經驗進行反復嘗試，工作量大［4］；EMD、EEMD方法能將非平穩數據進行平穩化處理，但計算量大難以對大數據進行特征提取；VMD分解分解層數過大時分量會出現斷斷續續的現象，如何確定分解層數需要人工嘗試。雙樹復小波變換（Dual-Tree Complex Wavelet Transform，簡稱DT-CWT）能夠有效的將信號分解成若干個不同頻帶上的分量且不需要復雜的參數設置，用實部與虛部樹這兩個平行的濾波系統綜合信息，可以更加有效地將不同頻段的信號分解，同時克服了小波變換存在的頻帶混疊、平移可變和信號失真等缺陷，使雙樹復小波在非平穩信號特征提取中具有獨特優勢［4］。

要對經過特征提取操作處理后的信號故障特征的類型進行精確識別，需要使用一種高效、準確的智能分類算法來達到目的。淺層神經網絡存在著只能處理線性分類問題、分類結果精度不夠的先天缺點，無法對高維、多特征數據進行處理。基于深度網絡所構建的模型因其復雜的結構不僅在訓練過程中常常面臨訓練時間過長的問題，且網絡層數與各種超參數設置沒有嚴格的理論依據，嚴重依賴操作者的經驗，可解釋性較差。

寬度學習系統（Broad Learning System，簡稱BLS）作為一種網絡橫向擴展的高效增量學習系統，可有效解決深度學習權值更新慢，無監督、半監督網絡分類成功率低的問題［5］。作為深度學習網絡的替代方法，寬度學習系統以隨機向量函數鏈接神經網絡為映射特征，其本質結構為單隱層神經網絡，通過神經增強節點映射特征并將增強節點直接連接到輸出端［6］。寬度學習神經網絡模型結構更加簡單，性能更加完善，不僅保留了機器學習中深度學習精度高、泛化性能好的優勢，而且彌補了深度學習反向傳播耗時長、收斂慢的缺陷［7］。

2 基本理論介紹

2.1 雙數復小波變換

與常規小波變換不同，雙樹復小波變換由兩個平行且獨立的低通和高通濾波器構成作為實部樹和虛部樹，對在操作過程中數據之間沒有交互和干擾，保留了復小波變換的諸多優良特性［8］。信號在分解時實數部和虛數部之間存在一個采樣值間隔的延時，因此雙數復小波變換在其分解過程中取得的數據行形成互補關系，減少了信息的丟失，在一定程度上抑制了頻率混疊。同時因雙樹復小波具有完全重構性，能對機械振動信號進行完美分解重構，作為一種故障特征提取手段為機械故障類型識別提供了良好的特征［9］。

復小波函數可以表示為：

式中：?h(t)、?g(t)—兩個實數小波；i= -1。

由于雙樹復小波使用的是兩個離散的小波變換，其分解重構過程嚴格遵循小波分析理論，因此經內積運算得到實部變換的小波系數和尺度系數為：

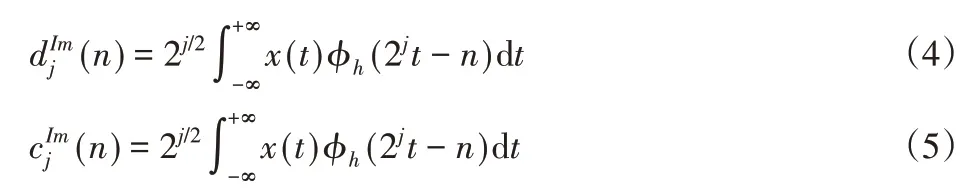
由以上重構算法對雙樹復小波的系數di(t)和cj(t)進行重構為：

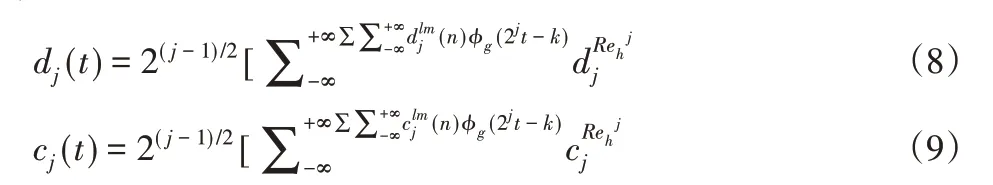
雙樹復小波變換在進行3層分解與重構的具體過程，如圖1所示。h0和h1分別為實部小波分解時所用的低通和高通濾波器；g0和g1分別為虛部小波分解所對應的低通與高通濾波器。同理，和分別為實部小波重構濾波器組和分別為虛部小波重構濾波器組。這里使用的是Q-shift雙樹濾波器以完成小波變換過程［4］。

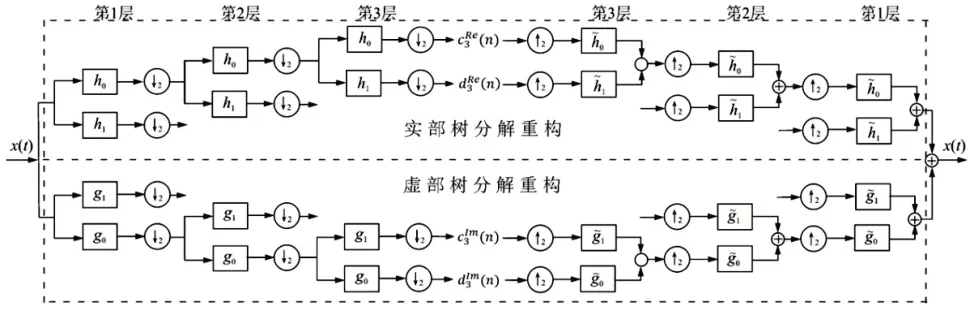
圖1 3層雙樹復小波變換示意圖Fig.1 3 Layer Double Tree Complex Wavelet Transform

經其重構后的信號表示為：

2.2 寬度學習

不同于深度學習基于全局的權值迭代更新的模式，寬度學習系統以原始輸入作為“映射特征”放置在特征節點中，并且結構在“增強節點”中廣義的擴展結構，通過增量學習的模式進行廣泛擴張的快速重建，無需對整個模型進行重新訓練［10］。

特征映射節點Z和增強節點H是寬度學習系統的兩個重要組成部分。對于輸入的訓練數據集X，配有N個訓練樣本，每個訓練樣本有M個維度，Y是RN×X大小的輸出矩陣。對于n個特征映射，每個映射生成k個節點。n個特征映射表示為：

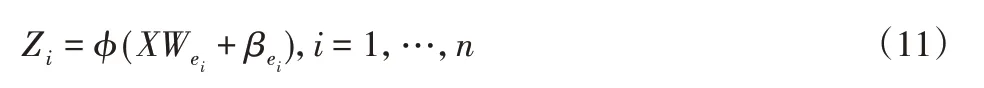
式中：W、β—隨機產生。

將所有的特征節點表示為Zn≡[Z1，…，Zn]，第m組增強節點為：

將原輸入數據的映射節點與由映射節點得到的增強節點一起作為輸入訓練得到輸出：

式中：Wm—寬結構連接權重；Wm=[Zn|Hm]+Y，可以通過[Zn|Hm]+的嶺回歸計算而得。

如果學習精度達不到期望值，可以加入增強節點以達到更好的效果，如圖2所示。Am的更新（擴展）Am+1可表示為：

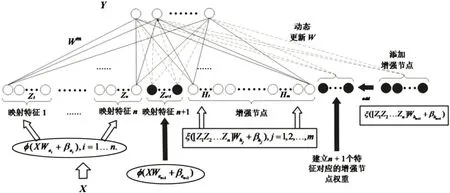
圖2 寬度學習增強節點示意圖Fig.2 Broad Learning System Enhancement Node

其中，Whm+1∈Rnk×p，βhm+1∈Rp。從映射特征到p個附加增強節點的連接權重和偏差是隨機產生的。

3 實驗分析

3.1 振動信號特征提取

在此利用西儲大學風機軸承故障數據說明雙樹復小波變換特征提取效果。以電機轉速為1750r/min，負荷為1.47kW，采樣頻率為12kHz，內圈0.1778mm（0.007英寸）損傷狀態為樣本，信號的時域波形與頻譜，如圖3所示。

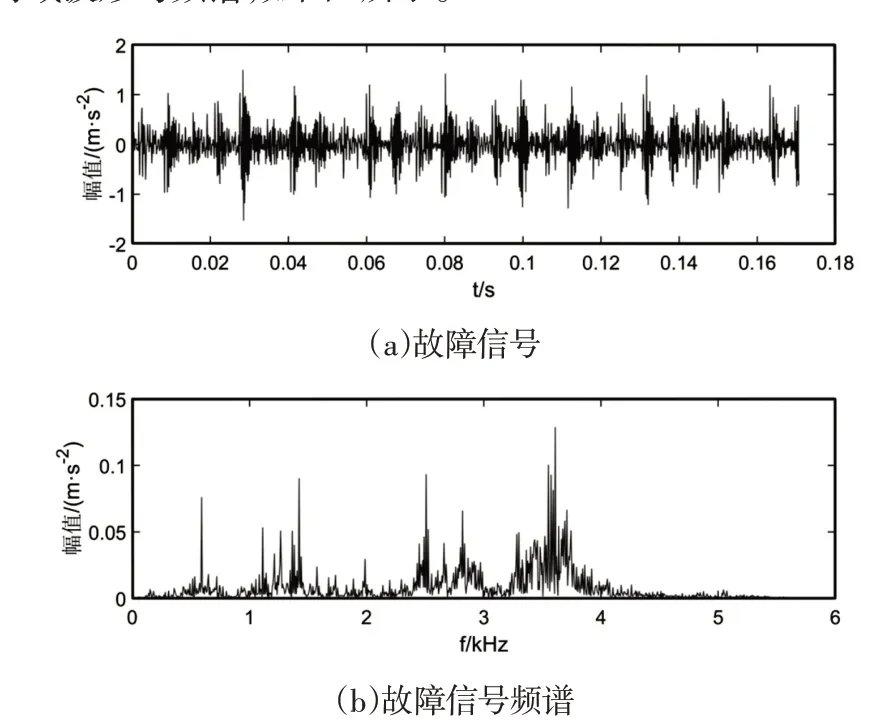
圖3 軸承內圈故障信號及其頻譜Fig.3 Bearing Inner Ring Fault Signal and Frequency

由圖3可以看到特征頻率范圍主要集中在（1～4）kHz。采用雙樹復小波對故障信號進行5層分解后再對單只信號進行重構，重構后所得到的信號分別為高頻分量d1、d2、d3、d4、d5和低頻分量a0，各子帶的信號和頻譜，如圖4所示。

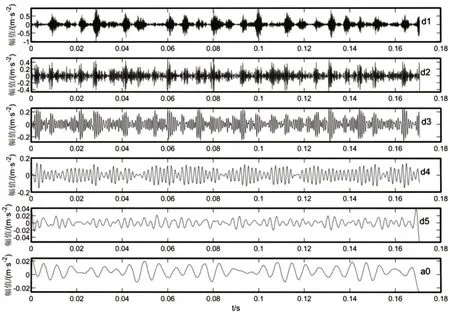
圖4 雙樹復小波分解結果Fig.4 Double Tree Complex Wavelet Decomposition Results

由圖4、圖5可以看出其低頻分量明確，高頻分量僅在d1和d2中存在少量混疊，信號被很好地分解到不同頻帶。d4，d5，a0子帶內信號失真嚴重，無法表征原始故障信號中的沖擊成分；d1子帶內僅有高頻成分，故去除。因此故障的共振帶由具有明顯沖擊成分的d2和d3兩條子帶組成，即得到的最終的故障特征，如圖6所示。

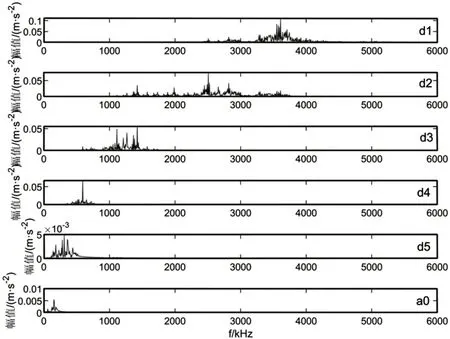
圖5 各子帶的頻譜Fig.5 The Spectrum of Each Subbands

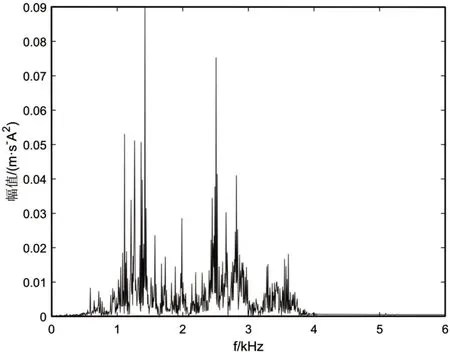
圖6 最終提取的故障特征Fig.6 Extracted Fault Characteristics

將西儲大學在風機轉速1730r/min，負載為2.205kW，采樣頻率為12kHz下正常信號、滾動體故障、內圈故障、外圈故障分別做雙樹復小波變換的特征提取操作，將所得的故障特征進行對比，如圖7所示。可以看出由雙樹復小波變換提取各不同故障類型的故障特征之間有足夠的區分度以完成分類任務。

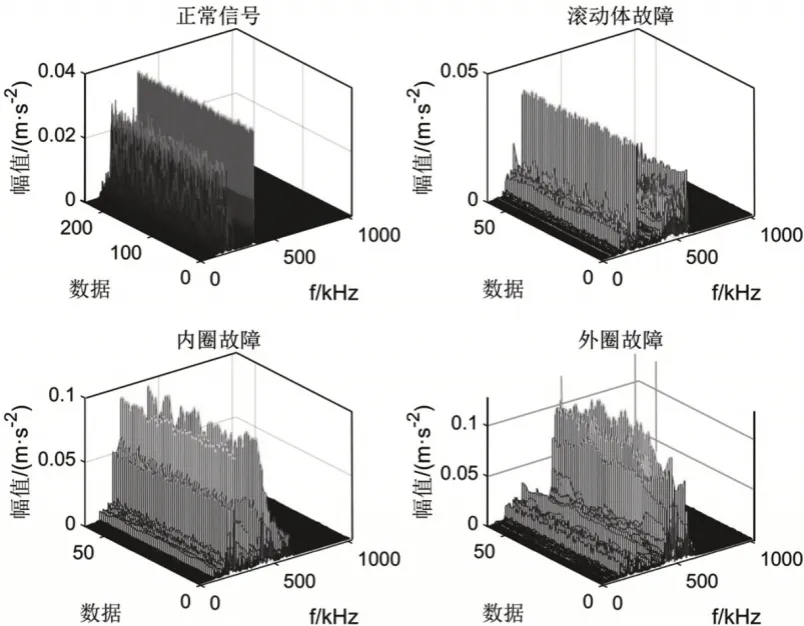
圖7 不同故障特征對比Fig.7 Comparison of Different Fault Features

3.2 數據集制作

利用實驗室軸承故障實驗數據，電機轉速為1200r/min，采樣頻率為12kHz，這里要識別滾動軸承的正常軸承、滾動體故障、內圈故障、外圈故障四種運行狀態。對各種不同故障類型的每條軸承信號分別進行雙數復小波變換的特征提取操作，將所得數據進行歸一化處理變為無量綱數據，整理出的數據集并制作相應的標簽，如表1所示。

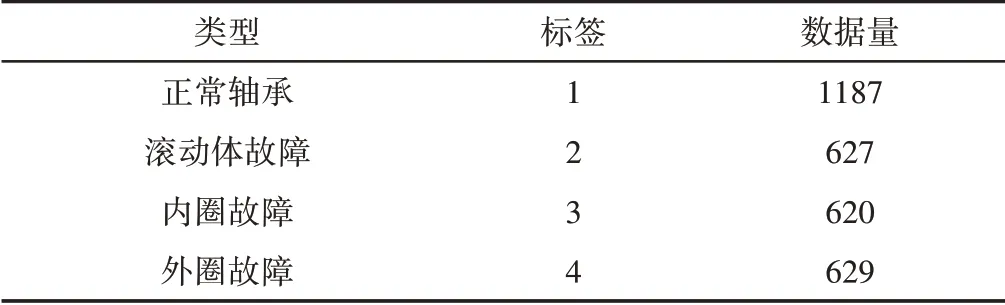
表1 故障類型和標簽Tab.1 Fault Type and Label

3.3 寬度學習診斷

為了體現基于雙樹復小波與寬度學習故障診斷模型的優越性，引入了另外兩種診斷模型進行對比。方案1使用雙樹復小波提取的故障特征，用寬度學習系統診斷；方案2使用雙樹復小波提取的故障特征，用雙隱層BP神經網絡進行診斷；方案3使用頻譜作為故障特征，用雙隱層BP神經網絡進行診斷。不同方案診斷識別率與訓練時間的對比，如表2所示。

表2 訓練效果對比Tab.2 Comparison of Training Effect

4 結論

（1）寬度學習系統能夠在保證識別率的前提下快速地進行增量學習，解決了后期BP 神經網絡反向傳播消耗時長、收斂慢等問題。

（2）基于雙樹復小波變換能夠有效分解離不同成分的信號，在一定程度上針對頻譜中高低頻的冗余特征進行優化，在軸承故障監測與故障識別中比能夠更加有效的將故障特征表示出來。

（3）基于雙樹復小波與寬度學習的滾動軸承故障診斷系統能保證滾動軸承特征提取的診斷準確性和故障診斷的可靠性，在實際工程應用中具有較大潛力。