邏輯類分法在高中數學解題中的應用
?西華師范大學數學與信息學院 張 惠 馮長煥
1 引言
在高中數學解題教學中,題目類型多種多樣,涉及的知識點眾多,解題難度較大.在教與學的過程中,學生常常被難題難住,有時甚至找不到解決問題的突破口.從解題的角度來看,成功解決一道數學問題不僅需要扎實的學科知識,更重要的是要有靈活的方法策略.邏輯類分法是指將原問題劃分為有限多個子問題,然后逐一去解決每一個子問題,最后把各個子問題的結論歸納起來,從而得到整個問題的結論[1].一般地,要進行分類討論的數學問題的邏輯性、探索性較強,運用邏輯類分法解題,能讓問題中不確定的因素轉化為子問題中確定的因素,從而增加問題的條件,使問題變得簡單易于求解.
2 邏輯類分法的內涵
2.1 邏輯類分法的目的與對象
在遇到復雜問題難以解決的時候,可以嘗試將原來復雜的大問題轉化為某些較容易的小問題,化繁為簡、化大為小來幫助求解.在解題中,很多同學認為分類討論的題目很難,從而產生畏懼心理.教師在數學解題教學中,要指導學生明確分類討論的對象,分析問題、明確題目所考查的知識點,然后運用所學知識進行解題.
2.2 邏輯類分法的分類標準
在確定分類討論的對象后,教師要引導學生明確分類討論的標準,從而進行正確合理的分類.引分類討論的原因有很多,于同一個數學問題的研究對象有不同的分類標準:(1)數學中的概念、定理、定義或者函數的性質引起的分類,例如含有絕對值問題的求解、分段函數、函數單調性的探究等[2];(2)數學中的公式、運算法則、圖形的形狀或位置變化引起的分類,例如直線與直線、圓與圓的位置關系;(3)題目中含有參數以及問題的實際情況,例如含有參數的函數問題、方程解的個數問題以及排列、組合中的計數問題.在解題時要根據題目具體要求、題目實際情況的不同而對問題進行具體分析.
2.3 邏輯類分法的特征
運用邏輯類分法解題時所要遵循的規則有:(1)整體簡約性,分類的過程要完整而縝密,周詳而簡約;(2)標準統一性,標準是確定的,每一次分類都要用同一個標準,不允許改變;(3)完備性,子問題不重復不遺漏;(4)逐級遞次性,連續分類要嚴格按照層次逐級進行,不可以越級.在運用邏輯類分法解題時,教師要引導學生把握好各個原則,做到心中有數.
3 邏輯類分法在高中數學教材中的體現
邏輯類分法作為一種常用且普遍的解題方法貫穿于教材中每一個知識點講解之中,人教版高中數學教材無論是必修還是選修內容都對這一思想方法與解題策略的教學尤為重視.通過仔細研究發現,涉及數學運算、圖形位置關系的知識本身就是一種分類討論.例如對于集合之間的運算,要涉及是否為空集的討論;指數與指數冪的運算,對數與對數運算;平面向量的線性運算;不等式的運算;點、直線、平面之間的位置關系;直線與圓的位置關系.涉及概率、函數的性質問題時常常會采用分類討論進行求解,例如拋硬幣、擲骰子;具有典型代表的分段函數、數列、解三角形、三角函數、排列組合、參數方程中都有涉及.
例1(人教版高中數學教材必修一)某市空調公交車的票價按照以下方案制定:(1)5 km以內(含5 km),票價2元;(2)5 km以上,每增加5 km,票價增加1元(不足5 km的按照5 km計算).已知相鄰的公交站距離約為1 km,如果沿途(包括起點站與終點站)有21個公交站,根據題目要求寫出票價與路程之間的函數關系式.
說明:此題主要是分段函數的知識點,屬于典型的分類討論問題,主要由公交車的分段票價引起分類討論.求解這類問題時往往根據題目要求,分類討論,做到不重不漏.
例2(人教版高中數學教材必修二)已知直線l:3x+y-6=0和圓心為C的圓x2+y2-2y-4=0的方程,判斷直線l與⊙C的位置關系;如果相交,則求出兩者交點的坐標.
說明:此題是判斷直線l與⊙C的位置關系,通過圖形的形狀或位置關系引起的分類,這類問題必定會涉及到分類討論.
例3(人教版高中數學教材必修五)在△ABC中,已知a=20 cm,b=28 cm,A=40°,解這個三角形(角度精確到1°,邊長精確到1 cm).
說明:此題考查的知識點是解三角形,主要考查學生對于正弦定理相關知識的掌握和應用.在解答這類問題時往往要對三角形的解的個數進行分類討論.
高中數學教材是學生學習的主要材料,教師不能只限于對數學教材的講解,要結合課程標準要求,創新教學方式,傳授學生知識并教會學生解題.邏輯類分法是一種重要的解題策略,教會學生靈活運用這一策略,培養學生良好的學習習慣與嚴謹的科學態度,幫助學生更加輕松地解題.研究發現在高中數學教材中涉及分類討論的知識繁多,運用邏輯類分法解題的例題和習題也各種各樣,以上例題只是簡單列舉.
4 邏輯類分法在高考題中的應用
數學高考試題注重突出數學學科特色,聚焦核心素養,重視數學思維,倡導理論聯系實際、學以致用,重視讓學生親身體驗數學問題的探索過程,靈活運用數學知識分析數學問題的能力,全面體現了數學學習的基礎性、綜合性、應用性和創新性的考查要求[3].
例4(2021年全國統一高考數學新高考Ⅱ卷第22題)已知函數f(x)=(x-1)ex-ax2+b,討論函數f(x)的單調性.
試題特點:此題主要考查函數單調性的問題.導數法是求解函數單調性的常用方法,其首先對函數f(x)=(x-1)ex-ax2+b進行求導得到f′(x)=xex-2ax=x(ex-2a).由導函數f′(x)=xex-2ax=x(ex-2a)=0解出x時引起分類討論.
解題思路:已知函數的定義域為R,那么f′(x)=xex-2ax=x(ex-2a).
①當a≤0時,令f′(x)>0,所以x<0時,f′(x)<0,f(x)單調遞減;當x>0時,f′(x)>0,f(x)單調遞增.
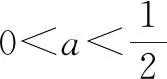
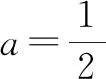
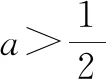
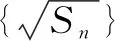
試題特點:數列是高中數學學習的重點以及難點,等差數列與等比數列是其重點學習以及考查內容之一,此題主要考查等差數列及其通項公式的基本應用[4],要求學生靈活運用其定義以及通項公式的知識來解決問題.需要注意的是在求出當n≥2時的通項公式后,不要忘記檢驗n=1是否滿足.
例6(2021年全國統一高考數學全國乙卷理科第23題)已知函數f(x)=|x-a|+|x+3|.
(1)當a=1時,求不等式f(x)≥6的解集;
(2)若f(x)>-a,求a的取值范圍.
試題特點:對于當a=1時,絕對值不等式|x-1|+|x+3|≥6的解法的一般思路是先去掉絕對值:分x≥1,x≤-3,-3 解題思路:(1)a=1時,f(x)=|x-1|+|x+3|,即求|x-1|+|x+3|≥6的解集.當x≥1時,2x+2≥6,得x≥2;當-3 (2)由題意可得f(x)min>-a. 由絕對值的幾何意義可知,f(x)min即為數軸上x到a和-3的距離之和的最小值.當x在a與-3之間時,距離之和最小,此時f(x)min=|a+3|. 所以,|a+3|>-a. 當a<-3時,-a-3>-a,無解. 解題是數學學習的常態活動,在高考題中涉及分類討論的題目往往較難,在日常教學中教師要結合教材內容注重培養學生分類解決問題的意識,掌握這一解題方法,做到靈活應用,正確合理判斷其分類標準以及分類,將問題簡單化. 數學不僅是中學學習的重點內容,也是高考必考科目之一,在學習與考試中都占有極其重要的地位.在素質教育發展的背景下,教師在教學中要幫助學生學習數學知識,掌握解題方法,樹立正確的學習理念,養成良好的學習習慣,全面提升自身綜合能力與數學素養,做到輕松應對高考,實現自己的目標[5].無論是教材中的數學題,還是高考題,用什么方法去解題往往是學生解題的難點與關鍵點.在解題教學中教師要教會學生“怎樣想”,引導學生對知識本質的理解,讓學生自己去探究與領悟,親身經歷知識的發生與發展過程. 學會解題需要長期的模仿與練習,解決一道數學問題不僅需要具備扎實的專業知識,還需要掌握靈活的解題策略.邏輯類分法在數學解題中有著舉足輕重的作用和地位,教師在教學中要有意識地滲透這種解題策略,幫助學生更好地掌握和運用.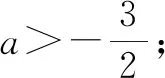
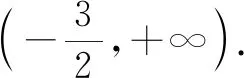
5 結論

