汽車尾燈支架裝配變形的數值模擬與驗證

王鵬，羅帥，姜偉民

汽車尾燈支架裝配變形的數值模擬與驗證

王鵬，羅帥，姜偉民

（上汽通用汽車有限公司 整車制造工程部，上海 201206）

深入研究汽車尾燈裝配變形，建立可以精確預測尾燈裝配變形的有限元方案。通過數字圖像相關法研究了尾燈緊固過程中鈑金支架的變形情況，獲得了支架上關鍵位置的變形規律。引入有限元仿真分析方法，建立了全工況有限元仿真分析模型，對尾燈裝配的整個過程進行數值仿真。獲得了裝配后鈑金變形量的預測值，通過對3類尾燈的裝配過程進行仿真分析，對比實際測量的鈑金支架變形數據，驗證了該模型能夠較為精確地預測尾燈裝配中的變形誤差。提出了尾燈裝配定位基準與螺栓緊固點分離的解決方案，從設計上有效避免了新車型尾燈裝配超差問題的產生。

汽車尾燈；數字圖像相關法；計算機輔助工程分析；裝配變形；誤差控制

隨著汽車工業的智能化與自動化的不斷推進，整車從設計到完成批量生產的時間被大量壓縮，許多設計問題往往需要等到樣車試制階段才能被發現，進而產生了高昂的模具更改費用。為此需引入先進的分析方法，例如在車頂焊接[1]、橡膠管卡箍變形[2]等較復雜工況的研究中使用非線性有限元仿真，提前識別汽車零部件的設計缺陷，以節省大量的時間與開發費用。對于汽車車燈，多數學者開展了針對車燈本身的造型設計、光學設計以及注塑工藝改進的相關研究。馮鈺濤[3]通過CAD/CAE研究了尾燈的設計與制造，優化改進了車燈設計中的凝霧現象。葉盾[4]通過力學分析了汽車車燈卡扣的寬度和高度對其力學性能的影響，獲得了最佳的設計參數。唐杰等[5]通過CAE模擬仿真確定了汽車燈罩的最佳澆口位置及工藝參數。這些研究對零件本身進行了優化與改進，但在整車的生產制造中，許多質量缺陷在零件與零件安裝配合后才能被識別，這類缺陷的辨識是非常困難以及滯后的，如何提前辨識出此類質量缺陷是擺在眾多工程師面前的難題。周煒等[6]針對白車身門、框匹配問題，提出了在計算機虛擬環境下，利用三坐標測量數據，快速、準確檢測零件質量問題。陳強等[7]通過有限元方法研究了轎車尾燈區域螺母裝配過程中裝配力和裝配順序引起的裝配偏差規律，有力指導了實際生產。劉文杰等[8]借助Autoform軟件對汽車縱梁進行沖壓成形模擬和回彈補償模擬，經過多次回彈補償，將零件的最大回彈由補償前的13 mm減小至±0.5 mm以內。

在汽車尾燈設計中，除了必要的外觀造型要求之外，其與后舉門之間的尺寸匹配質量是整車制造的重要關注點，圖1a展示了汽車尾燈與后舉門之間需要滿足的尺寸匹配技術要求，其中間隙要求如下：公差為±0.8 mm，一致性為1 mm；平整度要求如下：公差為±0.8 mm。由圖1b可知，尾燈通過螺柱緊固在汽車后舉門的鈑金支架上，在尾燈與支架之間裝配著一圈泡棉，起到密封和防水的作用。圖1c為汽車尾燈結構，其定位結構有螺柱基座、尾燈掛鉤和定位銷，其中螺柱基座和掛鉤用于尾燈安裝時前后方向定位，定位銷用于尾燈安裝時高低和左右方向定位，定位結構決定了尾燈裝配質量是否達標。雖然尾燈的設計有相關的設計規范，但由于安裝時零件與零件之間相互作用力的影響，時常導致尾燈安裝后產品質量超差。針對此類問題，目前的解決方案多為根據工程師以往的項目經驗進行定性分析，以此作為設計依據，零件制造出來后再進行實物驗證，如果出現問題，就從設計、工藝等角度尋找補救方案，這一流程會產生較大的費用。為此，文中通過引入CAE分析方法，對汽車尾燈裝配過程進行全工況有限元仿真，建立了可準確識別尾燈安裝缺陷的CAE分析方法，從而在汽車尾燈設計的早期就可以辨識安裝缺陷，減少后續制造裝配階段的返工。

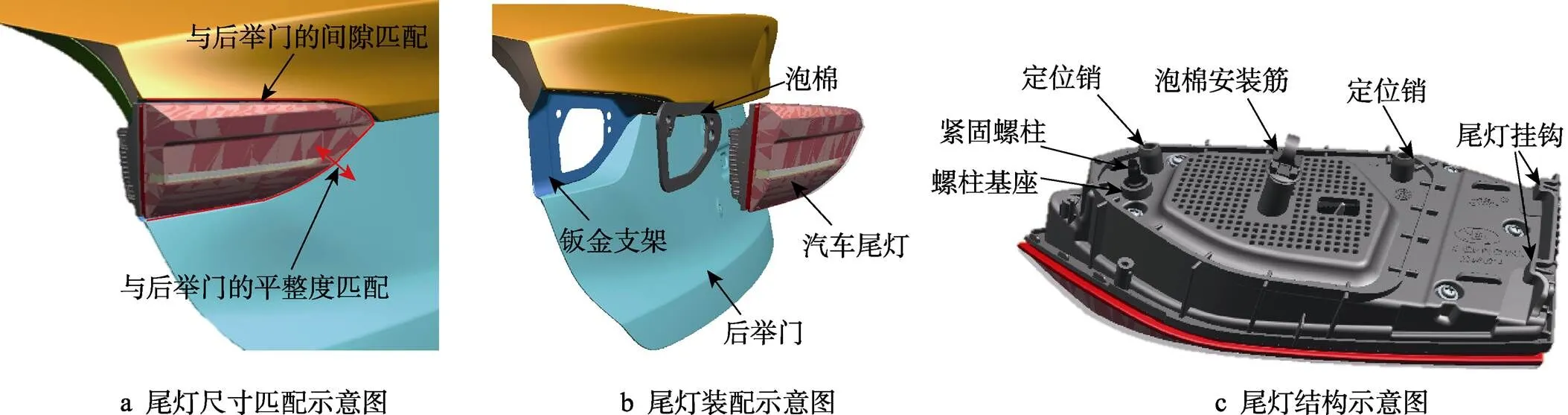
圖1 汽車尾燈示意圖

1 材料性能及鈑金變形量的測定

材料力學性能數據的準確性會直接影響有限元分析結果的精度。對于汽車尾燈裝配的全工況CAE仿真，其裝配誤差要求是不大于0.1 mm，因此正確獲取材料性能參數十分重要。汽車尾燈在安裝過程中涉及的變形材料有泡棉和鈑金支架，尾燈燈體自身在裝配過程中的變形可以忽略不計。

1.1 鈑金及泡棉的力學性能測量

泡棉屬于橡膠類材料，具有復雜的力學性能，一般采用超彈性應變勢能函數描述其力學性能[9]。泡棉在尾燈的裝配過程中主要產生壓縮變形。根據GB/T 2941—2006和ASTM D1095—2014，設計了測定泡棉壓縮力學性能的試驗。在萬能試驗機上進行準靜態試驗，壓縮速度設置為10 mm/min。泡棉試樣尺寸為：直徑（29±0.5）mm，厚度12 mm，當產品厚度不夠時，經實驗對比，可采用疊加的方式。試驗所取的試樣形狀、尺寸、位置及獲得的工程應力–應變曲線如圖2a所示。對于鈑金支架，則進行拉伸性能的測定，試驗所取的試樣形狀、尺寸、位置及獲得的真實應力–應變曲線如圖2b所示。

1.2 鈑金支架變形量測量

為研究鈑金支架在螺柱緊固過程中的變形情況，采用數字圖像相關法（Digital Image Correlation，DIC）[10]對緊固過程進行位移場捕捉。如圖3a所示，DIC設備的高速相機不斷地對尾燈緊固過程進行拍攝，通過對比變形結束與初始的圖片，得出鈑金支架的變形情況，變形量為正值表示支架的變形方向是車輛前部。如圖3b所示，受泡棉壓縮反力的影響，鈑金支架中部拱起，朝車前變形0.6 mm，螺母孔處的鈑金受螺栓預緊力的影響，朝車后變形0.9 mm。螺母孔處的鈑金與尾燈前后方向的定位結構（螺柱基座）配合，鈑金變形直接使尾燈空間位置發生變化，進而影響尾燈與后舉門的尺寸配合。如圖3c和d所示，提取螺母孔附近關鍵點的位移，得到關鍵點在緊固過程中的位移變化情況，可以發現點1與點3之間的位移差即為螺母孔處的鈑金變形量，這是因為點3位置的鈑金支架剛性較強，在螺母緊固過程中僅發生剛性位移，而螺母孔處的鈑金受預緊力的影響同時發生變形位移和剛性位移。

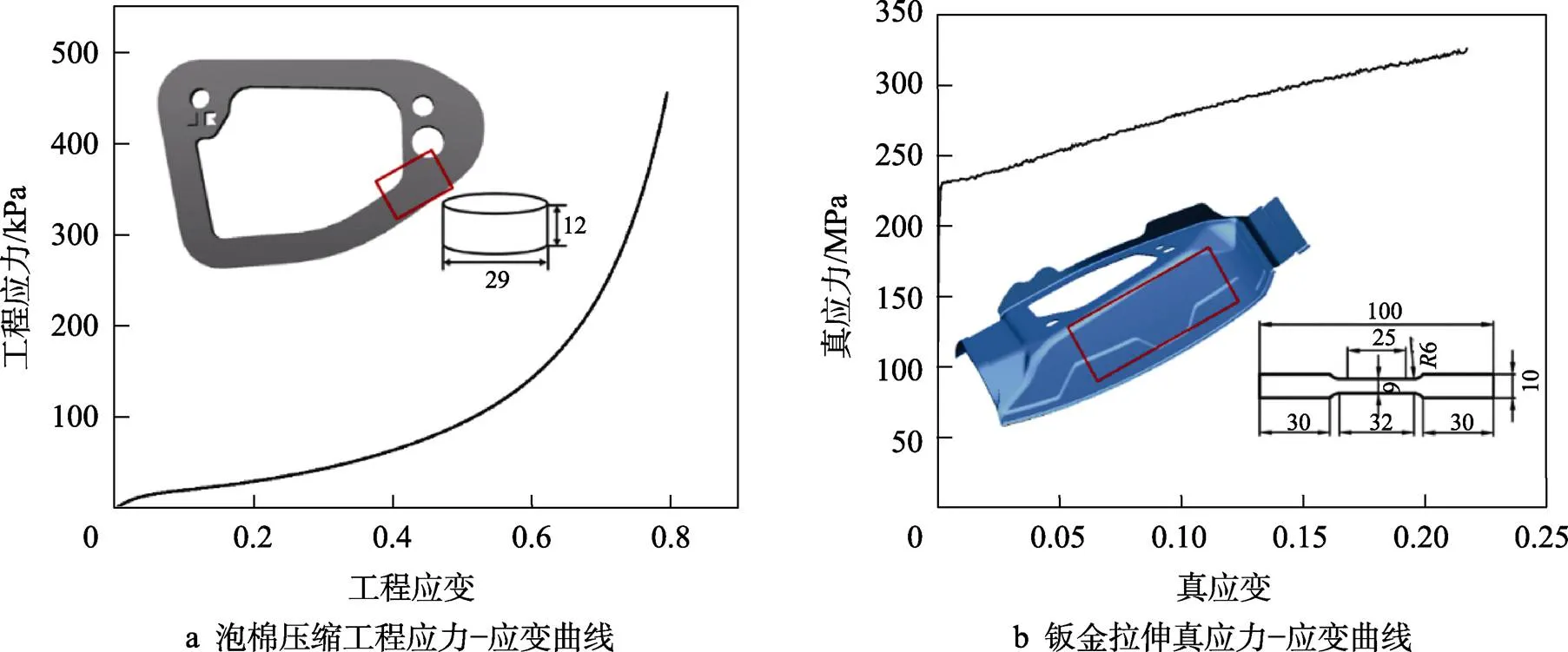
圖2 材料力學性能曲線

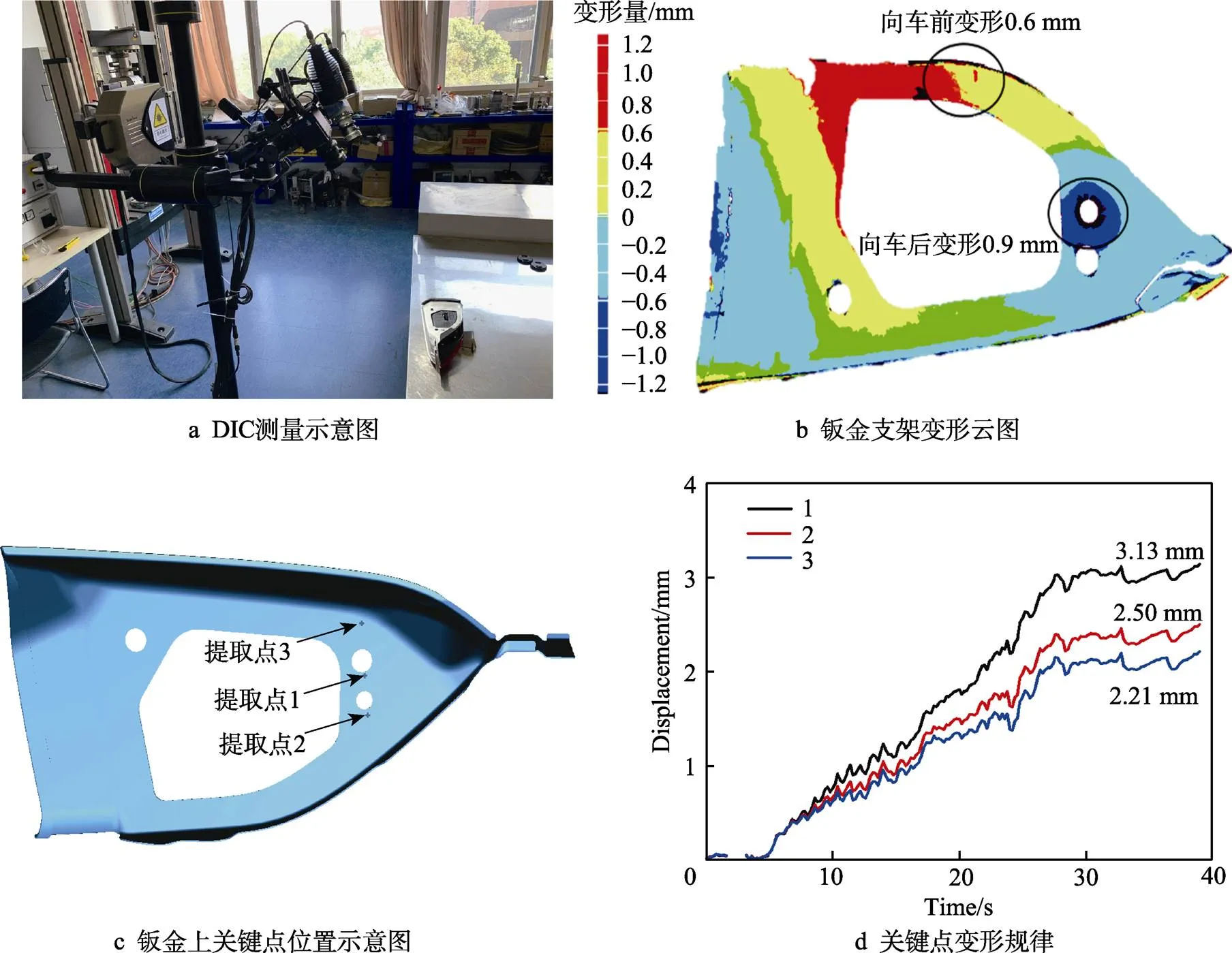
圖3 DIC測量結果

2 CAE析模型的建立

如圖4a所示，尾燈的安裝過程是尾燈掛鉤首先卡接于鈑金支架，然后以尾燈掛鉤為轉軸旋轉尾燈，使定位銷和螺柱穿過支架的安裝孔，最后用緊固螺母固定尾燈。為提高分析精度和簡化CAE分析時載荷的施加，文中提出如下的尾燈裝配全工況CAE仿真分析方法。

實際安裝過程是鈑金固定，移動尾燈，CAE分析中為簡化螺母緊固的過程，采用固定尾燈，直接對鈑金施加螺栓預緊力的分析方法。具體過程如圖4b—e所示，將尾燈CAE分析模型分為數模、初始、預壓和緊固等4個階段。如圖4b所示，在數模階段，對零件數模進行網格劃分，鈑金采用殼單元網格，大小設置為1～3 mm，在主要變形區采用1 mm網格；螺栓、泡棉、燈罩采用實體C3D8R單元，全局種子設置為0.5 mm，由于整車數模狀態下的泡棉與鈑金處于干涉狀態，無法直接進行計算分析。如圖4c所示，在初始階段，為模擬尾燈裝配過程，調整鈑金支架與泡棉的相對位置，達到CAE計算分析的初始階段。調整的方法如下：以尾燈掛鉤為轉軸，向遠離燈罩的方向旋轉鈑金支架5°左右，消除鈑金與泡棉的干涉。模型設置方面，將燈罩設置為剛體，泡棉底部與燈罩設置Tie連接，螺母與鈑金設置Tie連接，在接觸設置中，摩擦因數設置為0.2。在預壓階段如圖4d所示，由于泡棉的壓縮仿真涉及材料非線性、邊界非線性和幾何非線性[11]，直接施加螺栓預緊力會導致計算收斂困難，故首先在鈑金支架的螺母孔處施加一個較小的力（小于100 N），使鈑金與泡棉建立平穩的接觸關系。在緊固階段如圖4e所示，將螺栓預緊力施加在鈑金支架的螺母孔處，仿真分析鈑金支架在打緊過程中和打緊之后的變形情況。計算步設置見表1。

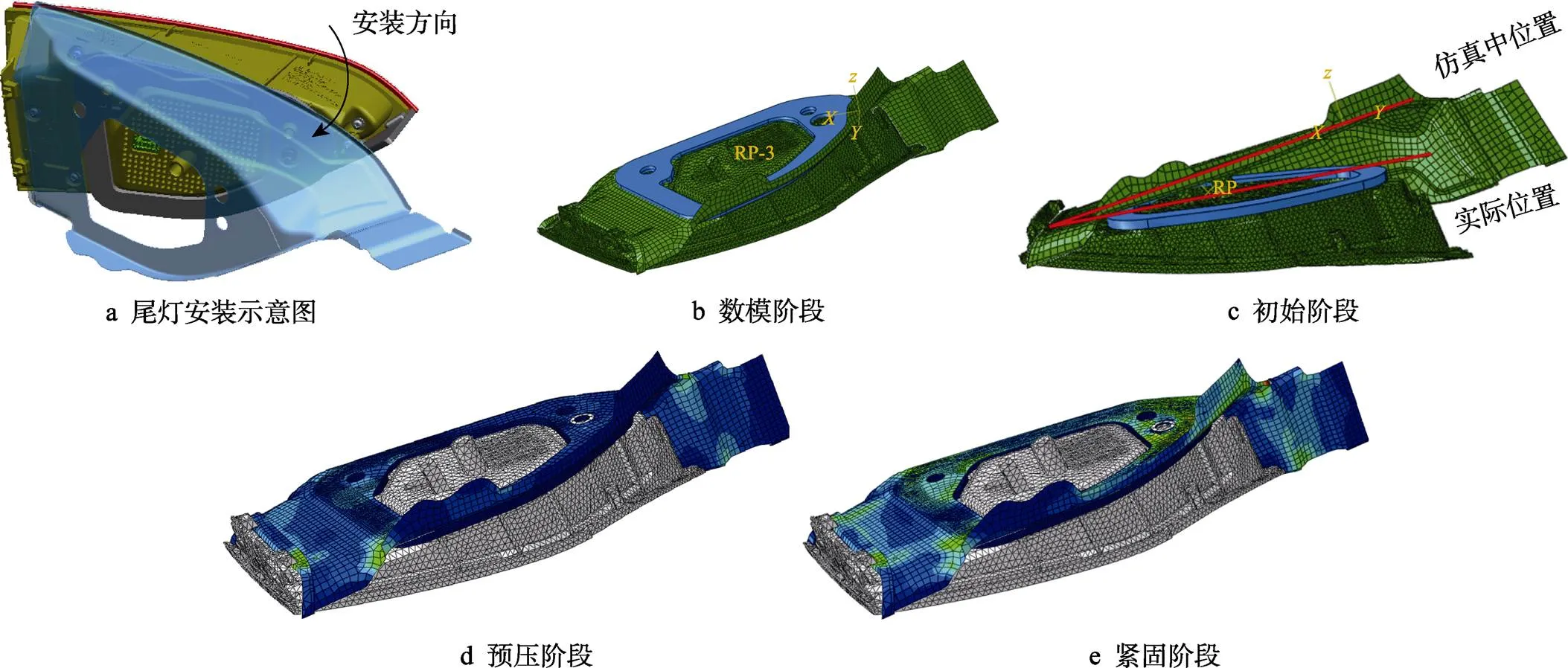
圖4 尾燈全工況CAE分析模型的建立

表1 計算步設置

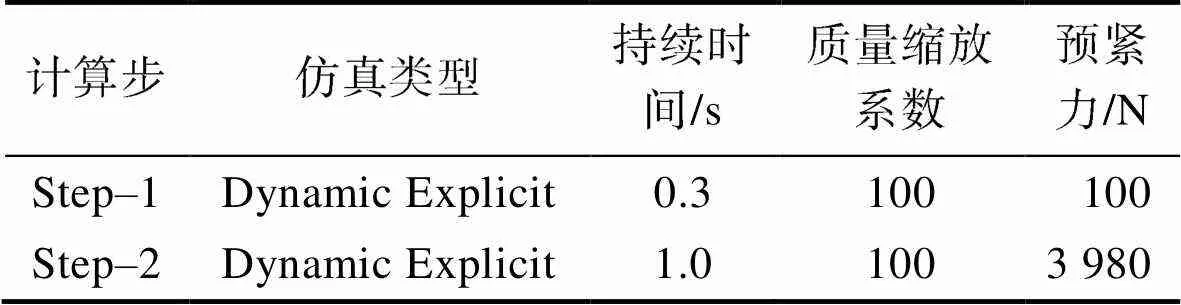
Tab.1 Calculation step set

在ABAQUS中建立全工況仿真模型時，選擇合適的泡棉超彈性本構模型十分重要[12]。李凡珠等[13]對橡膠材料進行了循環加載的本構關系測量實驗并進行數值擬合，發現采用Marlow[14]和Ogden等[15]提出的超彈性本構方程可以更精確描述橡膠材料的本構關系。根據泡棉的實驗數據以及尾燈裝配方式，文中采用Marlow本構模型來描述尾燈泡棉的超彈性特征。Marlow模型如式（1）所示。

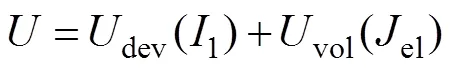
式中：為單位體積的應變能量；dev為偏應變能量；vol為體積應變能量；1為第一偏應變不變量，其定義如式（2）所示。各個方向的偏應變可以用式（3）表示。

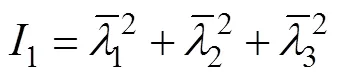
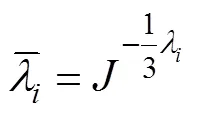
式中：為總容積比率；el為熱膨脹下定義的彈性容積比；λ為各個方向的主應變。偏應變能量可以通過單軸試驗、等效雙軸試驗或者平面試驗獲得。體積應變能量部分可以通過體積應變試驗確定泊松比，或者通過單軸試驗、等效雙軸試驗或者平面應變試驗獲得。

3 實驗驗證及分析

3.1 鈑金變形量的準確識別

鈑金支架在有限元分析過程中會產生剛性位移和變形，建立識別變形量的方法十分關鍵。如圖5所示，螺母緊固后，泡棉的壓縮力會使鈑金偏離理想位置，需要準確識別相應的鈑金變形量。如圖6所示，CAE分析模型以尾燈掛鉤為轉軸，當沒有泡棉時，進行全工況CAE仿真，此時與轉軸平行的平行線上所有節點的位移都是相同的，皆為剛性位移，螺母孔處未發生變形。當有泡棉時，平行線上的節點分為變形節點和未變形節點，未變形節點只發生剛性位移，變形節點同時發生剛性位移和變形，找出變形點和未變形點，兩者的位移之差即可表示螺母孔處鈑金的變形量。在具體操作時，如圖6b所示，以旋轉軸為軸線，以鈑金螺栓孔中心到軸線的距離為半徑繪制圓柱，圓柱與螺母邊緣的交點為變形點，與鈑金大平面邊緣的交點為未變形點。

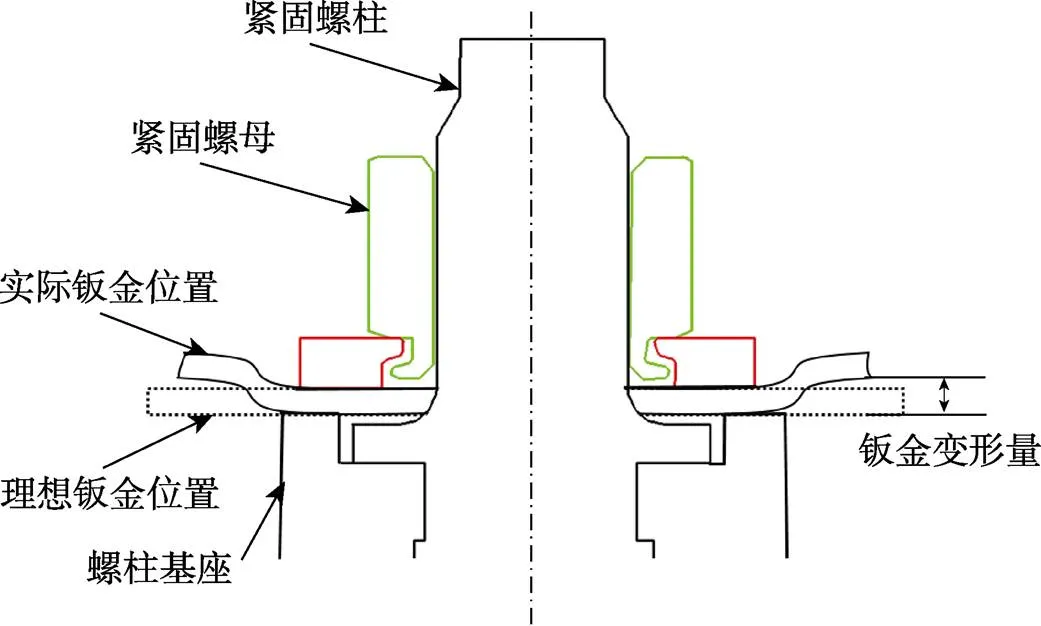
圖5 鈑金變形示意圖

3.2 實際測量與仿真結果的對比

為了驗證CAE模型的準確度，選擇了3款車型的車燈（見圖7）進行CAE仿真和實物試驗，結果如表2所示，對Ⅰ、Ⅱ、Ⅲ這3款車燈進行全工況CAE仿真，提取其中的變形點與未變形點的位移數據，計算得到螺母孔處的變形量，對比實際測得的變形量，Ⅰ和Ⅲ的誤差值不超過0.1 mm，Ⅱ的誤差值稍超出0.1 mm，總體上滿足工程上的精度識別要求，說明上述開發的全工況CAE仿真模型可對尾燈裝配變形實現較為精準的預測，能夠提前判斷尾燈是否存在設計缺陷。

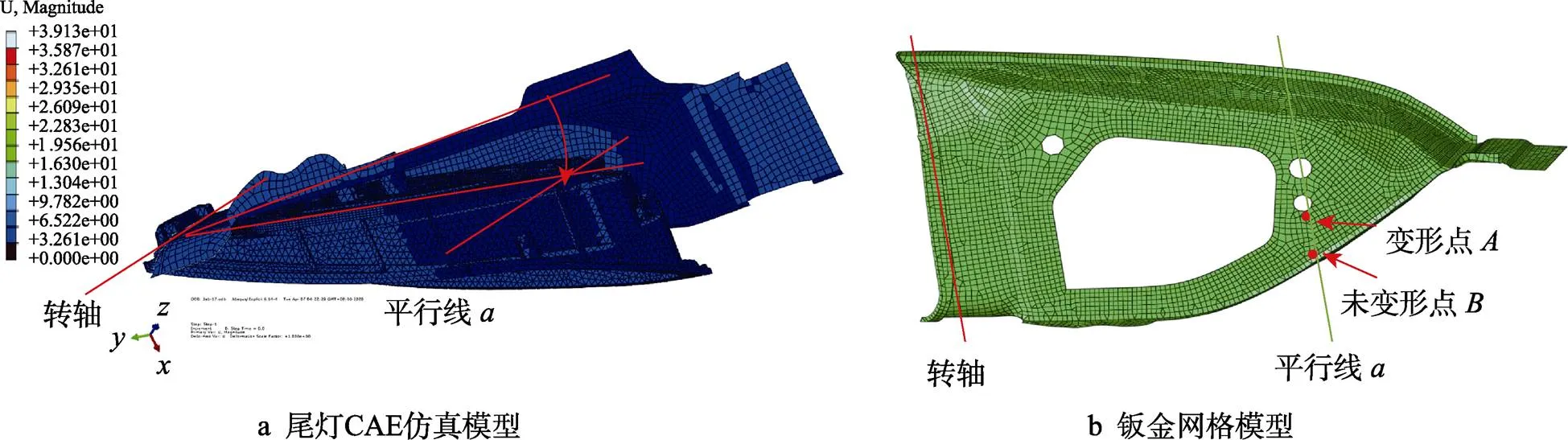
圖6 全工況CAE分析模型

圖7 3款車型的車燈

表2 3款汽車尾燈裝配后鈑金支架變形量對比

Tab.2 Comparison of deformation of sheet metal bracket of three taillights after assembly

3.3 超差原因分析及解決方案

Ⅰ、Ⅲ兩款車燈都應用了大泡棉和以螺柱基座為定位基準的設計策略，在緊固螺母后，泡棉的壓縮反力和螺母的壓力使鈑金支架發生變形，導致尾燈偏離設計位置，引發尾燈與后舉門的尺寸匹配超差。綜合對比上述有限元分析結果和相關實測數據，發現當定位基準與螺栓緊固點處于同一位置時，出現裝配超差問題的概率較大（見圖8a）。如圖8b所示，在滿足造型要求的前提下，可執行基準分離策略，使螺柱僅有緊固作用。在螺柱四周設置一圈包圍結構充當定位基準，這樣螺母孔處的鈑金變形就不會影響整個尾燈的定位。

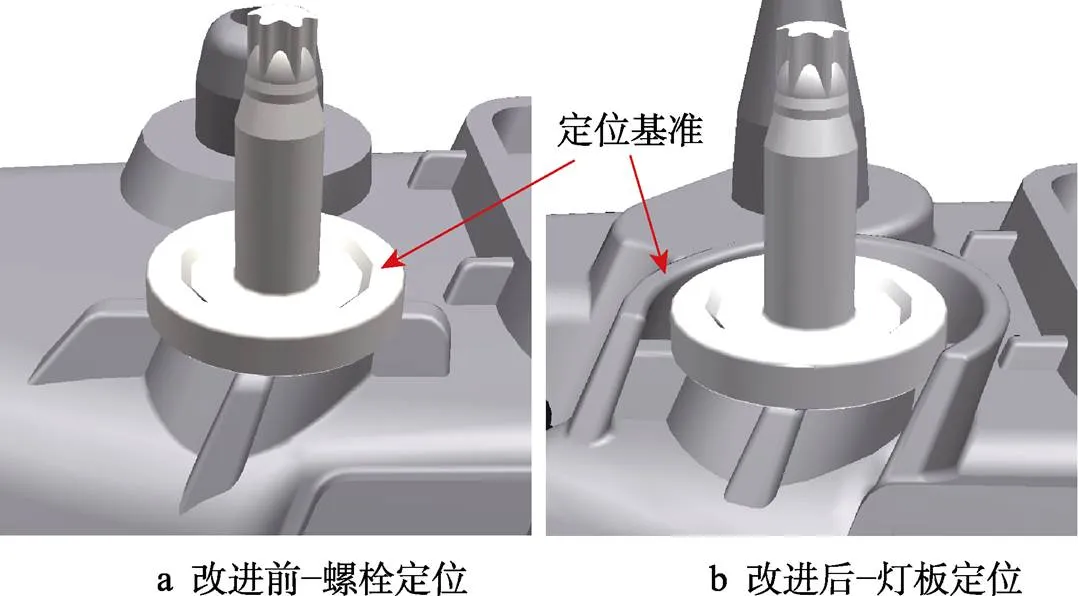
圖8 定位基準與緊固點分離

4 結論

在深入研究尾燈實際安裝變形超差問題的基礎上，建立了一種識別尾燈裝配變形的全工況CAE仿真分析模型。采用該模型進行了3款車燈裝配變形的有限元仿真分析，結果表明，該CAE分析模型能夠在設計的早期較為精確地預測尾燈裝配超差缺陷，預測裝配誤差與實驗測得的實際誤差總體吻合，有效發現了潛在風險，從而降低了項目成本。在此基礎上，進一步提出了尾燈裝配定位基準與螺栓緊固點分離的解決方案，在螺柱四周新設計一圈包圍結構充當定位基準，從設計上有效避免了新車型尾燈裝配超差問題的產生。

[1] 余魁, 朱亮, 陸磊, 等. 白車身頂蓋激光釬焊焊縫裝配尺寸控制方法研究[J]. 精密成形工程, 2019, 11(4): 140-146.

YU Kui, ZHU Liang, LU Lei, et al. Control Method of BIW Roof Laser Beam Braze Welding Joint Assembly Dimensional Accuracy[J]. Journal of Netshape Forming Engineering, 2019, 11(4): 140-146.

[2] 劉曉兵, 槐艷松, 邵杰, 等. 卡箍夾緊變形過程及力學性能分析[J]. 精密成形工程, 2020, 12(6): 175-180.

LIU Xiao-bing, HUAI Yan-song, SHAO Jie, et al. Clamping Deformation Process and Mechanical Properties of Clamp[J]. Journal of Netshape Forming Engineering, 2020, 12(6): 175-180.

[3] 馮鈺濤. 基于CAD/CAE技術的汽車車燈的設計研究與應用[D]. 武漢: 湖北工業大學, 2019: 15-22.

FENG Yu-tao. Research and Application of Automobile Lamp Design Based on CAD/CAE Technology[D]. Wuhan: Hubei University of Technology, 2019: 15-22.

[4] 葉盾. 基于力學分析的汽車車燈卡扣結構優化設計[J]. 汽車零部件, 2018(12): 54-58.

YE Dun. Optimized Design for Snap Structure of Automobile Lamp Based on Mechanical Analysis[J]. Automobile Parts, 2018(12): 54-58.

[5] 唐杰, 黃榮學, 王全亮, 等. CAE技術在汽車燈罩設計中的應用[J]. 模具工業, 2020, 46(3): 12-17.

TANG Jie, HUANG Rong-xue, WANG Quan-liang, et al. Application of CAE Technology in Design of Automobile Lampshade[J]. Die & Mould Industry, 2020, 46(3): 12-17.

[6] 周煒, 張淑敏, 林忠欽, 等. 虛擬環境下的白車身門、框匹配問題研究[J]. 機械設計與制造, 2002(4): 82-84.

ZHOU Wei, ZHANG Shu-min, LIN Zhong-qin, et al. The Fitting Problem Study on the Door and Body-in-White in Detail[J]. Machinery Design & Manufacture, 2002(4): 82-84.

[7] 陳強, 李志敏, 王華. 裝配力引起的轎車尾燈裝配偏差有限元分析[J]. 機械設計與制造, 2011(12): 28-30.

CHEN Qiang, LI Zhi-min, WANG Hua. Research on Deviation of Car Taillight Caused by Assembly Force Using FEA[J]. Machinery Design & Manufacture, 2011(12): 28-30.

[8] 劉文杰, 雷聲. 汽車縱梁成形回彈及補償[J]. 精密成形工程, 2019, 11(3): 127-132.

LIU Wen-jie, LEI Sheng. Forming Springback and Compensation of Auto Girder[J]. Journal of Netshape Forming Engineering, 2019, 11(3): 127-132.

[9] 彭向峰, 李錄賢. 超彈性材料本構關系的最新研究進展[J]. 力學學報, 2020, 52(5): 1221-1232.

PENG Xiang-feng, LI Lu-xian. State of the Art of Constitutive Relations of Hyperelastic Materials[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(5): 1221-1232.

[10] 李耿, 殷咸青, 牛靖, 等. 采用光學測量技術研究鋁合金焊接變形[J]. 精密成形工程, 2020, 12(1): 92-97.

LI Geng, YIN Xian-qing, NIU Jing, et al. Welding Deformation of Aluminum Alloy by Optical Measurement Technology[J]. Journal of Netshape Forming Engineering, 2020, 12(1): 92-97.

[11] 周萬里, 黃攀. 基于ABAQUS和EXCEL的泡棉靜態力學性能分析[J]. 科技風, 2017(9): 22.

ZHOU Wan-li, HUANG Pan. Static Mechanical Properties Analysis of Foam Based on ABAQUS and Excel[J]. Technology Wind, 2017(9): 22

[12] 趙建才, 姚振強. 桑塔納2000車門密封條壓縮變形的數值分析[J]. 上海交通大學學報, 2006, 40(10): 1806-1808.

ZHAO Jian-cai, YAO Zhen-qiang. The Numerical Simulation of Compression Deformation of Santana 2000 Seal[J]. Journal of Shanghai Jiao Tong University, 2006, 40(10): 1806-1808.

[13] 李凡珠, 劉金朋, 盧詠來, 等. 填充橡膠材料循環加載的本構行為及數值擬合[J]. 橡膠工業, 2017, 64(2): 79-83.

LI Fan-zhu, LIU Jin-peng, LU Yong-lai, et al. Modeling on Constitutive Behaviors of Filled Rubber Compounds for Cyclic Loading Path[J]. China Rubber Industry, 2017, 64(2): 79-83.

[14] MARLOW R. A General First-Invariant Hyperelastic Constitutive Model[J]. Constitutive Models for Rubber, 2003, 3(1): 157-160.

[15] OGDEN R W, ROXBURGH D G. A Pseudo-Elastic Model for the Mullins Effect in Filled Rubber[J]. Proceedings: Mathematical, Physical and Engineering Sciences, 1999, 455(1988): 2861-2877.

Numerical Simulation and Experimental Verification of Assembly Deformation of Automobile Tail Lamp Sheet Metal Bracket

WANG Peng, LUO Shuai, JIANG Wei-min

(Vehicle Manufacturing Engineering, SAIC-GM, Shanghai 201206, China)

The tail lamp assembly deformation is deeply studied, and the finite element scheme which can accurately predict the tail lamp assembly deformation is established. Through the digital image correlation method, the deformation of the sheet metal bracket during the fastening process of the tail lamp is studied, and the deformation law of the key position on the bracket is obtained. The finite element simulation analysis method is introduced to establish the full condition finite element simulation analysis model. The numerical simulation of the whole process of tail lamp assembly is carried out, and the predicted value of sheet metal deformation after assembly is obtained. Through the simulation analysis of three types of tail lamp assembly process, compared with the actual measured deformation data of sheet metal bracket, the model can accurately predict the deformation error of tail lamp assembly.On this basis, the solution of separating the tail lamp assembly positioning datum from the bolt fastening point is further proposed, which effectively avoids the problem of out of tolerance in the new model tail lamp assembly.

tail lamp; digital image correlation; CAE analysis; assembly deformation; error control

10.3969/j.issn.1674-6457.2022.05.009

U463

A

1674-6457(2022)05-0055-06

2021–06–21

部門咨詢費項目

王鵬（1981—），男，工程師，主要研究方向為汽車制造。

責任編輯：蔣紅晨