N型PM函數(shù)的非單調(diào)高度

吳 馗, 李 林, 朱 紅, 陳嘉怡

(嘉興學(xué)院 數(shù)據(jù)科學(xué)學(xué)院, 浙江 嘉興 314001)

給定正整數(shù)n和一個(gè)有限區(qū)間I?R,如果

fn(x)=F(x), ?x∈I,

作為動力系統(tǒng)和函數(shù)方程理論的一個(gè)重要課題,迭代根問題已經(jīng)在各個(gè)方面進(jìn)行了深入的研究.除了早期Babbage[1]、Schr?der[2]和B?dewadt[3]的工作外,Kuczma[4-5]于1961年對區(qū)間上的單調(diào)自映射迭代根給出非常漂亮的結(jié)果.值得一提的是,Kuczma等[6-7]又系統(tǒng)闡述了單調(diào)迭代根的構(gòu)造理論.由于單調(diào)迭代根中的逐段定義法無法應(yīng)用于非單調(diào)的情形,非單調(diào)迭代根一直是個(gè)非常復(fù)雜的問題.

1983年,張景中等[8]率先引入逐段單調(diào)函數(shù)(簡稱PM函數(shù)),并通過定義此類函數(shù)的非單調(diào)高度來刻畫迭代根的存在性,提出特征區(qū)間的概念.具體地說,PM函數(shù)非單調(diào)高度為1的等價(jià)條件是該函數(shù)存在特征區(qū)間.在文獻(xiàn)[9-14]中,針對函數(shù)的非單調(diào)高度,學(xué)者分別提出非單調(diào)高度等于1和大于1情形下迭代根的兩個(gè)公開問題.隨后,對于這2個(gè)公開問題,陸續(xù)取得一些進(jìn)展.例如,孫太祥等[11,14]討論了單位區(qū)間上所有N型和反N型函數(shù)的迭代根問題;Zhang等[15-16]得到一類保端點(diǎn)且非單調(diào)高度等于迭代指數(shù)的多峰映射不存在C0迭代根的充分條件.

最近,該結(jié)果又被推廣到非保端點(diǎn)的情形,徹底解決迭代指數(shù)臨界狀態(tài)下的迭代根問題[17].Liu等[13]將迭代根分成“幾乎遞增”的τ1類與“幾乎遞減”的τ2類,并得到映射存在τ1類迭代根的充分必要條件.但要注意的是,上述的結(jié)果主要是處理非單調(diào)高度為有限值的情況.文獻(xiàn)[17]證明高度為無窮的PM函數(shù)在所有PM函數(shù)集合中是稠密的.因此,討論函數(shù)的非單調(diào)高度,特別是非單調(diào)高度為無窮的情況對研究PM函數(shù)的動力學(xué)性質(zhì)至關(guān)重要.

為了證明的闡述更為清楚,本文將從N型PM函數(shù)(具有2個(gè)非單調(diào)點(diǎn)且單調(diào)區(qū)間由增到減再到增的PM函數(shù))開始,充分利用該函數(shù)的非單調(diào)點(diǎn)在迭代下的變化規(guī)律,確定此類函數(shù)的非單調(diào)高度分類,從而刻畫N型PM函數(shù)的動力學(xué)性質(zhì).

1 準(zhǔn)備知識

下面給出逐段單調(diào)函數(shù)及其相關(guān)的概念.

定義 1.1[8-9](逐段單調(diào)函數(shù)的定義) 假設(shè)F:I→I是連續(xù)映射,c為I的內(nèi)點(diǎn).若F在c的某領(lǐng)域內(nèi)嚴(yán)格單調(diào),則稱c為映射F的單調(diào)點(diǎn);反之,稱c為映射F的非單調(diào)點(diǎn).進(jìn)一步,稱具有有限多個(gè)非單調(diào)點(diǎn)的連續(xù)函數(shù)F:I→I為嚴(yán)格逐段單調(diào)連續(xù)函數(shù)(簡稱PM函數(shù)),記PM(I,I)為區(qū)間I上所有連續(xù)自映射PM函數(shù)全體.

令F∈PM(I,I),定義S(F)為映射F的所有非單調(diào)點(diǎn)集合,N(F)為F的非單調(diào)點(diǎn)個(gè)數(shù),得到下面有用的結(jié)論.

引理1.2[13]令函數(shù)

F:[a,b]→R,G:[p,q]→R

為連續(xù)函數(shù),其中

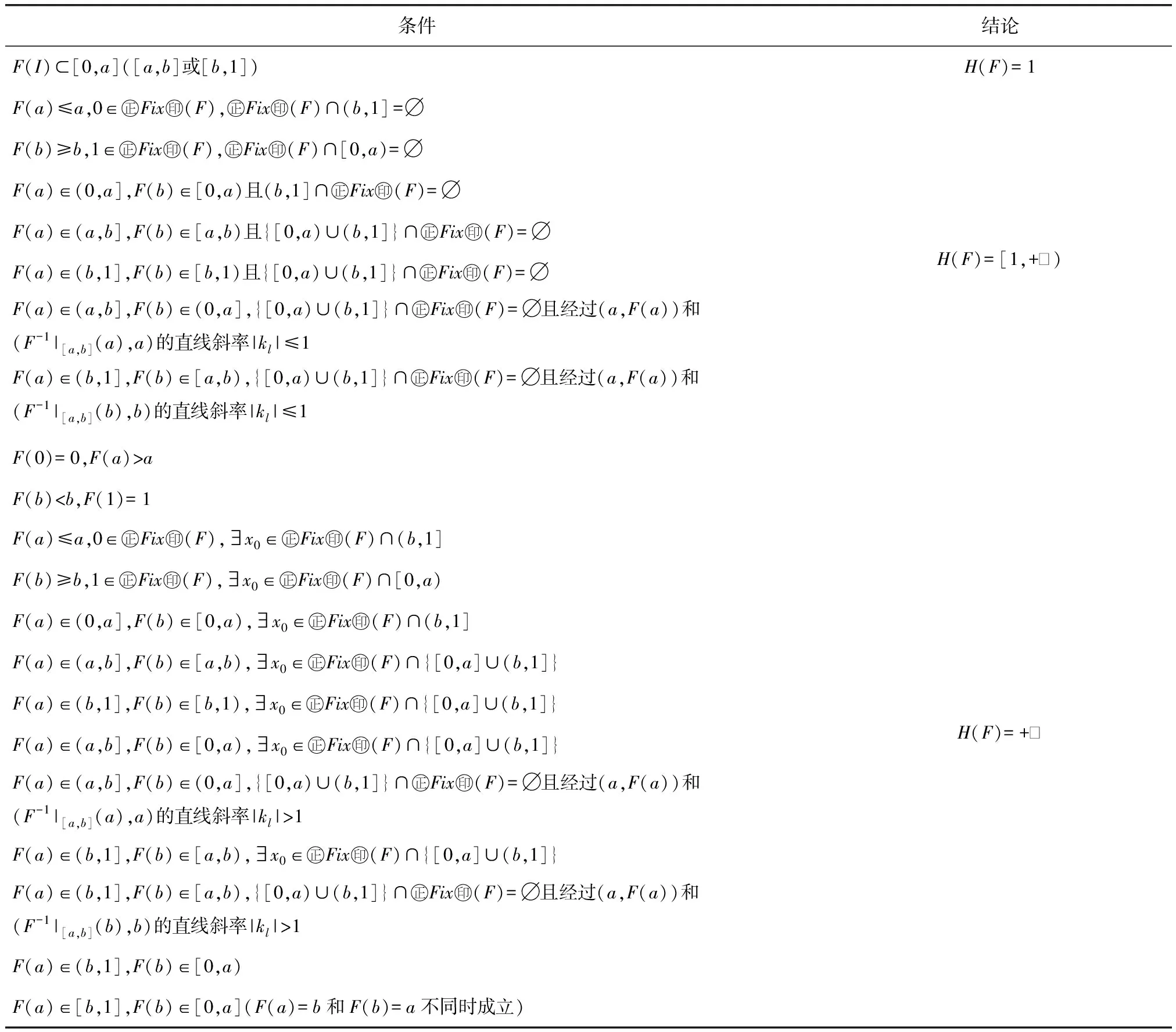
p,q∈R,p

則有

S(G°F)=S(F)∪{c∈(a,b),F(c)∈S(G)}.

顯然,PM函數(shù)在迭代下的非單調(diào)點(diǎn)個(gè)數(shù)是非減的.因此,可以定義PM函數(shù)的非單調(diào)高度.

定義 1.3[13](非單調(diào)高度的定義) 令

F∈PM(I,I),

H(F)為滿足等式

N(Fk)=N(Fk+1)

的最小整數(shù)k,這里的k可以是個(gè)有限數(shù),也可以是無窮,這樣的H(F)稱為F的非單調(diào)高度(或簡稱為高度).

根據(jù)非單調(diào)高度的定義,可以得到以下等價(jià)條件.

定義 1.4[9-10](特征區(qū)間的定義) 假設(shè)

H(F)=1,

那么F在某個(gè)區(qū)間[p,q]上是嚴(yán)格單調(diào)的,其中

p=minF,q=maxF.

適當(dāng)?shù)財(cái)U(kuò)充F的單調(diào)區(qū)間,可以找到2個(gè)點(diǎn)

a′,b′∈I,a′

使得:

(i)a′和b′是非單調(diào)點(diǎn)或端點(diǎn);

(ii) (a′,b′)內(nèi)沒有非單調(diào)點(diǎn);

(iii) [a′,b′]?[p,q].

以上獲得的唯一區(qū)間[a′,b′]被稱為F的特征區(qū)間.

利用上述的非單調(diào)高度和特征區(qū)間的定義,討論N型PM函數(shù)的高度分類.為了方便起見,不妨令I(lǐng)為單位區(qū)間,即I=[0,1],其中a和b為N型PM函數(shù)的2個(gè)非單調(diào)點(diǎn).

首先,引入下列有用的結(jié)果.

定理 1.5[17]令函數(shù)

F∈PM(I,I),

若存在子區(qū)間I′?I使得

I′?F(I′)

且

S(F)∩intI′≠?,

則有

H(F)=+∞.

特別地,當(dāng)F(I)=I時(shí),有

H(F)=+∞,

其中intI′表示I′的內(nèi)部.

2 主要結(jié)果

利用特征區(qū)間的定義,容易得到下面的結(jié)果.

定理 2.1令函數(shù)

F∈PM(I,I),

當(dāng)F(I)?[0,a]([a,b]或[b,1])時(shí),則

H(F)=1.

事實(shí)上,這里F的特征區(qū)間為[a,b].

定理 2.2令函數(shù)

F∈PM(I,I),

若

F(0)=0,F(a)>a,

則有

H(F)=+∞.

證明當(dāng)

F(0)=0,F(a)>a,

根據(jù)F的連續(xù)性可知,存在點(diǎn)c1∈(0,a)使得F(c1)=a,其中c1是F2的非單調(diào)點(diǎn).由于

F(0)=0,F(c1)=a>c1,

于是存在點(diǎn)c2∈(0,c1)使得F(c2)=c1,其中c2是F3的非單調(diào)點(diǎn).進(jìn)而可推斷出,存在一個(gè)嚴(yán)格單調(diào)遞減的數(shù)列{cn},n=1,2,3,…使得因此,根據(jù)非單調(diào)高度的定義,可以得到

H(F)=+∞.

證畢.

推論 2.3令函數(shù)

F∈PM(I,I),

若

F(b)

則有

H(F)=+∞.

為了方便定理的闡述,令Fix(F)為F的所有不動點(diǎn)集合.

定理 2.4令函數(shù)

F∈PM(I,I),

若

F(a)≤a, 0∈Fix(F).

若

Fix(F)∩(b,1]≠?,

則有

H(F)=+∞；

若

Fix(F)∩(b,1]=?,

則有

H(F)∈[1,+∞).

證明1) 若Fix(F)∩(b,1]≠?,由0∈Fix(F)以及定理1.5可得H(F)=+∞.

H(F)=1.

假設(shè)F(1)∈(a,1),則存在點(diǎn)c1∈(b,1]使得F(c1)=a.由F的連續(xù)性可知,存在點(diǎn)c2∈(c1,1]使得F(c2)=c1.這里可以得到一個(gè)單調(diào)遞增數(shù)列{cn}.又因?yàn)镕(1)<1,所以數(shù)列中元素僅有有限個(gè),即H(F)為有限值,于是

H(F)∈[1,+∞).

證畢.

推論 2.5令函數(shù)

F∈PM(I,I),F(b)≥b, 1∈Fix(F),

若

Fix(F)∩[0,a)≠?,

則有

H(F)=+∞；

若

Fix(F)∩[0,a)=?,

則有

H(F)∈[1,+∞).

定理 2.6令函數(shù)

F∈PM(I,I),

其中

F(a)∈(0,a], F(b)∈[0,a).

若

Fix(F)∩(b,1]≠?,

則有

H(F)=+∞；

若

Fix(F)∩(b,1]=?,

則有

H(F)∈[1,+∞).

證明1) 若Fix(F)∩(b,1]≠?,由于F(b)

2) 若Fix(F)∩(b,1]=?,若F(1)≤a,F(I)?[0,a],由特征區(qū)間的定義直接得出

H(F)=1.

假設(shè)F(1)∈(a,1),則由介值性定理可知,存在點(diǎn)c1∈(b,1]使得F(c1)=a.又由F的連續(xù)性可知,存在點(diǎn)c2∈(c1,1]使得F(c2)=c1.這里產(chǎn)生了一個(gè)單調(diào)遞增數(shù)列{cn},n=1,2,3,….因?yàn)镕(1)<1,所以數(shù)列中元素僅有有限個(gè),即得H(F)為有限值.于是,可知H(F)∈[1,+∞).證畢.

推論 2.7令函數(shù)

F∈PM(I,I),

其中

F(a)∈(a,b],F(b)∈[a,b).

若

{[0,a)∪(b,1]}∩Fix(F)≠?,

則有

H(F)=+∞；

若

{[0,a)∪(b,1]}∩Fix(F)=?,

則有

H(F)∈[1,+∞).

推論 2.8令函數(shù)

F∈PM(I,I),

其中

F(a)∈(b,1],F(b)∈[b,1).

若

{[0,a)∪(b,1]}∩Fix(F)≠?,

則有

H(F)=+∞；

若

{[0,a)∪(b,1]}∩Fix(F)=?,

則有

H(F)∈[1,+∞).

定理 2.9令函數(shù)F∈PM(I,I),其中

F(a)∈(a,b],F(b)∈[0,a).

若

{[0,a)∪(b,1]}∩Fix(F)≠?,

則有

H(F)=+∞；

若

{[0,a)∪(b,1]}∩Fix(F)=?,

進(jìn)一步,令l為經(jīng)過(a,F(a))和(F-1|[a,b](a),a)的直線,則當(dāng)|kl|≤1時(shí),有

H(F)∈[1,+∞);

當(dāng)|kl|>1時(shí),有

H(F)=+∞,

其中kl表示直線l的斜率.

證明1) 若{[0,a)∪(b,1]}∩Fix(F)≠?,類似定理2.6的結(jié)論,可知H(F)=+∞；

2) 若{[0,a)∪(b,1]}∩Fix(F)=?,因F(a)>a且F(b)

?c∈(a,b),

使得F(c)=a.

若|kl|<1,則有F(a)-a

若|kl|=1,則有F(a)-a=c-a,即F(a)=c.因此,對?x∈(a,b)都有F(x)≠c,即在區(qū)間(a,b)內(nèi)通過迭代不存在異于a、b的非單調(diào)點(diǎn)產(chǎn)生,再由定理2.6以及推論2.8可得H(F)∈[1,+∞).

若|kl|>1,則有F(a)-a>c-a,即F(a)>c.又由F(c)=a

F(c2)=c1.

再根據(jù)

F(c1)=c>c2,F(c2)=c1

可知,存在點(diǎn)c3∈(c1,c2),使得

F(c3)=c2.

……

于是,這里分別產(chǎn)生了一個(gè)單調(diào)遞增數(shù)列

{c2k+1},k=1,2,…

以及一個(gè)單調(diào)遞減數(shù)列

{c2k},k=1,2,…

并且這2個(gè)數(shù)列都是收斂于F的不動點(diǎn).因此,得到

H(F)=+∞.

證畢.

推論 2.10令函數(shù)

F∈PM(I,I),

{[0,a)∪(b,1]}∩Fix(F)≠?,

則有

H(F)=+∞；

若

{[0,a)∪(b,1]}∩Fix(F)=?,

H(F)∈[1,+∞);

當(dāng)|kl|>1時(shí),有

H(F)=+∞,

其中kl表示直線l的斜率.

定理 2.11令函數(shù)

F∈PM(I,I),

當(dāng)

F(a)∈(b,1],F(b)∈[0,a)

時(shí),有

H(F)=+∞.

證明由F(a)∈(b,1],F(b)∈[0,a)可知,存在點(diǎn)c,d∈(a,b)使得

F(c)=b,F(d)=a.

對于區(qū)間(a,d),記l為經(jīng)過點(diǎn)(a,F(a))、(d,F(d))的直線.由F(a)∈(b,1],F(d)=a可知,|kl|>1,那么由推論2.10可知

H(F)=+∞.

證畢.

推論 2.12令函數(shù)

F∈PM(I,I),

當(dāng)F(a)∈[b,1],F(b)∈[0,a](F(a)=b和F(b)=a不同時(shí)成立)時(shí),則有

H(F)=+∞.

最后,F(a)∈(a,b]，F(xiàn)(b)∈[0,a)且F(0)∈(0,a)以及F(a)∈(b,1],F(b)∈[a,b)且F(1)∈(b,1)這2種情況都可以按照上述的方法討論.

3 結(jié)論

從上述討論可知,對N型PM函數(shù)(增→減→增)所有情況下的非單調(diào)高度已經(jīng)給出完整的結(jié)果,如表1所示.利用此方法,反N型PM函數(shù)(減→增→減)的非單調(diào)高度情況也可以類似討論.由于本文只討論2個(gè)非單調(diào)點(diǎn)的情況,那么對于有限多個(gè)非單調(diào)點(diǎn)函數(shù)的非單調(diào)高度該如何去討論呢？這將是接下來要繼續(xù)研究的問題.

表 1 不同條件下的非單調(diào)高度

致謝國家級大學(xué)生創(chuàng)新創(chuàng)業(yè)訓(xùn)練計(jì)劃項(xiàng)目(202110354039)對本文給予了資助，謹(jǐn)致謝意.