方程φe(n)=2ω(n)(e=8,12)的正整數(shù)解
余 禮, 廖群英
(四川師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 四川 成都 610066)
1 引言及主要結(jié)果
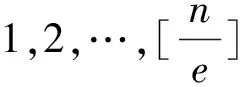
由廣義歐拉函數(shù)的定義易知
φ1(n)=φ(n)
且
近年來,Cai等[3-4]利用勒讓德符號(hào)和雅可比符號(hào)得到了φe(n)(e=3,4,6)的準(zhǔn)確計(jì)算公式.最近,Yang等[5]得到了廣義歐拉函數(shù)φe(n)(e=8,12)的準(zhǔn)確計(jì)算公式.此外,許多學(xué)者對(duì)歐拉函數(shù)和廣義歐拉函數(shù)的相關(guān)方程進(jìn)行了研究.例如:文獻(xiàn)[6-9]用初等方法研究了e∈{1,2,3,4,6}時(shí),方程
φe(n)=2ω(n)
的可解性,并給出了全部正整數(shù)解,其中ω(n)定義為n的所有不同素因子的個(gè)數(shù),ω(1)=0;金明艷等[10]完全確定了方程
φ2(n)=2Ω(n)
的正整數(shù)解,其中Ω(n)定義為n的所有素因子的個(gè)數(shù)(按重?cái)?shù)算),Ω(1)=0;鄧桂林等[11]研究了方程
φe(n)=2tω(n),e=2,3,4,6
的可解性,給出了其部分正整數(shù)解.
本文利用初等的方法和技巧,完全確定了方程φe(n)=2ω(n)在e=8,12時(shí)的全部正整數(shù)解,即證明如下2個(gè)主要結(jié)果.
定理 1.1方程
φ8(n)=2ω(n)
(1)
的全部正整數(shù)解為
n=17,19,23,27,32,35,51,58,62,68,80,
96,154,182,186,170,204,228,240.
定理 1.2方程
φ12(n)=2ω(n)
(2)
的全部正整數(shù)解為
n=25,27,29,31,55,63,65,69,86,88,92,94,
104,106,112,144,195,230,238,260,266,280,
282,306,312,336,342,360,714,780,840.
2 相關(guān)引理
為證明本文主要結(jié)果,需要以下幾個(gè)引理.
引理 2.1[5]若n=2α,α>0,則
引理 2.2[5]若
n=2
其中pi(1≤i≤k)是不同的奇素?cái)?shù).記
Pk={p1,p2,…,pk},
RPk={ri|pi≡ri(mod8),
0≤ri≤7,1≤i≤k},
則
φ8(n)=
引理 2.3[5]若
n=2α3β≥12,
則
引理 2.4[5]若
n=2α3
其中pi(1≤i≤k)是不同的奇素?cái)?shù)且
gcd(pi,6)=1, 1≤i≤k.
記
Pk={p1,p2,…,pk},

0≤ri≤11,1≤i≤k},
則
φ12(n)=
3 主要結(jié)果證明
定理1.1的證明容易驗(yàn)證,當(dāng)n≤8時(shí),均不是方程(1)的解.下面討論n>8時(shí),方程(1)的解的情況.
情形 1若n=2α>8,由引理2.1,方程(1)即為φ8(n)=2α-4=2,解得α=5,此時(shí)n=32.

(Ⅰ) 當(dāng)α∈{0,1},RPk={5,7},{5}時(shí),由引理2.2,方程(1)即為
(3)
1)α=0.由(3)式有
即
若Ω(n)為奇數(shù),則

若Ω(n)為偶數(shù),則
因?yàn)?=2·3,所以k=2,并且α1=α2=1,于是
此式有解
p1=5,p2=7,
所以方程(1)有解n=35.
2)α=1.由(3)式有
即
若Ω(n)為奇數(shù),則
因?yàn)?8=2·32,所以k=2,α1=α2=1,于是
此式有解p1=7,p2=13,則方程(1)有解n=182;
若Ω(n)為偶數(shù),則
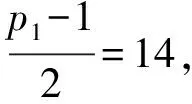
(Ⅱ) 當(dāng)α∈{0,1,2},RPk={3,7},{3}時(shí),由引理2.2,方程(1)即為
(4)
1)α=0.由(4)式有
即
若Ω(n)為奇數(shù),則
有解k=1,α1=1,p1=19和k=1,α1=3,p1=3,則方程(1)有解n=19,27;
若Ω(n)為偶數(shù),則
有解k=2,α1=α2=1,p1=3,p2=15,這與p2為奇素?cái)?shù)矛盾,所以方程(1)無解.
2)α=1.由(4)式有
即
若Ω(n)為奇數(shù),則
有解k=2,α1=α2=1,p1=7,p2=11和k=2,α1=α2=1,p1=3,p2=31,則方程(1)有解n=154,186;
若Ω(n)為偶數(shù),則
有解k=1,α1=1,p1=35,這與p1為奇素?cái)?shù)矛盾,所以方程(1)無解.
3)α=2.由(4)式有
即
若Ω(n)為奇數(shù),則
有解k=1,α1=1,p1=15,這與p1為奇素?cái)?shù)矛盾,所以方程(1)無解;
若Ω(n)為偶數(shù),則
有解k=2,α1=α2=1,p1=3,p2=19,則方程(1)有解n=228.
(Ⅲ) 當(dāng)α∈{0,1,2},RPk={7}時(shí),由引理2.2,方程(1)即為
(5)
1)α=0.由(5)式有
即
若Ω(n)為奇數(shù),則
有解k=1,α1=1,p1=23,則方程(1)有解n=23;
若Ω(n)為偶數(shù),則
有解k=2,α1=α2=1,p1=3,p2=11,此時(shí)與RPk={7}矛盾,所以方程(1)無解.
2)α=1.由(5)式有
即
若Ω(n)為奇數(shù),則
有解k=2,α1=α2=1,p1=3,p2=35,這與p2為奇素?cái)?shù)且RPk={7}矛盾,所以方程(1)無解;
若Ω(n)為偶數(shù),則
有解k=1,α1=1,p1=31,則方程(1)有解n=62.
3)α=2.由(5)式有
即
若Ω(n)為奇數(shù),則
有解k=1,α1=1,p1=15,這與p1為奇素?cái)?shù)矛盾,所以方程(1)無解;
若Ω(n)為偶數(shù),則
有解k=2,α1=α2=1,p1=3,p2=19,這與RPk={7}矛盾,所以方程(1)無解.
(Ⅳ) 其他.方程(1)即為
(6)
1)α=0.(6)式可化為
有解k=1,α1=1,p1=17和k=2,α1=α2=1,p1=3,p2=17,則方程(1)有解為n=17,51.
2)α=1.(6)式可化為
有解k=2,α1=α2=1,p1=5,p2=17時(shí),則方程(1)有解為n=170.
3)α=2.(6)式可化為
有解k=1,α1=1,p1=17和k=2,α1=α2=1,p1=3,p2=17時(shí),則方程(1)有解為n=68,204.
4)α=3.(6)式可化為
有解k=1,α1=1,p1=9,這與p1為奇素?cái)?shù)矛盾,所以方程(1)無解.
5)α=4.(6)式可化為
有解k=1,α1=1,p1=5和k=2,α1=α2=1,p1=3,p2=5,則方程(1)有解n=80,240.
6)α=5.(6)式可化為
有解k=1,α1=1,p1=3,則方程(1)有解n=96.
7)α≥6.(6)式可化為
由25-α<1可知此方程無解,所以方程(1)無解.
這就完成了定理1.1的證明.
定理1.2的證明容易驗(yàn)證,當(dāng)n≤12時(shí),均不是方程(2)的解.下面討論n>12時(shí),方程(2)的解的情況.
情形 1若n=2α3β>12.
(Ⅰ)α∈{0,1}.由引理2.3,方程(2)即為

1)α=0.(7)式可化為
3β-1-3(-1)Ω(n)=12.
當(dāng)Ω(n)為奇數(shù)時(shí),3β-1=9,有解β=3,則方程(2)有解n=27;當(dāng)Ω(n)為偶數(shù)時(shí),3β-1=15,此方程無解,所以方程(2)無解.
2)α=1.(7)式可化為
3β-1-3(-1)Ω(n)=24.
當(dāng)Ω(n)為奇數(shù)時(shí),3β-1=21,此方程無解,所以方程(2)無解;當(dāng)Ω(n)為偶數(shù)時(shí),3β-1=27,此方程無解,所以方程(2)無解.
(Ⅱ)β∈{0,1}.由引理2.3,方程(2)即為

1)β=0.(8)式可化為
2α-1+4(-1)Ω(n)=24.
當(dāng)Ω(n)為奇數(shù)時(shí),2α-1=28,此方程無解,所以方程(2)無解;當(dāng)Ω(n)為偶數(shù)時(shí),2α-1=20,此方程無解,所以方程(2)無解.
2)β=1.(8)式可化為
2α+4(-1)Ω(n)=48.
當(dāng)Ω(n)為奇數(shù)時(shí),2α=52,此方程無解,所以方程(2)無解;當(dāng)Ω(n)為偶數(shù)時(shí),2α=44,此方程無解,所以方程(2)無解.
(Ⅲ)α≥2,β≥2.由引理2.3,方程(2)即為
即
2α3β-1=48,
有解α=4,β=2,則方程(2)有解n=144.
情形 2若
其中pi(1≤i≤k)是滿足p1 (9) 1)α=0,β=0.由(9)式有 即 2)α=1,β=0.由(9)式有 即 k=2,α1=α2=1,p1=7,p2=19, 則方程(2)有解n=266; (10) 1)α=0.由(10)式有 即 k=1,α1=1,p1=7, k=2,α1=α2=1,p1=3,p2=11, 2)α=1.由(10)式有 即 3 k=1,α1=1,p1=15, k=1,α1=1,p1=19, 則方程(2)有解n=342. k=1,α1=2,p1=3 和 k=2,α1=α2=1,p1=3,p2=7, 當(dāng)β≥4時(shí),3(-1)Ω(n)+1=8.當(dāng)Ω(n)為奇數(shù)時(shí),由3β-2>1且gcd(3β-2,7)=1可知此方程無解,所以方程(2)無解;當(dāng)Ω(n)為偶數(shù)時(shí),由且3β-4≥1可知此方程無解,所以方程(2)無解. (11) k=1,α1=1,p1=29, 則方程(2)有解n=29. k=2,α1=α2=1,p1=5,p2=23, 則方程(2)有解n=230; k=2,α1=α2=1,p1=3,p2=27, 這與p2為奇素?cái)?shù)且gcd(pi,6)=1矛盾,所以方程(2)無解. k=2,α1=α2=1,p1=3,p2=27, 這與p2為奇素?cái)?shù)且gcd(pi,6)=1矛盾,所以方程(2)無解. k=1,α1=1,p1=23, 則方程(2)有解n=69. k=1,α1=1,p1=47, 則方程(2)有解n=282; k=2,α1=α2=1,p1=3,p2=51, 這與p2為奇素?cái)?shù)且gcd(pi,6)=1矛盾,所以方程(2)無解. 此時(shí)由等式左邊為奇數(shù),而等式右邊為偶數(shù),可知此方程無解,所以方程(2)無解. (12) 1)α=3,β=0.由(12)式有 k=1,α1=α2=1,p1=3,p2=15, 這與p2為奇素?cái)?shù)且gcd(pi,6)=1矛盾,所以方程(2)無解. k=1,α1=1,p1=11, 則方程(2)有解n=88. 2)α≥4,β=0.由(12)式有 2 此時(shí)由等式左邊為奇數(shù),而等式右邊為偶數(shù),可知此方程無解,所以方程(2)無解. 3)α≥3,β=1.由(12)式有 2 此時(shí)由等式左邊為奇數(shù),而等式右邊為偶數(shù),可知此方程無解,所以方程(2)無解. 即 k=1,α1=1,p1=35, 這與p1為奇素?cái)?shù)矛盾,所以方程(2)無解; 即 k=2,α1=α2=1,p1=3,p2=51, 這與p2為奇素?cái)?shù)且gcd(pi,6)=1矛盾,所以方程(2)無解; (Ⅶ) 其他.由引理2.4,方程(2)即為 (13) 1)α=0,β=0.由(13)式有 有解k=2,α1=α2=1,p1=5,p2=13,則方程(2)有解n=65. 2)α=0,β≥1.由(13)式有 3 3)α=1,β=0.由(13)式有 有解k=2,α1=α2=1,p1=7,p2=17,則方程(2)有解n=238. 4)α=1,β≥1.由(13)式有 3 k=2,α1=α2=1,p1=7,p2=17, 則方程(2)有解n=714; k=1,α1=1,p1=17, 則方程(2)有解n=306; 5)α=2,β=0.由(13)式有 有解k=2,α1=α2=1,p1=5,p2=13,則方程(2)有解n=260. 6)α=2,β≥1.由(13)式有 3 k=2,α1=α2=1,p1=5,p2=13, 則方程(2)有解n=780; k=1,α1=1,p1=9, 這與p1為奇素?cái)?shù)矛盾,所以方程(2)無解; 7)α=3,β=0.由(13)式有 有解 k=1,α1=1,p1=13 和 k=2,α1=α2=1,p1=5,p2=7, 則方程(2)有解n=104,280. 8)α=3,β≥1.由(13)式有 3 k=1,α1=1,p1=13 和 k=2,α1=α2=1,p1=5,p2=7, 則方程(2)有解n=312,840; k=1,α1=1,p1=5, 則方程(2)有解n=360; 9)α=4,β=0.由(13)式有 有解 k=1,α1=1,p1=7, 則方程(2)有解n=112. 10)α=4,β≥1.由(13)式有 3 k=1,α1=1,p1=7, 則方程(2)有解n=336; k=1,α1=1,p1=3, 這與gcd(p1,6)=1矛盾,所以方程(2)無解; 11)α≥5,β=0.由(13)式有 由2α-4>1且 gcd(2α-4,3)=1 可知此方程無解,所以方程(2)無解. 12)α≥5,β≥1.由(13)式有 2α-43 這就完成了定理1.2的證明. 本文基于φe(n)(e=8,12)的準(zhǔn)確計(jì)算公式,對(duì)n進(jìn)行分類討論,利用初等的方法和技巧,研究了當(dāng)e=8,12時(shí),φe(n)=2ω(n)的可解性,完全確定了其正整數(shù)解.在此基礎(chǔ)上,可進(jìn)一步討論關(guān)于廣義歐拉函數(shù)的方程φe(n)=pω(n)的可解性,其中p為奇素?cái)?shù).

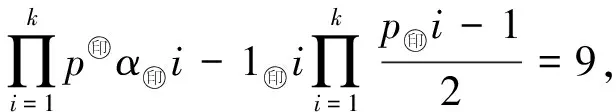





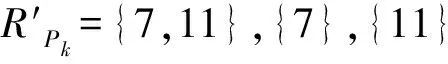




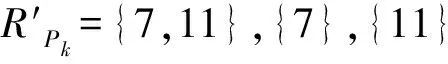




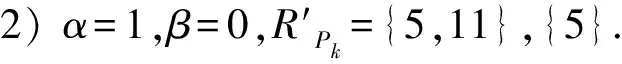
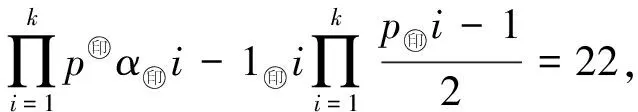

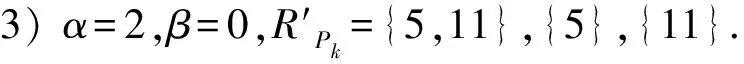
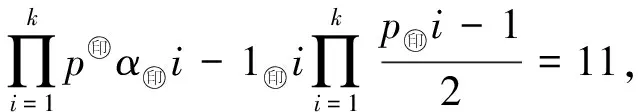
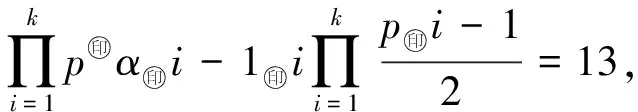

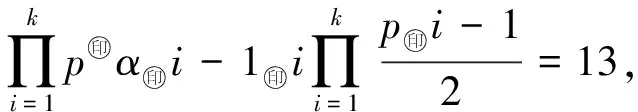
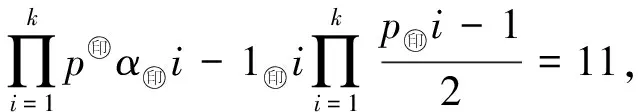
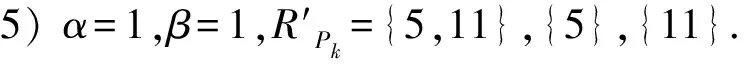







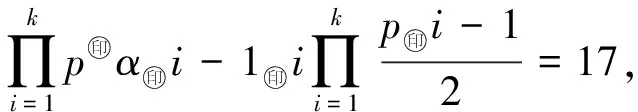





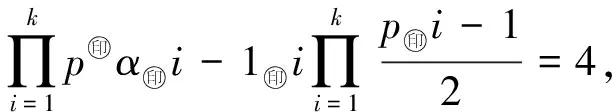

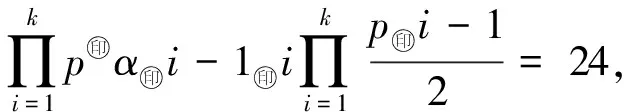










4 小結(jié)與展望

