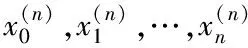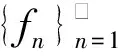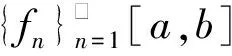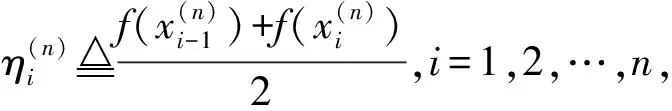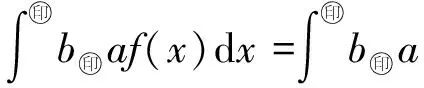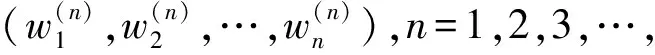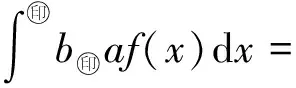Riemann積分和Lebesgue積分的統一性
李洪興
(1. 北京師范大學珠海校區 應用數學學院, 廣東 珠海 519085; 2. 大連理工大學 控制科學與工程學院, 遼寧 大連 116024)
1 關于Riemann積分的定義
考慮一元函數f:[a,b]→R的Riemann積分[1].將閉區間[a,b]做如下的分割:
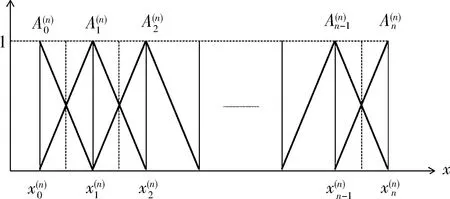
Δ:a=x0 記Δi=[xi-1,xi),i=1,2,…,n-1,以及 Δn=[xn-1,xn];Δxi=xi-xi-1, i=1,2,…,n, 這樣的分割Δ也可以寫成 Δ={Δi|i=1,2,…,n}. 閉區間[a,b]上的全體分割記為Ξ([a,b]). 再記‖Δ‖=叫做分割Δ的模.為了方便,把自然數n叫做分割Δ的分割數;記為n=par(Δ).顯然有‖Δ‖→0?n→+∞,但反之不然. 用C*[a,b]表示[a,b]上幾乎處處連續的有界函數全體,根據函數Riemann可積的充分必要條件可知,C*[a,b]就是[a,b]上Riemann可積的函數全體,即C*[a,b]=R[a,b].在C*[a,b]中引入加法和數乘運算: +:C*[a,b]×C*[a,b]→C*[a,b], (f,g)f+g, ?x∈[a,b], (f+g)(x)=f(x)+g(x); ·:R×C*[a,b]→C*[a,b], (a,f)a·f, ?x∈[a,b], (a·f)(x)=a·f(x), 不難驗證(C*[a,b],+,·)構成一個線性空間.在C*[a,b]中再規定范數: ‖·‖c:C*[a,b]→[0,+∞), f‖f‖c= 那么(C*[a,b],+,·,‖·‖c)就是一個賦范線性空間. 現在任取一個分割 Δ={Δi|i=1,2,…,n}∈Ξ([a,b]), 利用Δ構造定義在閉區間[a,b]上的一組函數: χΔi:[a,b]→{0,1}, xχ i=1,2,…,n, 顯然,{χΔi|i=1,2,…,n}?C*[a,b],并且這組函數在C*[a,b]中是線性無關的.事實上,假定存在一組常數ai∈R,i=1,2,…,n,使得 a1χΔ1+a2χΔ2+…+anχΔn=0, 這里0∈C*[a,b],即0(x)≡0.任取x∈[a,b],則?!i∈{1,2,…,n},x∈Δi,于是 0=a1χΔ1+a2χΔ2+…+anχΔn=aiχΔi. ?i∈{1,2,…,n},ai=0, 記GΔ=span({χΔi|i=1,2,…,n}),表示由{χΔi|i=1,2,…,n}生成的C*[a,b]的n維線性子空間,而{χΔi|i=1,2,…,n}就是該子空間GΔ的基底. 任取ξi∈Δi,i=1,2,…,n,利用函數f得到n個常數f(ξi),i=1,2,…,n;由此構造函數組{χΔi|i=1,2,…,n}的一個線性組合 g ?x∈[a,b],g 根據Riemann積分的定義,當f∈C*[a,b]時,便有 dx= 在Ξ([a,b])上定義等價關系“~”: ?Δ1,Δ2∈Ξ([a,b]), Δ1~Δ2?par(Δ1)=par(Δ2), 由此得到商集[2] 這里[Δ]是Δ所在的等價類.不難看出 這時,對于每一個n=1,2,…,在每個等價類Ξ(n)([a,b])中都取出一個代表元 Δ(n)={Δ(n)i|i=1,2,…,n}, n=1,2,…, ?n,m∈N,n>m?‖Δ(n)‖<‖Δ(m)‖. 由此得到線性子空間序列 GΔ(n)=span({χΔ(n)i|i=1,2,…,n}), n=1,2,3,…. gn?g ?x∈[a,b],g dx= 證明對于任意的ε>0,因為f在[a,b]上連續,所以f在[a,b]上一致連續;于是?x,x′∈[a,b],?δ>0,使得 |x-x′|<δ?|f(x)-f(x′)|<ε. 取N=N(ε)∈N+,使得 ?n∈N+,n>N?‖Δ(n)‖<δ. |gn(x)-f(x)|=|f(ξ(n)i)-f(x)|<ε. 這樣一來,當f∈C[a,b],有 dx= 命題 2如果f∈C*[a,b]并且滿足條件: ?i∈{1,2,…,n},ξ(n)i?A, 證明熟知A?[a,b]為零測集,而f在E=[a,b]A上處處連續.任取x0∈E,對于任意的ε>0,由于f在E上連續,故存在δ>0,使得?x∈E∩(x0-δ,x0+δ),總有 |f(x0)-f(x)|<ε. 取N=N(ε,x0)∈N+,使得 ?n∈N+,n>N?‖Δ(n)‖<δ. |ξ(n)i-x0|≤Δ(n)xi≤‖Δ‖<δ, 所以當n>N時,必有 |gn(x0)-f(x0)|=|f(ξ(n)i)-f(x0)|<ε. 設(X,R,μ)為測度空間[3],取可測集E∈R,滿足μ(E)<+∞,假定f:E→R是有界可測函數,于是?c,d∈R,使得c c=c0 這里Δk=[ck-1,ck),k=1,2,…,n-1,以及 Δn=[cn-1,cn], 即Δ={Δk|k=1,2,…,n},記 ‖Δ‖= Ek={x∈E|f(x)∈Δk}=f-1(Δk), k=1,2,…,n. 如果?s∈R,使得?ε>0,?δ>0,?Δ∈Ξ([c,d]),只要‖Δ‖<δ,便有 |S(Δ)-s|<ε, 即s=則稱函數f在可測集E上關于測度μ是可積的,并把s叫做f在E上關于μ的積分,記作 在Ξ([c,d])上定義等價關系“~”: ?Δ1,Δ2∈Ξ([c,d]), Δ1~Δ2?par(Δ1)=par(Δ2), 由此得到商集 這里[Δ]是Δ所在的等價類.不難看出 這時,對于每一個n=1,2,3,…,在每個等價類Ξ(n)([c,d])中都取出一個代表元: Δ(n)={Δ(n)k|k=1,2,…,n}, n=1,2,3,…, ?n,m∈N,n>m?‖Δ(n)‖<‖Δ(m)‖. 注意到 E(n)k?E(c(n)k-1≤f {x∈[a,b]|f(x)∈[c(n)k-1,c(n)k)}, E(n)n?E(c(n)n-1≤f≤c(n)n)? {x∈[a,b]|f(x)∈[c(n)n-1,c(n)n]}, n=1,2,3,…,k=1,2,…,n-1, 于是 {E(n)k|k=1,2,…,n}= {f-1(Δ(n)k)|k=1,2,…,n}, FΔ(n)=span({χE(n)k|k=1,2,…,n}), n=1,2,3,…. {χE(n)k|k=1,2,…,n} 的一個線性組合: fn?f ?x∈[a,b],f dx= 證明任取σ>0,存在N=N(σ)∈N+,使得?n∈N+,n>N?‖Δ(n)‖<σ.于是 E(|fn-f|>σ)? {x∈E||fn(x)-f(x)|>σ}= 因此,m(E(|fn-f|>σ))=0,這說明 ?x∈[a,b], |fn(x)|≤M. 根據Lebesgue控制收斂定理可知 dx= 答案應該是肯定的.事實上,根據熟知的Lebesgue積分等式: 再利用Lebesgue積分和Riemann積分之間的關系,便有 此外,由Riemann積分等式 還可以得到結論: ddx= 例 1現在用函數逼近論的思想來考察著名的Dirichlet函數的積分: D:[0,1]→{0,1}, x 熟知D?R[0,1],但D∈L[0,1].事實上,Ξ({0,1})={Δ1,Δ2},這里Δ1={0},Δ2={1},注意: E1=D-1(Δ1)=[0,1]∩Qc, E2=D-1(Δ2)=[0,1]∩Q, 顯然{E1,E2}構成區間[0,1]的一個劃分,而{χE1,χE2}是L[0,1]中的一個線性無關組,由此可以生成L[0,1]的一個二維線性子空間H?span({χE1,χE2}).此時,對于積分來講,線性組合系數只有唯一的一種取法:η1=0,η2=1.于是得到線性空間H中的一個元素: h=η1χE1+η2χE2. 不難看出D=h∈H,由此便有 η1·[1·m(E1)]+η2·[1·m(E2)]= η1·m(E1)+η2·m(E2)= 0·1+1·0=0. ddx= {χΔ(n)i|i=1,2,…,n}; gn=f(ξ(n)1)·χΔ(n)1+…+f(ξ(n)n)·χΔ(n)n, GΔ(n)=span({χΔ(n)i|i=1,2,…,n}) 恰好是R[a,b]的n維線性子空間,它對gn封閉.換言之,用有限維線性子空間的元素gn去逼近無限維線性空間R[a,b]的元素f.記G=那么 dim(G)=dim(∞. 這說明gn要想準確地逼近f,任何有限維線性子空間GΔ(n)的元素都是很難做到的.好在R[a,b]的線性子空間G=具有可數基.此外,雖然f,a.e.[a,b],但是極限與積分交換次序,即 ddx 一般不成立.當滿足很強的條件f∈C[a,b]時,f在[a,b]上是一致收斂的,于是成立 dx= fn=η(n)1·χE(n)1+…+η(n)n·χE(n)n, FΔ(n)=span({χE(n)i|i=1,2,…,n}) 恰好是L[a,b]的n維線性子空間,它對fn封閉.換言之,用有限維線性子空間FΔ(n)的元素fn去逼近無限維線性空間L[a,b]的元素f. 記F=那么 dim(F)=dim(∞, dx= 任取函數f∈C[a,b],熟知 對于每一個n=1,2,3,…,在每個等價類Ξ(n)([a,b])中都取出一個代表元: Δ(n)={Δ(n)k|k=1,2,…,n}, n=1,2,3,…, n>m?‖Δ(n)‖<‖Δ(m)‖. 注意到 Δ(n):a=x(n)0 由此構造基函數組[5]如下(見圖1). 圖 1 連續基函數 μ μ i=1,2,…,n-1, μ f(x(n)0),f(x(n)1),…,f(x(n)n), f 可以驗證?i∈{0,1,…,n},有 fn(x(n)i)=f(x(n)i), B(n)i?{f(x(n)i)},i=0,1,…,n, l(n)i(x(n)i-1)=f(x(n)i-1), l(n)i(x(n)i)=f(x(n)i), i=1,2,…,n. L(n) i=1,2,…,n. 事實上,不難知道 L(n)i(x)=f(x(n)i-1)+ i=1,2,…,n, f 證明因為f∈C[a,b],所以f在[a,b]上一致連續.于是,?ε>0,?x,x′∈[a,b],?δ>0,只要|x-x′|<δ,就有 |f(x)-f(x′)|<ε. 取N=N(ε)∈N+,使得 n>N?‖Δ(n)‖<δ. 因為x∈[a,b],所以必有 ?!i∈{1,2,…,n},x∈Δ(n)i, 于是便有 |f(x)-fn(x)|=|f(x)-L(n)i(x)|= |f(x)-f(x(n)i-1)- 此外,令w(n)顯然滿足?i∈{1,2,…,n},必有且 注 2當每個分割 Δ(n):a=x(n)0 為等距分割時,即 Δ(n)i=x(n)i-x(n) i=1,2,…,n, 又有 這究竟是個什么平均數呢?事實上,做如下的變形: 每個 sgn 最后再把積分進一步變形為下列形式: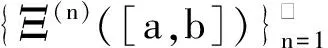

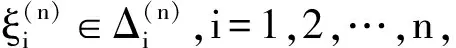
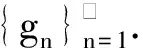
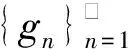

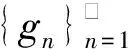
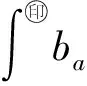
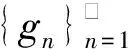

2 關于Lebesgue積分的定義
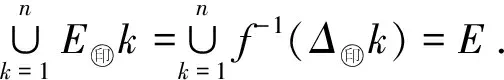


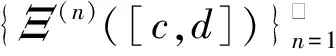


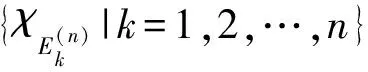

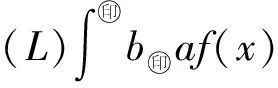
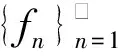
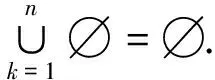
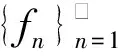
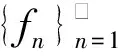
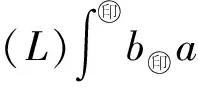
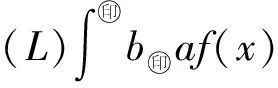
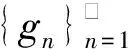

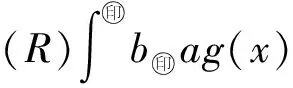

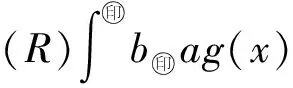
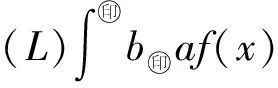
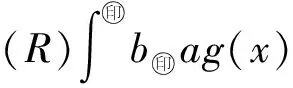
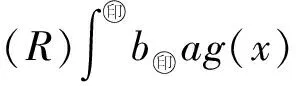
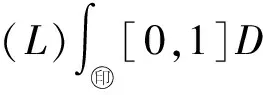



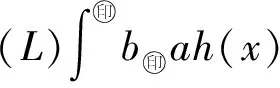
3 關于Riemann積分和Lebesgue積分的統一性
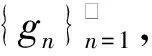



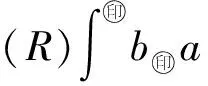
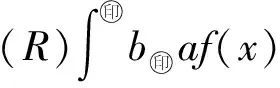
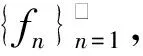
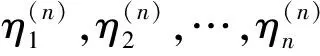
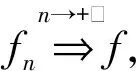
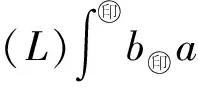
4 連續函數的Riemann積分