基于GA-BP 神經網絡的采空區地表沉降預測模型①

陽 俊， 曾維偉，2

（1.湖南有色金屬職業技術學院，湖南 株洲 412000； 2.中南大學 資源加工與生物工程學院，湖南 長沙 410083）

隨著礦產資源持續開采，不可避免地留下大量地下采空區［1］。 采空區造成的地表沉降或塌陷屬于典型的多因素耦合重大危險源，會對礦山周邊人員和設施構成極大威脅，對社會安定和經濟健康發展產生負面影響［2－3］。 為減少此類事故的發生，有必要對采空區地表沉降進行預測，并根據預測結果及時采取相應的預防措施。

采空區沉降受到地質、采礦參數等多因素影響，且各因素之間存在著模糊且動態的非線性關系，傳統方法很難綜合考慮各種因素的復雜影響并做出準確預測［4］。BP 神經網絡算法［5］具有高度的非線性映射能力，可適用于建立采空區沉降量與主要影響因素之間關系模型，建模過程不需要建立數學方程，可避免傳統采空區沉降預測方法的弊端；但BP 神經網絡具有收斂速度慢以及易陷入局部最優等劣勢。 遺傳算法（Genetic Algorithm，GA）在模型解算時能全局搜索，并能根據短時間內收斂情況確保全局最優解算效果。 本文基于遺傳算法在模型收斂、解算特征等方面的優勢，實現其對BP 神經網絡的改進優化，建立GA-BP 神經網絡采空區地表沉降預測模型，并通過matlab 軟件分別對BP 神經網絡和GA-BP 神經網絡2種模型進行仿真測試，驗證GA-BP 神經網絡模型的預測性能。

1 構建GA-BP 神經網絡預測模型

1.1 GA 優化的BP 神經網絡算法流程

選用GA 優化BP 神經網絡來構建采空區地表沉降演化模型。 模型構建的主要內容包括BP 神經網絡和GA 算法優化兩部分。 BP 神經網絡首先要確定輸入輸出參數個數，然后確定隱含層個數以及節點數，進而確定網絡拓撲結構；GA 算法優化主要利用遺傳學的選擇、交叉和變異原理優化BP 神經網絡的初始權值和閾值；BP 神經網絡再利用GA 算法確保網絡模型設計的初始權值、閾值指標達到最優，然后對模型進行網絡訓練，并更新權值和閾值，最后進行仿真預測。 算法流程如圖1 所示。

圖1 GA 優化BP 神經網絡算法流程

1.2 BP 神經網絡結構

考慮影響采空區地表沉降因素的重要性，選取上覆巖層彈性模量（GPa，X1）、泊松比（X2）、內聚力（MPa，X3）、內摩擦角（（°），X4）、開采深度（m，X5）、采高（m，X6）、礦體傾角（（°），X7）和采場尺寸（×104m2，X8）共8 項指標作為BP 神經網絡的輸入層參數，采空區最大地表沉降量（m，Y）作為輸出層參數。

考慮到模型的運行速率，選擇單隱含層結構。 隱含層節點數對模型預測結果影響很大，目前一般先通過經驗公式計算節點數的可能選擇，然后再通過試湊法選擇預測誤差最小時的隱含層節點數。 經驗公式為［6］：

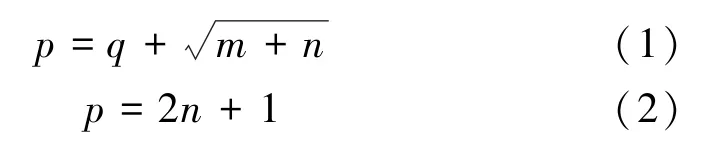
式中p為隱含層節點數；m為輸出層節點數；n為輸入層節點數；q為常數（1≤q≤10）。

由式（1）～（2）計算出隱含層節點數的取值范圍為［4，13］。 根據matlab 軟件仿真結果，當隱含層節點數為10 時，誤差較小。 本文神經網絡隱含層節點數選10。 其網絡結構如圖2 所示。

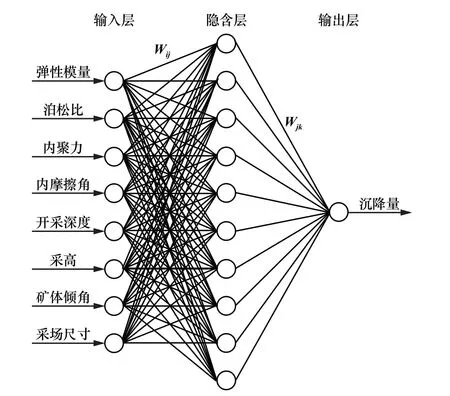
圖2 BP 神經網絡結構

1.3 網絡訓練參數

各層參數見表1。

表1 網絡訓練參數

2 實證分析

2.1 數據來源和歸一化處理

采用參考文獻和礦山現場收集的20 組數據作為模型原始數據［3，7－10］，如表2 所示。

為避免因輸入輸出數據數量級差別太大而導致網絡預測結果不準確，在網絡訓練前采用最大最小法對數據進行歸一化處理，使各指標數據轉化為［0，1］之間的數。 函數形式為［11］：

式中Yk為歸一化處理后的數據；Xk為輸入數據；Xmin為數據序列中的最小數；Xmax為數據序列中的最大數。

根據式（3），利用matlab 軟件對表2 數據進行歸一化處理后的數據如表3 所示。

表2 采空區地面沉降原始數據

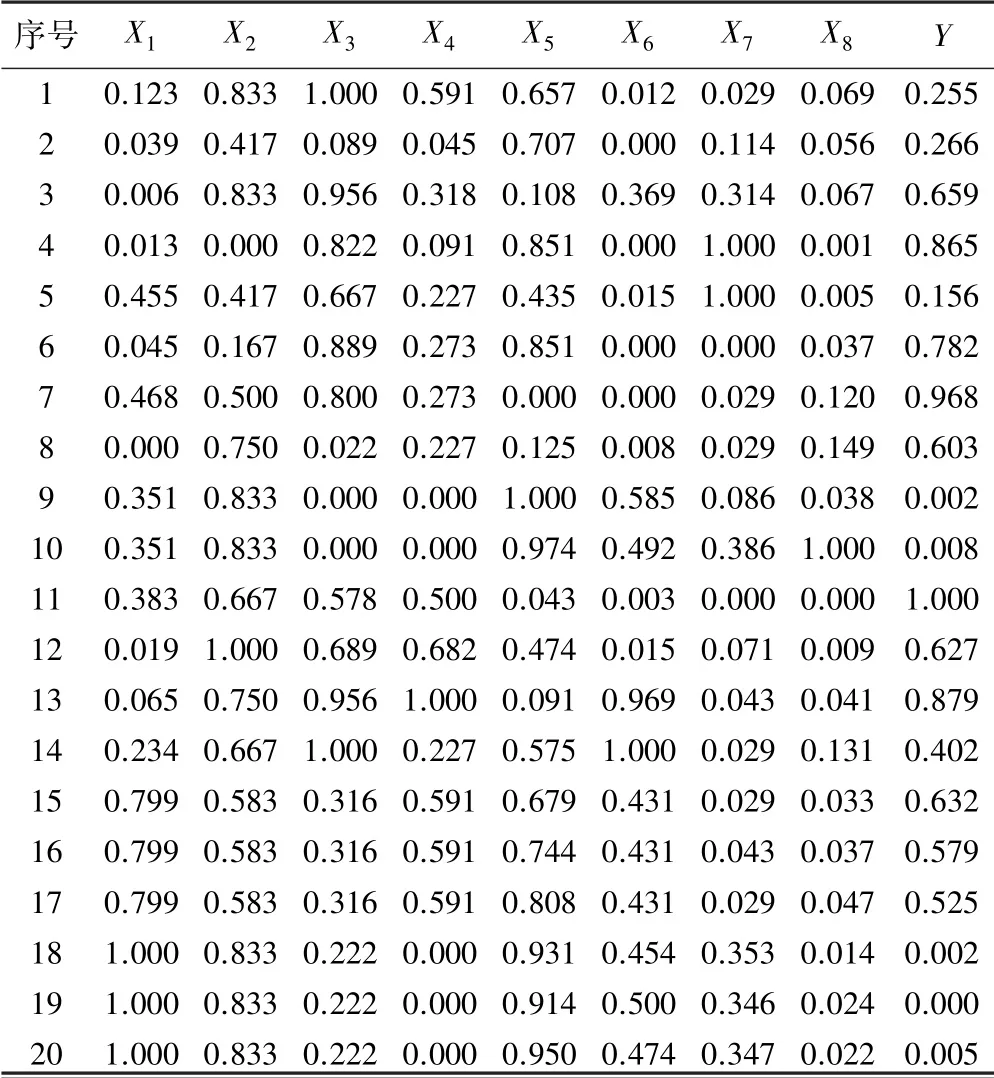
表3 歸一化數據

2.2 網絡模型訓練

利用matlab 軟件中的rand 函數從模型原始數據中隨機選取14 組數據作為網絡訓練參數，并將模型原始數據中的另6 組數據用于網絡測試。 在網絡訓練前，先基于遺傳算法優化BP 神經網絡對應的初始值、閾值參數。 優化后形成的模型適應度曲線變化趨勢見圖3。 在反復對模型進行遺傳優化后，個體適應度指標下降、適應力增強，在進化約37 代時，適應度指標逐漸平穩。 這時就能根據適應度指標演化趨勢來確定網絡的最優初始權值、閾值指標，結果如表4 所示。

圖3 適應度曲線圖

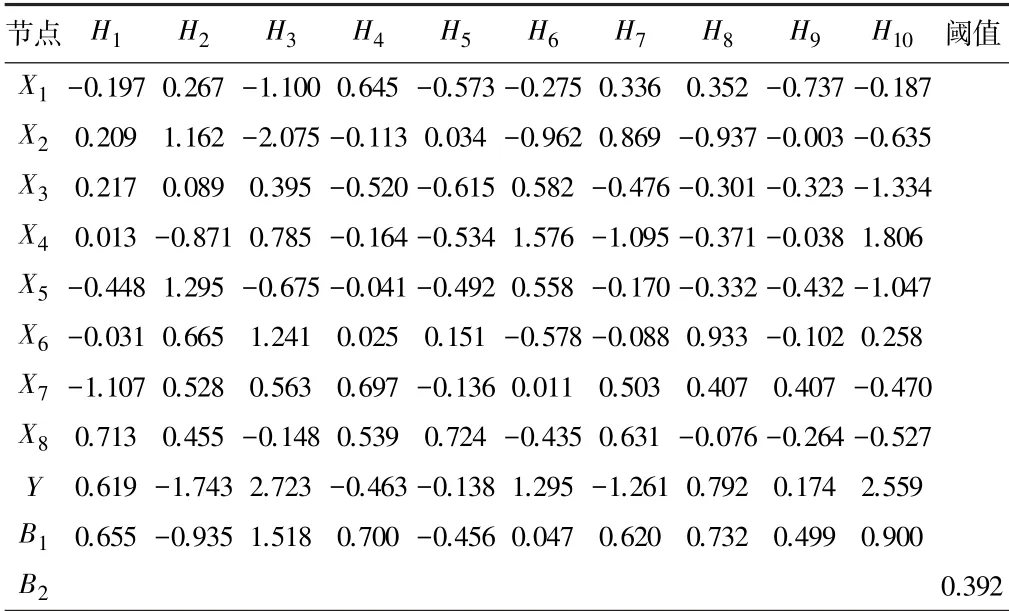
表4 遺傳算法優化后的BP 網絡初始權值和閾值

2.3 模型訓練測試結果分析

結合表1 的網絡參數，對GA-BP 神經網絡訓練后進行系統測試驗證。 為了測試驗證兩種預測模型預測性能的優劣，對傳統BP 網絡模擬測試時，輸入的各項參數、數據樣本等與GA-BP 神經網絡測試時相同。 圖4～5分別為傳統BP 神經網絡和GA-BP 神經網絡的訓練擬合值和真實值對比圖、測試預測值和真實值對比圖。 從圖4～5可知，采用BP 神經網絡和GA-BP 神經網絡對數據進行訓練和預測，訓練點的擬合值和測試點的預測值基本符合真實值，但采用GA-BP 神經網絡的擬合值、預測值與真實值吻合度更高。

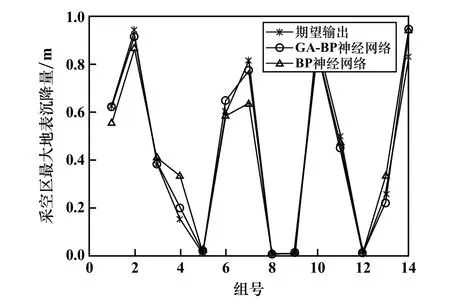
圖4 訓練擬合值和真實值對比結果

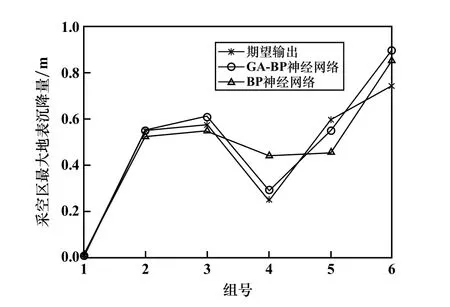
圖5 測試預測值和真實值對比結果

為了更客觀、更科學地對比優化前后2種模型的預測性能，通過均方誤差（Mean Square Error，MSE）、擬合系數R2、收斂速度等指標對模型預測性能進行評價，采用matlab 軟件仿真計算的結果如表5 所示。 結果表明：①GA-BP 神經網絡預測結果的均方誤差小于傳統BP 神經網絡，說明優化后的網絡預測結果更準確；②GA-BP 神經網絡訓練擬合系數R2和測試擬合系數R2都更接近于1，說明優化后的網絡擬合能力更強；③GA-BP 神經網絡收斂速度更快。

表5 網絡模型性能評價指標

3 結論與展望

地下采空區地表沉降預測預警問題是采礦安全領域重要的研究課題。 為了提高采空區地表沉降預測的準確性，本文選擇影響采空區地表沉降的8 項指標進行研究，通過GA-BP 神經網絡構建了采空區地表沉降預測模型，對采空區地表沉降趨勢進行預測與分析。模型解算結果表明，相比傳統BP 神經網絡模型，GA-BP神經網絡的預測精度、數據擬合度及收斂性指標均更高。可見利用GA-BP 神經網絡預測模型進行采空區地表沉降演化趨勢預測有一定可行性，可為采礦領域及其他地下工程項目施工時地表沉降進行預測、預警。但在采礦實踐中，影響采空區沉降的因素還有很多，如地表地形、空區暴露時間、地下水狀況、相鄰空區情況等因素。 綜合采集數據的可獲取因素，用于預測、測試的相關影響指標有一定局限性，測試時搜集的數據樣本相對不足，而一般預測模型都需要大量已知數據作為支撐，小樣本情況下可能導致網絡未能充分訓練，影響網絡預測精度；同時收集到的采空區沉降數據與實際情況也存在一定偏差，使得預測本身帶有不確定性。后續研究應進一步加強與礦山企業合作，以便搜集更多現場實測原始數據樣本，并將該模型用于礦山地表沉降的實際應用驗證；同時可以考慮尋求新的智能算法優化BP 神經網絡，以解決采空區沉降預測中“小樣本、貧信息”問題。