地鐵列車弓網接觸電阻數學模型研究

張冬冬， 李小波， 張 浩， 張 程， 吳竑霖， 汪 翔

（上海工程技術大學 城市軌道交通學院， 上海 201620）

0 引 言

弓網滑動電接觸是地鐵列車獲取電能的途徑，由受電弓和接觸網組成，良好的弓網接觸狀態是確保城市軌道受流質量和安全運行的重要條件之一。 列車運行時，受電弓滑板與接觸線之間的接觸點會形成接觸電阻。 弓網接觸電阻對列車受流質量有較大的影響，同時也影響受電弓滑板與接觸網導線的使用壽命。 接觸點中有少部分絕緣膜會在擊穿電壓下或外力下被破壞，形成導電斑點，導電斑點中有接觸電流流過，由于收縮效應形成收縮電阻，再加上表面膜電阻的和就是接觸電阻。 導電斑點的大小和數目直接影響接觸電阻的大小，導電斑點與接觸元件的材質、接觸形式、接觸力、接觸電流大小等因素密切相關。 弓網接觸狀況與接觸電阻息息相關，因此，接觸電阻的模型計算對改善弓網受流質量及減小磨耗有重要的意義。 陳忠華使用改進的高斯－牛頓迭代算法求解了針對接觸壓力、速度、接觸電流的接觸電阻數學模型；平宇做了波動接觸力下弓網摩擦力建模研究，建立了與波動接觸力和電流相關的模型；時光采用ε 不敏感支持向量機建立波動載荷、接觸電流、滑動速度與接觸電阻之間的預測模型，并采用假設檢驗的方法驗證了模型的有效性；陳忠華從理論上分析了接觸斑點數目的改變對電流穩定性的影響；王鐵軍應用多目標粒子群算法求解電流相對穩定系數和磨損率的Pareto 最優前沿解，通過基于信噪比的多目標決策方法確定基于電流穩定性相對最好、磨損率相對最小情況下的最優壓力載荷；李春茂分析了不同接觸壓力、滑動速度、接觸電流影響下弓網接觸電阻變化趨勢，并根據試驗結果和理論分析建立了接觸電阻數學模型。 目前的研究成果多著眼于電氣化鐵路，對地鐵列車的研究較少，地鐵列車與電氣化鐵路在供電制式、電路拓撲等方面具有很大的不同，本文基于城軌交通受電弓試驗臺測得的數據，通過理論分析建立了符合地鐵運行工況的接觸電阻數學模型，對增強地鐵列車受流可靠性具有重要的參考價值。

1 弓網接觸試驗臺與材料

1.1 試驗臺

本文利用城市軌道交通受電弓試驗系統進行數據采集，如圖1 所示。 受電弓在車輛運行過程中有弓網間的縱向運動、接觸導線的“Z”字形運動、受電弓底座的垂向振動。 縱向運動用一個大直徑的圓盤來模擬，圓盤可以旋轉，接觸網線和弓頭間的彈性接觸，通過彈性懸掛方式模擬，旋轉圓盤運動時通過氣缸推動在導軌上往復運動，模擬“Z”字形運動。

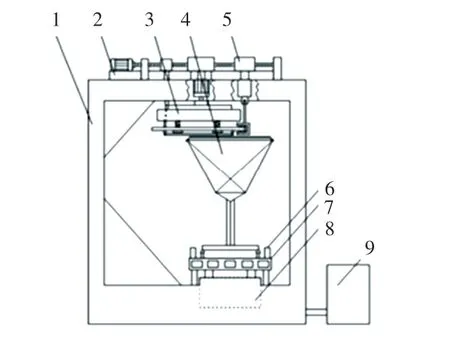
圖1 受電弓試驗臺Fig.1 Pantograph test bench

試驗臺將380 V 三相交流電通過變壓器和整流器變換為50 V 的直流電，輸送給受電弓，利用一個電阻箱模擬車輛負載，如圖2 所示。 為了控制運行和采集性能參數，本系統設置了一套工業計算機和多功能數據采集卡組成的測控系統。 接觸電流、接觸電壓通過回路里的電壓、電流傳感器測量，壓力通過安裝在受電弓兩個滑板兩端的壓力傳感器測得，弓網接觸壓力通過計算其合力得到，接觸電阻通過伏安法計算得到。

圖2 受電弓試驗臺供電和受流系統Fig.2 Power supply and current collection system of pantographtest bench

1.2 試驗材料

試驗中使用的碳滑板參數，見表1；銅錫接觸線參數見表2。

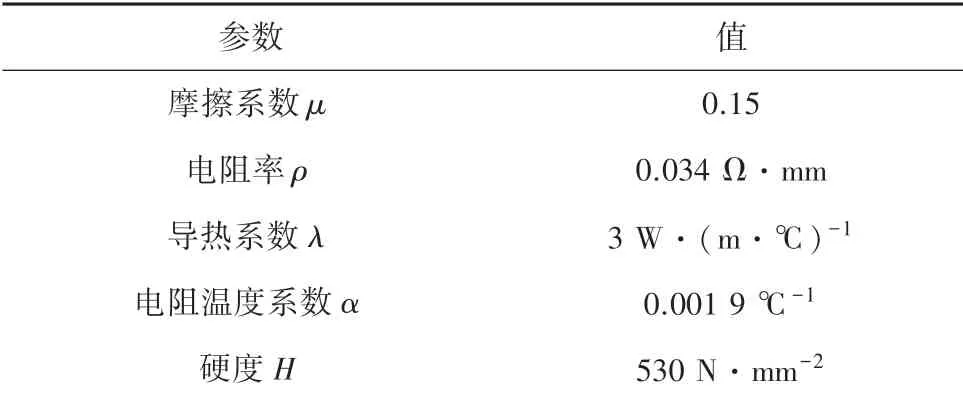
表1 碳滑板參數Tab.1 Carbon skateboard parameters

表2 銅錫接觸線參數Tab.2 Copper tin contact wire parameters

2 試驗結果與分析

2.1 接觸壓力對接觸電阻的影響

當接觸電流為80 A，速度分別為5.55 m／s、8.33 m／s、11.11 m／s 時，得到接觸電阻在接觸壓力為60～120 N 范圍內的變化曲線如圖3 所示。 由圖3 可知，滑動速度與接觸電流不變時，接觸電阻隨接觸壓力的增大而逐漸減小，且接觸電阻減小趨勢逐漸降低。

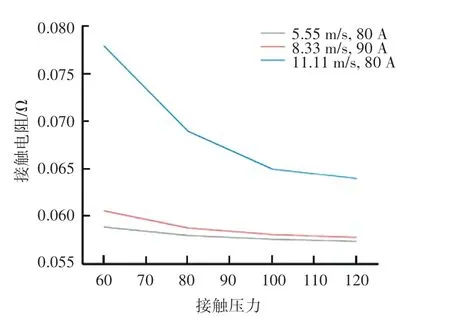
圖3 接觸電阻隨接觸壓力變化曲線Fig.3 Variation curve of contact resistance with contact pressure

根據赫茲彈性接觸理論，弓網接觸的本質是接觸面粗糙不平，形成的微凸峰的接觸，受到的壓力較小時，微凸峰個數也較少，且接觸壓力不足以將大部分表面膜壓破，導電斑點難以形成，阻礙了接觸電流通過，接觸電阻較大；隨著接觸壓力增大，接觸面上較大的微凸峰產生彈性形變，此時較小的微凸峰得以接觸且表面膜被壓破，導電斑點數目增大，接觸電阻減小；壓力繼續增大，較大的微凸峰逐漸在壓力作用下形成塑性形變，接觸面上不再產生新的接觸點，且隨著接觸面積增大，總壓力不再變化，導致每個接觸點的壓強減小，接觸面被刺破的可能性減小，導電斑點數目趨于固定，所以接觸電阻的減小會趨于一個穩定值。

2.2 滑動速度對接觸電阻的影響

當接觸電流為70 A，接觸壓力分別為80 N、100 N；接觸電流為80 A，接觸壓力為100 N 時，得到接觸電阻隨滑動速度在5.55 ～11.11 m／s 之間的變化曲線，如圖4 所示。 由圖4 可知：保持接觸電流和接觸壓力不變時，接觸電阻均隨車輛滑動速度的增大而增大。

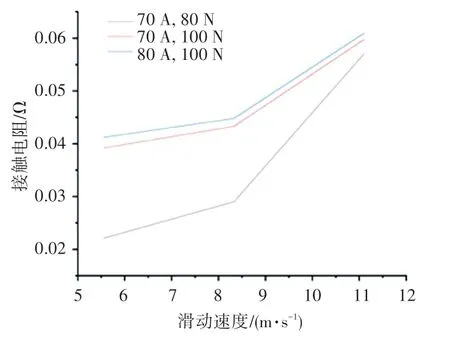
圖4 接觸電阻隨滑動速度變化曲線Fig.4 Change curve of contact resistance with sliding speed

地鐵列車運行過程中速度加快，弓網之間接觸逐漸變得不穩定，導致部分導電斑點消失，從而引起接觸電阻的增大；隨著車輛滑動運行，弓網間機械摩擦會產生大量熱量，使接觸材料變軟，導電斑點接觸面積增大，從而引起接觸電阻減小；隨著接觸不穩定，弓網間產生電弧現象，對接觸面材料造成侵蝕，破壞接觸表面，引起接觸電阻增大。 綜合以上分析，熱量引起的接觸電阻減小相對另外兩點影響較小，所以總體呈現出接觸電阻隨滑動速度增大而增大的趨勢。

2.3 接觸電流對接觸電阻的影響

當滑動速度為8.33 m／s，接觸壓力分別為80 N、100 N、120 N 時，得到接觸電阻隨接觸電流在60～100 A 之間的變化曲線，如圖5 所示。 由圖5 可知，保持滑動速度和接觸壓力不變，隨接觸電流增大，接觸電阻減小，當接觸電流達到90 A 以上后，接觸電阻幾乎穩定。

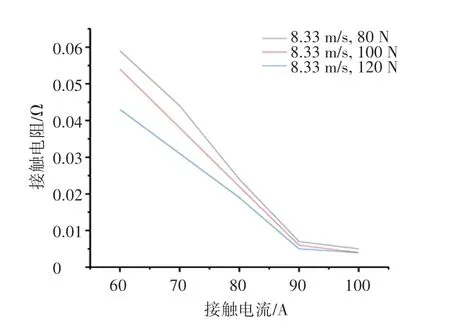
圖5 接觸電阻隨接觸電流變化曲線Fig.5 Change curve of contact resistance with contact current

接觸電流通過接觸面時，會產生大量熱量，引起接觸面硬度的下降，導致導電斑點的半徑、形狀等變大，具體表現就是接觸電阻減小。 同時，隨著接觸電流增大，在接觸表面會形成一層導電性較差的氧化膜，影響了導電斑點的導電性能，導致接觸電阻整體變化趨勢是減小的。 與此同時，接觸電流產生大量的熱量，接觸面溫度會上升，導致接觸電阻減小受到阻礙，減小趨勢變緩，所以在接觸電流達到90A 后，接觸電阻幾乎不再減小。

3 接觸電阻模型的建立與驗證

3.1 模型的建立

3.1.1 接觸電阻關于接觸壓力的模型

單個導電斑點接觸電阻可用公式（1）計算：

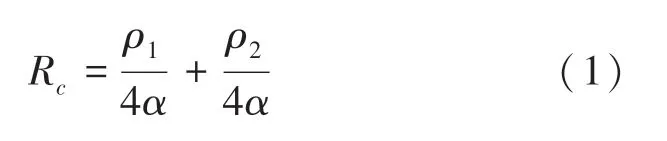
其中，R是單個接觸點的電阻；、分別為兩個接觸面材料電阻率；為接觸點半徑。

假設有個接觸點，且接觸點半徑都相同，可以得到個接觸點的接觸電阻，式（2）：

接觸面半徑與接觸壓力之間的關系可由赫茲公式（3）導出：

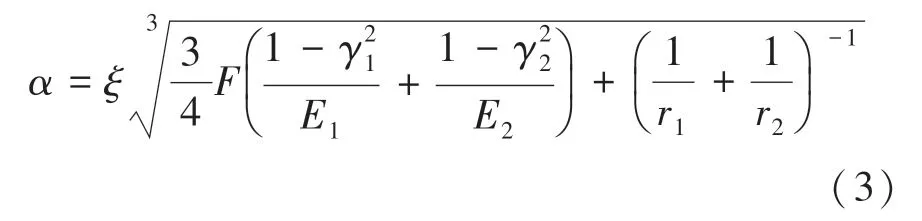
其中，為壓力；為接觸斑點泊松比；為接觸斑點彈性模量；為接觸點半徑；為01 之間的一個修正系數。 整理式（2）、式（3） 得式（4）：

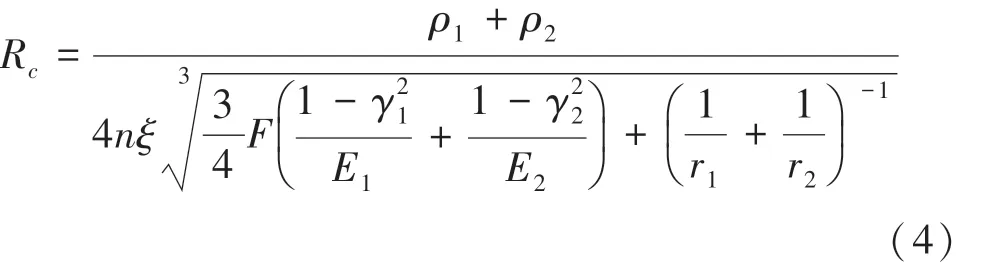
由于泊松比、彈性模量、電阻率、接觸點半徑都屬于常量，所以式（4）可化簡為式（5）：

其中，、為未知參數，為接觸壓力，單位為N。 由于接觸電阻受壓力影響變化最終會趨于一個穩定值，則接觸壓力非常大的時候，摩擦副體電阻就是接觸電阻，此時收縮電阻為0。 因此，考慮在式（5） 中添加一個修正系數，式（6）：

3.1.2 接觸電阻關于接觸電流的模型

已知帶表面膜的接觸電阻可以表示為式（7）：

其中，為未知參數，為接觸面溫升。

由電位－溫度理論可知：導電斑點的接觸溫升與接觸電流有簡單的近似二次函數關系。 所以式（7）轉換為式（8）：

其中，為未知參數。

結合式（6）和式（8）可得弓網接觸電阻關于接觸壓力與接觸電流的模型R，式（9）：

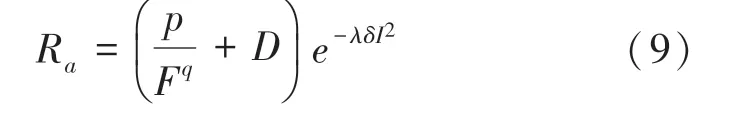
3.1.3 接觸電阻關于滑動速度的模型

由于接觸電阻隨滑動電流變化呈指數性增大，且增大趨勢不受其他因素影響，所以得出接觸電阻關于滑動速度的表達式（10）：

其中，為車輛運行速度；R為靜態接觸電阻，與接觸電流和接觸壓力大小有關；為未知參數。

結合式（9）和式（10）可知，無論速度如何變化，接觸電阻都會隨接觸電流的增大而趨近于0。 由于接觸電阻隨接觸電流增大而趨近于多個不同值，速度越大，這幾個值之間的差距就越大，因此在式（10）后加一個關于速度的多項式來進行修正，式（11）：

其中，、、為未知參數。

結合式（9）～式（11）可得式（12）：

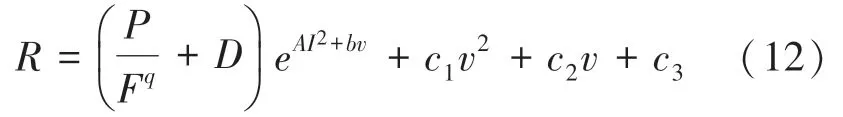
其中，為未知參數，且。

公式（12）即接觸壓力、接觸電流、滑動速度三因素影響下的弓網接觸電阻數學模型。其中、、、、、、、為未知參數，、、為單位為、、的自變量。

3.2 模型的求解與驗證

確定弓網接觸電阻的數學模型后，利用試驗數據對模型的未知參數進行估計，以驗證模型的準確性和有效性。 本文使用1stOpt 軟件對試驗中包含接觸壓力、接觸電流和滑動速度3 個因素的64 組數據點進行非線性擬合。 該軟件使用麥夸特法（Levenberg－Marquardt）和通用全局優化算法（UGO）相結合的迭代算法，實現非線性方程組的求解，特點為全局尋優能力極佳，可以極快地給出最優解，提高求解效率，克服了其他迭代算法必須給出初始值的難題。 表3 為未知參數最優解輸出結果。

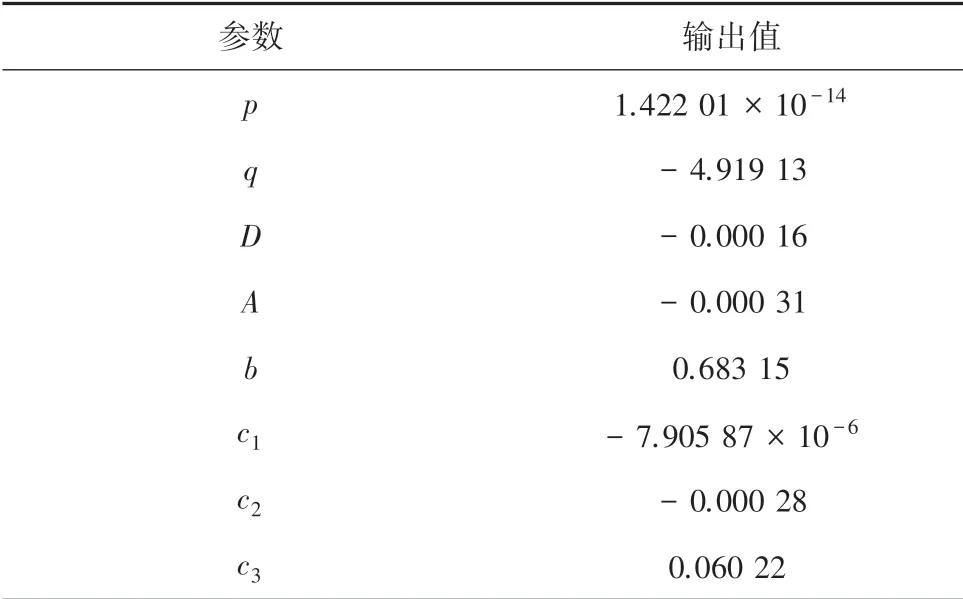
表3 未知參數最優解輸出結果Tab.3 Unknown parameter optimal solution output result

將所求參數代入式（12）得式（13）：

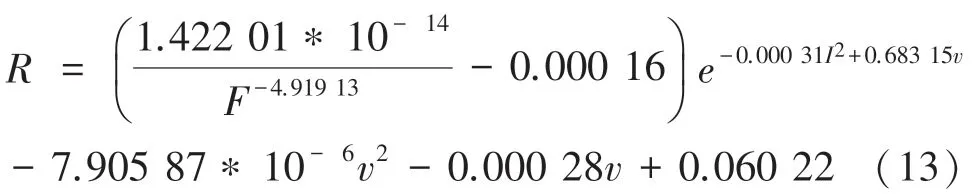
式（13）即為本文所求得的弓網接觸電阻數學模型。

為了驗證模型的有效性，另外選取48 組試驗數據，將這48 個點與相對應的模型計算值比較，如圖6 所示。 由圖6 可知，模型計算值基本分布在試驗測試值附近，兩者吻合度較高，數值上相差不超過0.02 Ω，且試驗值和模型計算值的變化基本趨于一致，說明本文建立的弓網接觸電阻模型是有效的。

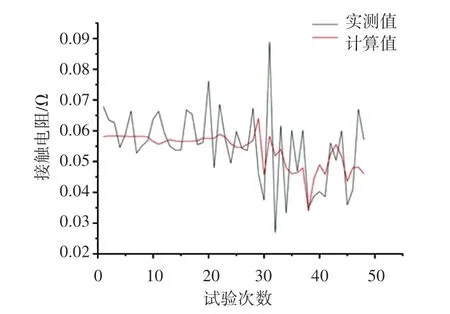
圖6 試驗值與模型計算值對比Fig.6 Comparison of test value and calculated value with model

4 結束語

本文通過試驗數據和理論分析，建立了接觸壓力、接觸電流、滑動速度三因素影響下的地鐵列車弓網接觸電阻數學模型，并驗證了模型的有效性。 通過分析得出如下結論：

（1）當接觸電流和滑動速度不變時，由于接觸壓力導致導電斑點彈性形變，使接觸面積增大，接觸壓力在60 ～120 N 范圍內，接觸電阻隨接觸壓力的增大而減小；

（2）當接觸壓力和接觸電流不變時，滑動速度的增大導致部分導電斑點消失，并且產生電弧，滑動速度在5.55～11.11 m／s 范圍內，接觸電阻隨滑動速度增大而增大；

（3）當接觸壓力和滑動速度不變時，接觸電流的增大產生大量熱量，導致接觸面積增大，接觸電流在60 ～100 A 范圍內，接觸電阻隨接觸電流的增大而減小。

本文的結論為減少地鐵離線現象、增強受流穩定性與可靠性提供了重要參考。