基于隨機森林的汽油精制過程中辛烷值損失模型

薛 潔

（北京信息科技大學 經濟管理學院， 北京 100192）

0 引 言

近年來，隨著汽車尾氣污染問題日趨嚴重，世界各國都制定了嚴格的汽油質量標準。 為此，中國大力發展以催化裂化為核心的重油輕質化工藝技術，對汽油進行精制處理，以實現汽油清潔化。

經研究發現，辛烷值（RON）作為反映汽油燃燒性能最重要的指標，在實現汽油清潔化的過程中，卻不可避免地出現較大的損失值單位。 據統計，RON每降低1 個單位，相當于每噸損失約150 元，這對于一個企業來說，無疑是增加了其生產成本，減少了收益。 以一個100 萬噸／年的催化裂化汽油精制裝置為例，若能降低0.3 個單位的RON 損失，其經濟效益將達到4 500 萬元，因此，降低汽油RON 損失具有重要的意義。

本文以某石化企業為例，研究其RON 損失值的諸多問題。 經廣泛收集各類相關數據，并進行相應處理，綜合運用隨機森林、遺傳算法等統計知識建立并優化相關問題的損失預測模型，利用SPSS（Statistical Product and Service Solutions）、Matlab（Matrix＆laboratory）等軟件對汽油精制過程中的RON 損失進行可視化展示及分析，力求降低其損失值15%以上，增加企業效益。

1 主要變量降維

1.1 建模變量命名

為了方便統計與計算，將所需的354 個操作變量以“M＋變量編號”命名，如1 號位點氫油比命名為“M1”。 同樣，將13 個材料性質以“A＋變量編號”命名，如原料的RON 命名為“A2”，依次據此方式對366 個變量進行命名。

1.2 計算相關性矩陣

因樣本中存在許多特征相同的變量，冗余程度較高，而相關性較強的變量較多會影響隨機森林模型的準確性，使得隨機森林的優勢被削弱；同時，高相關度的屬性會擠占其他屬性被選擇的機會，導致其他具有不同特征信息的屬性無法得到評估，所以在使用隨機森林降維之前， 需對相關度較高的變量進行剔除，以此提高隨機森林的泛化能力。

計算366 個變量的相關性矩陣，按照相關度矩陣的值進行填色。 如圖1 所示， 亮黃色和深藍色表示變量間存在強相關性，本文定義為相關度大于0.8，對于強相關的變量，保留其一即可，刪除冗余變量后，剩余158 個變量，再進行隨機森林的構造，進行再一次降維。

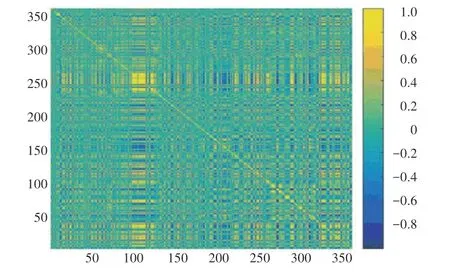
圖1 366 個變量的相關性矩陣Fig.1 Correlation matrix of 366 variables

1.3 隨機森林降維

使用隨機森林算法找出剩余158 個變量的統計結果中信息量最大的特征子集，從而進行降維，重復10 次實驗，對158 個變量的重要程度求平均值后進行排序，得出前30 個主要變量，如圖2 所示。

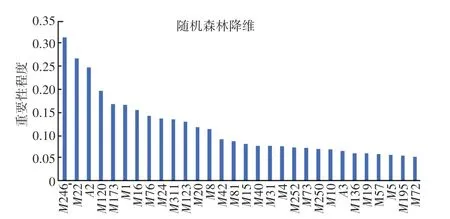
圖2 隨機森林算法計算出前30 個主要變量Fig.2 The first 30 main variables calculated by the random forest algorithm

對前30 個主要變量再次進行篩選，本文保留重要性程度在0.1 以上的主要變量，如圖2 中的2468， 共13 個變量，而后使用SPSS（Statistical Product and Service Solutions）軟件對前6 個變量進行相關性計算，得出表示相關關系強弱情況的皮爾遜相關性與顯著性（雙尾）計算結果，見表1。

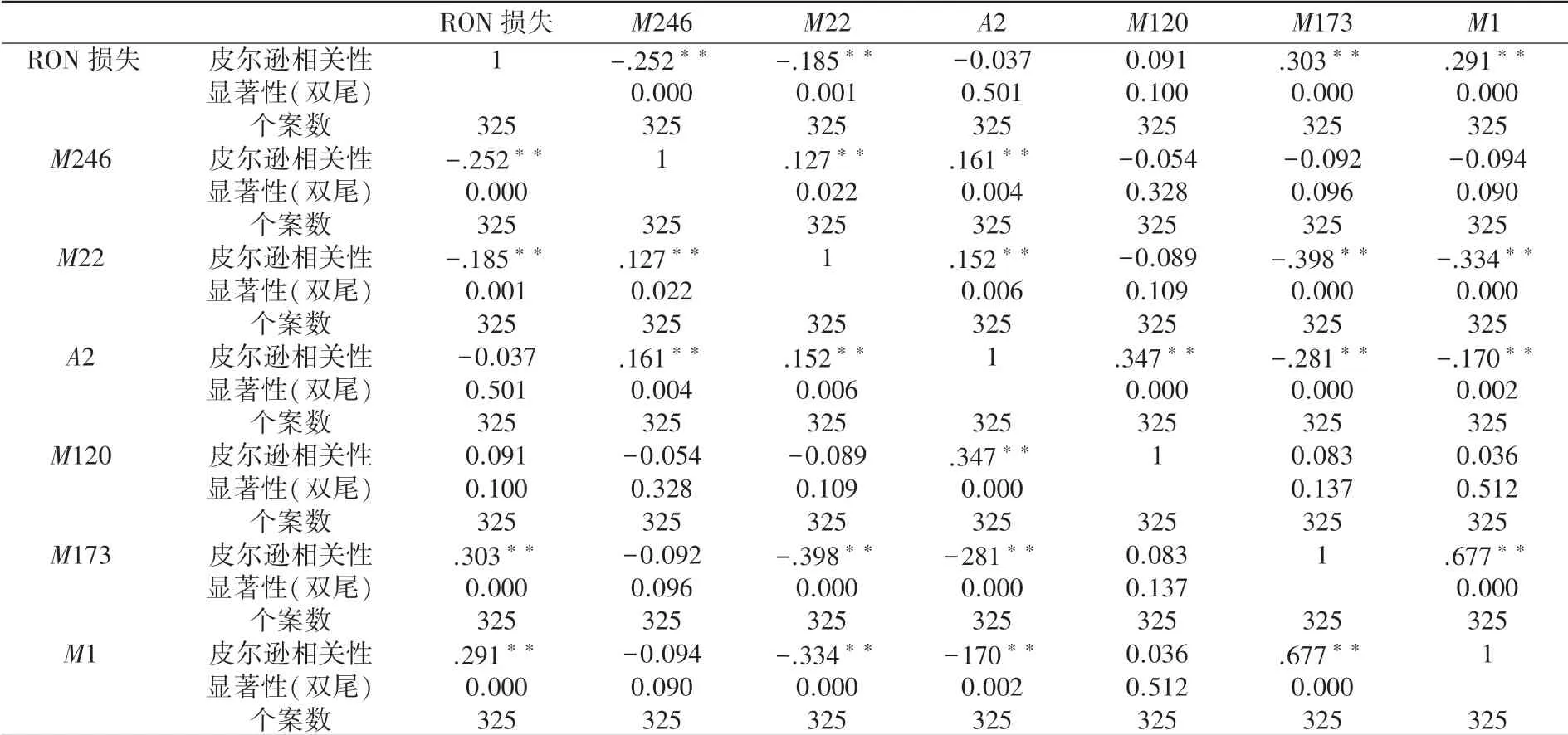
表1 皮爾遜相關性與顯著性（雙尾）計算結果Tab.1 Pearson correlation and significance （two tailed） calculation results

2 基于隨機森林的損失預測模型

2.1 隨機森林預測

隨機森林是一種分類和預測集成的學習算法，其預測模型對部分變量壞值的容忍度較高，能夠更好地利用不同變量與預測值之間的特征信息進行預測。 預測步驟如下：

（1）劃分訓練集與測試集：對原始樣本進行劃分，選出訓練集與測試集。

（2）訓練預測模型：使用帶有輸出的訓練集訓練隨機森林模型。

（3）對測試集進行測試：刪除測試集中的輸出結果，將測試集輸入模型，得到測試集樣本的預測值。

（4）模型評價：對模型預測的誤差進行計算，得到更接進于真實值的最佳測量結果。

2.2 建立RON 損失預測模型

首先對樣本的366 個變量進行處理，刪除冗余變量，保留主要的13 個變量；再將某石化企業的325 個數據樣本以6：4 的比例進行劃分，隨機選出訓練集與測試集；構建隨機森林模型，以訓練集的RON 損失值作為標簽，以13 個主要變量作為特征值輸入訓練模型；最后，將測試集中的13 個變量輸入到訓練好的模型中，得到測試集樣本的預測值，以測試集中預測值與真實值的均方對數誤差作為評價指標，對模型預測的誤差進行計算。 隨機森林模型預測值與真實值曲線對比，如圖3 所示。

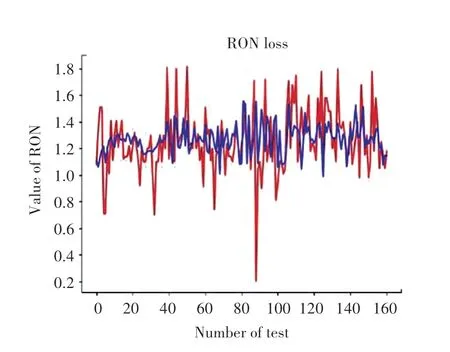
圖3 隨機森林模型預測值與真實值曲線對比圖Fig.3 Comparison of predicted value and true value curve of random forest model

3 基于遺傳算法的優化預測模型

3.1 主要變量操作方案的優化

在13 個主要變量中，除原料的RON 是固定值以外，依次對其他12 個操作變量進行編碼，并在不同取值范圍內進行限幅。 將最大迭代次數設置為100，將預測樣本RON 損失值的倒數作為個體的適應度函數，對325 個數據樣本逐一進行交叉、遺傳、變異、選擇等優化操作；而后運用隨機森林預測模型進行封裝，但個別樣本的適應度在100 次迭代內出現了明顯提高，遺傳算法100 次迭代適應度變化曲線如圖4 所示。 大部分數據無法在迭代內得到優化，效果并不理想，沒有產生降幅大于15%的樣本。

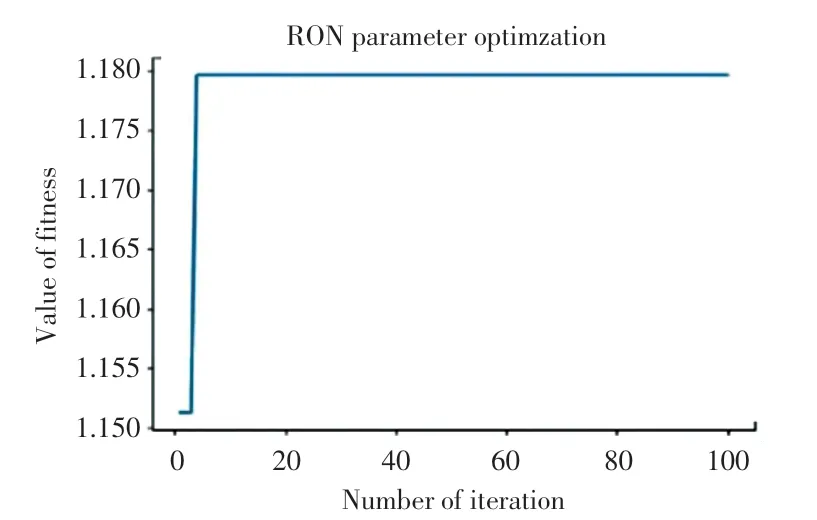
圖4 遺傳算法100 次迭代適應度變化曲線Fig.4 The fitness curve of 100 iterations of genetic algorithm

受計算速度和計算時間的限制，無法對全部數據增加優化的迭代次數，因此只能對小部分樣本進行再一次優化。 如：對129 號樣本在500 次迭代內先后進行2 次優化，迭代適應度變化曲線如圖5所示，其RON 損失值由0.9 降低至0.78，降幅為13.3%，依然沒有產生降幅超過15%的優化數據。

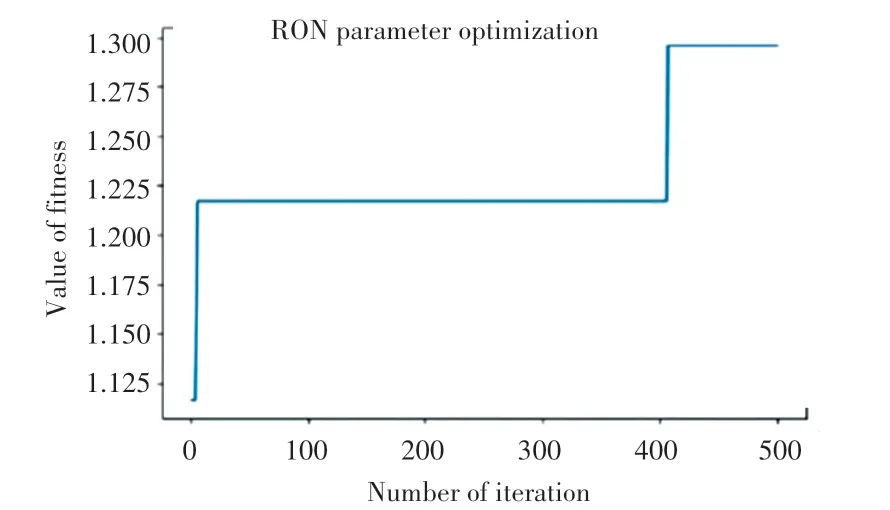
圖5 129 號樣本500 次迭代適應度變化曲線Fig.5 The fitness curve of sample No.129 during 500 iterations

對170 號樣本在1 000 次迭代內先后進行3 次優化，迭代適應度變化曲線如圖6 所示，其RON 損失由0.98 降低至0.81，降幅為17.3%，實現了降幅超過15%的優化目標。

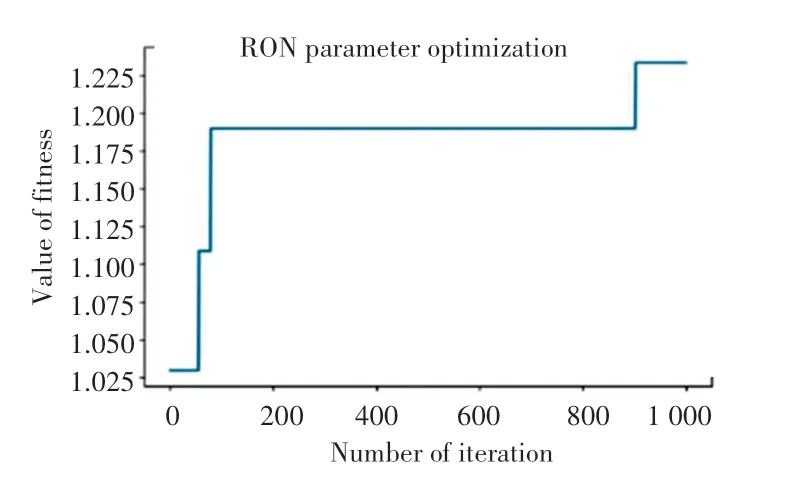
圖6 170 號樣本1 000 次迭代適應度變化曲線Fig.6 The fitness curve of sample No.170 during 1 000 iterations

3.2 優化預測模型的部分可視化展示

為了工業裝置穩定高效運行，優化后的主要變量只能逐步調整到位。 因此，若只改變一種變量，保持其他變量不變，便可得出該變量在優化調整過程中所對應的RON 損失變化軌跡。 以133 號樣本為例，其RON 損失變化曲線如圖7 所示。

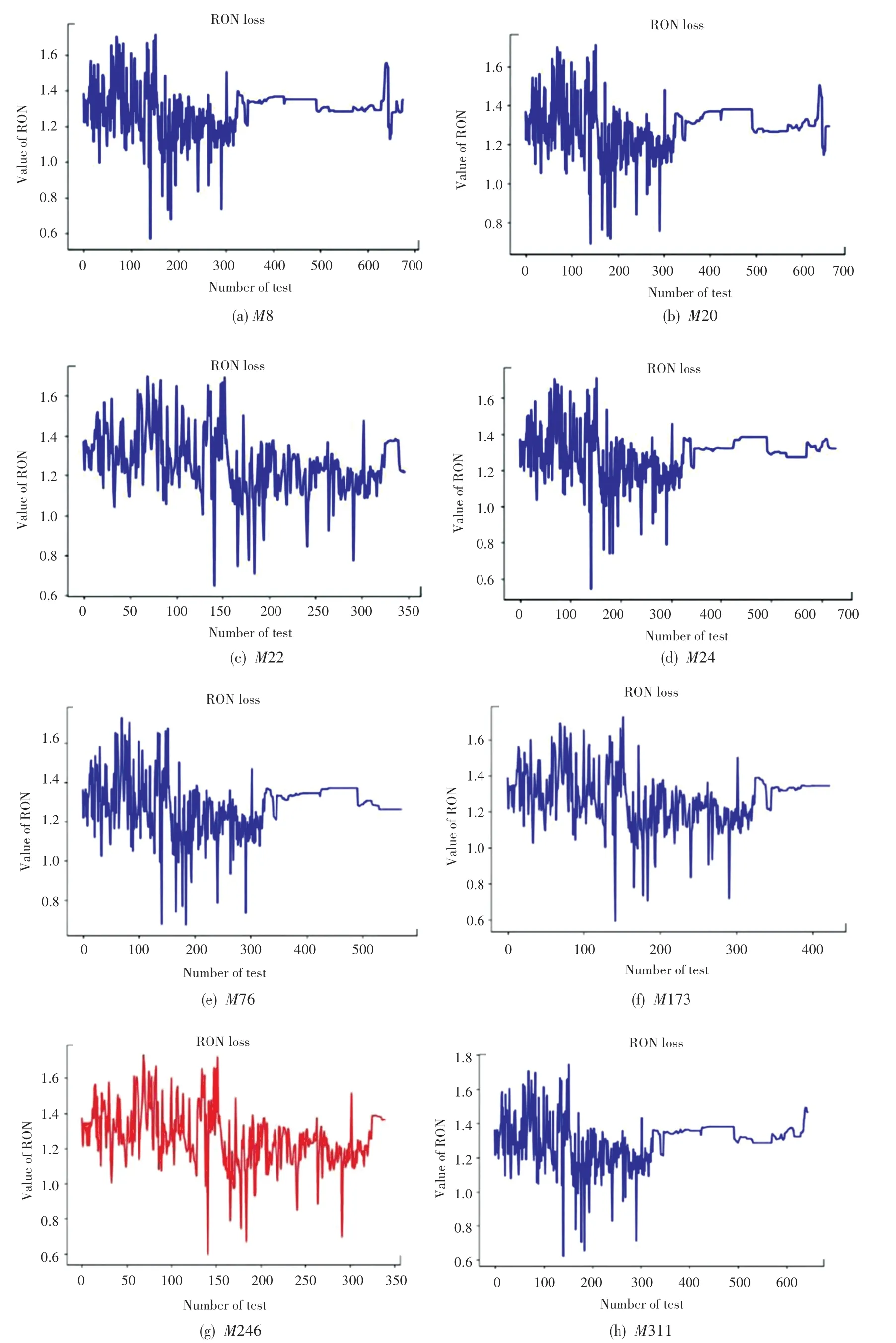
圖7 133 號樣本的RON 損失變化曲線Fig.7 RON loss curve of sample No.133

4 結束語

本文通過對某石化企業原始數據進行處理，將得到預處理后的數據降維，建立基于隨機森林的RON 損失預測模型，對RON 損失及其指標進行預測，通過預測值曲線與真實值曲線的對比，發現其預測結果接近于真實值，說明預測模型有效。

運用遺傳算法優化主要變量，經過多次迭代優化后，最終完成了降幅超過15%的優化目標。 本文基于隨機森林的汽油精制過程中辛烷值損失模型為中國車用汽油質量升級的關鍵技術及其深度開發提供了可靠依據。