基于模糊數學的重大錯報風險評估研究

○廣州民航職業技術學院 徐小燕 李 鋼

《中華人民共和國國家審計準則》(簡稱新審計準則)于2010年9月1日正式頒布，于2011年1月1日起正式實施。新審計準則借鑒了國際審計準則對審計風險的定義，提出審計風險是財務報表存在重大錯報而審計人員發表不適當審計意見的可能性。新審計準則規定，在計劃和實施審計工作時，注冊會計師應當保持職業懷疑，認識到可能存在導致財務報表發生重大錯報的情形。《中國注冊會計師審計準則第1211號——了解被審計單位及其環境并評估重大錯報風險》作為專門規范風險評估的準則，規定注冊會計師應當了解被審計單位及其環境，以充分識別和評估財務報表重大錯報風險，設計和實施進一步的審計程序。只有在充分了解被審計單位及其環境的基礎上，注冊會計師才能評估被審計單位的重大錯報風險。在實務上，多是要求注冊會計師運用實際經驗和職業判斷得出一個定性的評價，但不夠客觀。基于此，本文引入模糊數學的方法，將定量與定性方法結合運用于被審計單位的重大錯報風險評估之中。

一、重大錯報風險評估模型的建立

(一)模糊綜合評價法的概念

模糊綜合評價法是借助模糊數學的基本概念，為實際綜合評價問題提供測度方法。具體來講，模糊綜合評價法就是以模糊數學為基礎，應用模糊關系合成原理，將一些邊界不清、不易定量的因素定量化，從多個因素對被評價事物隸屬等級狀況進行綜合性評判[1]。模糊綜合評價法是基于評價過程的非線性特點而提出的，利用了模糊數學中的模糊運算法則，對非線性的評價等級論域進行綜合量化，從而得到可比的、量化評價結果的過程。由于模糊方法更接近于東方人的思維習慣和描述方法，所以這種模型應用廣泛，采用模糊綜合評價法構建的實用模型已經取得了很好的經濟效益和社會效益。

(二)重大錯報風險評估的具體步驟

1.建立因素集

設X為一級因素集：X={X1,X2, …,X5}，Xi為二級因素集：Xi={Xi1,Xi2,…,Xik}，k為二級指標因素的個數。

本文根據《中國注冊會計師審計準則第1211號——了解被審計單位及其環境并評估重大錯報風險》對了解被審計單位及其環境的總體要求，將影響被審計單位重大錯報風險的因素分為以下8個一級指標，42個二級指標，如表1所示。

2.建立評語集

評語集是評價者對評價對象可能做出的各種評價結果的組成集合。設評語集用W={W1,W2,…,Wm}表示，式中Wi(i=1, 2,…,m)表示由高到低的各級評語。本文結合各個目標實際情況將Wi表示為={低風險,較低風險,一般風險,較高風險,高風險}。

3.建立模糊關系矩陣

設定Ri=(ri1,ri2,…,rin) (i=1,2,3,…,m)。采取類似民意測驗的方法，請行業內專業人士對目標企業的各個目標按上面的評語集進行投票。認為目標ui屬于n個等級v1,v2,…,vj…vn的人數分別為ei1,ei2,…,ein。

假設有20個人參與投票則：Ri=(ri1,ri2,…,rin)=(ei1/20,ei2/20,…,ein/20)，對u1至um共建立m個單因素模糊評判向量：R1,R2,R3,…,Rm。

在審計實務工作中進行重大風險評估時，可以由項目組中的成員對影響被審計單位重大錯報風險的每一個因素進行評價，然后對意見進行匯總。本例中由20位注冊會計師對該大型制造企業重大錯報風險進行評估，得到單因素模糊評價的匯總結果見表2。

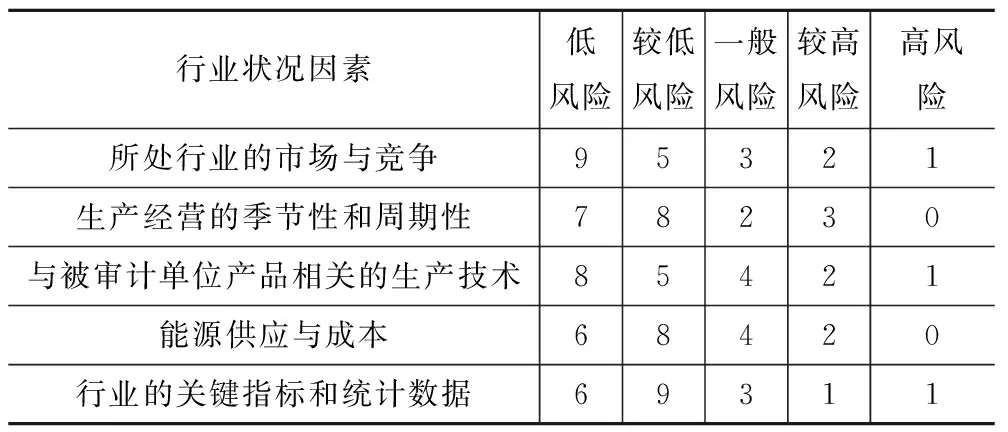
表2 行業狀況調查表

表2中的第一行數字表明，就行業狀況因素而言，評估團20人中有9人認為所處行業的市場與競爭對企業重大錯報風險影響低、5人認為較低、3人認為一般、2人認為較高、1人認為風險高。其它各行依此類推。

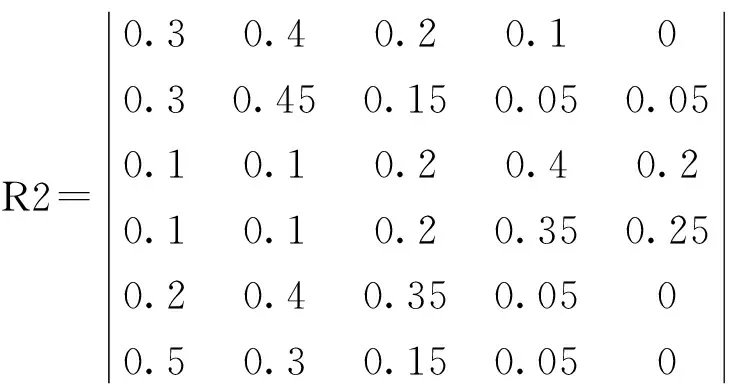
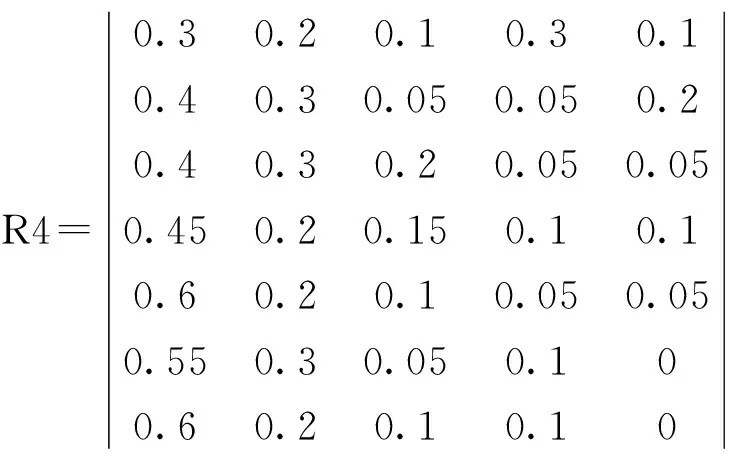
通過計算百分比得到模糊評價矩陣為

4.權重的確定

在一個多層次模糊綜合評判模型中，由于低一級層次的指標都是針對高一級子因素集所作的細化，因此，權重的分配是每一層次的各因素、各指標在所歸屬的相鄰上一層次的子因素集中所占的權數大小。權數大小根據重要性程度而定。通常可以用來計數的方法有兩兩比較法、德菲爾法(又稱為專家打分法)、調查統計法等。

用數學語言描述為，設權重集為W，則W={W1,W2,…,Wn}，其中Wi為二級指標因素的權重集，Wi={Wi1,Wi2,…,Wik}, (>0,j= 1,2,…,k),∑k=Wik=1。

權重的分配受到企業目標、文化以及董事會成員態度等因素的影響而有所不同。權重分配既要考慮各指標的相互關聯性，又要有所側重，所以根據評估團的經驗給各指標賦予一個權重，構成兩級權重向量。

(1)一級指標權重向量分別為U1=(X1，X2，X3，X4，X5)、U2=(X6，X7，X8，X9，X10，X11)、U3=(X12，X13，X14，X15)、U4=(X16，X17，X18，X19，X20，X21，X22)、U5=(X23，X24，X25，X26)、U6=(X27，X28，X29，X30，X31，X32，X33，X34)、U7=(X35，X36，X37)、U8=(X38，X39，X40，X41，X42)八組。權重向量：

W1=(0.4，0.2，0.2，0.1, 0.1)

W2=(0.2，0.3, 0.1, 0.2, 0.1, 0.1)

W3=(0.3，0.2, 0.2 ,0.3)

W4=(0.1,0.3, 0.2 0.1,0.1,0.15, 0.05)

W5=(0.3，0.2, 0.2 ,0.3)

W6=(0.2，0.2, 0.2 ,0.1, 0.1, 0.1, 0.05,0.05)

W3=(0.6，0.2, 0.2)

W3=(0.3，0.2, 0.2 ,0.15, 0.15)

說明在行業狀況因素中，項目組成員認為所處行業的市場與競爭對重大錯報風險的影響所占比重最大，為40%；生產經營的季節性和周期性與被審計單位產品相關的生產技術對重大錯報風險影響均為20%；能源供應與成本和行業關鍵指標統計數據對重大錯報風險影響各占10%。其它權重意義以此類推。

(2)二級權重向量分別為 U1、U2、U3、U4、U5、U6、U7、U8的權重向量：

W=(0.2,0.2,0.1,0.1,0.15,0.05,0.1,0.1)

5.合成運算

按照矩陣運算的法則權重向量與模糊矩陣的第一列兩兩配對，在與第一列配成的M對中每一對選擇兩個元素中較小的一個，構成一個有M個元素組成的向量，在整個向量中選擇最大那個元素作為模糊綜合評判向量中的第一個元素，也就是B中的b1，同理把權重向量與模糊關系矩陣中的其他列進行配對，運用最小最大法確定模糊綜合評判向量中的其他元素。

(1)進行一級綜合評價

設B1代表U1=(X1、X2、X3、 X4、X5)的綜合評判結果，B2～8代表U2～8的綜合評價結果。

B1=W1×R1=(0.4，0.2，0.2，0.1, 0.1)

運用MATLAB可求得B1=(0.3900 0.3150 0.1550 0.1050 0.0350)

同理可得，

B2= W2×R2=(0.2500 0.3150 0.1950 0.1550 0.0850)

B3=W3×R3=( 0.4250 0.1950 0.1350 0.1600 0.1050)

B4=W4×R4=(0.4475 0.2650 0.1025 0.0900 0.0950)

B5=W4×R4=(0.4150 0.3400 0.1550 0.0750 0.0150)

B6=W4×R4=(0.3875 0.3325 0.1500 0.0900 0.0400)

B7=W4×R4=(0.3600 0.2800 0.1700 0.1400 0.0500)

B8=W4×R4=( 0.4075 0.3025 0.1150 0.0950 0.0800)

上述結果B1～B8已是正規向量，所以無需進行模糊綜合評判向量歸一化。

結果說明，行業狀況對重大錯報風險影響的隸屬度為0.39，根據綜合模糊評判結果的最大隸屬原則進行評判，可得出依據行業狀況因素評估的重大錯報風險為低。同理，依據法律環境評估的重大錯報風險為較低。

(2)進行二級綜合評價

通過一級綜合評價，得出各因素風險水平有所差異，所以要想得出整個項目風險的準確評價，還要進行二級綜合評價。

由b1～b8可以得到二級綜合評價矩陣

R=(b1，b2，b3，b4， b5，b6，b7，b8)=

由二級權重向量，可得B=W×R=(0.2,0.2,0.1,0.1，0.15,0.05,0.1,0.1)×

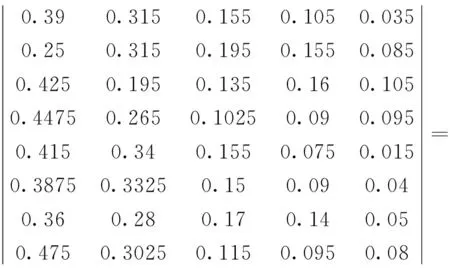
(0.3736 0.2979 0.1530 0.1162 0.0613)

同樣采用最大隸屬度法，得出被審計單位重大錯報風險評估為低水平，可以考慮接受該業務。

二、模型評價

該模型可以與數據庫技術相結合用于評估審計風險。隨著方法逐步完善，該方法的科學性、合理性、可行性和實用性有待在今后的實踐中不斷完善。運用該模型主要有以下優點：①避免憑經驗和主要決策者的個人偏好對目標項目進行選擇；②通過多目標的細分并對單個目標給予評價，有利于揭示被審計單位的真實情況，使設計的審計程序范圍、時間安排和內容更具科學性。

但是該模型在實際運用中還有待完善。①在運用模型時要考慮到特定項目中模型尚未考慮到的，但是可能會影響到重大錯報風險評估的因素變動；②運用該模型的過程中，相關數據的取得應該有更為嚴格的要求。比如權重向量的確定，以及模糊關系矩陣的投票人應該有較高的專業素養和職業道德，否則數據失真將直接影響到評判結果。被審計單位重大錯報風險評估的準確與否直接關系到事務所接受業務以后的審計程序，甚至會影響到審計報告的準確性。

總之，運用模糊綜合評價法可以綜合不同概率分布的專家意見，為定性指標較多的審計風險評價提供了一條有效的評價途徑。

三、討論

模糊綜合評價方法能較好的解決多目標決策問題，因此運用模糊綜合評價法分析被審計單位中諸因素對重大錯報風險的影響，并進行綜合評價是必要的。但由于所構建的評價指標體系各個指標之間并非完全獨立，調查問卷的樣本量還不夠大，用于檢驗的評價對象較少，以及方法的選擇不夠多樣化，使得最終評價的精確性可能會受到影響，未來研究可以在這幾個方面繼續深化。