細胞分析儀取液系統的改進型FORM算法可靠性評估
姜振海,黃煒祺,谷東偉,郭訓薇
(1.長春工業大學機電工程學院,吉林 長春 130012;2.南京華群光電技術有限公司,江蘇 南京 210000)
1 引言
加速壽命試驗是驗證復雜機械系統可靠性的重要方法,如何進行加速壽命試驗,如何在短期內獲得有效的試驗數據,如何有效的依據數據進行可靠性評估就顯得至關重要。
國內外關于加速壽命試驗的研究最早可以追溯到62 年前Levenbach 發表的論文《電容器的加速壽命試驗》[1];隨著加速壽命試驗理論的成熟,通過對現代航空發動機軸承進行全尺寸的加速壽命試驗[2],獲得導致軸承異常失效的原因,并通過對正在運轉的設備進行壽命評估的方式[3],提出在溫度循環環境下的試驗方法以及測試結果;在對潮汐渦輪葉片進行加速壽命試驗[4]中,提出在四種不同應力水平下,潮汐渦輪葉片在積累損害的同時,對設備的壽命進行研究;三腳架式CVJ加速壽命試驗[5]中發現粘著磨損現象,提出一種新的磨損壽命模型并結合運動學分析,驗證加速壽命試驗中所建運動模型的正確性;通過火炮的精度以及壽命研究,提供一種加速壽命試驗的研究理論[6?7],通過分析加載力、運行速度及額定動載荷,定義單因子及雙因子應力試驗的形式,明確加速因子、加速模型、誤差范圍以及加速壽命試驗步驟。
為進行可靠性評估,加速壽命試驗中常用到的方法有FORM(Fist?order reliability method)算法[8?13]、SORM(Second?order reli‐ability method)算法[14?15]、MC(Monte?Carlo)算法[16?18]。
FORM算法主要從模型的結構角度尋找極限狀態函數,根據變量確定函數曲線的維度,為尋找可靠性指標提供驗算點,但獲得的驗算點誤差較大,可靠度值存在較大爭議。
SORM算法主要從尋找極限狀態函數的曲線并進行二次求導,促使驗算點處的精度更高,誤差更小,但驗算點處的靈敏度過高。
MC 算法主要從大數據角度出發,針對模型的失效數據,通過偽隨機數的方式進行數據擴充并大量抽樣,為失效概率提供依據,盡管計算結果誤差小,但計算成本、所需樣本數高;此外,在MC算法的基礎上還運用MCMC技術[19]提高計算機模型的可靠性和準確性以及根據隨機變量在概率密度函數中可能遵循多模態分布這一特點,提出一種高精度概率不確定性傳播方法[20],當涉及多模態分布時,計算誤差較小,但計算難度大,不適用于實際工程中;以上幾種可靠性算法在進行可靠性評估時,會存在驗算點位置精度低、驗算點靈敏度高、計算成本高等問題,導致可靠性指標誤差變大、耗時長等狀況出現,從而降低設備可靠度。
由于改進型FORM算法能夠定位驗算點位置,降低驗算點的靈敏度,并且所需樣本數少,還能對加速壽命試驗所得出的失效數據進行優化分析,因此本文通過改進型FORM算法對細胞分析儀取液系統機械傳動結構的加速壽命試驗進行可靠性評估。
首先,通過分析設備的材料以及相關特性,確定加速模型和應力模型。
然后,利用加速壽命試驗與ADAMS 仿真技術相結合,針對易失效部件進行虛擬樣機技術仿真。
最后,改進FORM算法對加速壽命試驗得出的失效數據進行優化,減小誤差,提高可靠度。
2 加速壽命試驗與動力學仿真
由于取液系統機械傳動結構是細胞分析儀的重要組成部分,其可靠性直接影響細胞分析儀的使用效率,所以,針對加速壽命試驗以及動力學仿真,需要建立取液系統機械傳動結構三維模型并通過ADAMS(Automatic Dynamic Analysis of Mechanical Sys‐tems)進行模型處理以及應力分析,進而獲得應用于可靠性評估的失效數據。
2.1 加速壽命試驗與應力分析
為實現加速壽命試驗以及動力學仿真,首先通過CATIA 建立取液系統機械傳動結構模型,其機械結構模型,如圖1所示。
將模型導入ADAMS進行干涉檢查,通過布爾運算合并相同材質元件;并對運動部件進行運動副約束。
在ADAMS 中選取同步帶系統,并添加驅動及應力載荷,如圖2所示。
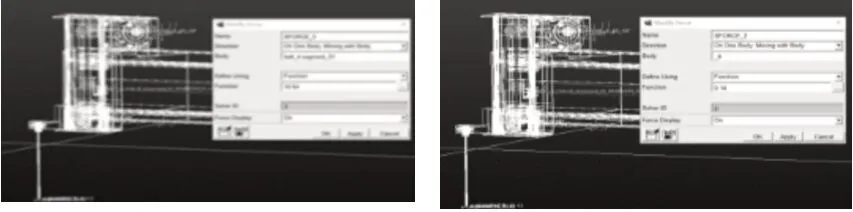
圖2 X、Y軸同步帶添加載荷Fig.2 Load Addition for Synchronous Belt of X and Y Axes
依據早期設備的故障數據進行分析,取液系統機械傳動結構的失效形式主要是同步帶斷裂,由于同步帶的故障基本屬于疲勞磨損,其疲勞壽命符合對數正態分布,因此選取公式(1)逆冪律模型進行加速壽命試驗分析。

式中:a,b—待估參數;φ(Pi)—應力函數;ui—疲勞壽命的對數均值。針對逆冪律加速模型,在標準環境下,室溫25℃,相對濕度55%RH,標準大氣壓101Pa。
加速因子的計算方法如式(2):
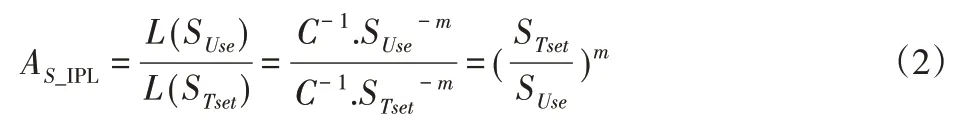
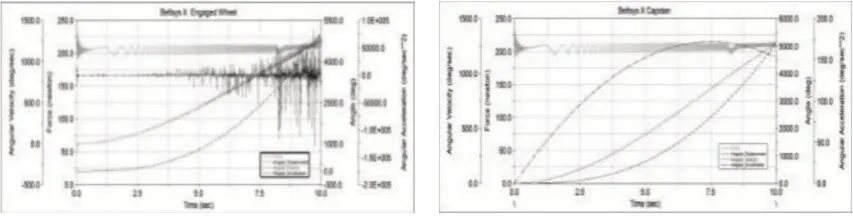
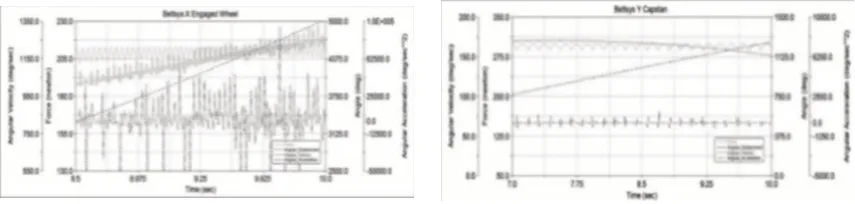
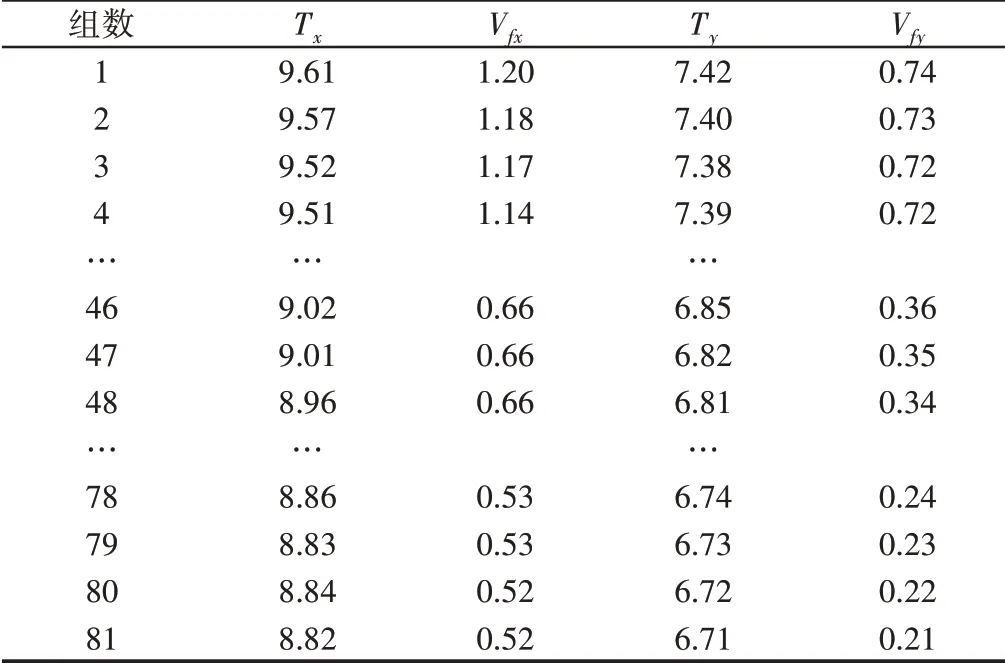
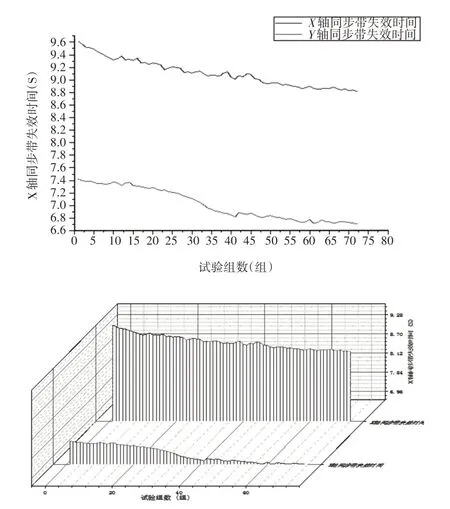
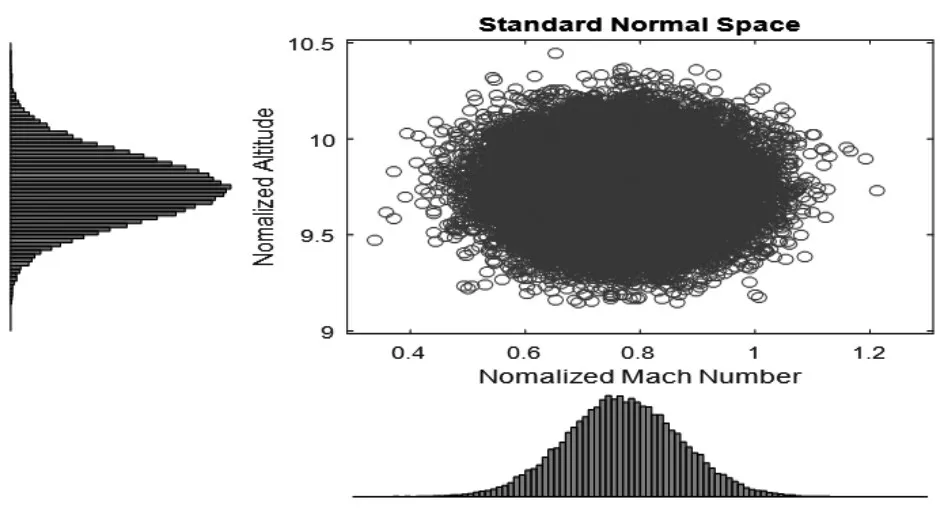
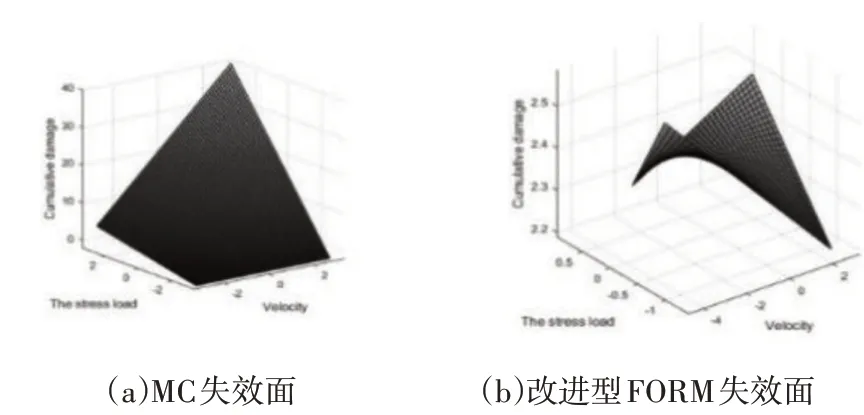
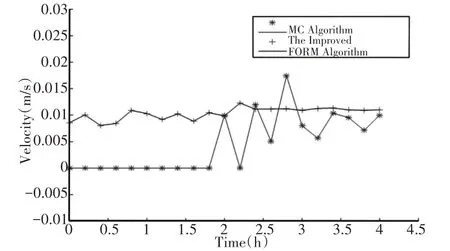
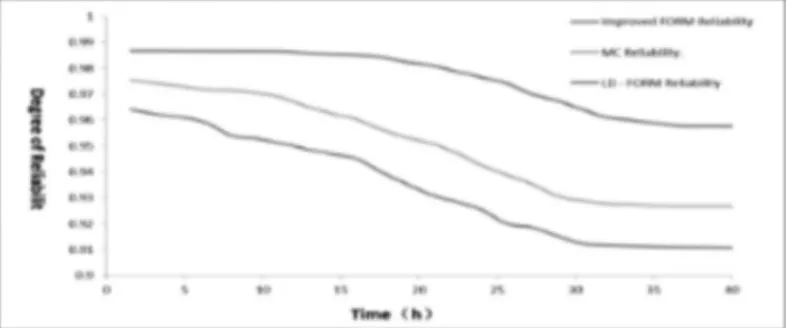
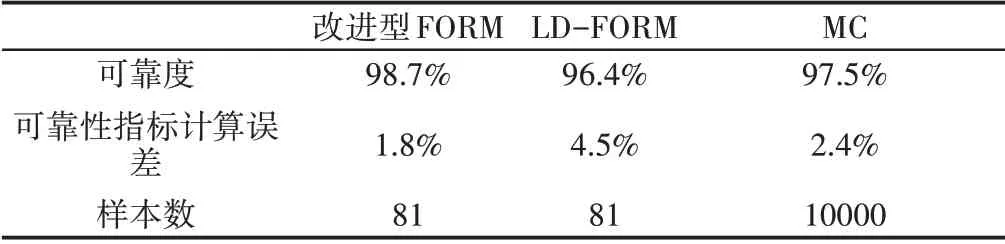
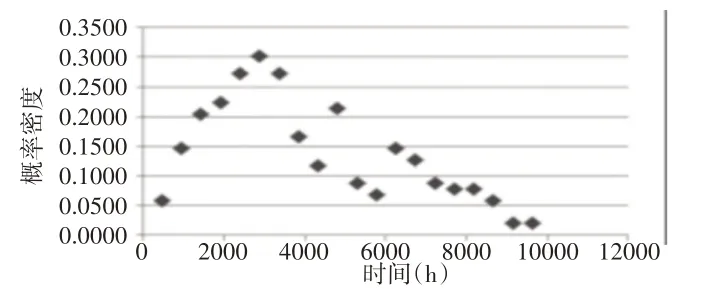
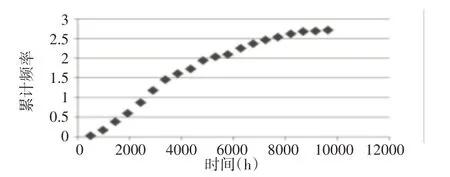
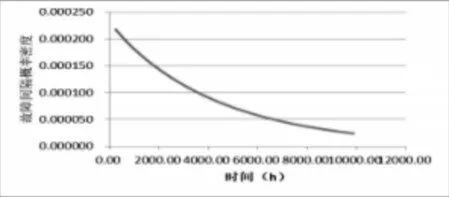
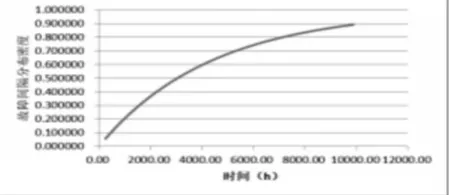
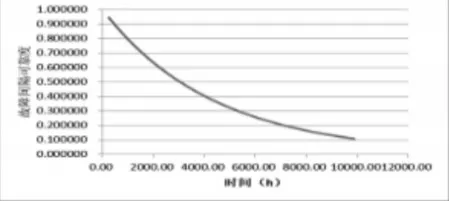
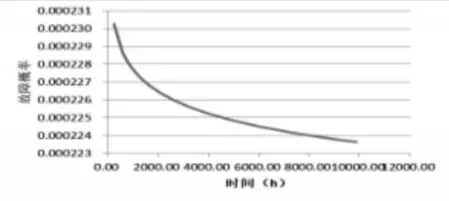
式中:m—加速率常數,2 其中關于m的取值,一般電容器以直流電壓V加速,m=5;滾珠軸承及鋼材的斷裂,m=3?4。由于血細胞分析儀取液系統的材料為鋁合金,其中同步帶為聚氨酯材質,因此選擇的加速率常數m=4。 測試使用應力STset根據同步帶材料以及相關特性,同步帶所能承受的最大應力,明確應力范圍: 式中:V—同步帶所受載荷時的速度;F—對同步帶施加的應力;V0—同步帶的初始速度;M—同步帶自身重量以及所承受的重量;P—同步帶承受的載荷;S—同步帶的受力面積;Mbelt—同步帶自身的重量;Mbearing—同步帶所承受的重量。 式中:N—正壓力;μ—摩擦系數,同步帶材質為聚氨酯,因此摩擦系數0.5;f—摩擦力。 通過式(3)獲得同步帶所受載荷與速度的應力范圍。通過計算得知X軸同步帶工作時所允許的最大速度為0.06m/s,Y軸同步帶工作時所允許的最大速度為0.11m/s,X軸同步帶工作時所允許的最大正應力27.28N,由于是滑動摩擦,因此根據式(4)可知同步帶帶動同步輪的摩擦力為13.64N,Y軸同步帶工作時所允許的最大正應力0.32N,即同步帶帶動同步輪的摩擦力為0.16N。根據血細胞分析儀取液系統的工作機制,X軸同步帶運轉速度最小0.05m/s,Y軸同步帶運轉速度最小0.09m/s,X軸同步帶最小正應力21.28N,即同步帶帶動同步輪的摩擦力為10.64N,Y軸同步帶最小正應力0.28N,即同步帶帶動同步輪的摩擦力為0.14N,因此,X軸同步帶速度的加速因子AS1=2.07;Y軸同步帶速度的加速因子AS2=2.21;X軸同步帶摩擦力的加速因子AS3=2.61;Y軸同步帶摩擦力的加速因子AS4=1.69。 綜合加速因子計算根據式(5)得出: 式中:AS1—X軸同步帶速度的加速因子;AS2—Y軸同步帶速度的加速因子;AS3—X軸同步帶摩擦力的加速因子;AS4—Y軸同步帶摩擦力的加速因子。 所以,綜合加速因子As?all=20.17。因此通過允許的最大應力,并在[Vmin,Vmax]與[Fmin,Fmax]中進行速度與所受載荷的正交試驗,同時根據機械設計手冊對同步帶與同步輪的安裝要求、轉速要求、材料要求以及摩擦力極限要求,正交試驗中在[Vmin,Vmax]與[Fmin,Fmax]中的數據變化精度要符合規定范圍,速度在(0.005~0.01)m/s的范圍內,摩擦力在(0.5~1)N之間變化。 81組正交試驗數據,如表1所示。 表1 同步帶的速度與所受載荷Tab.1 Speed and Load of Synchronous Belt 為驗證同步帶失效與速度和所受載荷之間的關系,選取第81組數據,當所有應力都處在最大時進行分析,通過圖3和圖4可知,X、Y軸同步帶在啟動時,參數瞬間發生躍升,Y軸同步帶僅在啟動瞬間,參數急劇爬升,之后趨于穩定并逐漸降低。 圖3 X軸同步帶主從動輪Fig.3 X?Axis Synchronous Belt Master and Slave Drive X軸同步帶在啟動后,速度、力、位移以及加速度在呈現短時間波動后,速度和位置持續爬升,加速度產生劇烈波動,受力情況持續上升,X軸的同步帶失效的范圍在(210~230)N,Y軸的同步帶失效的范圍在(280~300)N。 因此,通過圖4和圖5可以看出,全部參數達到加速極限后,當8.82s時,X軸加速度降低幅度過大,因此X軸發生失效的時間為8.82s時,此時應力為229.1N;當6.71s時,Y軸速度與加速度均降速幅度過大,因此Y軸發生失效的時間為6.71s 時,此時應力為295.8N,X軸失效速度為0.52m/s,Y軸失效速度為0.21m/s。 圖4 Y軸同步帶系統主從動輪Fig.4 Y?Axis Synchronous Belt System Master and Slave Drive 圖5 X、Y軸同步帶參數局部圖Fig.5 Local Diagram of X and Y Axis Synchronous Belt Parameters 通過細胞分析儀取液系統的失效機理判定,不論X軸或者Y軸的同步帶發生失效,都判定取液系統整體發生失效故障,X、Y軸同步帶失效時間,如表2所示。 表2 X、Y軸同步帶失效時間Tab.2 Failure Time of X and Y Axis Synchronous Belt 由于細胞分析儀取液系統是傳輸系統,因此,無論X軸還是Y軸的同步帶,只要有一根損壞,整個系統都無法進行工作,因此從圖6中可以看出,同組試驗的前提下,Y軸的同步帶失效時間比X軸同步帶失效時間短,從整體數據來看,Y軸時間一直小于X軸時間,因此,將Y軸同步帶的失效時間作為細胞分析儀取液系統的失效時間。 圖6 X、Y軸失效時間Fig.6 Failure Time of X and Y Axes 通過表2獲得取液系統機械傳動結構中同步帶的所受載荷和速度的極限狀態函數: 式中:Tn—任何應力時的失效時間; α1—X軸速度的加速因子AS1=2.07; α2—Y軸速度的加速因子AS2=2.21; α3—X軸承受應力的加速因子AS3=2.61; α4—Y軸承受應力的加速因子AS4=1.69; ?x—X軸失效節點處的應力值; ?y—Y軸失效節點處的應力值。 對式(6)進行泰勒展開并通過最小二乘法獲得矩陣常數項,最終得到極限狀態函數(7): 改進型FORM算法在LD?FORM算法的基礎上通過MC算法進行可靠度精度修正。利用LD?FORM 算法對失效數據的分析得到極限狀態函數以及驗算點,再通過Nataf變換原極限狀態函數曲線以及Schmidt構造的正交陣進行旋轉坐標軸,新的坐標軸指向驗算點方向的方式,將原可靠度列式進行轉換,通過MC算法以及牛頓迭代法求解非線性方程組的方式來計算失效概率,最終獲得精度較高的可靠度。 為提高可靠度精度,將加速壽命試驗得出的極限狀態函數曲線通過Nataf分布方法對X空間進行變換到u空間,在u變量空間的極限狀態函數曲線(x)=G[T?1(u)]=g(u)。 計算極限狀態函數曲面g(u)=0上的最有可能失效點u(?驗算點)。由于抽樣尋找驗算點的方式過于抽象,如圖7所示。 圖7 抽樣尋找驗算點Fig.7 Sampling to Find Check Points 因此,通過響應面的方法,由失效面尋找最有可能失效點會更加直觀。通過對比圖8(a)的MC算法的失效面以及圖8(b)改進型FORM算法的失效面,發現改進型FORM算法的失效面曲率大,MC算法的失效面曲率小。 通過圖9的對比分析,最有可能失效點的收斂速度與失效曲面的曲率之間是相關的,如圖8(a)可知失效面的曲率小,驗算點定位有極大的誤差,無法找到圖9最后趨近的精準驗算點,與之相反,如圖8(b)所示,當曲率變大時,越容易尋到精確的驗算點。因此改進型FORM算法通過響應面法來尋找驗算點是可行的,通過減小尋找驗算點的誤差,進而求出的β值的精度更高。 圖8 MC、改進型FORM算法失效面Fig.8 Failure Surface of MC and Improved FORM Algorithm 圖9 改進FORM算法與MC算法趨近準確驗算點的收斂速度Fig.9 Convergence Rate of the Improved FORM Algorithm and MC Algorithm Towards Accurate Verification Points 為了進一步提高驗算點精度,將獨立標準正態隨機變量u的坐標系進行坐標變換,設新坐標系為u′,新坐標系的坐標軸為u′n指向驗算點u?方向。 滿足這樣條件的坐標變換矩陣為正交陣H,H的第n列為驗算點方向的單位向量,如式(8)所示。 式中:||·||—向量求模。 H陣的構造可用Schmidt正交化方法實現,u’坐標系和u坐標系隨機變量的相互關系為:u=Hu′,u′=HTu。相應的u′坐標系下極限狀態函數g(u)變為:g(u)=g(Hu′) =g′(u′)。 在u′坐標系下極限狀態函數g′(u′) =0曲面在新的平面上。將原可靠度列式變換成如下表達式: 式中:[·]—0~1函數,當自變量小于零時取1,自變量大于零時取0;?n(·)—獨立標準正態隨機變量向量的聯合概率密度函數為向量-u′的函數,使得 下列公式(10)視為一個條件失效概率計算表達式: 式(10)可采用Monte?Carlo法來求解,首先生產(n?1)維獨立標準正態隨機變量樣本,設樣本數目為N,則 式(11)中的統計量通過下列非線性方程來求解: 基于上述的加速壽命試驗以及虛擬樣機仿真技術,分別用改進型FORM算法、LD?FORM算法以及MC算法對81組失效數據進行算法優化。 三種算法對細胞分析儀取液系統機械傳動結構隨時間的變化所獲得可靠度,如圖10所示。 圖10 三種算法可靠度對比Fig.10 Reliability Comparison of the Three Algorithms 如圖所示,三種算法優化的數據結果都呈現出遞減的現象,但LD?FORM算法處理的數據曲線波動較大,可靠度值從96.4%下降到91.0%,總體來看設備可靠度下降5.4%。 MC算法處理的數據曲線較LD?FORM 算法來看,波動變化較小,總體可靠度值整體有所提高,從97.5%下降到92.6%,下降范圍4.9%。 改進型FORM算法較LD?FORM算法以及MC算法來看,可靠度值總體下降平滑,無較大波動,同時可靠度初始值高于其他兩種算法,下降范圍僅為2.9%,明顯小于其他兩種算法。 因此,基于上述分析,改進型FORM算法在優化數據方面明顯優于其他兩種算法,為可靠性評估提供了有效的設備基礎數據。 通過文獻[11]可知可靠性指標的計算誤差以及計算改進型FORM算法中隨機變量的靈敏度指標,判斷影響因子,細胞分析儀取液系統機械傳動結構隨機變量靈敏度指標的重要度,如圖11所示。X1=15%,X2=25%,X3=60%。 圖11 隨機變量靈敏度指標Fig.11 Sensitivity Index of Random Variable 通過表3以及圖11分析可知,由相同樣本數對加速壽命試驗數據進行處理時,改進型FORM算法可靠度比LD?FORM算法精度高,可靠性指標計算誤差小。 表3 三種算法評估分析Tab.3 Evaluation and Analysis of Three Algorithms 在樣本數量遠小于MC算法時,可靠度以及可靠度指標高于MC算法。通過文獻[11]中靈敏度指標的計算,在加速壽命試驗數據為基礎的改進型FORM算法進行優化后,可以分析極限狀態函數中隨機變量的重要度,進而判斷失效因子中哪個因子是最重要的。 通過計算結果可知,同步帶所受載荷X3是最重要的失效因子。 因此,改進型FORM算法在可靠性評估上,減小可靠性指標計算誤差,提高可靠度并提供失效因子重要度分析,使可靠性評估在有效節約時間以及經濟成本的同時,其結果更加真實可信。 通過對全國醫院的細胞分析儀取液系統的322組維修記錄數據來看,根據觀測值求取概率密度函數、分布函數、可靠度函數和故障率函數,通過計算獲得平均無故障時間(MTBF),從而有效獲得細胞分析儀取液系統試驗臺的可靠度值并與改進型FORM算法進行對比。 根據組距將322組數據分為20組,并對20組數據進行計算獲得故障間隔時間的概率密度和故障間隔時間的經驗分布函數三點圖,如圖12、圖13所示。 圖12 故障時間概率密度Fig.12 Failure Time Probability Density 通過圖12和圖13可以看出該血液細胞分析儀故障間隔時間可能服從威布爾分布或指數分布。 圖13 故障時間經驗分布Fig.13 Failure Time Experience Distribution 因此利用一元線性回歸分析和最小二乘法,依據故障數據進行參數估計,并運用相關系數法來檢驗威布爾分布,可以確定該血液細胞分析儀故障間隔時間的分布規律。 根據計算獲得線性回歸方程: 對于威布爾分布的擬合效果,利用相關系數法對其進行檢驗,顯著性水平α=0.10,經檢驗,細胞分析儀故障間隔時間服從威布爾分布。 進一步對細胞分析儀故障間隔時間分布函數進行D檢驗,顯著性水平α=0.10,經檢驗,細胞分析儀故障間隔時間服從威布爾分布。 通過式(14)獲得故障間隔時間的概率密度函數、式(15)獲得分布函數、式(16)獲得可靠度函數以及式(17)獲得故障率函數。 該血液細胞分析儀故障間隔時間的概率密度函數、分布函數、可靠度函數和故障率函數分別,如圖14~圖17所示。 圖14 概率密度函數 Fig.14 Probability Density Function 圖15 分布函數Fig.15 Distribution Function 圖16 可靠度函數 Fig.16 Reliability Function 圖17 故障率函數Fig.17 Failure Rate Function 綜合上述分析,全國醫院的細胞分析儀取液系統的322組維修記錄數據服從威布爾分布的同時,通過對概率密度函數、分布函數、可靠度函數和故障率函數的計算,經由MTBF計算獲得細胞分析儀取液系統的可靠度值,計算公式,如式(18)所示。 式中:f(t)—故障間隔時間的概率密度函數。 針對全國醫院的細胞分析儀取液系統的MTBF計算結果,如式(19)所示。 因此可靠度值為99.2%。 這里通過ADAMS 虛擬樣機技術對細胞分析儀取液系統機械傳動結構的速度與所受載荷的正交試驗數據進行加速壽命試驗仿真,獲得細胞分析儀取液系統機械傳動結構失效數據。 通過改進型FORM算法獲得可靠度為98.7%,與維修數據計算MTBF獲得的可靠度99.2%相比,改進型FORM算法在可靠性指標計算誤差方面,誤差小于LD?FORM算法和MC算法,所需樣本數少,精度更高,更加貼近實際數據。 與此同時,改進型FORM算法可以針對靈敏度指標,通過獲取的機械設備失效因子重要度,使可靠性評估更加完善。



2.2 仿真分析


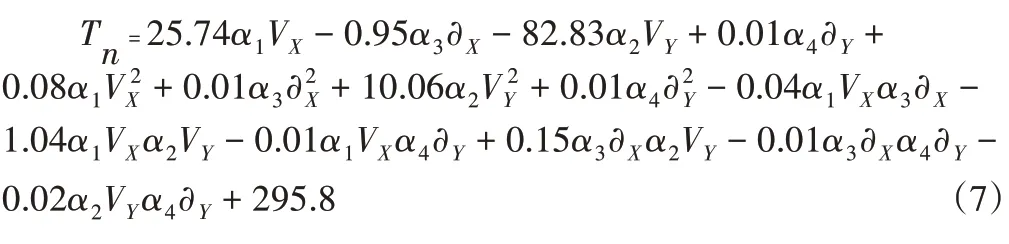
3 改進型FORM算法評估
3.1 算法原理

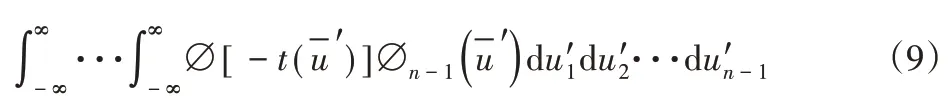



3.2 算例分析

4 數據驗證對比
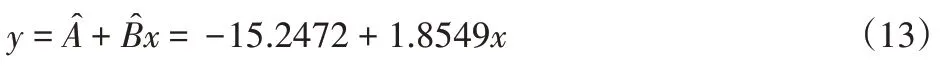

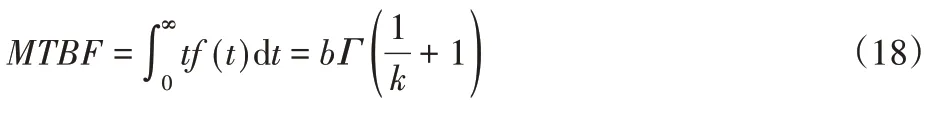
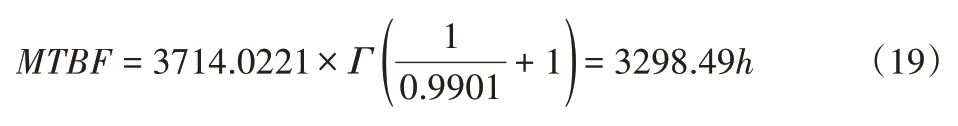
5 結論

