基于多智能體強化學習的軌道追逃博弈方法

許旭升，黨朝輝，宋 斌，袁秋帆，肖余之

（1.上海宇航系統工程研究所，上海 201109；2.西北工業大學 航天學院，陜西 西安 710109）

0 引言

近年來，隨著空間領域科學技術的迅猛發展，越來越多的國家開始發射自己的衛星。雖然宇航科學造福的范圍越來越大，但是太空中存在的太空垃圾和失效航天器也越來越多。這些失效航天器大多以第一宇宙速度繼續在軌。若在軌航天器與這些失效航天器的軌道相交或者重合時，來不及躲避將會產生猛烈的撞擊，嚴重威脅到一些高價值衛星和重要空間資源。于是，針對失效航天器的“在軌服務”也開始逐漸在一些航天國家得到重視。美國等國家已經開展了針對非合作目標的在軌服務的研究，并進行了一系列實驗。

在非合作目標的在軌服務研究中，有一類較為重要的問題就是具有機動能力的非合作目標的交會問題。由于非合作目標的機動能力未知，而太空中航天器燃料有限，所以將此類問題可以轉換為航天器的追逃博弈問題，逃逸者即為失效航天器，追捕者則為在軌服務衛星。在這類問題中考慮到多個衛星協同工作，共同實施對非合作目標的捕獲，因此成為多對一軌道追逃博弈問題。

針對衛星追逃博弈問題，國內外學者已經進行了深入而廣泛的研究。目前主要以微分對策求解的方法為主。文獻［6］通過將追逃博弈問題轉換為高維時變非線性兩點邊值問題，再進行數值求解的方式得到追逃策略。文獻［7］利用半直接配點法對微分對策博弈過程進行求解，得到相應的數值解。文獻［8］利用最優控制方法，通過求解微分對策的鞍點得到追逃博弈策略。集群追逃博弈問題中，僅知自身狀態和非合作目標有限狀態，未知非合作目標的未來機動信息和行為策略，且在集群衛星之間也難以形成完全狀態的交流，利用微分博弈的數值方法求解比較復雜。

近年來，隨著深度強化學習的興起，有些學者找到了另外一種解決博弈問題的途徑，即利用深度學習的方法對環境進行建模，然后不斷訓練策略，直至獎勵值達到最優，完成最優博弈策略的求解。以深度強化學習為主的智能算法開始逐漸應用于求解這類復雜問題的過程中，文獻［10］通過構建模糊推理模型，將多組并行神經網絡的分支深度強化學習架構引入到非合作目標追逃博弈策略求解的過程中。文獻［11］利用深度Q網絡（Deep Q-Networks，DQN）和最大最小（MiniMax）算法求取了近距空戰中的最優機動策略。文獻［12］將平均場理論與多智能體強化學習算法（Multi-Agent Reinforcement Learning，MARL）相結合，對無人機集群進行了細粒度任務規劃。符小衛等利用改進的分布式多智能體深度確定性策略梯度算法（Multi-intelligent Deep Deterministic Policy Gradient，MADDPG），驗證了在多無人機協同對抗快速目標的追逃博弈問題中的協同圍捕效果。深度學習由于其強大的擬合能力，被廣泛應用于各類追逃博弈問題中。本文將利用MADDPG 算法，對追逃博弈問題展開研究。

1 問題描述與建模

1.1 多對一衛星追逃博弈問題

假設有這樣一類場景，集群衛星編隊在正常運行，在相對軌道上有一個非合作目標，該目標對編隊衛星構成了嚴重的威脅，需要集群衛星協同與該非合作目標進行博弈，最終將其抓捕。而這個過程中就涉及一類博弈問題，即集群衛星追逃博弈問題。傳統的方法通常是考慮博弈過程中的時間或燃料消耗，將其轉換為非合作目標的最優交會問題，或者是利用微分博弈的方法，在假設對方策略是理性的前提下進行自身最優博弈策略的求解。

本文研究的多對一衛星追逃博弈是個動態的過程，博弈參與者被定義為追捕衛星和逃逸衛星，博弈雙方具有相反的博弈目標，即追捕衛星需要盡力追擊和捕獲逃逸衛星，而逃逸衛星則需要盡可能地避開和遠離追捕衛星。而在這個過程中，涉及衛星的許多真實約束，比如追捕衛星之間需要協同好策略，避免相撞，優化相互之間的策略，使得燃料消耗等指標實現最優。多對一衛星博弈場景如圖1所示。

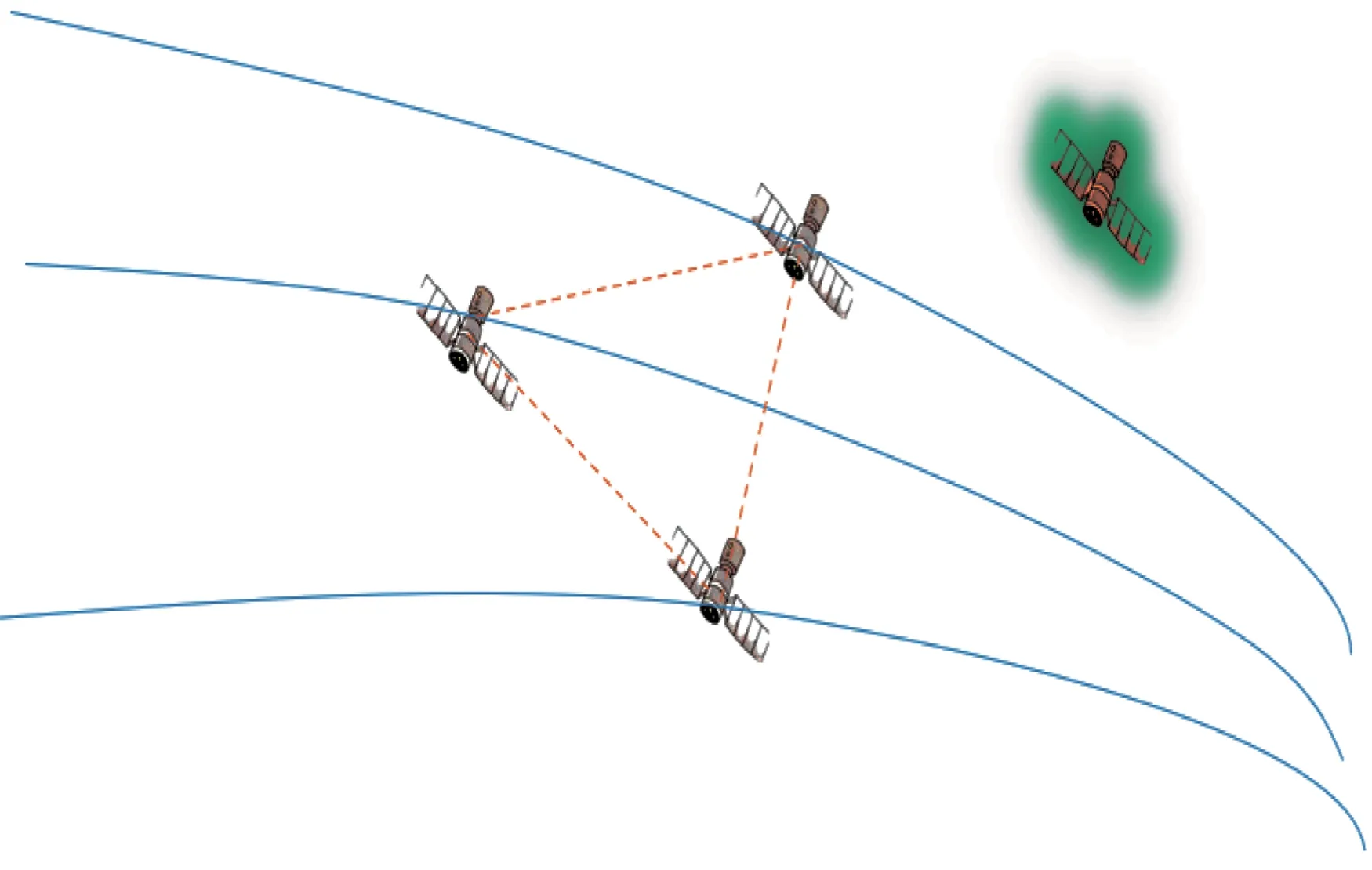
圖1 多對一衛星追逃博弈場景Fig.1 Many-to-one satellite pursuit-evasion game scenario

圖1 中，P(=1，2，…，)為追捕衛星。為方便距離和速度的確定，假設有一個虛擬衛星，此衛星的軌道根數為在博弈開始前的追捕衛星的平均軌道根數。在此衛星的相對軌道坐標系下，追捕衛星和逃逸衛星之間進行博弈，轉換為數學模型如圖2 所示。

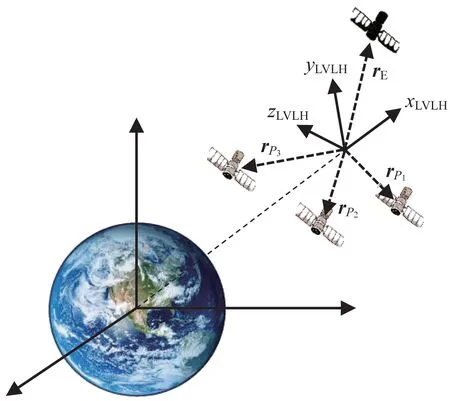
圖2 博弈場景軌道坐標系Fig.2 Orbital coordinate system of the pursuit-evasion game scenario

在圖2的軌道坐標系下，為逃逸衛星的位置，r，r，…，r為個追捕衛星的位 置，為逃 逸衛星的速度，v，v，…，v為個追捕衛星的速度。本文針對以上多星追逃博弈問題，構造出了集群衛星追逃博弈數學模型。

在本文研究的追逃博弈問題中，追捕衛星需優化策略去追擊和捕獲逃逸衛星，而逃逸衛星則也需要不斷優化策略去避開和遠離追捕衛星，雙方的博弈構成了零和微分博弈問題。但是，在追捕衛星之間需要協調和配合完成一定的博弈目的，每個追捕衛星又相當于一個合作博弈問題，通過對博弈模型建模，利用數學模型對雙方的博弈策略進行表示。雙方的博弈策略數學模型如下：

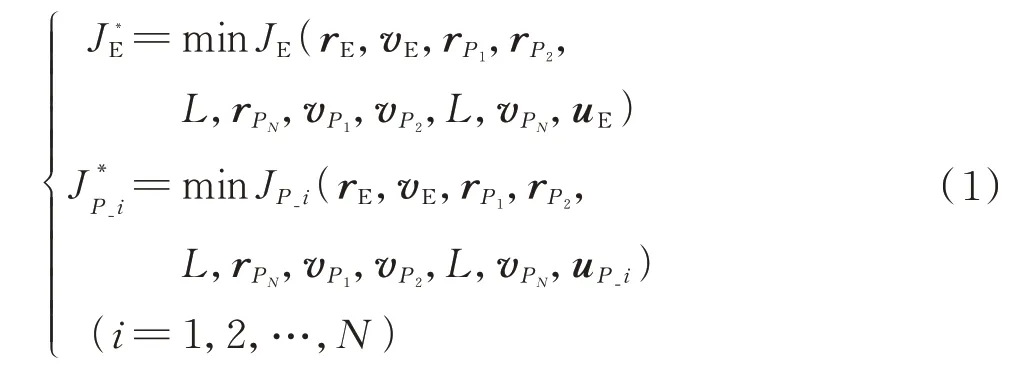
式中：、J為參與博弈的衛星的機動策略代價函數。

參與博弈的逃逸衛星和每一個追捕衛星都根據代價函數優化自己的策略，目的是使得自己對應的代價函數最小。由于每一個博弈參與者的博弈策略都會影響到最后的博弈結果，而在博弈過程中博弈雙方必然需要優化自己的策略到達最優。因此在進行博弈時，假設雙方為理性，最終策略將形成納什均衡條件，即：若在博弈過程中有一方策略不是最優，則另一方博弈成功的概率將會增大。這個過程數學描述為

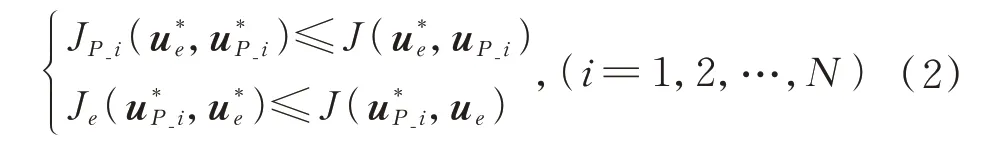
在式（2）中，當一方的衛星采用了納什均衡策略下的動作，而對方為非理性策略，即采用納什均衡策略以外的動作，都將使得對方的目標函數無法取得最優。

因此，在衛星追逃博弈模型中，通過求解以上最優化問題得到納什均衡策略，從而實現追逃博弈的最優機動。

1.2 衛星動力學建模

在空間多衛星追逃博弈過程中，忽略攝動因素，衛星滿足基本的二體軌道動力學。在軌道坐標系下，假設博弈開始前追捕衛星圍繞著一顆虛擬參考星運行，而與非合作目標的相對距離遠遠小于參考星軌道運行半徑，由于衛星在相對軌道坐標系下運動，所以其動力學模型忽略3階以上小量，可描述為

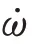
衛星的機動加速度約束公式如下：

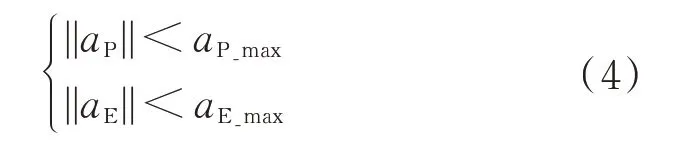
式中：、為追捕衛星和逃逸衛星的機動加速度；、為機動能力約束。

通常情況下，根據博弈的平衡性考慮，當參加博弈的雙方數量有差異時，需要在機動能力上平衡，即當＞時，＜。

由于本文假定整個追逃博弈過程均在可觀測的參考系軌道下，因此，規定追捕衛星和逃逸衛星的博弈機動范圍為

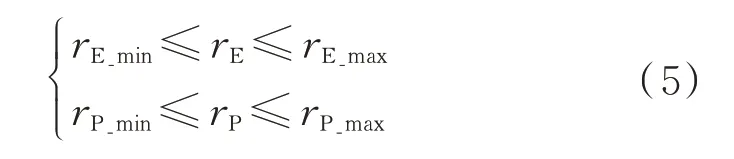
同時，對博弈結果也進行相應的定義，由于在追逃博弈問題中，雙方的博弈目的是追捕和逃逸，考慮到衛星間交會時速度與位置必須同時一致，否則將會進行碰撞產生損壞，因此，定義博弈中追捕成功的條件為

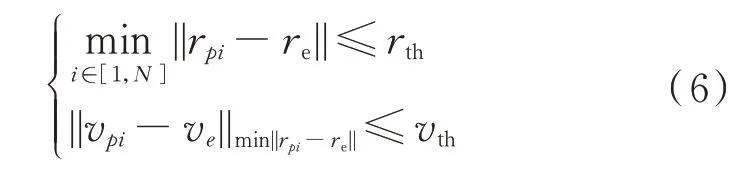
式中：第1 部分為追捕衛星中的某一顆衛星與逃逸衛星之間的距離小于等于一定的距離閾值；第2部分為當其中一顆衛星與逃逸衛星距離最近時，相對速度也小于等于一定的速度閾值。當兩部分同時滿足時，則定義為追捕博弈行為成功；否則，則為逃逸博弈行為成功。

2 MADDPG 算法

2.1 強化學習算法

在本文的多對一衛星追逃博弈模型中，將每個衛星看作為一個智能體，利用強化學習的方法優化策略，最終追捕衛星和逃逸衛星各自得到其最優策略，達到納什均衡狀態。

在強化學習模型中，智能體通常通過“感知信息—執行動作—獲得獎勵”的方式與環境進行交互，在這個不斷迭代的過程中進行策略的優化學習和訓練。首先，智能體通過接受環境的信號輸入即環境狀態；之后根據狀態利用自身的策略轉化輸出動作a，該動作與環境交互，產生獎勵r，智能體接受該獎勵并根據獎勵的值進行調整自身的策略，以獲得的獎勵值最大為目標，不斷進行迭代；最終優化得到自身對于環境最優的策略。

MARL 是一類基于馬爾可夫決策過程的隨機博弈算法，本質過程與單智能體強化學習算法一樣，都是通過不斷地感知信息、輸出動作，獲得獎勵反饋，不斷迭代優化的過程，但是MARL 中由于多個智能體共同作用于環境，因此利用馬爾可夫博弈描述如下：

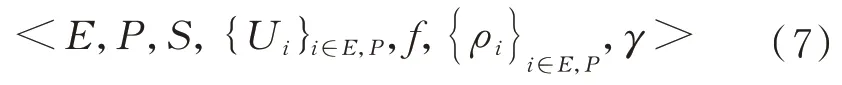
式中：為追捕智能體；為逃逸智能體；為模型的環境狀態空間；{U}為智能體的動作空間；：××→[0，1]為狀態轉移概率分布；{ρ}：××→R，∈為獎勵函數；為獎勵衰減系數。

多智能體算法可以由不同任務進行設計，比如完全合作、不完全合作、合作對抗等。本文模型中假設追捕衛星和逃逸衛星均為智能體，雙方都參與策略的優化，追捕衛星之間為完全合作，與逃逸衛星之間為對抗關系。

2.2 MADDPG 算法原理

由于在多智能強化學習算法中，每個智能體在訓練學習策略的時候，其他智能體的動作未知，將導致環境非平穩，因此，當智能體數量變多時策略往往難以收斂。MADDPG 是一種在多智能體強化學習領域十分受歡迎的算法，各個智能體采用DDPG 的結構，同時利用一個全局的“演員-評論家”（Actor-Critic）架構，使得各個智能體利用“集中訓練，分散執行”的方法，尋找到最優的聯合策略。通過這種方式，充分考慮到每個智能體的策略，集中訓練時作為整體進行優化，在執行的時候各個智能體僅僅利用觀測到的信息進行預測，解決了環境不平穩的問題。

MADDPG 算法的核心是“集中訓練”的“演員-評論家”結構，考慮有個智能體，每個智能體對應有自己的決策網絡，這個決策網絡的輸出就是對應智能體的策略輸出。在進行集中訓練時，各個智能體利用觀測信息通過決策網絡后進行策略輸出對應的動作(π)，同時每個智能體利用一個能夠接收全局信息的評價網絡，對智能體決策網絡的輸出進行評估，得到每一個智能體輸出動作對應的值函數Q。智能體的決策網絡接收該評價信號，進行自身策略π的調整和優化。通過這種方式，每一個智能體的Actor 網絡雖然接收局部觀測信息輸出動作，但是在全局的評價網絡評價校正下，每一個智能體的策略都是將其他智能體考慮在內的全局最優策略。因此，在訓練完畢最后執行的時候，智能體僅僅通過局部觀測信息，而不需要其他智能體的策略就能夠輸出考慮到全局的策略動作，以此達到了分散執行時整體最優的效果。MADDPG 算法原理如圖3 所示。

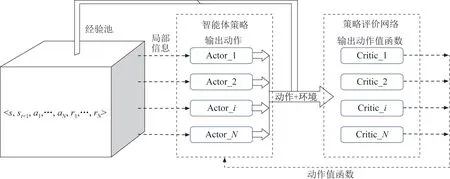
圖3 MADDPG 算法原理圖Fig.3 Schematic diagram of the MADDPG algorithm

MADDPG作為一種“演員-評論家”（Actor-Critic）結構的MARL，在訓練優化參數時，主要有2 部分組成，一部分是全局Critic 網絡的更新，另一部分是各個智能體決策網絡參數的優化更新。MADDPG 在訓練的時候，每一條經驗池中的樣本數據包括＜，s，，…，a，，…，r＞，即當前全局狀態、動作后全局的狀態、各智能體的動作與相應的獎勵。

評價網絡輸入為全局信息的觀測，輸出為各智能體輸出動作的評估，值的計算可以表示為=(s，，…，a，θ)，利用獎勵值對評價網絡進行更新如下：

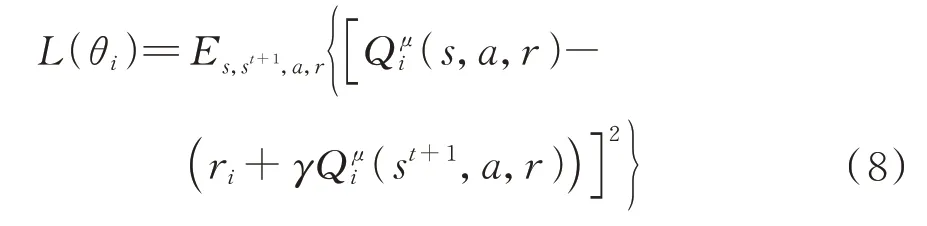
動作值函數利用當前時刻估值和動作后獎勵校正后估值的均方差的方式進行更新，相當于全局的中心評價網絡，有效地解決了環境不平穩的問題。

每個智能體擁有一個接收環境中狀態信息輸出動作的策略網絡，在進行訓練時，根據評價網絡輸出的動作值函數得到累積期望收益的梯度進行策略參數的更新。考慮到整體博弈策略是由個智能體的參數={，，…，θ}形成的策略={，，…，π}組成的，在進行集中訓練時，根據貝爾曼方程在隨機策略下，每個智能體的累積期望收益(θ)及其梯度? J(θ)為

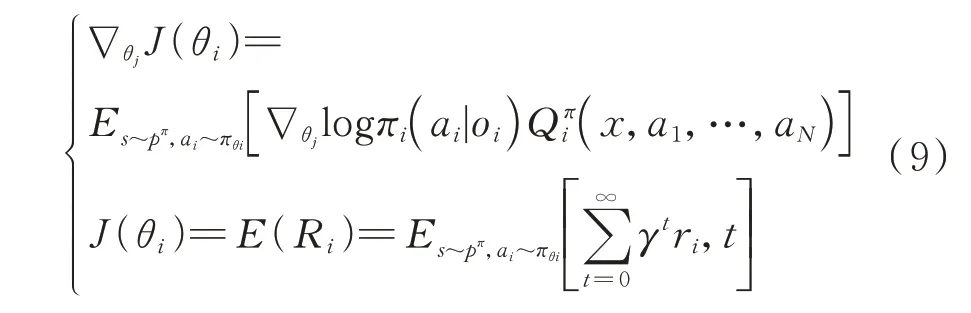
由于采用MADDPG 的確定性策略梯度，因此其更新的策略梯度如下：

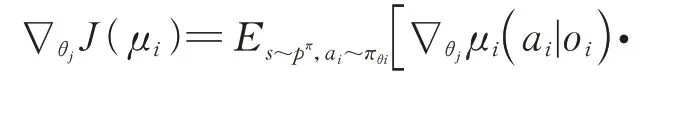
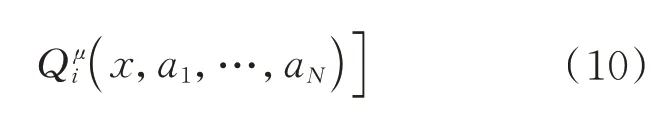
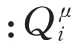
通過上述更新過程，在訓練過程中決策網絡和評價網絡同時更新，抽取經驗池中的數據。當然在算法設計過程中，雙網絡參數差分更新等方法不再贅述，最終完成網絡的更新。

3 基于MADDPG的空間軌道追逃博弈實現

在軌道追逃博弈過程中，為使得博弈策略完整真實，追捕衛星和逃逸衛星均可看作為智能體，共同在環境中進行追逃博弈訓練，最終優化得到的策略將能夠充分考慮到對方的策略和機動輸出，實現最優的博弈目的。本文基于多智能體深度確定性策略梯度的方法，利用決策-評價網絡結構得到最優多個追捕衛星的協同策略，同時，逃逸衛星也在訓練中博弈迭代，實現最優逃逸策略的求解。而每一個智能體按照相應的指標將優化得到其最優的策略，相互之間達到了納什均衡。

最后在實施抓捕目標衛星時，只要目標衛星的機動方法不是最優的策略，將得到更好的博弈效果。

追逃博弈算法整體方案如圖4 所示。為達到博弈目的，訓練前需要對每個智能體進行獎勵塑造（Reward Shaping）。根據博弈目的和方法的區別，分為追捕衛星博弈獎勵函數和逃逸衛星博弈獎勵函數。

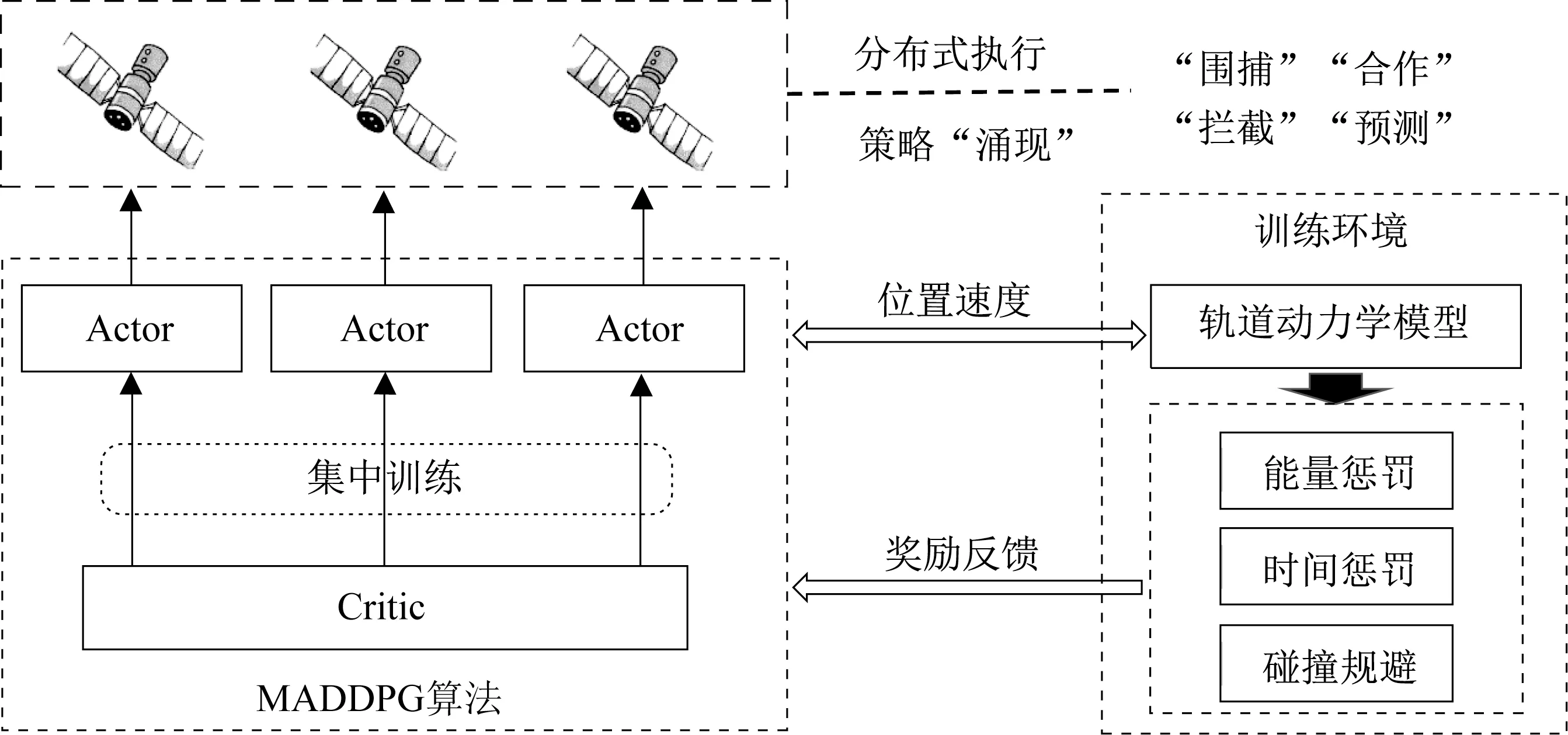
圖4 軌道追逃博弈方法實現原理Fig.4 Method of the orbital pursuit-evasion game method

首先是追捕衛星捕獲成功時的獎勵函數設計，規定捕獲的成功條件為

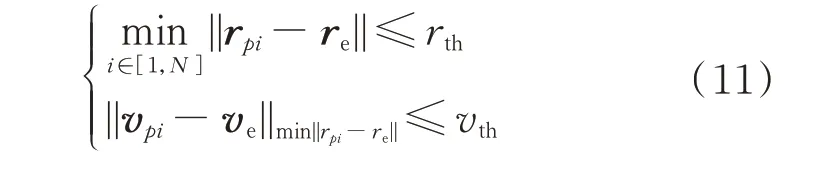
式中：第1 部分為追捕衛星中的某一顆衛星與逃逸衛星之間的距離小于等于一定的距離閾值；第2部分為當其中一顆衛星與逃逸衛星距離最近時，相對速度也小于等于一定的速度閾值，當兩部分同時滿足時，則定義為追捕博弈行為成功。

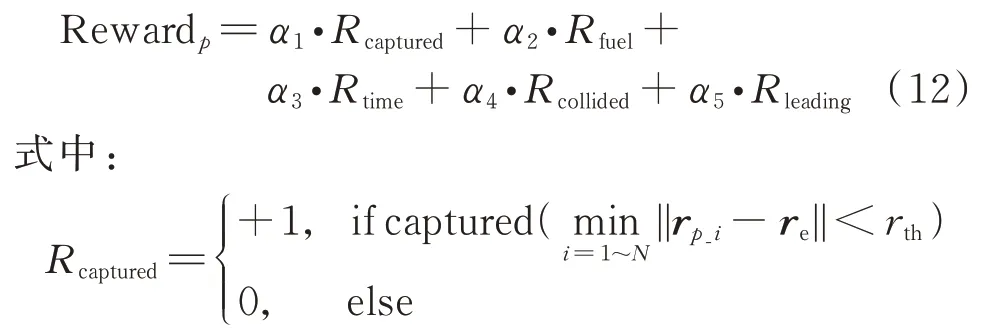
為當有其中一個衛星捕獲逃逸衛星時獲得任務正向獎勵；=-||Δ||為對衛星在追捕過程中燃料消耗的懲罰，為了防止追捕時間過長，在獎勵函數中加入了＜0，將時間作為懲罰，讓追捕衛星能夠以更快的速度捕獲到逃逸衛星，考慮到集群衛星在追捕過程中要避免碰撞；

為當集群衛星中相互碰撞后進行負獎勵作為懲罰；同時，由于稀疏獎勵可能產生不容易收斂的問題，利用強化學習獎勵塑造的方法，在博弈過程中增加引導性獎勵；

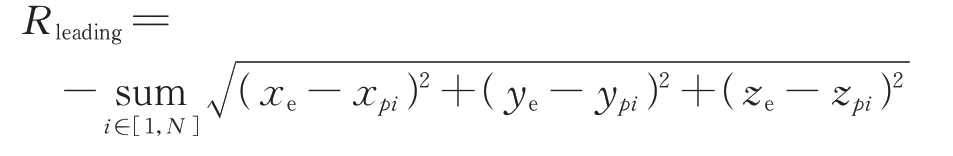
為多個智能體衛星與逃逸衛星的整體距離越小，則獎勵越大；、、、、為各獎勵的權重系數，可根據具體任務調整大小。

逃逸衛星的目的是能夠最大限度地避免被追捕衛星捕獲，因此在環境交互訓練中，逃逸衛星每一步的獎勵函數設計如下：

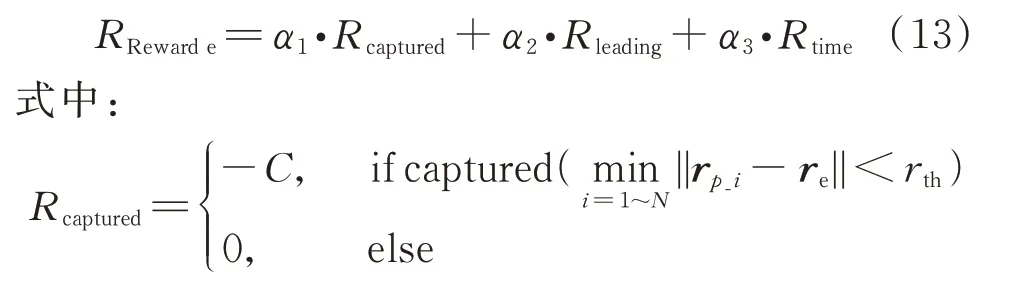
為被捕獲后的懲罰；由于只通過目標獎勵容易造成稀疏獎勵無法收斂，因此根據強化學習獎勵塑造中目標一致的原則，加入引導獎勵

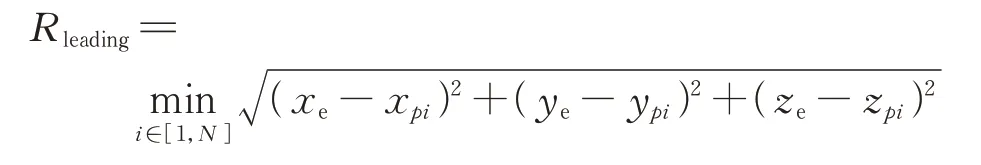
隨著與捕獲智能體愈近，給予逃逸衛星更大的懲罰；同時加入了時間獎勵＞0，表示博弈持續時間越長，智能體衛星得到的獎勵越大；、、分別為捕獲懲罰、引導獎勵、時間懲罰的權重系數，可針對不同任務進行調整。

4 MADDPG 算法

4.1 強化學習算法

本文實驗針對同步軌道的集群衛星追逃博弈場景進行了設計。假設有一個3 衛星編隊在軌道高度為42 249 137 m 附近運行（7.270 1×10），在相對坐標系500 m×500 m×500 m 空間內（訓練時位置速度隨機設定）遇到了軌道根數相似的一顆非合作目標衛星，實施追逃博弈方案。

為了使實驗更具可操作性，設定逃逸衛星機動能力比追捕衛星機動能力大，即/=1.2，同時，規定=10 m，=0.5 m/s 為距離和速度的安全約束，當其中有一個追捕衛星靠近了逃逸衛星該距離和速度的約束值內時，博弈結束，追捕成功，每次博弈時間上限為1 000 s。由于在相對軌道系下進行博弈訓練，因此在忽略高階項后系統環境滿足C-W 方程，而在C-W 方程中，耦合較為緊密的是、軸，這也是系統的復雜點，為加快收斂，忽略軸的動力學模型。假設追捕衛星和逃逸衛星均在一個軌道面運行，得到一個軌道面內二維的博弈場景。

本文實驗平臺：CPU 為intel-10500，內存8 GB×2，顯卡為GTX1660。針對以上場景進行訓練。

4.2 結果分析

通過以上的實驗設計，在合理調整獎勵函數的權重值，針對簡化后追逃博弈模型進行訓練后，算法達到了收斂。追捕衛星整體的獎勵收斂過程效果如圖5 所示。

圖5 追逃博弈訓練獎勵收斂過程效果Fig.5 Results of the reward convergence process of pursuit-evasion game training

在圖5 中，隨著博弈的進行和追逃博弈雙方策略的不斷優化，獎勵值有3 個階段的變化趨勢與特點：在一開始，博弈雙方策略均未能生成，可以理解為隨機進行博弈獎勵，由于追捕智能體具有數量優勢，因此先找到了一定的聯合策略進行優化，此階段使得追捕智能體獎勵值保持增加；隨著回合的增加，逃逸智能體逐漸利用到了機動性能的優勢，開始生成一定的逃逸策略，由于追捕智能體生成的“初級協同策略”開始失效，使得追捕智能體獎勵函數值持續下降；隨著博弈的繼續進行，追捕智能體逐漸開始針對逃逸智能體優化其協同追捕策略，而逃逸智能體也利用自身機動優勢針對追捕智能體的追捕策略進行逃逸策略的優化，因此獎勵值在不斷的波動中。最后，雙方的策略在一定范圍內實現動態平衡，得到最優或者次最優的追捕和逃逸策略。

各個智能體完成了集中訓練，分散開始執行策略時，博弈策略驗證時“涌現”出來了一系列的智能協同追逃博弈現象，主要有以下4 類，如圖6 所示。

圖6 “涌現”的智能博弈行為Fig.6 Emergent intelligent pursuit-evasion game behaviors

1）協同圍捕。“協同圍捕”現象在驗證時最為常見，典型特點為多個追捕智能體按照不同方向靠近逃逸智能體，實現對逃逸智能體的“包圍”，通過縮小范圍完成追捕策略。

2）智能攔截。“智能攔截”的現象多出現在當逃逸智能體在一個方向逃逸機動時，追捕智能體協同運動至其逃逸方向上，實現攔截，當位置速度小于閾值時使得追捕博弈成功。

3）合作追逐。“合作追逐”的場景更具可觀賞性，追捕智能體并不是單單從距離上靠近實現協同追捕，而是有計劃地在逃逸智能體的其他方向上進行運動干擾，參與追捕博弈的智能體也不單單只是實現追捕的目的，有些智能體是以合作者的身份進行博弈，最終完成協同追捕任務。

4）預測潛伏。“預測潛伏”為這樣一類場景和策略：當逃逸智能體試圖通過機動優勢“飛掠”過追捕智能體時，追捕智能體采取應對策略，先偽裝成其他方向的機動，當逃逸智能體靠近以后，再改變機動方向，實現預測和潛伏的行為，最終實現追捕博弈。

5 結束語

本文面向空間多對一非合作目標追逃博弈場景進行了調研和分析，通過對博弈場景進行建模，在考慮最短時間、最優燃料以及碰撞規避的情形下進行獎勵函數的塑造和改進，利用MADDPG 的方法進行集中訓練，得到各個追捕衛星和逃逸衛星的最優追逃策略參數；然后分布式執行，使得多個追捕衛星和逃逸衛星之間能夠完成追逃博弈。仿真結果表明，該方法能夠完成集群衛星對非合作目標的追逃博弈，且能夠利用數量優勢有效地彌補速度劣勢，涌現出“攔截”“圍捕”“潛伏”“捕 獲”等一系列智能博弈行為，有效地實現了博弈的目的，為衛星實施多對一非合作目標軌道追逃博弈的方法提供了一定的參考意義。