高軌衛星遠程抵近軌道優化研究

刁華飛，尚曉龍，王 培，蘆 雪

（1.航天工程大學，北京 101416；2.中國人民解放軍32030 部隊，新疆 和碩 841200）

0 引言

近年來，隨著高軌衛星數量的日益增加以及太空軍事化進程的加速，軌道抵近與鄰近操作（Rendezvous and Proximity Operations，RPO）正在變得越來越頻繁。RPO 包含軌道抵近和鄰近操作兩部分。其中，軌道抵近需要通過多次機動變軌，匹配與目標衛星的軌道高度、軌道平面以及在軌相位。高軌衛星處于地球同步軌道（Geosynchronous Earth Orbit，GEO）帶的不同相位上，常使用調相機動的方式達到抵近的目的。調相轉移用時一般為軌道周期的正整數倍，這使得抵近過程往往需要較長的時間。而對于任意位置、任務時間約束下的軌道攔截，基本采用基于Lambert 轉移，當進行遠程抵近時消耗燃料過多。因此，軌道抵近過程中的軌跡優化設計在高軌抵近任務中有著重要意義。遠程抵近高軌非合作目標時，往往需要大幅調整、快速響應，一般采用化學燃料的脈沖變軌。脈沖變軌的主要問題，就是研究在航天器燃料約束下，從初始軌道至目標軌道的轉移過程中，航天器施加脈沖的時機、次數以及脈沖矢量的方向和大小，這是一個非線性最優規劃的問題。

對于脈沖軌道轉移，國內外學者已經取得了許多成果。非線性交會研究多是基于不考慮攝動的二體運動學方程。當追蹤星和目標星均處于圓軌道時，若對轉移時間沒有約束，則平面內的最優交會是雙脈沖的霍曼轉移。霍曼轉移僅局限于共面圓軌道的情形，而Lambert 轉移則可以適用于任何軌道，因此Lambert 轉移方法被廣泛應用于非線性最優交會研究中。1963 年，LAWDEN基于二體模型給出了脈沖變軌的“主矢量”理論，用于確定脈沖作用下最優轉移軌道的必要條件。1968年，LION 等在LAWDEN研究 的基礎上，提出一種沖量校正理論，通過增加脈沖次數、初始漂移或減少脈沖次數實現對非最優軌跡的速度增量優化。在上述理論基礎上，不少學者對最優脈沖交會進行了深入研究，一些新的優化理論應運而生，如非線性規劃法、遺傳算法、蟻群算法、模擬退火算法、粒子群算法、差分進化算法（Differential Evolution，DE）等。文獻［10］采用非線性規劃求解固定時間內兩異面橢圓間的燃料最省的多脈沖交會問題，并對三脈沖和四脈沖方式進行軌跡優化計算；文獻［11］采用動態規劃算法求解多脈沖最優交會問題；文獻［12］采用進化算法，以燃料和時間為組合優化指標，對非固定時間的軌道轉移和攔截問題進行優化；文獻［13］采用非線性規劃算法對不同攔截時間和脈沖次數的優化情況進行了比較分析。

針對高軌衛星遠程抵近的軌道設計優化問題，本文使用Pork-chop 速度增量等高線圖對時間約束內單脈沖Lambert 轉移進行分析，而后提出一種收斂性較好的多脈沖抵近優化設計模型，使用DE 對多組算例進行全局尋優。

1 高軌轉移動力學建模

1.1 衛星在軌受力分析

對于高軌衛星而言，中心天體的引力顯然是最主要的外力源，除此之外還需考慮各種攝動力的影響，由此可建立受攝二體模型如下：

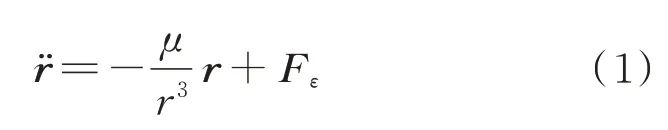
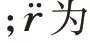
本文的研究對象是高軌衛星，在這個空間范圍內，地球大氣對衛星產生的阻力可忽略不計，這里主要考慮地球的非球形攝動力太陽。因此，本文研究所使用的軌道外推模型僅考慮含J2 項的地球非球形攝動加速度：

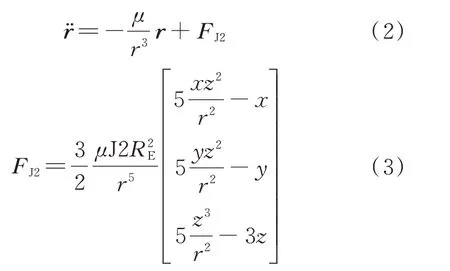
式中：為含J2 項的地球非球形攝動加速度；[]為衛星在地心慣性坐標系下的位置坐標；為地球半徑。

1.2 Lambert 轉移與求解算法

Lambert 轉移描述了2 個圓錐曲線軌道之間的固定點交會，被廣泛應用于空間軌道設計領域，適用于研究高軌抵近任務。Lambert 是關于圓軌道上任意2 個時刻的位置坐標同時間的關系定理，給定2 個位置矢量和它們之間的飛行時間，便決定其飛行軌道。Lambert 定理的數學表述為

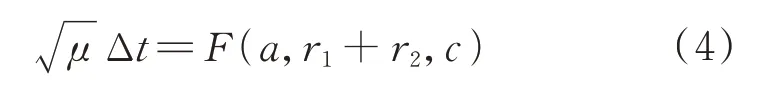
式中：為轉移軌道的半長軸；為轉移軌道始末點之間的距離；Δ為轉移時長。

歐拉和拉格朗日用解析法證明了Lambert 定理，并求得了二體模型下Lambert 問題的解析解：

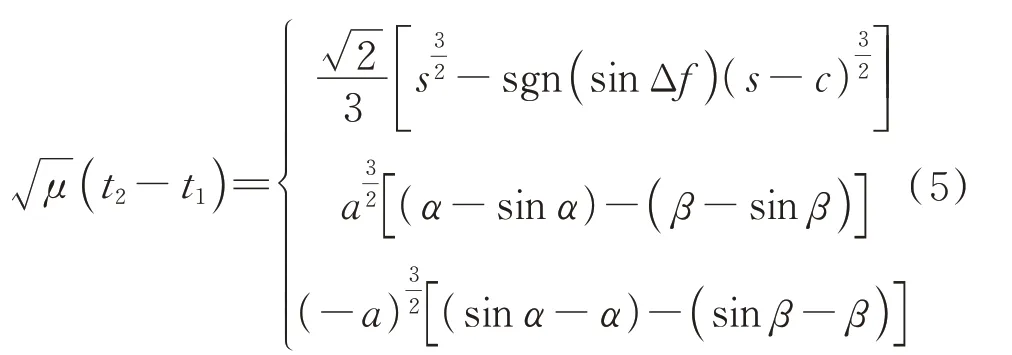
變量和由等式參數(，+，)決定，定義如下：

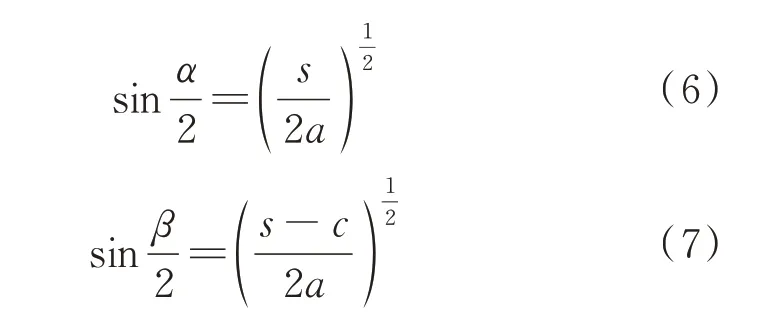
式中：變量=(++)∕2，表示三角形的周長。

Lambert 轉移基 于Lambert 定理提 出，已知2 個位置坐標和轉移時間確定飛行軌道，如圖1 所示。已知機動衛星初始點位置矢量為，速度矢量，目標星的位置矢量為，速度矢量，轉移時間為=-。根據Lambert 定理，可以求解。

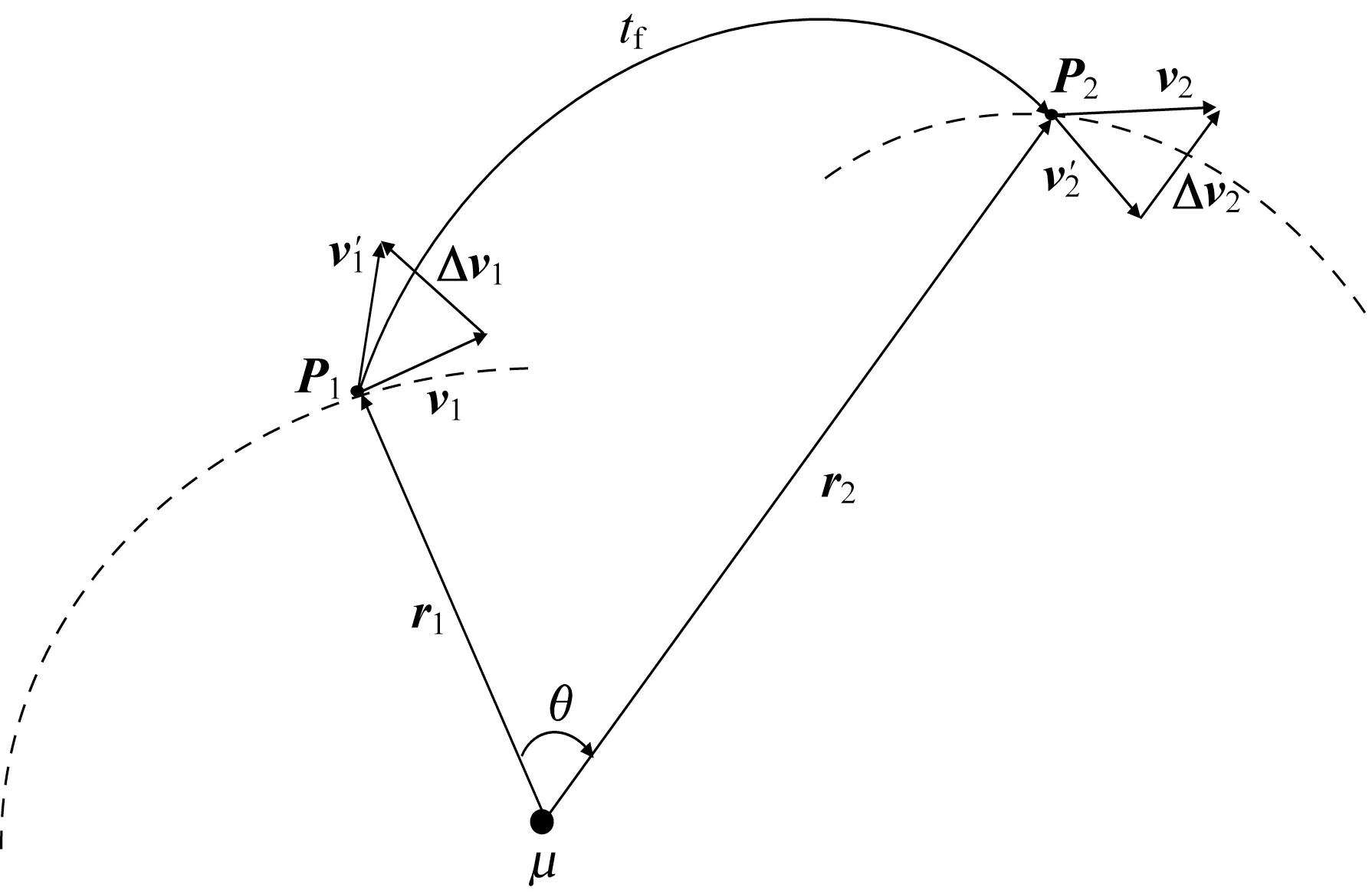
圖1 Lambert 轉移Fig.1 Schematic diagram of the Lambert transfer

進一步可得到橢圓軌道的半通徑，再由半通徑確定轉移軌道初末2 點、的速度′、′。由此計算轉移所需的速度增量為

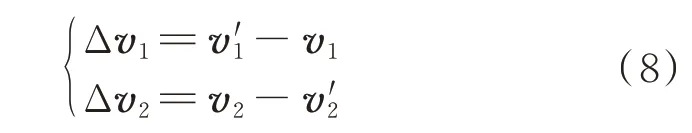
式中：Δ為機動星在時刻由原軌道進入轉移軌道的速度增量；Δ為機動衛星在時刻由轉移軌道進入目標星軌道的速度增量。

根據以上關系，建立Lambert 交會方程：

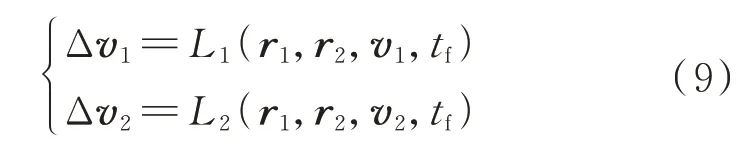
求解Lamber 問題涉及超越方程，只能用迭代法求解。Lambert 轉移的求解涉及超越方程，只能通過迭代方式求解，常用的迭代方法有Gauss 迭代法和普適迭代法。Gauss 迭代法是Gauss 在確定谷神星軌道的過程中提出來的經典方法，普適迭代法是Battin 提出的一種對3 類圓錐曲線的方法。當只考慮二體引力的情況下，求解高軌問題時軌道預報產生的誤差較大。而現有的Gauss 迭代法、Battin方法等只能解決二體模型下的Lambert 問題，無法處理攝動模型下的Lambert 交會求解。

本文以J2 項攝動模型為例，使用受攝Lambert問題的迭代求解算法，具體流程如圖2 所示。具體步驟如下：

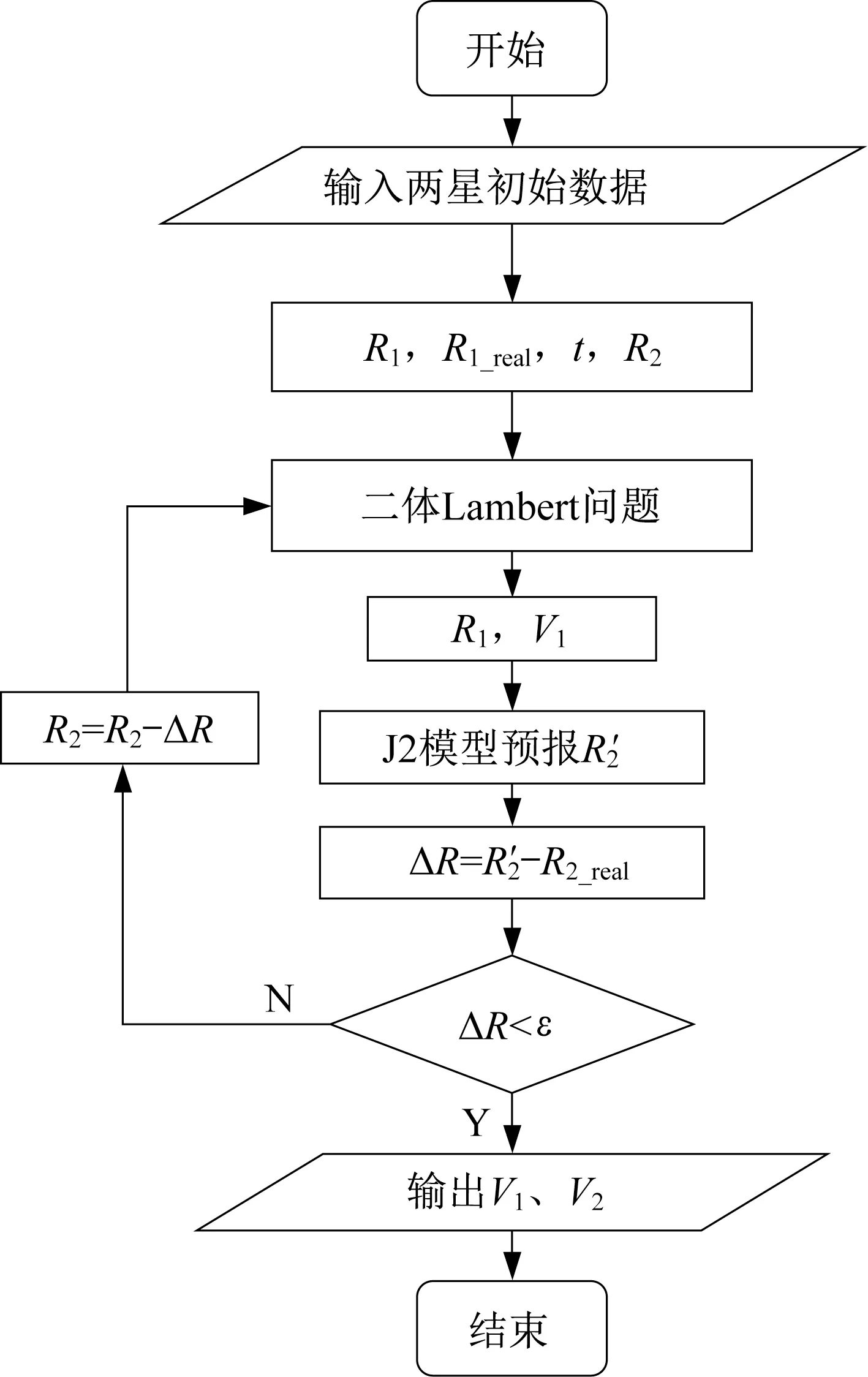
圖2 受攝模型的Lambert 問題求解算法Fig.2 Lambert solving algorithm for the perturbed model

給定轉移時間，由兩星初始數據得出起始位置、目標位置，并賦值迭代目標位置以初值=；

以Battin 方法求解二體Lambert 問題，得到初始位置的速度；

將起始位置和步驟2 得出的初始位置速度，代入J2 模型預報出轉移時間之后的衛星位置′；

由于J2 項攝動的影響，時刻衛星實際位置與目標位置存在偏差，求出終端脫靶量Δ=′-；

為了修正偏差，需要對二體Lambert 問題中的目標位置進行修正，以=-Δ作為下一次求解二體Lambert 問題的目標位置。

重復步驟1～5，直到|Δ|＜時，輸出轉移軌道起始位置和目標位置的速度、。

2 基于Pork-chop 圖的單脈沖轉移速度增量分析

2.1 Pork-chop 圖

Pork-chop圖是一種搜索軌道轉移窗口的經典方法，被廣泛應用于深空任務的設計與規劃，也可被借鑒用于高軌抵近任務的優化分析。最早由SERGEYEVSKY 等提出Pork-chop 圖，通過給定預期的機動時間和到達時間，對時間組合進行離散網格化，再針對每個二維時間點求解Lambert問題得到對應的速度增量矩陣，即可繪出Pork-chop等高圖。

Pork-chop 圖可以直觀地顯示給定時間段內速度沖量大小的變化規律，展示不同出發抵達“時間對”之間的能量對比，為任務決策提供全局參考。速度增量Δ定義為機動前后速度矢量差的模：

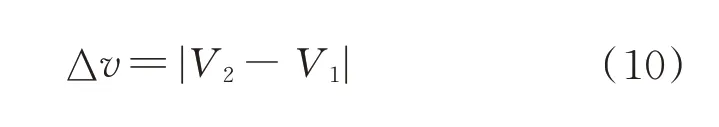
2.2 追蹤星轉移速度增量分析

對于處于理想地球靜止軌道的2 顆衛星來說，由于兩星共軌，且相對位置始終保持不變，追蹤星攔截目標星的速度增量不隨出發時間變化。星下點地理經度相差20°的2 個高軌衛星抵近的Porkchop圖如圖3所示。

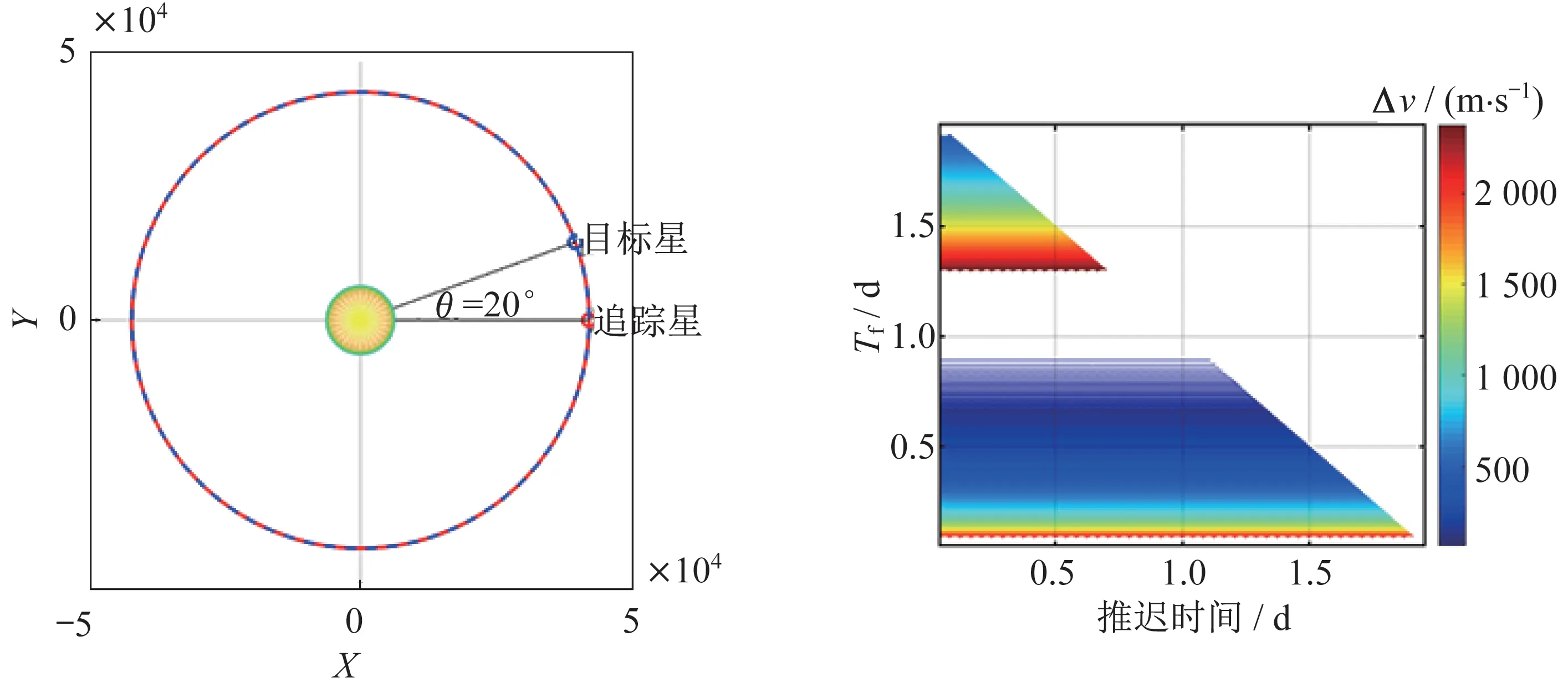
圖3 抵近理想GEO 衛星的速度增量Pork-chop 圖Fig.3 Pork-chop diagram of velocity increment when approaching the ideal GEO satellite

在圖3 中：左側繪制地慣系軌道圖，示意追蹤星和目標星初始位置；右側繪制Pork-chop 圖，橫坐標為相對初始時刻的延遲出發時間，縱坐標為抵達目標位置的軌道轉移時間；顏色條示意消耗速度脈沖的大小。圖4～圖7 解釋同上。由圖3 分析可知，地球靜止軌道衛星抵近速度增量的大小僅和轉移時間相關，與機動時刻不相關。簡單來說，在理想GEO上啟動抵近任務，任意時刻的燃料消耗都等價。

然而，非合作目標衛星往往不位于理想GEO，其偏心率和軌道傾角都會同靜止軌道存在一定偏差。假設追蹤星處于地球靜止軌道，目標星處于定位點經度與追蹤星相差20°的近地球同步軌道。以下分別選取了偏差為=0.01、=0.05、=1°、=10°等目標星軌道進行仿真分析，繪制時間約束為2 d 的Pork-chop 速度增量等高圖，如圖4～圖7所示。

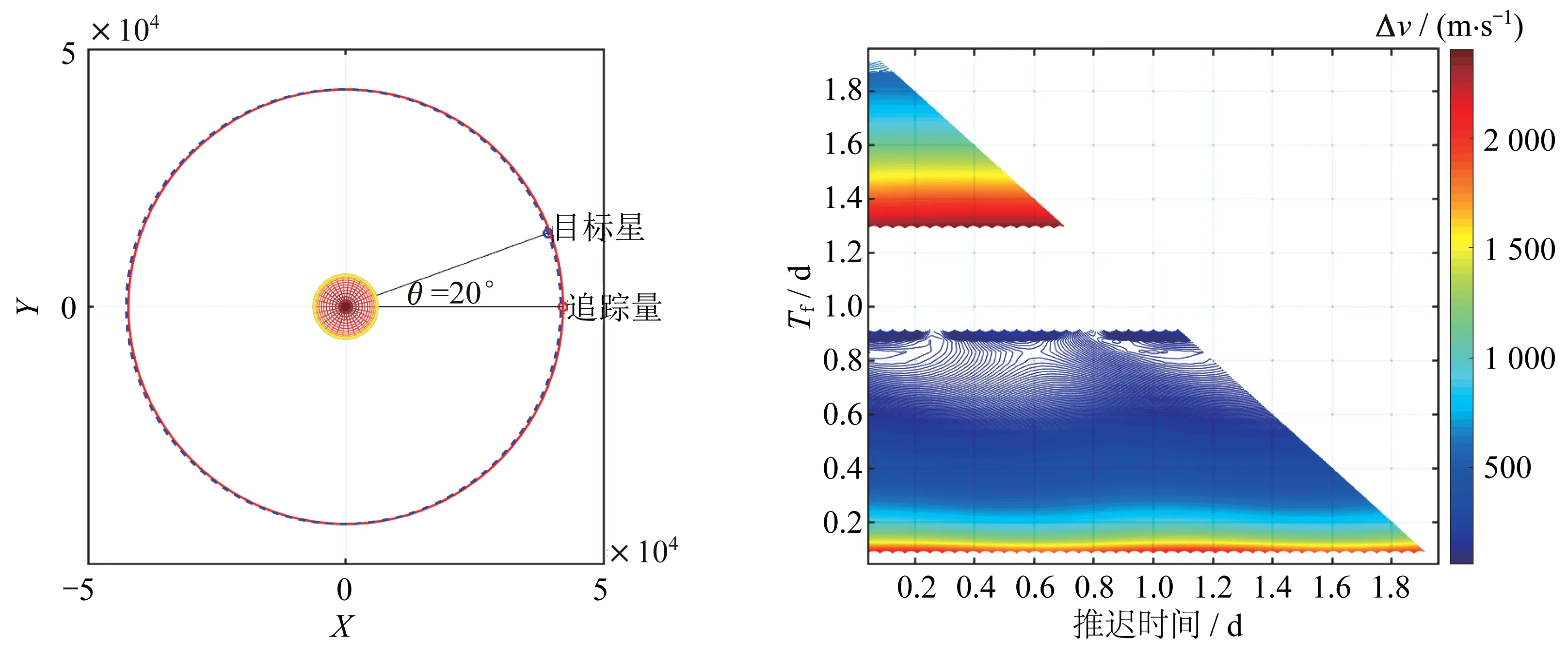
圖4 目標星e=0.01 的速度增量Pork-chop 圖Fig.4 Pork-chop diagram of velocity increment when the eccentricity of the target satellite is 0.01

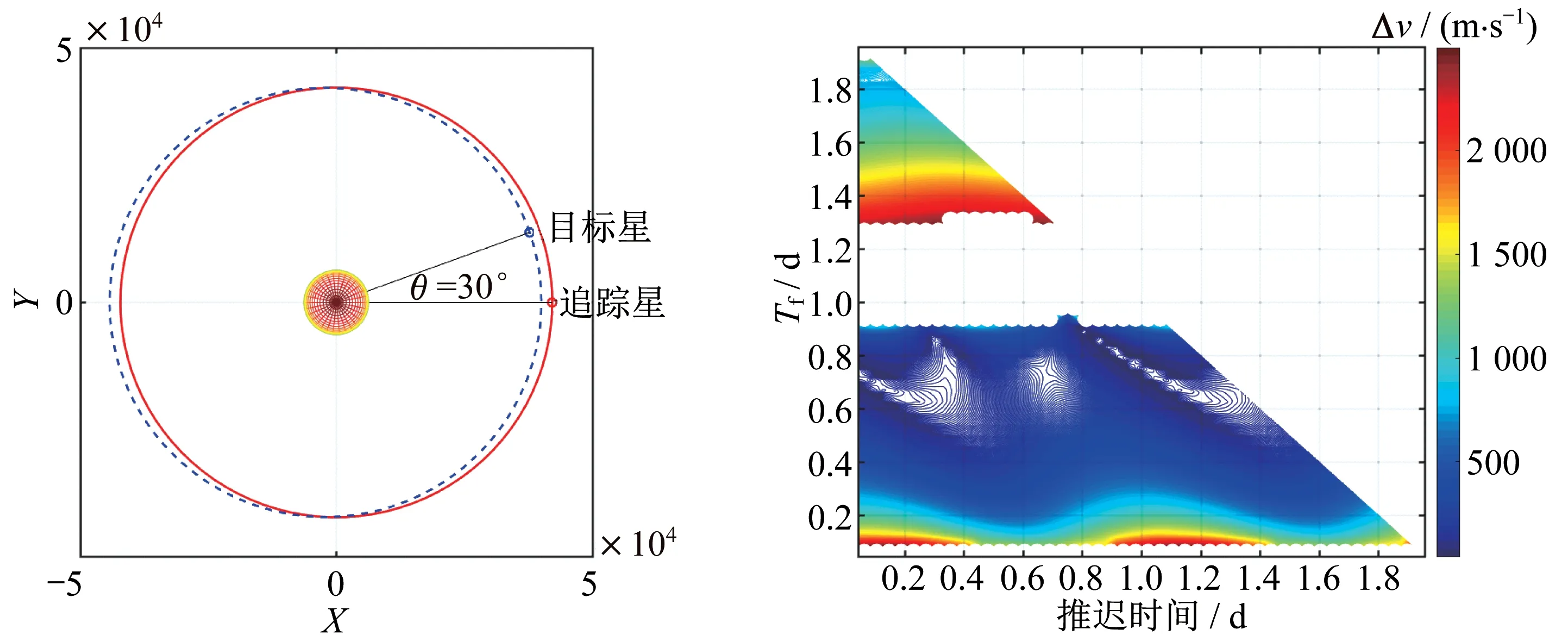
圖5 目標星e=0.05 的速度增量Pork-chop 圖Fig.5 Pork-chop diagram of velocity increment when the eccentricity of the target satellite is 0.05

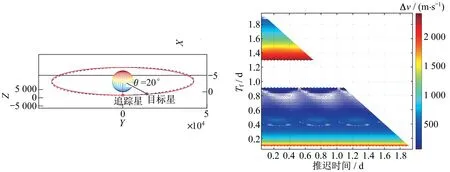
圖6 目標星軌道傾角為1°的速度增量Pork-chop 圖Fig.6 Pork-chop diagram of velocity increment when the orbit inclination of the target satellite is 1°

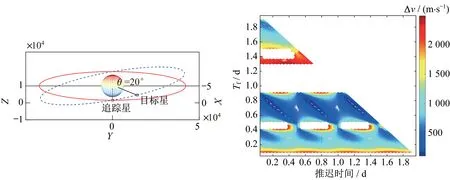
圖7 目標星軌道傾角為10°的速度增量Pork-chop 圖Fig.7 Pork-chop diagram of velocity increment when the orbit inclination of the target satellite is 10°

可見，當目標星軌道的偏心率或軌道傾角相對靜止軌道存在偏差時，最優機動時刻周期性復現規律。該周期為0.5 d，即半個軌道周期。在執行高軌抵近任務時，由于不存在絕對理想的地球靜止軌道衛星，任務時間約束內，追蹤星何時機動，何時抵達最優，在時間上并不均勻。

3 多脈沖抵近優化設計

3.1 多脈沖抵近的數學模型

多脈沖抵近就是通過在轉移過程中多次點火施加速度脈沖的方式，使衛星從初始軌道上的一點轉移到目標附近打靶點的抵近方式。本節以三脈沖抵近為例進行建模，整個抵近過程如圖8 所示。

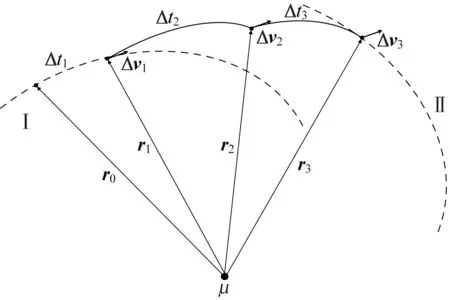
圖8 三脈沖抵近Fig.8 Schematic diagram of triple-pulse proximity

假設追蹤星位于初始軌道Ⅰ，目標星位于其運行所在的軌道Ⅱ。任務起始時刻，追蹤星在地慣系下的空間位置為。經Δ的無動力滑行，至空間位置，第一次點火施加速度脈沖Δ。經Δ的無動力滑行，至空間位置，第二次點火施加速度脈沖Δ。再經Δ的無動力滑行，至目標星附近打靶點位置，實現抵近。最終通過第三次點火施加速度脈沖Δ，進入目標軌道。定義首次速度脈沖Δ為起漂脈沖，末端速度脈沖Δ為剎車脈沖，首末之間的速度脈沖Δ為中間脈沖。已知Ⅰ、Ⅱ軌道參數、任務起始時間和目標附近打靶點，當確定了Δ、Δ、Δ，由于衛星按照式（2）在空間中運行，、、可通過軌道積分確定。當確定了中間脈沖點，通過2.3節方法求解Lambert 問題可得出脈沖Δ、Δ。根據給出的目標附近打靶點參數可求出脈沖Δ。故三脈沖抵近要確定的獨立變量有3 個滑行時間以及1 個3 自由度的中間脈沖點坐標，共6 個獨立變量。

基于以上分析推廣，對于給定目標附近打靶點的脈沖轉移問題，轉移過程中包含1 個起漂脈沖Δ，-2 個中間脈沖Δ，Δ，…，Δv，以及1 個剎車脈沖Δv。故脈沖抵近要確定的獨立變量有個漂移時間Δ，Δ，…，Δt以及-2 個3 自由度中間脈沖點坐標，，…，r，共4-6 個獨立變量。

然而，考慮到3 自由度中間脈沖點坐標搜索區間范圍過于龐大，導致模型的優化求解難以收斂。本文提出虛擬Lambert 滑行拼接的方法解決該問題。以三脈沖轉移為例，尋中間脈沖點時，首先求解漂脈沖位置和剎車脈沖位置在Δ+Δ時間區間內的Lambert 問題，虛擬遞推該軌道，并在時刻Δ處取點，作半徑為Δ的中間脈沖點尋優域。如此便將中間脈沖點范圍很大的地慣系坐標，，…，r，轉換為范圍較小的相對坐標Δ，Δ，…，Δr，有利于優化算法收斂。中間脈沖點尋優域如圖9所示。

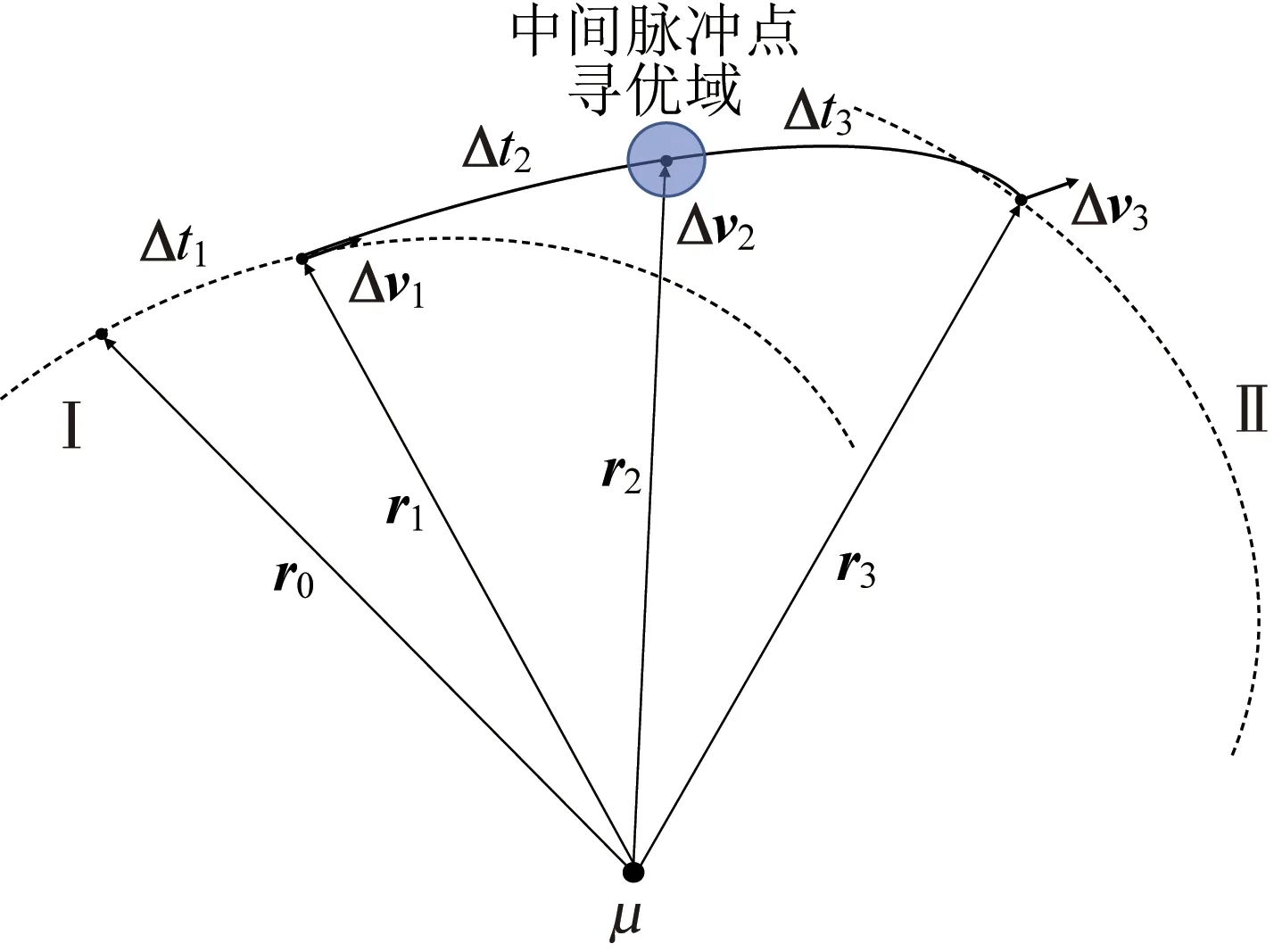
圖9 中間脈沖點尋優域Fig.9 Schematic diagram of the optimizing domain for the middle pulse point

3.2 約束條件與性能指標

高軌衛星抵近任務中要考慮以下各種約束。

3.2.1 運動狀態約束

追蹤星在脈沖位置之間按照式（2）運行。以為追蹤星狀態矢量（3 個位置量和3 個速度量），將式（2）表示(，)，則在脈沖點（包括初始位置和抵近打靶點）之間的運動狀態約束可表示為

3.2.2 時間約束

假設任務從起始時刻開始，必須在時間約束Δ內完成抵近。每次施加速度脈沖后的漂移時間（包括起漂脈沖前的等待時間）滿足約束：

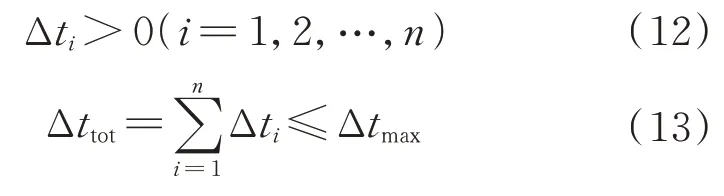
3.2.3 能量約束

追蹤星攜帶燃料有限，假設一次抵近任務所能耗費的最大速度脈沖為Δ，則抵近過程中施加的速度脈沖滿足約束：

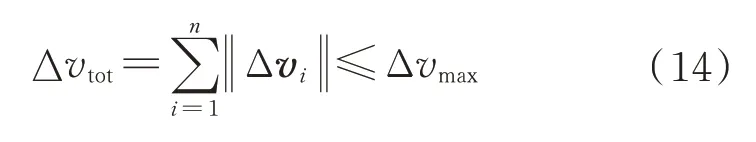
3.2.4 性能指標

以能量消耗最小作為性能指標，表示為

綜合以上約束，多脈沖抵近軌跡優化設計的數學模型表示為

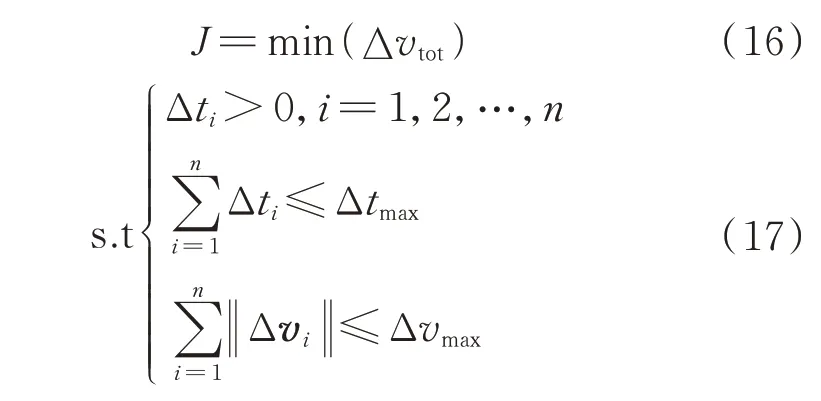
3.3 差分進化算法（DE）

DE由Storn 和Price于1995年首次提出，主要用于求解實數優化問題。該算法是一類基于群體的自適應全局優化算法，屬于演化算法的一種，具有結構簡單、容易實現、收斂快速、魯棒性強等特點。DE 的基本思想如下：從一個隨機生成的初始種群開始，將種群中任意2 個個體的向量差加上第3 個個體的和生成新的個體，然后將這個新的個體與種群中相應的當代個體相比較，如果新個體的適應度優于當前個體的適應度，則是在下一代個體中取新替換舊，或仍保持舊個體。通過不斷的進化，可以保留好的個體，淘汰差的個體，引導搜索接近最優解。其具體進化步驟如下：

首先確定DE 的控制參數，確定其適應度函數。DE 控制參數主要包括：種群大小、縮放因子與交叉概率；

隨機產生初始種群；

根據適應度函數對初始種群進行評價，計算種群中個體的適應度函數值；

判斷終止條件或進化代數是否達到最大，若是則停止進化搜索，將搜索到的最佳個體作為最優解進行輸出，若否則繼續進化；

進行變異和交叉操作，得到中間種群；

在原種群和中間種群中選擇個體，得到新一代種群；

進化代數=+1，轉步驟4。

在DE 的主要控制參數中，種群規模在算法中主要反映了種群信息的大小。值越大，種群信息越豐富。但結果會使計算量變大，不利于求解。相反，種群多樣性是有限的，這不利于算法獲得全局最優解，甚至導致搜索停滯。交叉概率主要反映后代與父代之間以及交叉過程中中間變異個體之間的信息交換量。值越大，信息交換程度越高。相反，如果值過小，種群多樣性會迅速下降，不利于整體優化。與相比，縮放因子對算法性能的影響更大，主要影響算法的全局優化能力。越小，算法的局部搜索能力越好。

4 仿真算例

假設任務起始時間為UTC 時2021 年4 月1 日12：00：00.000，追蹤星和目標星都處于近地球靜止軌道。任務初始時刻，追蹤星和目標星的瞬時軌道根數如下：

式中：為近地點幅角；為升交點赤經；為真近點角。

不考慮入軌相對構型，假設以目標星位置作為打靶點，目標星軌道作為打靶軌道，分別對不同時間約束下的雙脈沖抵近、三脈沖抵近和四脈沖抵近進行軌道優化求解。設置DE 的種群規模=12，縮放因子=0.85，交叉概率=0.85。設置最大迭代次數為100，并對每組輸入數據進行5 組優化計算實驗。當任務時間約束分別為12、24、48 h 時，仿真結果見表1～表3。24 h 時間約束下的雙脈沖抵近、三脈沖抵近和四脈沖抵近的軌跡圖如圖10～圖12 所示。

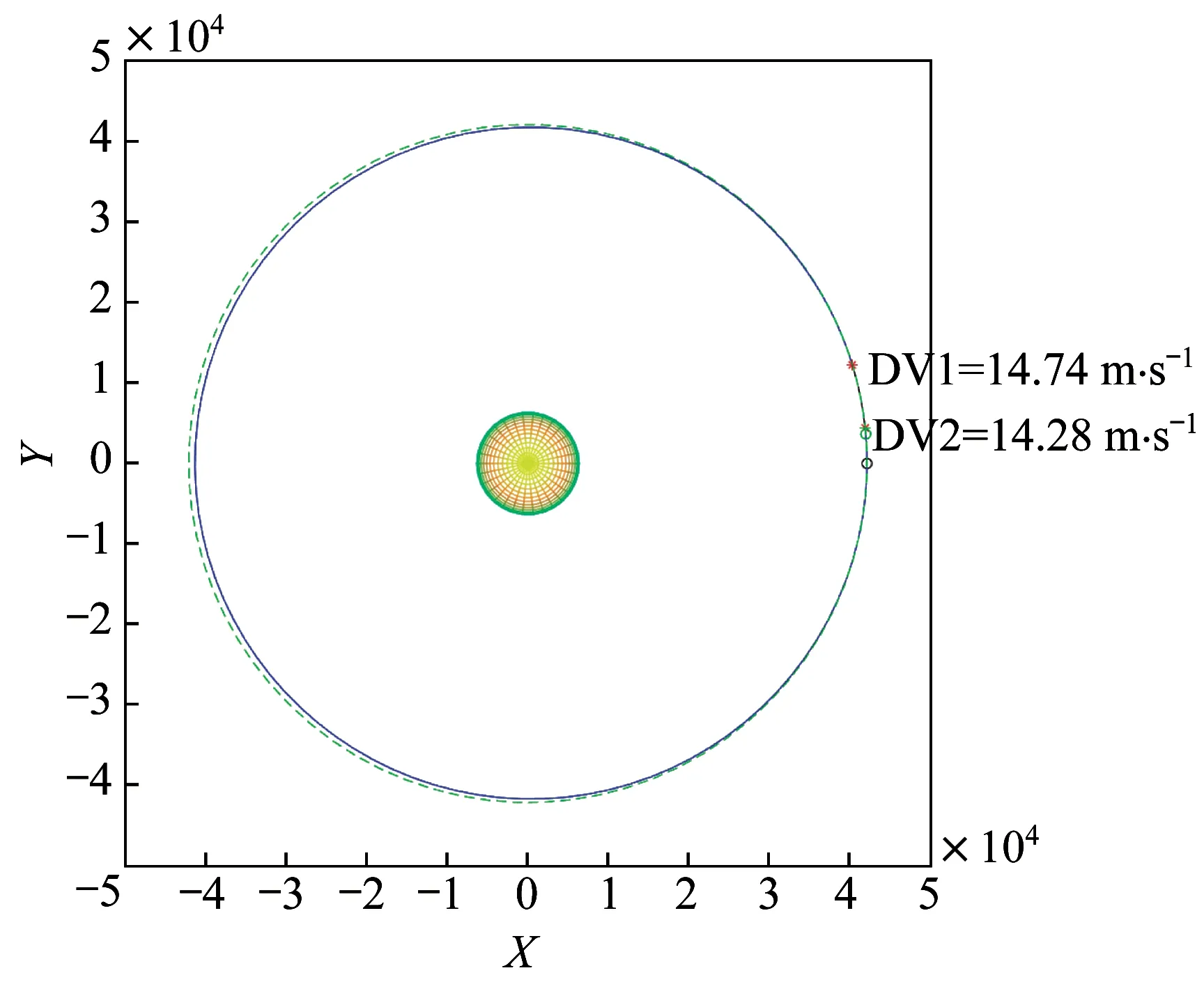
圖10 24 h 約束下雙脈沖抵近優化算例Fig.10 Schematic diagram of the dual-pulse proximity optimization example under the 24 h constraint

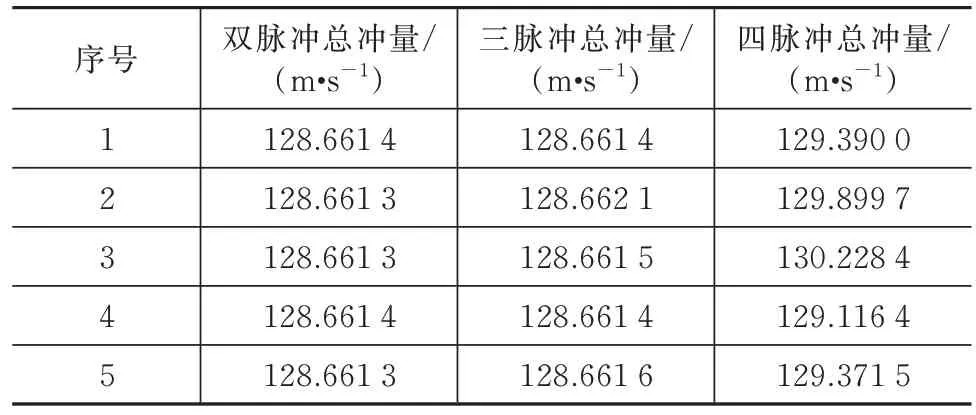
表1 12 h 約束的仿真數據Tab.1 Simulation data under the 12 h constraint

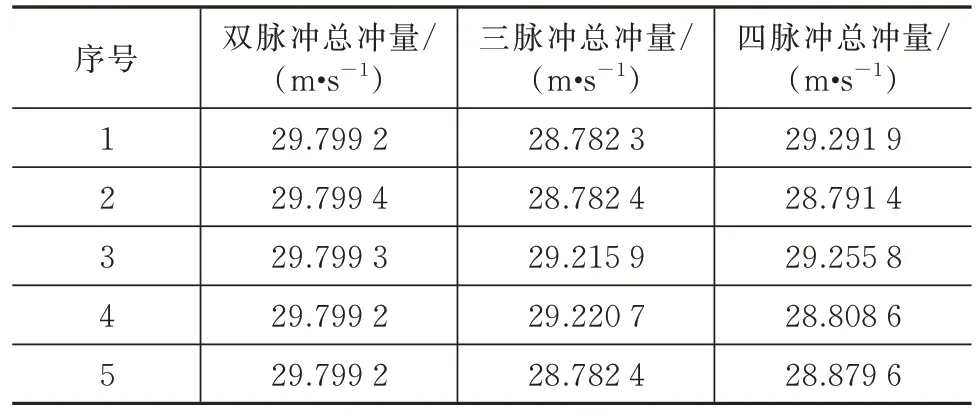
表2 24 h 約束的仿真數據Tab.2 Simulation data under the 24 h constraint

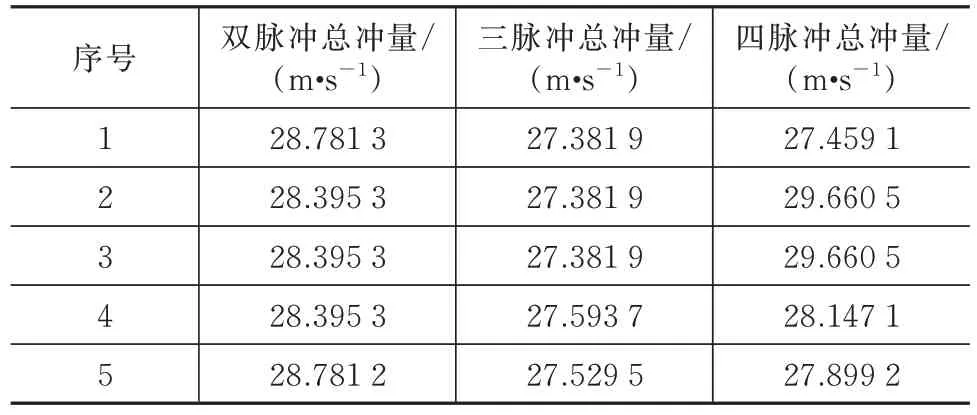
表3 48 h 約束的仿真數據Tab.3 Simulation data under the 48 h constraint

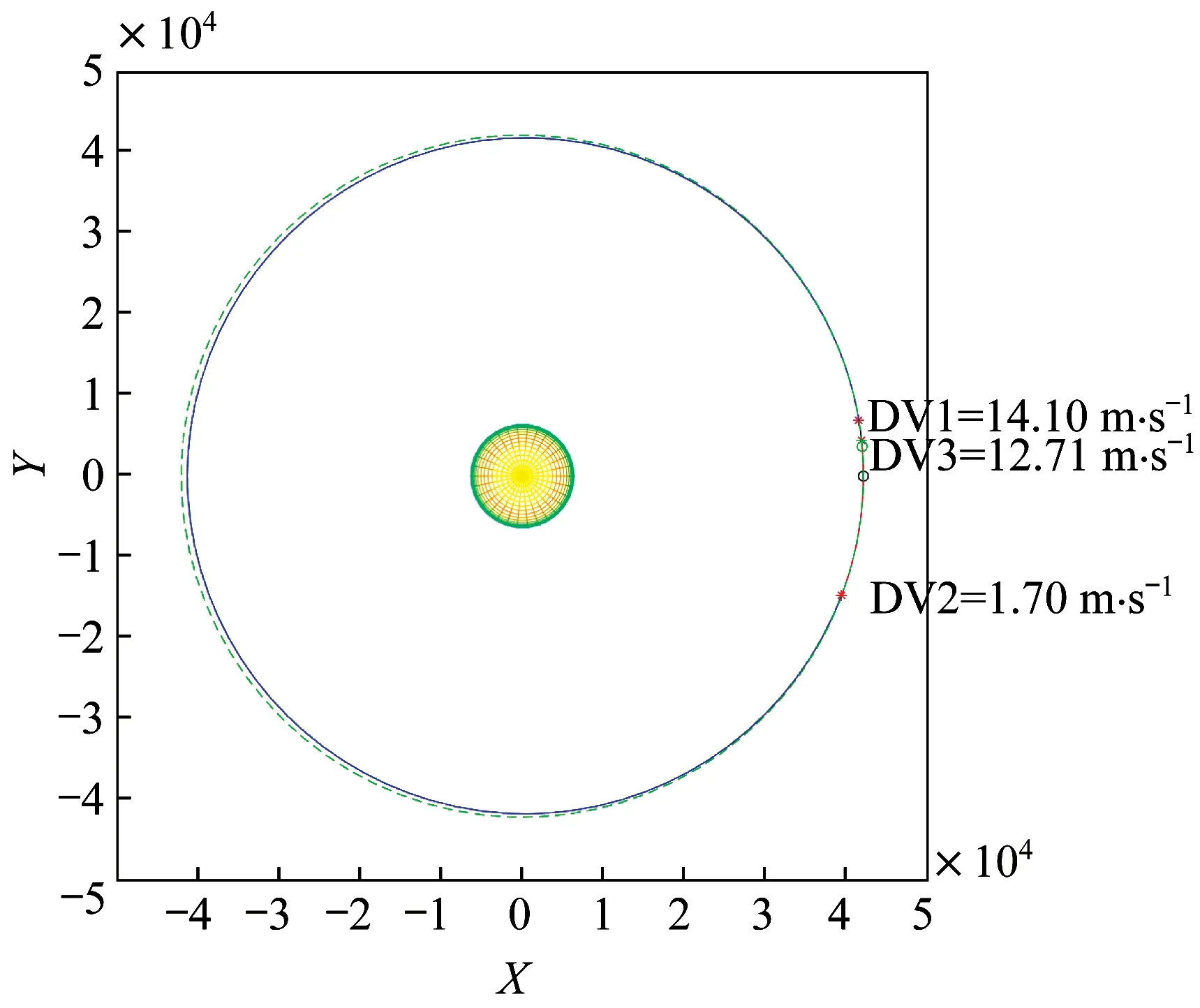
圖11 24 h 約束下三脈沖抵近優化算例Fig.11 Schematic diagram of the triple-pulse proximity optimization example under the 24 h constraint

圖10～圖12 中標注的DV1、DV2、DV3 和DV4分別指第1 次脈沖大小、第2 次脈沖大小、第3 次脈沖大小和第4 次脈沖大小，對應紅色星號示意施加脈沖的位置。

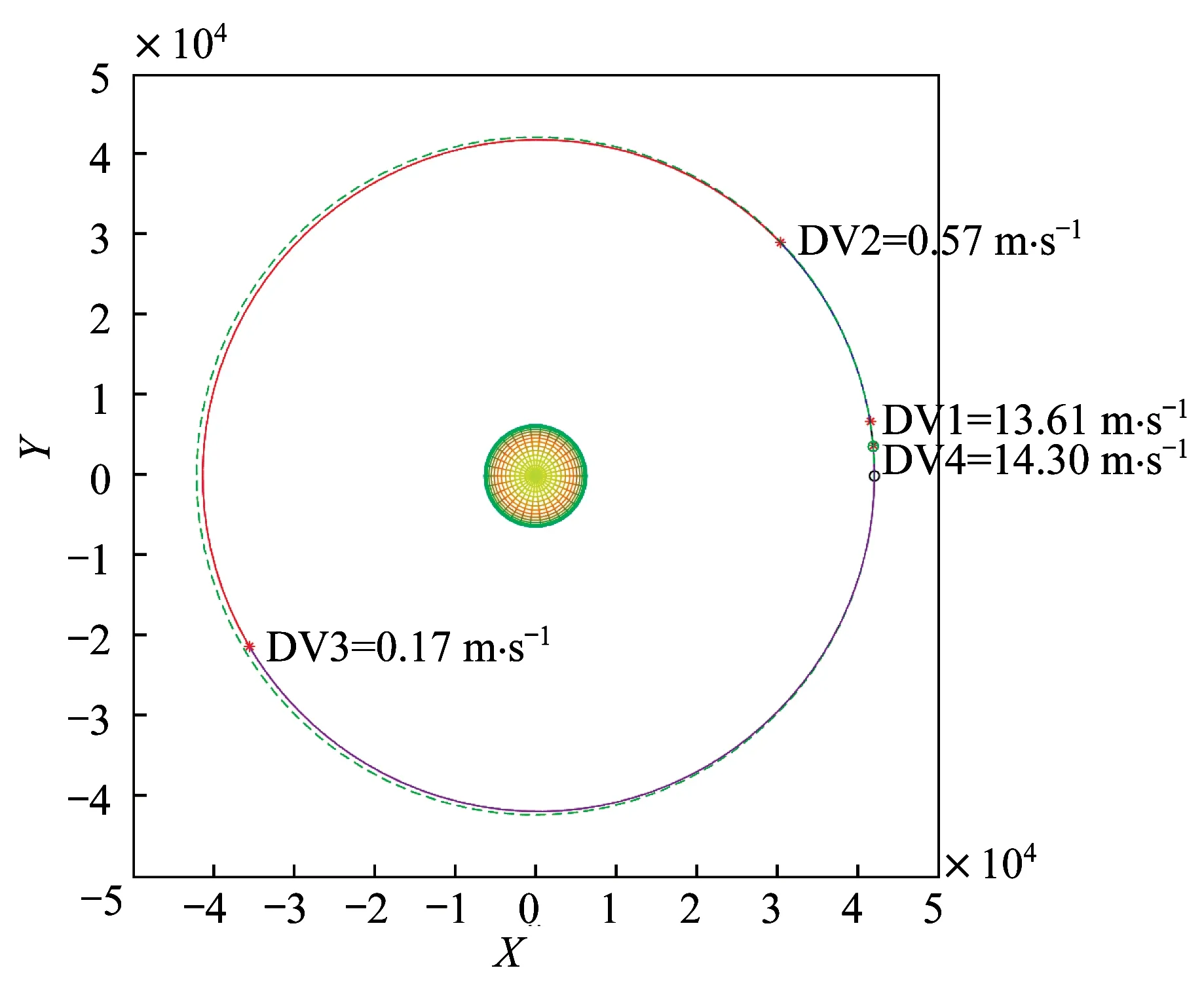
圖12 24 h 約束下四脈沖抵近優化算例Fig.12 Schematic diagram of the quadruple-pulse proximity optimization example under the 24 h constraint

由以上算例可以總結出：1）延長任務約束時間可以有效降低總沖量；2）三種脈沖次數的轉移方式的優化結果，耗費總沖量相差較小；3）在中短期抵近任務中，雙脈沖轉移由于獨立變量少所以最優解穩定易得，四脈沖轉移優化收斂性較差，而三脈沖轉移優化效果相對較好。

5 結束語

本文對高軌衛星遠程抵近問題建立了數學模型，使用Pork-chop 圖探討了非理想地球靜止軌道偏心率和軌道傾角偏差對攔截速度增量的影響，分析了任務時間約束內遠程抵近軌道最優解的分布規律。給出多脈沖抵近問題涉及的獨立變量、約束條件和目標函數，建立了多脈沖抵近軌道優化設計的數學模型。最后使用DE，通過多組算例對該問題進行優化求解，得出三脈沖抵近方案在中短期任務中優化效果相對較好的結論。