基于試驗設計-遺傳算法的開關電磁閥響應特性優化*

李紅 謝鼎盛 張澤涵 儲江偉

（東北林業大學，哈爾濱 150040）

主題詞：開關電磁閥 動態響應特性 試驗設計 遺傳算法

1 前言

機械直連的液壓制動系統已無法滿足汽車電動化、智能化的發展要求。線控制動系統的制動踏板不直接通過液壓回路與車輪制動分泵相連，能夠實現再生制動能量回收。作為線控制動系統的關鍵部件，開關電磁閥的性能直接影響汽車的制動效能。文獻[3]利用新型材料設計了一種菱形位移放大結構式驅動器，可有效控制電磁閥開啟及關閉時間。文獻[4]、文獻[5]研究了控制電路在不同驅動策略下開關電磁閥的流量響應特性，多路混合驅動、復合脈沖寬度調制（Pulse Width Modulation，PWM）控制策略可以改善電磁閥開關響應特性，但高頻驅動電壓使線圈溫度場發生變化，導致內阻波動。文獻[2]、文獻[6]利用電流精確控制電磁閥開度，實現電磁閥流量非線性的可控性，但小電流驅動狀態下，閥口流量波動較大。針對高速開關閥流量控制存在的死區和飽和區，文獻[7]利用脈寬調制和脈頻調制方式實現流量的線性化。文獻[8]、文獻[9]分別利用粒子群優化算法和智能PWM控制算法實現了電磁閥的快速開關特性及電磁線圈的低能耗要求。

上述文獻幾乎都是從新型材料驅動器或智能驅動策略角度改善電磁閥的動態響應特性，本文結合設計經驗建模，從試驗設計角度研究電磁閥動態特性，以某車型適配的一款常開電磁閥為研究對象，建立其AMESim模型，并利用開關電磁閥響應測試臺驗證所建模型的有效性，基于建立的AMESim 模型，明確電磁閥閥芯動作機理，利用控制變量法分析彈簧剛度、線圈電阻及閥芯總質量對流量特性的影響，提出一種基于試驗設計-遺傳算法的優化方法，有利于改善電磁閥動態響應特性。

2 計算模型建立

2.1 高速開關電磁閥模型

高速開關電磁閥由閥芯、閥座、動鐵、靜鐵、回位彈簧、隔磁管、密封圈等零件組成，是線控液壓系統中工作特性最復雜的元件，如圖1所示。常開式電磁閥通電時，閥芯及動鐵在彈簧力、液壓力、電磁力和摩擦力作用下下移，進、出油口關閉；斷電時，閥芯及動鐵在彈簧力及摩擦力作用下上移，進、出油口連通。常閉式電磁閥工作原理類似，其區別是通電時電磁閥打開。

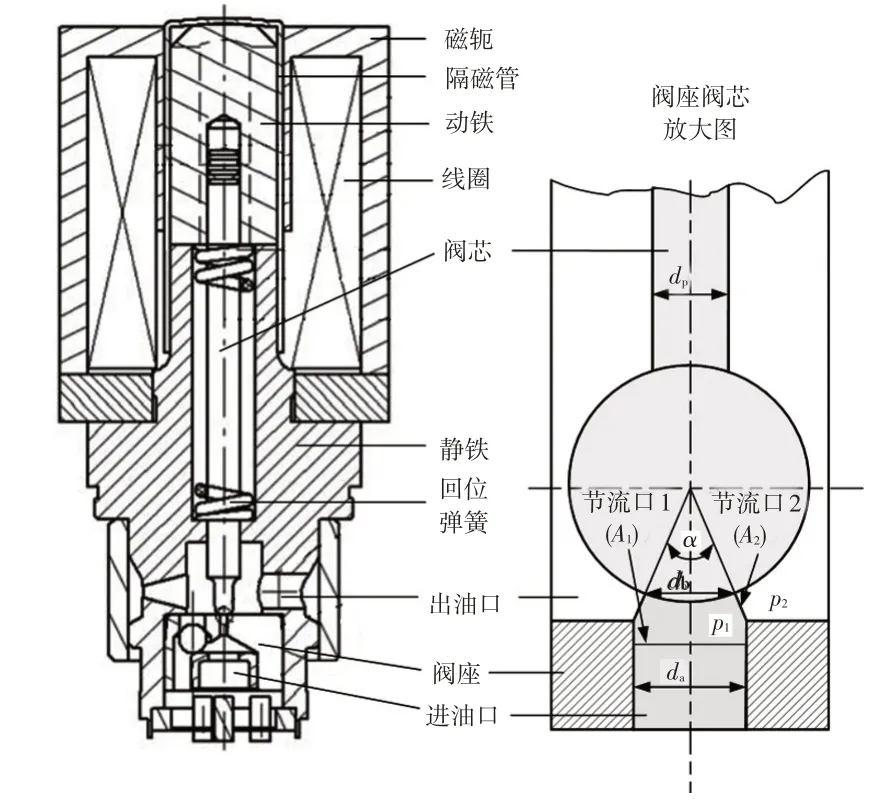
圖1 開關電磁閥結構

2.1.1 電磁力

電磁閥線圈通入電流后產生電磁力，通過插值法實時計算電磁閥電磁力，利用有限元方法獲得了電流-閥芯位移-電磁力的關系，如圖2所示。

圖2 電磁力-閥芯位移-電流關系

電磁閥線圈的電壓求解公為：

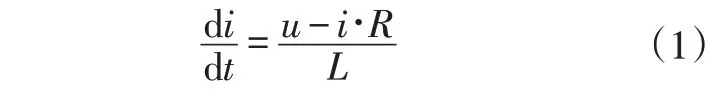
式中，為線圈電壓；為線圈電阻；為線圈電感。

2.1.2 液體作用力

閥芯工作中受到的液體作用力包括液壓力和沖擊力，在其求解過程中以圖1進油口中制動液為控制對象，其內、外的壓力分別為、，液壓力為：

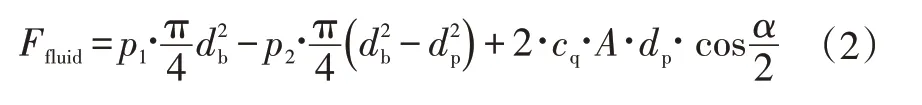
式中，為的有效作用面積直徑；為閥桿直徑；為流量系數；min{,}為過流面積；、為節流口1、2處的面積；為流向角。

2.2 動鐵及閥芯的運動學方程

線圈不通電時，閥芯處于最大位移處。通電后，電磁閥閥芯及動鐵在彈簧力、液體作用力、滑動摩擦力及電磁力作用下運動，運動學方程為：

其中，摩擦力為：

式中，為閥芯及動鐵質量；為回位彈簧剛度；為彈簧預壓縮量；為閥芯動摩擦力；為阻尼系數；為閥芯位移。

3 電磁閥AMESim模型驗證

3.1 測試系統

鑒于AMESim 中所有的模型都經過了嚴格的測試和試驗驗證，本文基于AMESim軟件建立了開關電磁閥的物理模型。以某車型適配的一款常開電磁閥為研究對象搭建了測試平臺，驗證所建物理模型的有效性。開關電磁閥響應特性測試臺如圖3 所示，由電磁閥閥體、輪缸、壓力傳感器、直流電源、傳感器供電電源及上位機組成。

圖3 開關電磁閥響應特性測試臺

3.2 測試過程

利用直流電源控制電磁閥線圈通電電流，開關電磁閥響應特性測試流程如圖4所示。

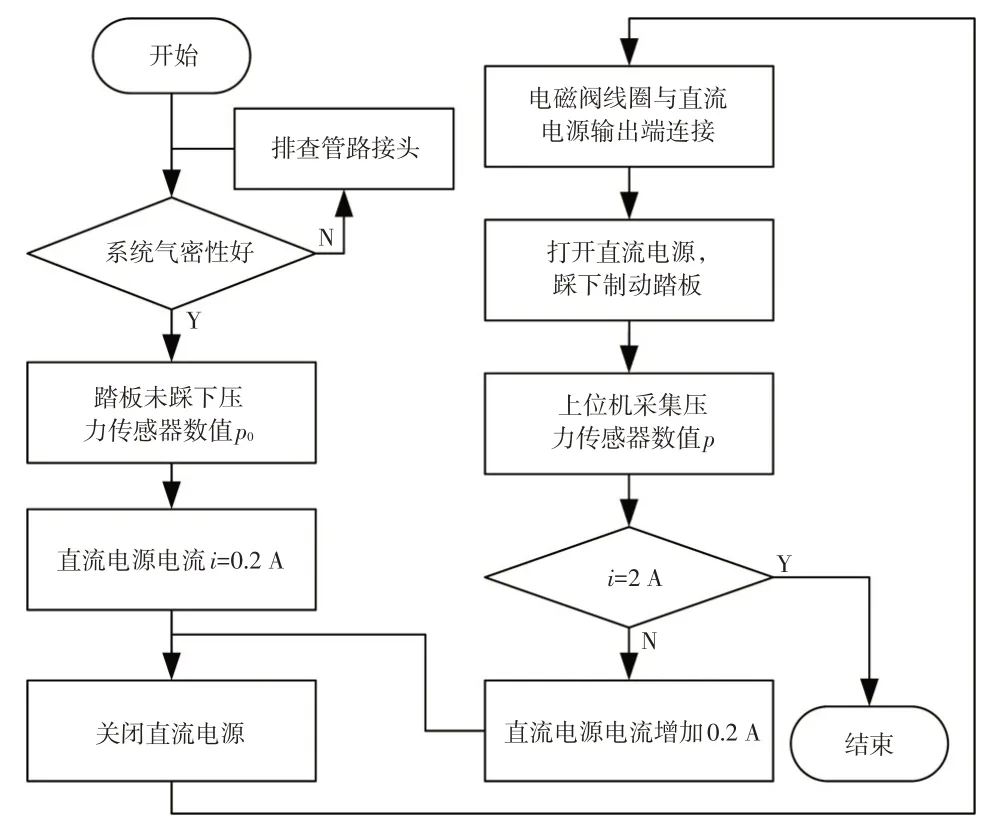
圖4 測試流程

3.3 結果分析

試驗過程中：直流電源電流設定為0.6 A時，踏板克服空行程后無法踩下，此時上位機采集的壓力傳感器讀數為13 kPa；直流電源電流設定為0.4 A 時，踏板可踩下，此時壓力傳感器讀數為335 kPa。上述數據表明，電磁閥線圈給定電流值在0.4～0.6 A范圍內某一數值時電磁閥關閉。根據測試流程，重新設定直流電源電流初始值和增量分別為0.401 A、0.001 A，直到傳感器壓力約等于，該電流即為電磁閥關閉需求電流，表1 記錄了直流電源電流設定值為0.591～0.598 A時壓力傳感器測量的電磁閥出口壓力。

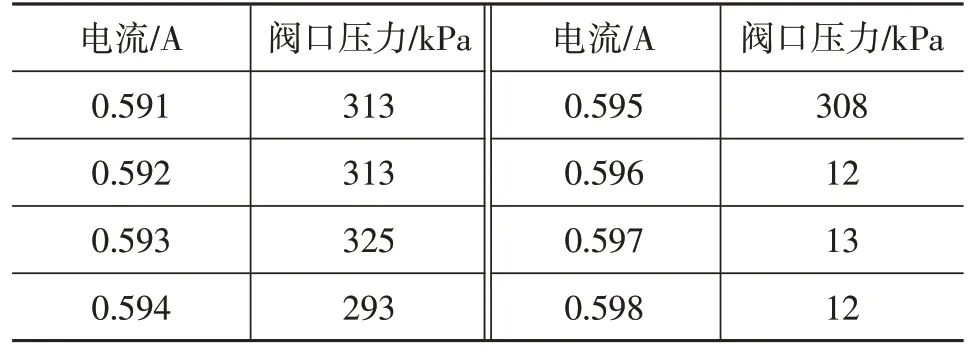
表1 開關電磁閥出口的壓力

仿真模型中電磁閥的出油口直接與油箱相連，采集的是電磁閥出口流量，電磁閥線圈通電電流由0.595 A增大到0.596 A時，閥口流量由0.790 L/min 降低到0，此時電磁閥關閉。由表1 可知，線圈通入電流增大到0.596 A時，閥口壓力降為12 kPa。上述數據表明，基于AMESim軟件建立的常開電磁閥模型有效。

4 電磁閥流量特性分析

4.1 閥芯動作機理

以建立的常開式電磁閥AMESim模型為基礎，分析電磁閥閥芯動作機理，電磁閥結構參數如表2所示。

表2 開關電磁閥參數

為了研究電磁閥參數對出油口流量特性的影響，假設電磁閥進油口壓力為1 MPa，控制電路給定周期為0.2 s 的PWM 信號，電磁閥閥口流量特性曲線如圖5所示。

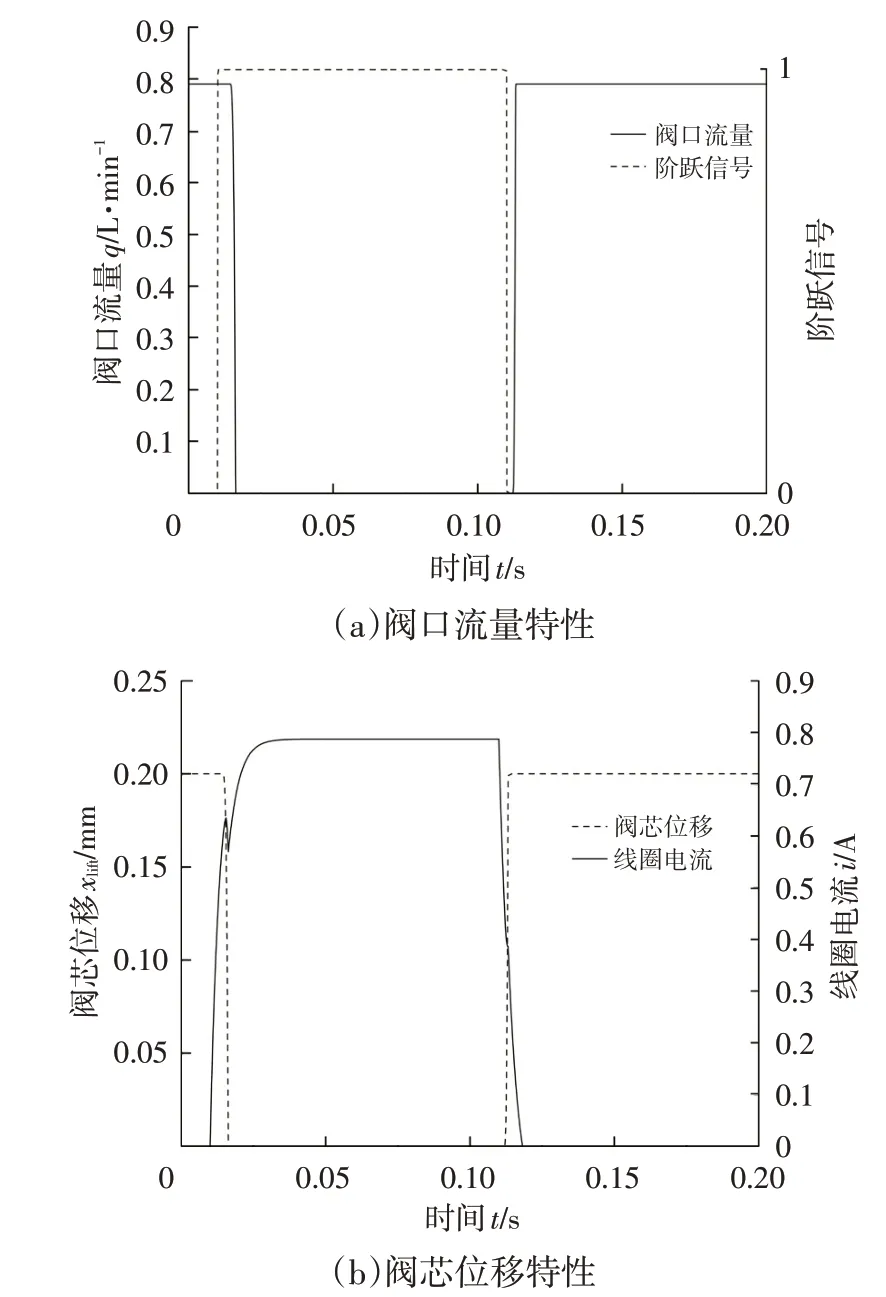
圖5 開關電磁閥閥口特性曲線

第0～0.01 s范圍內，控制電路信號給定值為0，閥芯處于最大位移處，閥口流量為0.79 L/min。第0.01～0.11 s范圍內，電磁閥給定信號值為1：由于線圈電感的作用使得第0.01～0.014 4 s 內線圈電流逐漸增大，但此時電磁力不足以克服阻力使閥芯運動，閥芯仍處于最大位移0.20 mm 處，閥口流量無變化；第0.014 4～0.016 5 s 內閥芯位移由0.20 mm 減小至0，工作氣隙的變化使線圈內產生反電動勢，線圈電流減小，直到閥芯完全落座后反電動勢降為0，隨后線圈電流繼續增加。第0.11～0.20 s時間段內，控制電路信號給定值為0，線圈內電流逐漸減小：第0.11～0.111 9 s內，閥芯受到的電磁力大于彈簧預緊力，閥口流量仍為0；第0.111 9～0.113 9 s 內，彈簧預緊力與電磁力合力推動閥芯遠離閥座，當閥芯位移由0 增大到0.20 mm 時，電磁閥完全打開，閥口流量達到0.79 L/min。

4.2 結構參數對閥口流量的影響

忽略電磁閥運行環境差異的影響，由式（3）可知，電磁閥的彈簧特性、閥本體結構及電磁部分均會對閥口流量特性產生影響。本文提取彈簧剛度、閥芯動鐵總質量及線圈電阻3個參數，利用控制變量法研究閥口的流量特性。控制變量法是在蒙特卡洛方法中用于減小方差的一種技術方法，可通過對已知量的了解減少對未知量估計的誤差。本文采用單一變量控制法對不同彈簧剛度、閥芯動鐵總質量及線圈電阻條件下閥口流量隨時間變化的特性進行仿真。

設電磁閥進油口壓力為1 MPa，閥芯動鐵總質量為3.3 g，線圈電阻為6 Ω，當彈簧剛度分別為1 N/mm、4 N/mm、7 N/mm時，出油口流量隨時間的變化特性如圖6 所示。閥口流量分別在第20.7 ms、第21.2 ms 和第22.5 ms 由0.79 L/min 降為0，電磁閥吸合時間分別為10.6 ms、11.1 ms 和12.4 ms。隨著彈簧剛度的增大，響應時間逐漸變長。

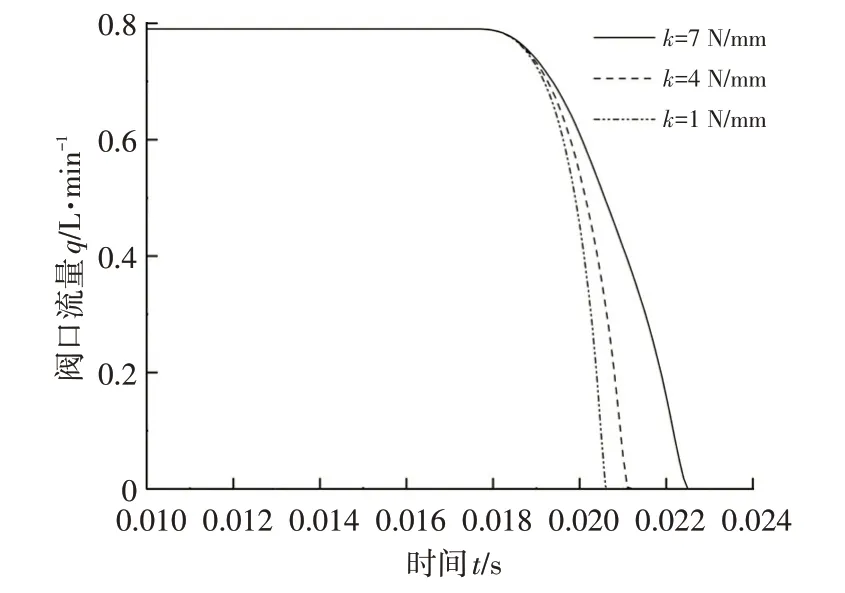
圖6 彈簧剛度對閥口流量的影響

設電磁閥進油口壓力為1 MPa，線圈電阻為6 Ω，彈簧剛度為1 N/mm，當閥芯動鐵質量分別為3.3 g、6.3 g、9.3 g 時，出油口流量隨時間的變化特性如圖7 所示。閥口流量分別在第20.7 ms、第21.5 ms 和第22.1 s 由0.79 L/min 降為0，電磁閥吸合時間分別為10.6 ms、11.4 ms和12.0 ms。電磁閥吸合時間隨閥芯動鐵總質量的增大而延長。

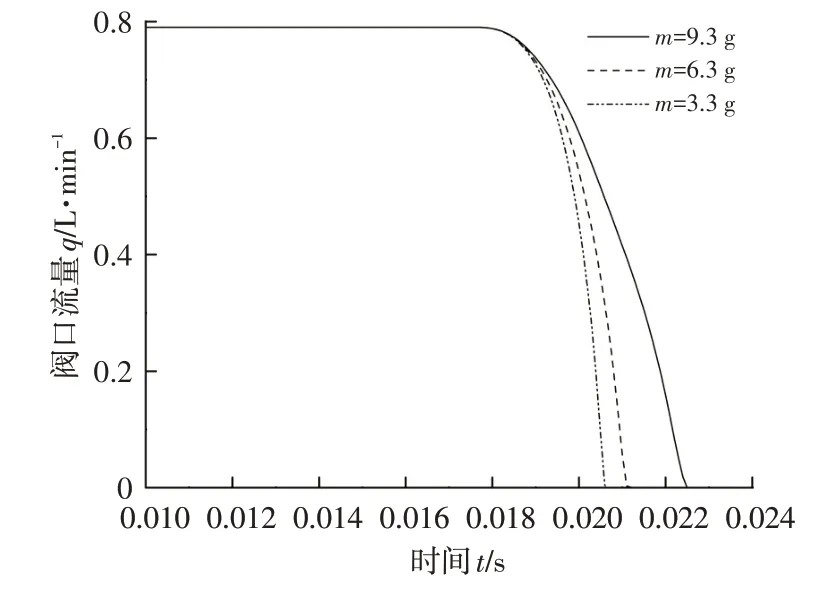
圖7 閥芯質量對閥口流量的影響

設電磁閥進油口壓力為1 MPa，閥芯動鐵總質量為3.3 g，彈簧剛度為1 N/mm，當線圈電阻分別為4 Ω、5 Ω、6 Ω 時，出油口流量隨時間的變化特性如圖8 所示。在第15.9 ms、第17.2 ms、第20.5 ms時電磁閥閥芯落座，閥口流量降為0，電磁閥吸合時間分別為5.8 ms、7.1 ms、10.4 ms。隨線圈電阻的增大，電磁閥吸合時間延長，響應速率變慢。

圖8 線圈電阻對閥口流量的影響

利用單一變量控制法對電磁閥吸合時間的影響因素分析可知，電磁閥吸合時間對線圈電阻的靈敏度較大。

5.DOE-GA算法優化設計

5.1 理論分析

試驗設計（Design of Experiment，DOE）是研究和處理多因子與響應變量關系的一種方法，通過建立響應與因子之間的函數關系，找出總體最優的改進方案，可用以下模型表征：

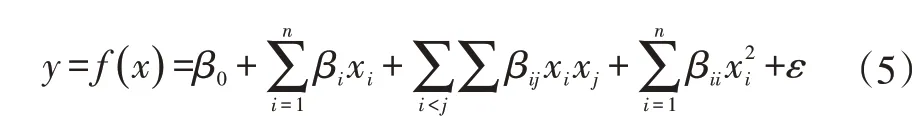
式中，為響應量；、β、β、β為系數；x、x為因子；(0,)為誤差。

遺傳算法（Genetic Algorithm，GA）以群體中的所有個體為對象，利用隨機化技術對一個被編碼的參數空間進行全局尋優，可簡化為：

式中，為基本空間。

電磁閥的吸合、釋放時間直接影響制動輪缸壓力的變化率。本文利用DOE-GA 算法將電磁閥動作時間從閥的特性指標中提取出并作為最小化目標參數。選擇彈簧剛度、線圈電阻、閥芯動鐵總質量為優化參數，設定閥芯吸合和釋放響應時間總和最短為優化目標。考慮到汽車實際工況和電磁閥特性，設定線圈電阻、閥芯總質量及彈簧剛度的約束區間為：

圖9 詳細闡述了優化過程，以電磁閥AMESim 模型為驗證平臺，通過DOE 獲取彈簧剛度、線圈電阻、閥芯動鐵總質量與閥芯吸合和釋放時間的響應曲面模型，利用遺傳算法對進行全局優化，尋找最佳個體，獲取最佳彈簧剛度、線圈電阻和閥芯總質量。

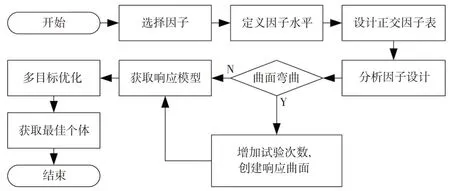
圖9 DOE優化流程

5.2 變量因子正交試驗規劃

變量因子取電磁閥彈簧剛度、線圈電阻及閥芯總質量，響應變量為電磁閥吸合時間及釋放時間。變量因子的限值如表3 所示，鑒于變量因子小于4 個，本文采用中心復合有界設計方法得到變量因子正交表，如表4所示。

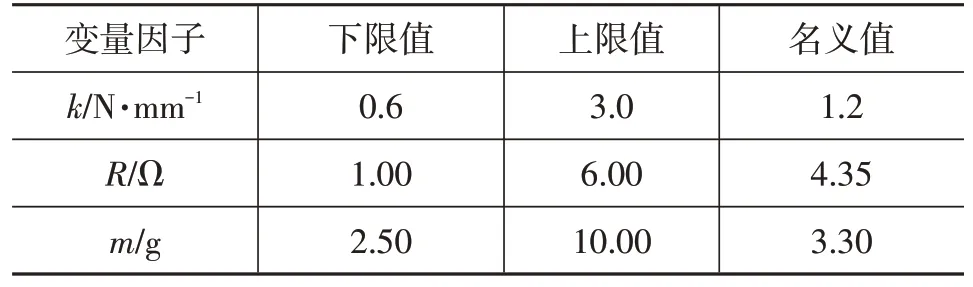
表3 變量因子兩水平限值

5.3 響應曲面擬合及效果評價

針對表4，基于電磁閥模型得到如圖10所示的試驗結果，采用最小二乘法建立電磁閥吸合時間、釋放時間與彈簧剛度、線圈電阻及閥芯動鐵質量間的二階響應曲面模型：

表4 三因子正交表

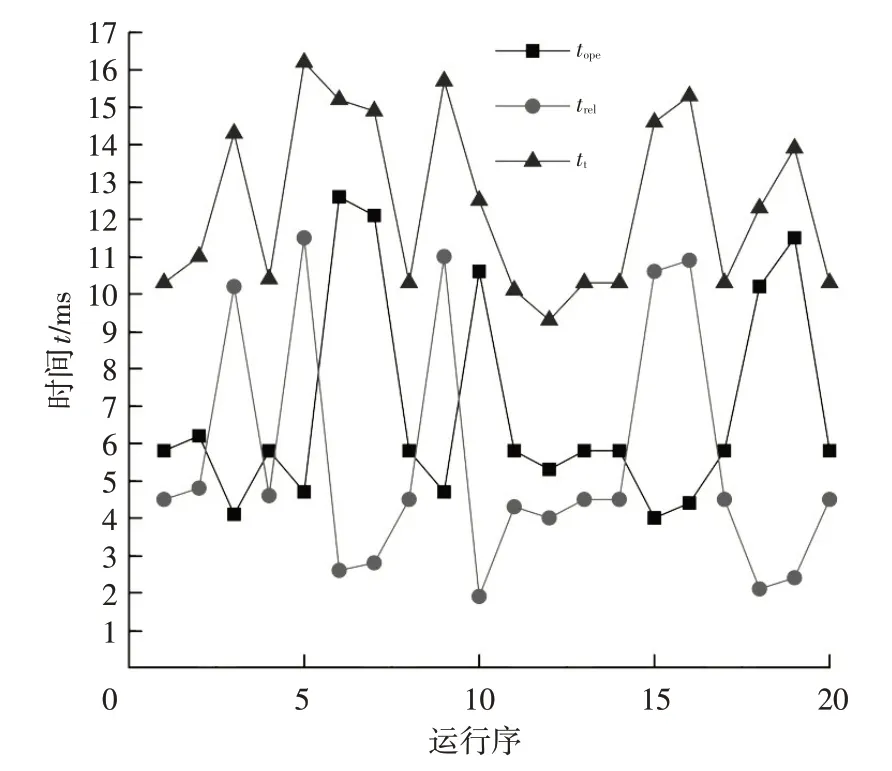
圖10 正交試驗結果

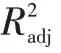
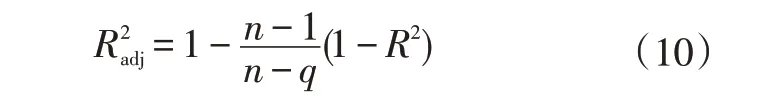
式中，為觀測值的總數量；為模型中的項數（包括常數項）；為變異系數。

文中響應變量、的修正決定系數分別為99.88%、97.49%，說明響應曲面=(,,)及=(,,)的擬合精度較高。

5.4 優化結果分析

5.4.1 構造目標函數

以電磁閥吸合及釋放的總響應時間最短構造目標函數，將電磁閥性能最優的實際問題轉化為求函數極小值的數學問題：

式中，λ(=1,2)為響應量的重要度，本文取λ=1，表征、的重要度相同。

5.4.2 全局尋優

本文采用遺傳算法對目標函數進行全局尋優，尋找最佳個體，獲取最優變量因子。算法的迭代過程如下：

a.對解的基本空間進行編碼。遺傳算法在進行搜索前先將表示成遺傳空間的基因型結構數據。

b.隨機初始化種群。本文設定初始種群規模為50，由遺傳算法通過初始種群生成函數隨機產生。

c.計算種群的適應度。依據目標函數編寫適應度函數，計算種群中個體的適應度，將適應度排序后編號。

d.生成子代。根據種群適應度均勻選擇父代，父本中5%的精英個體直接遺傳到下一代，雜交概率為80%。

e.適應度值評估檢測，選擇優良后代。計算交換產生的新個體的適應度，從交換后的群體中選出適應度好的個體，使它們有機會成為新的父代，繁衍下一代。

f.中止條件判定。依據設定的中止條件判定是否中止進化，若滿足中止條件（本文設定的適應度函數值的偏差為10），則退出進化輸出優化結果，否則跳轉至步驟d。

圖11 所示為電磁閥響應量遺傳算法優化曲線，代數-適應度曲線表征在迭代38次后優化算法收斂，閥芯吸合和釋放響應時間總和的最佳適應值為9.2 ms，此時變量因子彈簧剛度、線圈電阻及閥芯動鐵質量分別為0.6 N/mm、3.84 Ω、2.5 g。

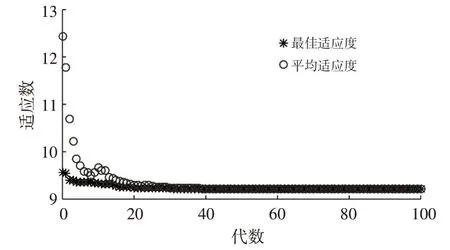
圖11 遺傳算法優化結果

為檢驗優化算法的有效性，本文將變量因子的優化值及名義值分別配置到模型中，電磁閥閥口流量響應時間如表5所示。

表5 優化前、后結果對比

由表5可知，優化后電磁閥吸合時間縮短14.1%，釋放時間縮短5.1%，有效地提高了電磁閥的動態響應特性。上述結果表明，DOE-GA算法處理多變量交互作用下電磁閥響應特性優化問題具有可行性。

6 結束語

本文以常開式電磁閥的AMESim模型為研究對象，通過開關電磁閥響應測試臺驗證了所建模型的有效性。基于試驗設計的建模方法，采用最小二乘法建立電磁閥吸合時間、釋放時間與變量因子的高精度響應曲面二階模型，利用遺傳算對電磁閥結構參數進行優化，優化后電磁閥吸合時間縮短14.1%，釋放時間縮短5.1%，有效地提高了電磁閥的動態響應特性。