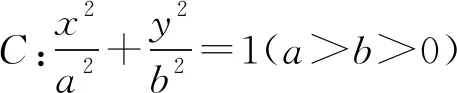2022年高考模擬試題(一)
胡貴平
(甘肅省白銀市第一中學 730900)
考生注意:
1.答卷前,考生務必將自己姓名、準考證號填寫在答題卡上.
2.回答選擇題時,選出每小題答案后,用2B鉛筆把答題卡上對應題目的答案標號框涂黑.如需改動,用橡皮擦干凈后,再選涂其它答案標號框.回答非選擇題時,將答案寫在答題卡上.寫在本試卷上無效.
3.考試結束后,將本試卷和答題卡一并交回.
一、選擇題(本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的.)
1.已知集合A={x|0 A.{x|x>0} B.{x|1≤x<4} C.{x|x≥1} D.{x|x<4} 解析依題意A∪B={x|x>0}.故選A. 3.在一個文藝比賽中,12名專業人士和12名觀眾代表各組成一個評判小組,給參賽選手打分.根據兩個評判小組對同一名選手的打分繪制了如圖1的折線圖. 圖1 根據以上折線圖,下列結論錯誤的是( ). A.A小組打分分值的最高分為55分,最低分為42分 B.A小組打分分值的標準差小于B小組打分分值的標準差 C.B小組打分分值的中位數為56.5 D.B小組更像是由專業人士組成的 故選C. A.3 B.6 C.9 D.12 圖2 故z=3x+y的最大值是3×4-3=9,故選C. 8.已知兩條不同的直線l,m和不重合的兩個平面α,β,且l⊥β,有下面四個命題:①若m⊥β,則l∥m;②若α∥β,則l⊥a;③若α⊥β,則l∥α;④若l⊥m,則m∥β.其中真命題的序號是( ). A.①② B.②③ C.②③④ D.①④ 解析因為兩條不同的直線l,m和不重合的兩個平面α,β,且l⊥β, 對于①,由l⊥β,m⊥β,可得l∥m,故①正確; 對于②,若l⊥β,α∥β,可得l⊥α,故②正確; 對于③,若l⊥β,α⊥β,則有可能l?α,故③錯誤; 對于④,當l⊥β,l⊥m時,則有可能m?β,故④錯誤. 綜上,真命題的序號是①②.故選A. 圖3 10.在△ABC中,角A,B,C的對邊分別是a,b,c,且A,B,C成等差數列,a+c=2,則b的取值范圍是( ). 由余弦定理b2=a2+c2-2accosB,可得 所以1≤4-3ac<4.即1≤b2<4,解得1≤b<2.所以b的取值范圍是[1,2).故選A. 圖4 解析如圖5,延長AB至點E,使AB=BE,連接SE,CE,OC. 圖5 因為D是母線SA的中點,所以SE∥BD. 所以∠CSE為異面直線SC與BD所成的角(或補角). 由題意知OE=6,OC=2. 所以在Rt△COE中, 在△SCE中,SC=4,則由余弦定理,得 故選A. A.b>a>cB.a>c>bC.c>a>bD.b>c>a 圖6 圖7 ① 又-lnx1>lnx2,故lnx1x2<0,即x1x2<1. ② (一)必考題:共60分. ① ② 由① - ②,得 18.2020年5月28日,十三屆全國人大三次會議表決通過了《中華人民共和國民法典》,自2021年1月1日起施行.《中華人民共和國民法典》被稱為“社會生活的百科全書”,是新中國第一部以法典命名的法律,在法律體系中居于基礎性地位,也是市場經濟的基本法,為了增強學生的法律意識,了解法律知識,某校組織全校學生進行學習《中華人民共和國民法典》知識競賽,從中隨機抽取100名學生的成績(單位:分)統計得到如下表格: 0,60 60,70 70,80 80,90 90,100 男51416134女31113156 規定成績在[90,100]內的學生獲優秀獎. (1)根據以上成績統計,判斷是否有90%的把握認為該校學生在知識競賽中獲優秀獎與性別有關? (2)在抽取的100名學生中,若從獲優秀獎的學生中隨機抽取3人進行座談,記X為抽到獲優秀獎的女生人數,求X的分布列和數學期望. 附: PK2≥k 0.10.010.001k2.7066.63510.828 解析(1)依題意得,列聯表如下: 是否獲獎性別 獲優秀獎未獲優秀獎合計男44852女64248合計1090100 假設H0:“該校學生在知識競賽中獲優秀獎與性別無關”. 當H0成立時,P(K2≥2.706)≈0.1. 將列聯表中的數據代入公式,計算得 因為0.641<2.706,所以小概率事件未發生.從而接受假設H0. 所以在犯錯誤的概率不超過0.1的前提下可以推斷該校學生在知識競賽中獲優秀獎與性別無關,即有90%的把握認為該校學生在知識競賽中獲優秀獎與性別無關. (2)依題意得,X的所有可能取值為0,1,2,3, 所以X的分布列為 X0123P1303101216 19.(12分)如圖8,三棱柱ABC-A1B1C1中,∠A1AC=60°,AC⊥BC,A1C⊥AB,AC=1,AA1=2. 圖8 (1)求證:A1C⊥平面ABC; 解析(1)在△A1AC中,∠A1AC=60°,AC=1,AA1=2. 又因為A1C⊥AB,AB∩AC=A, 所以A1C⊥平面ABC. (2)由(1)知:CA,CB,CA1兩兩垂直. 圖9 解得b=1,可得點B(0,1,0). (1)求橢圓C的方程; (2)設橢圓C上存在兩點M,N,使得PM的斜率與PN的斜率之和為-1,直線MN是否過定點,若是,求出定點的坐標,若不是,說明理由. 解得a2=16,b2=12. (2)當直線MN的斜率存在時,設方程為y=kx+m.代入橢圓方程消去y并整理,得 (3+4k2)x2+8kmx+4m2-48=0. 設點M(x1,y1),N(x2,y2),則 ① 所以(2k+1)x1x2+(m-2k-5)(x1+x2)+16-4m=0. 將①代入, 整理化簡,得 16k2+10km-24k+m2-3m=0. 即(2k+m-3)(8k+m)=0. 因為P(2,3)不在直線MN上, 所以2k+m-3≠0. 所以m=-8k. 于是MN的方程為y=k(x-8). 所以直線過定點(8,0). 當直線MN的斜率不存在時,可得N(x1,-y1),不符合題意. 綜上所述,直線MN過定點(8,0). (1)當a=0時,求函數f(x)的單調性和極值; 由f′(x)=0得x=e.由f′(x)>0得x>e,f′(x)<0得0 x0,e ee,+∞ f 'x -0+fx ↘極小值↗ 所以f(x)在(0,e)上單調遞減,在(e,+∞)上單調遞增. xex-lnx-x-1≥0. 設g(x)=xex-lnx-x-1, 故g′(x)單調遞增. 當x∈(0,x0)時,g′(x)<0,函數g(x)單調遞減; 當x∈(x0,+∞)時,g′(x)>0,函數g(x)單調遞增. 所以當x=x0時,g(x)取得最小值. (二)選考題(共10分.請考生在第22,23題中選定一題作答,并用2B鉛筆在答題卡上將所選題目對應的題號方框涂黑.按所涂題號進行評分,不涂、多涂均按所答第一題評分;多答按所答第一題評分.) (1)求C1,C2的極坐標方程; 解析(1)因為x=ρcosθ,y=ρsinθ, 因為x=ρcosθ,y=ρsinθ, 所以(ρcosθ)2+(ρsinθ-1)2=1. 所以ρ2-2ρsinθ=0.所以C2:ρ=2sinθ. 23.[選修4-5:不等式選講](10分) 已知函數f(x)=|2x+a|,g(x)=|x-b|. (1)若a=1,b=3,解不等式f(x)+g(x)≥4; 當x>3時,由3x-2≥4,解得x>3. (2)當a>0,b>0時,由不等式的性質,得 f(x)-2g(x)=|2x+a|-2|x-b|=|2x+a|-|2x-2b|≤|2x+a-2x+2b|=a+2b. 所以a+2b=3.
















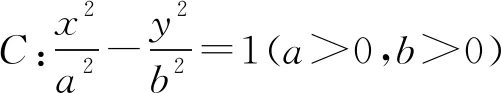

















二、填空題(本大題共4小題,每小題5分,共20分).











三、解答題(共70分.解答應寫出文字說明、證明過程或演算步驟.第17~21題為必考題,每個試題考生都必須作答.第22,23題為選考題,考生根據要求作答.)