基于流量校準的吸附測量方法及誤差分析

劉碧強，曹海山

（清華大學機械工程學院能源與動力工程系，北京 100084）

引 言

固氣界面上的吸附現象是指當氣體分子運動到固體表面時，由于氣體分子與固體分子之間的相互作用，氣體分子會停留在固體表面，從而使固體表面的氣體分子濃度增大。隨著生產水平和科學研究的不斷發展，固氣界面的吸附作用已廣泛應用于混合物分離提純[1?2]、氣體存儲[3?5]、污水處理[6]和工業催化[7]等領域。

在吸附研究中，吸附量是最重要的物理量。在恒定溫度下，氣體吸附量和固氣吸附平衡壓力之間的關系曲線稱為吸附等溫線。根據吸附等溫線的形狀和變化規律可以了解吸附質和吸附劑的作用強弱、界面上吸附分子的狀態、吸附層結構等信息[8]。

常用的吸附測量方法有容積法[9?13]和質量法[14?16]。容積法出現時間最早[17]，技術成熟，目前已作為標準被廣泛采用[18]。其原理是基于被校準過的體積和壓力、溫度測量值，結合氣體狀態方程可計算得到吸附前后系統內自由狀態氣體量，吸附前后系統內氣體量差值即為樣品吸附量。容積法吸附測量系統簡單，易實現自動化控制；但平衡時間長，測量精度易受氣體狀態方程選取、儀表精度、容積標定精度[19]、氣體管路溫度均勻性等影響。質量法是通過測量吸附前后的樣品質量直接得到吸附量。根據采用的稱重天平種類可分為石英彈簧法[20]、電子天平法[21]、磁懸浮法[22]。相比于容積法，質量法無須校正死體積，測量精度主要受限于氣體浮力、溫差和天平精度的影響，測量誤差相對容易控制[23]。

傳統容積法吸附測量方法中，測量結果的可靠性受到氣體分配管路溫度均勻性的嚴重影響，且缺少校準系統。針對上述問題，本文提出了一種改進的容積法吸附測量方法，在樣品室入口前布置質量流量控制器，根據質量流量測量結果對吸附測量值進行校準，且由于質量流量測量不受溫度影響，因此在氣體管路溫度均勻性難以保證的情況下可提升測量結構的精度。本文詳細分析了吸附測量過程中的誤差傳遞，從結構參數、物性參數和儀表精度三個方面對比了傳統容積法和基于流量校準的容積法。研究結果對于提升容積法吸附測量精度具有重要意義。

1 一種質量流量控制器校準的容積法吸附測量方法

傳統容積法是根據質量守恒定律和氣體狀態方程得到吸附前后平衡態的參數關系，吸附前后自由態氣體分子的減少量等于吸附的氣體分子量。其一般關系式可表示為

式中，下角標1、2分別表示系統的兩個平衡態；p是壓力；V是容積；T是溫度；R是氣體常數；Z是氣體在壓力p和溫度T下的壓縮因子；nads是系統的氣體吸附量。

傳統容積法吸附測量部件包括氣體分配系統、校準腔、樣品室，如圖1所示。其中氣體分配系統與真空系統、工質氣瓶、校準腔和樣品室連接，控制氣體的進出；校準腔與氣體分配系統放置在恒溫箱中。吸附測量系統的各平衡狀態如表1 所示，根據平衡態1～3 可得到氣體分配系統和校準腔的容積，再結合平衡態4 得到加入樣品后的樣品室容積，結合平衡態5得到測量溫度下的樣品室等效平均溫度Teff。基于已得到的腔體容積，結合平衡態6～7 可計算得到樣品比吸附量。

圖1 容積法吸附測量裝置原理圖Fig.1 The schematic diagram of volumetric adsorption measurement instrument

通過一般關系式(1)和表1可依次計算得到氣體分配系統容積VM、加入樣品后的樣品室容積VS、樣品室等效平均溫度Teff和樣品比吸附量xads的表達式。

表1 吸附測量系統的各平衡狀態Table 1 Various equilibrium states of the adsorption measurement system

式中，下角標V 表示基于傳統容積法的測量參數；Vcal是校準球體積；Z1、Z2、Z3、Z4、Z5分別是氦氣在壓力p1、p2、p3、p4、p5和溫度T1下的壓縮因子；Zeff是氦氣在壓力p5和溫度Teff下的壓縮因子；Z6、Z7分別是吸附氣體在壓力p6、p7和溫度T1下的壓縮因子;Zeff,ads是吸附氣體在壓力p8和溫度Teff下的壓縮因子;Mads是吸附氣體的摩爾質量；msample是樣品質量。

本文提出的吸附測量方法在傳統的容積法基礎上將樣品室入口的閥門改為質量流量控制器。該方法通過質量流量控制器測量流經的氣體量，測量精度不受溫度影響，且結合質量守恒定律和氣體狀態方程對測量結果進行計算校準，提升測量可靠性。

以氣體分配系統容積為例，質量流量控制器將樣品室和氣體分配系統分隔開，當流量控制器閥門打開時，由質量守恒方程有：

式中，mVM,He是在測量氣體分配系統容積過程中流量控制器測量得到的流經氦氣質量，有正負號之分，“+”表示流出氣體分配系統，“?”表示流入氣體分配系統；MHe是氦氣的摩爾質量；下角標m 表示基于質量流量測量值的測量參數。

由式(6)可得到氣體分配系統容積的表達式：

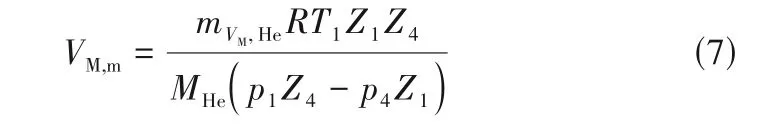
如圖2 所示，可依次得到加入樣品后的樣品室容積VS、等效平均溫度Teff和樣品比吸附量xads的表達式：

圖2 基于流量校準的吸附測量流程圖Fig.2 Flowchart of the adsorption measurement based on flow calibration

式中，mT,He，mads分別是等效平均溫度和吸附量測定過程中流經質量流量控制器的氣體質量。

對比式(5)和式(10)可看出，傳統容積法測量結果易受氣體分配系統溫度影響，而基于流量校準的容積法測量結果與氣體分配系統溫度無關，因此加入質量流量控制器可提升在溫度分布均勻性較差時的測量精度，拓展應用范圍。

2 誤差分析

本節以不確定度作為評價參數，針對結構參數、物性參數和儀表精度對測量結果的影響進行討論。圖3給出了傳統容積法和基于流量校準的容積法中測量結果的影響因素。

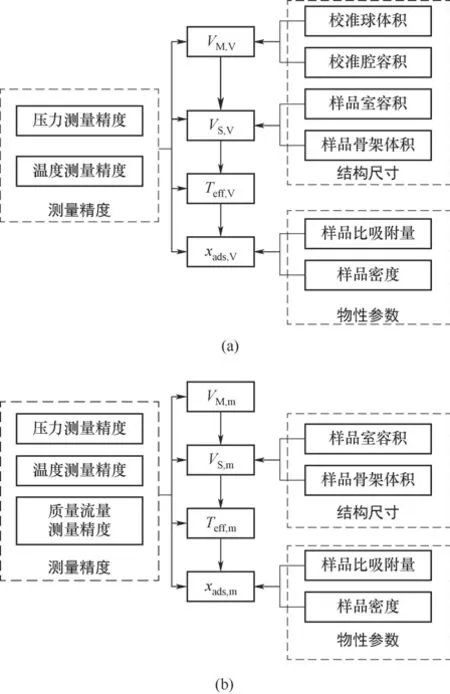
圖3 各因素影響(a)容積法;(b)基于流量校準的吸附測量Fig.3 Influence of various factors in volumetric adsorption measurement(a)and adsorption measurement based on flow calibration(b)

2.1 測量不確定度

測量標準不確定度的一般表達式為

式中，ur,A是A的相對不確定度；是A的測量平均值。

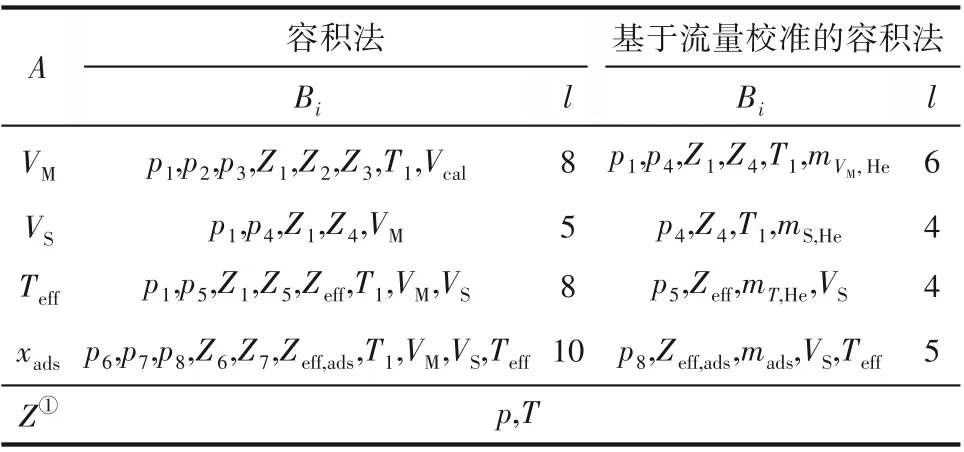
表2 兩種方法測量不確定度表達式參數Table 2 Parameters of measurement uncertainty expression in both methods

2.2 參數設置

初始參數設定如表3 所示，其中為保證低壓下的測量精度，采用0～6 bar、0～200 bar（1 bar=105Pa）兩個不同量程的壓力表進行測量。溫度測量誤差限計算公式為式(13)。假設溫度、壓力和質量流量的測量值在測量誤差限內服從均勻分布，根據標準不確定度的B類評定法，可通過式(15)計算得到標準不確定度。基于上述參數，開展后續參數影響分析。

表3 基本參數設定Table 3 Basic parameter set

式中，t是溫度,℃；R(t)是溫度傳感器電阻與溫度的關系式；R'(t)是R(t)關于t的導數。

式中，R0是0℃時溫度傳感器阻值，1 kΩ；a，b，c為系數，分別為3.9083 × 10?3℃?1、?5.775 × 10?7℃?2和?4.183 × 10?12℃?4。

式中，σ是誤差限。

2.3 結構參數影響

結構參數包括Vcal、校準腔容積VC、樣品室總容積VStotal和樣品骨架體積Vsample。

2.3.1 校準球體積 以Vcal與VC的比值rVcal作為衡量參數，VM的相對不確定度ur,VM隨rVcal和p1的變化規律如圖4 所示。假設校準球體積的誤差限σcal與rVcal的關系如式(16)所示。從圖4 可知，不同rVcal對應的ur,VM隨初始壓力p1的變化規律一致，在1～6 bar 和10～100 bar 區間內ur,VM隨p1逐漸減小，在6～10 bar 區間內ur,VM激增的原因是壓力測量儀器量程從低量程切換到高量程，壓力測量誤差發生變化。圖5 展示了ur,VM極小值隨rVcal的變化情況，可看出隨著rVcal增大，ur,VM極小值下降，且下降趨勢變緩。綜合考慮誤差和系統尺寸，rVcal取值60%。

圖4 氣體分配系統容積相對不確定度與校準球體積的關系Fig.4 Relationship between relative uncertainty of manifold volume and calibration ball volume

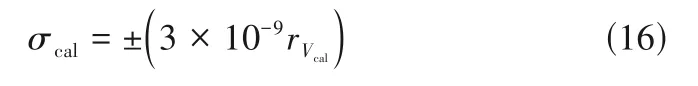
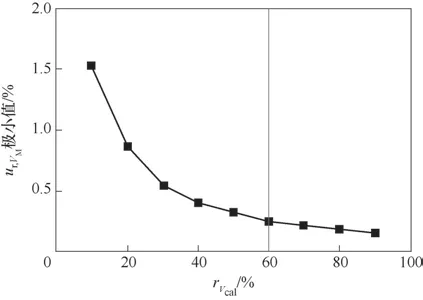
圖5 氣體分配系統容積相對不確定度極小值與校準球體積的關系Fig.5 Relationship between minimum relative uncertainty of manifold volume and calibration ball volume

2.3.2 校準腔容積 以VC與VM的比值rVC作為衡量參數，基于2.3.1 節的分析結果，圖6 給出了不同rVC下ur,VM隨p1的變化情況。從圖6可看出，各曲線變化規律保持一致，區別在于隨著rVC的增大，變化曲線從單峰變為雙峰，最后穩定為三峰，這是測量時初始壓力p1和平衡壓力p2,p3之間的差距導致的。當rVC小時，p1,p2,p3三者測量值相近，在p1從6 bar 變為7 bar 時，三者均超出低壓壓力表量程，因此出現單一峰。隨著rVC增大，p1,p2,p3之間的差異增大，出現p1或p3處于高壓力量程而p2處于低壓力量程的情況，從而導致多峰。圖7 給出了ur,VM極小值隨rVC的變化情況，從圖中可看出，ur,VM極小值隨rVC先減后增，這是校準球體積增大和平衡壓力差值增大帶來的綜合影響。VC增大會提高系統溫度均勻分布的控制難度，綜合考慮控制難度和測量精度，rVC取80%。

2.3.3 樣品室容積 以VStotal與VM的比值rVStotal作為衡量參數，在2.3.1 節和2.3.2 節的分析基礎上，圖8對比了兩種方法測量的樣品室容積不確定度隨p1和rVStotal的變化情況，其中樣品體積取樣品室容積的30%。兩種方法的樣品室容積不確定度隨壓力變化情況相同，區別在于容積法會出現雙峰，原因與2.3.1 節相同，基于流量校準的容積法為單峰，原因是計算過程中壓力相關項為一個。然而，兩者隨樣品室容積的變化趨勢相反，這是因為在流量校準的容積法中，樣品室體積增大使得達到同一壓力狀態所需流入樣品室的氣體質量增大，對應的不確定度因子增大，最終體現出正相關的趨勢。圖9給出了兩種方法測量的樣品室容積不確定度極小值隨樣品室容積的變化規律。從圖中可看出，容積法極小值變化明顯，基于流量校準的容積法極小值變化很小。因此在容積法吸附測量中，綜合考慮尺寸和精度需求，rVStotal取100%；在基于流量校準的吸附測量中，樣品室容積的取值可優先考慮如空間布局等其他因素的影響。

圖8 樣品室容積相對不確定度與樣品室容積的關系Fig.8 Relationship between relative uncertainty of sample chamber volume and sample chamber volume

圖9 樣品室容積相對不確定度極小值與樣品室容積的關系Fig.9 Relationship between minimum relative uncertainty of sample chamber volume and its value

2.3.4 樣品骨架體積 假設樣品比吸附量為0.067 g/g，以Vsample與VStotal的比值rVsample作為衡量參數，在2.3.1～2.3.3 節的分析基礎上，圖10 給出了兩種方法測量不確定度ur,xads隨p8和rVsample的變化情況。從圖10 中可看出，兩種方法的比吸附量不確定度均與測量壓力p8正相關，與rVsample負相關。綜合考慮實際填充率和測量精度，取樣品骨架體積占比為40%。

圖10 比過剩吸附量相對不確定度與樣品骨架體積占比的關系Fig.10 Relationship between relative uncertainty of excess adsorption amount and sample skeleton volume

2.4 樣品物性影響

樣品物性包括比過剩吸附量xads和樣品密度ρads。在2.3 節分析結果基礎上，圖11 對比了容積法和基于流量校準的容積法測量結果不確定度隨比過剩吸附量xads和樣品密度ρads的變化情況。從圖中可看出，兩種測量方法變化規律保持一致，區別在于容積法測量不確定度數值和隨比過剩吸附量、樣品密度的變化程度更大，這是因為容積法計算過程中與壓力相關的不確定度因子數量更多。

圖11 比過剩吸附量相對不確定度和比過剩吸附量(a)、樣品密度(b)的關系Fig.11 Relationship between relative uncertainty of excess adsorption amount and excess adsorption amount(a),sample density(b)

2.5 儀表精度影響

儀表精度包括壓力、溫度和質量流量的測量精度。圖12 對比了兩種方法相對不確定度隨壓力測量精度、溫度測量精度的變化情況。從圖中可看出，兩種方法測量不確定度隨壓力測量精度和溫度測量精度變化規律一致，區別在于容積法數值和變化趨勢更大，這是因為容積法計算過程中與壓力測量精度和溫度測量精度相關的不確定度因子數量更多。

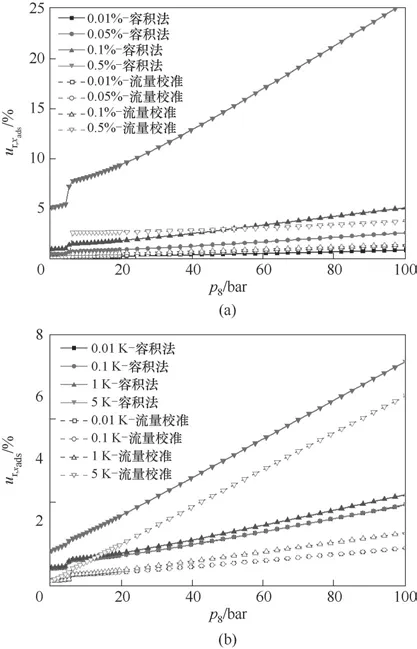
圖12 比過剩吸附量相對不確定度與壓力測量精度(a)、溫度測量精度(b)的關系Fig.12 Relationship between relative uncertainty of excess adsorption amount and pressure measurement accuracy(a),temperature measurement accuracy(b)

圖13 展示了基于流量校準的吸附測量不確定度隨質量流量測量精度的變化情況。從圖中可看出，測量不確定度隨質量流量測量精度降低而增大，這是因為精度降低造成流經質量流量控制器的氣體質量不確定度因子增大。

圖13 比過剩吸附量相對不確定度與質量流量測量精度的關系Fig.13 Relationship between relative uncertainty of excess adsorption amount and mass flow measurement accuracy

3 結 論

本文在容積法吸附測量中加入質量流量控制器，用以提升溫度均勻性難以保證時的測量精度，并提高測量結果的可靠性。本文分析了兩種測量方法的誤差傳遞過程，并對比了結構參數、物性參數和儀表精度對測量結果的影響。基于分析結果可得到以下結論。

（1）相比傳統容積法，基于流量校準的吸附測量方法誤差因子數量更少，可實現更低的測量誤差。

（2）增大樣品量、比過剩吸附量、密度和儀表精度可提升兩種方法的測量精度，增大校準球體積可提升傳統容積法的測量精度。

（3）校準腔容積存在最優值，使得氣體分配系統容積標定誤差最小；質量流量測量誤差的引入增大了容積變化對樣品室容積不確定度的影響，造成樣品室容積對兩種方法測量結果的影響規律不同。

上述結論是基于所研究的結構參數和測量條件得到的，其普適性有待進一步研究。影響吸附測量精度的直接原因是平衡態直接測量誤差項(p,T,m)的變化，結構參數、物性參數的變化改變了其誤差傳遞系數，儀表精度的變化改變了其測量不確定度。本文研究狀態離實際應用還存在一定差距，如溫度波動對壓力傳感器測量精度的影響以及氣體分配系統溫度均勻性的影響還需要進行考慮。此外，實際應用中應權衡測量精度、空間布置方式和重復實驗需求，對吸附測量系統進行合理布置。今后工作將對溫度波動和溫度均勻性進行分析，并結合實驗開展研究，以求獲取具有明確普適性的影響規律，對實際系統設計進行指導。

符 號 說 明

M——摩爾質量，kg/mol

m——氣體質量，kg

n——物質的量，mol

Zeff——氦氣在壓力p5，溫度Teff下的壓縮因子

Zeff,ads——吸附氣體在壓力p8，溫度Teff下的壓縮因子

下角標

ads——吸附氣體

C——校準腔

cal——校準球

eff——等效平均值

He——氦氣

M——氣體分配系統

m——基于流量校準的吸附測量

S——加入樣品后的樣品室

Stotal——未加入樣品的樣品室

sample——樣品