方形微通道內超臨界CO2流動換熱特性研究

許婉婷，許波，王鑫，陳振乾

（東南大學能源與環境學院，江蘇南京 210096）

引 言

在當前“雙碳”目標的政策背景以及熱工設備小型化的行業趨勢下，超臨界二氧化碳因其獨特的物性優勢在核反應堆、太陽能熱發電系統、新型制冷與空調系統、火箭推動器的熱保護等領域備受青睞，以超臨界CO2為傳熱流體的微通道換熱器將成為下一代高效能源系統的重要組成部分[1?4]。二氧化碳的臨界點較低（Pc= 7.38 MPa，Tc= 304.13 K），其超臨界狀態較易獲得，使用CO2作為換熱工質的動力轉換系統在較低的工作溫度和壓力下便可以獲得較高的系統效率[5]。然而，如圖1 所示，超臨界CO2在擬臨界溫度附近，其熱物性參數（密度、比熱容、黏度和熱導率等）變化劇烈，傳統的常物性流動換熱規律和經驗公式不再適用。因此，全面了解超臨界CO2在管內的流動換熱特性對微通道換熱器的設計和優化具有重要意義。

自20 世紀50 年代以來，國內外學者對超臨界CO2的換熱特性進行了大量的實驗和數值模擬研究，但是主要針對豎直圓管內的向上和向下流動[6?9]。事實上，非豎直方向流動時，重力與流體流動方向并不平行，超臨界CO2在管內流動時更易受到浮升力的影響，換熱規律更加復雜。Liao 等[10]實驗研究發現超臨界CO2在水平微型圓管內流動時，在部分工況下會出現局部換熱惡化，而在向上和向下流動時均在一定程度上強化了換熱。Kim 等[11]進行了超臨界CO2在內徑為7.5 mm水平管內對流換熱的實驗研究，結果表明，由于浮升力的作用，壁溫呈現出非均勻分布的特點。Wang 等[12]數值模擬了直徑為22.14 mm的水平圓管內超臨界CO2的流動換熱特性，發現浮升力主要通過誘導二次流影響流動結構和湍流水平。Kumar 等[13]采用參數化模擬方法研究了超臨界CO2在內徑為2 mm 水平圓管內的熱工性能，指出熱通量對換熱惡化有顯著影響，較高的熱通量會導致傳熱系數峰值的降低。關于熱通量對傳熱系數的影響，也有學者提出了不同的見解。Xiang 等[14]對超臨界CO2在冷卻條件下的水平管內對流換熱進行了數值研究，指出熱通量對傳熱系數峰值數值影響不明顯，但對峰值出現的位置影響較大。楊傳勇等[15]模擬分析了超臨界CO2在內徑為0.5 mm、傾斜向上30°的圓管內的對流換熱過程，結果表明上母線壁溫高于下母線，相比于質量流量，熱通量對上母線處的傳熱系數、相對二次流動能影響較小。閆晨帥等[16]對超臨界CO2在內徑為10 mm、傾斜角度為45°的加熱圓管內的換熱行為進行數值模擬，指出類氣膜厚度、湍動能和軸向速度是造成頂母線壁溫分布出現差異的主要因素。

上述研究絕大多數是在圓形直管中進行的，實際上，管型的不同往往會影響流體的流動換熱特性。由于半圓形通道和方形通道在印刷電路板式換熱器中表現出的結構緊湊、密閉性好、金屬材料耗材少的特點，應用前景廣闊，已有研究者對方管[17?18]、半圓管[19?21]中的超臨界CO2換熱特性進行了研究。此外，凹管[22]、螺旋管[23]、U 型管[24]等強化管道也引起了學者的極大興趣。Kim 等[25]實驗研究了圓形、三角形和正方形通道壁面溫度的變化規律，對于非圓形通道，在相同的工況條件下，壁面溫度峰值比圓形通道出現得早。Hasan 等[26]數值模擬分析了不同截面（方形、矩形、等三角形和梯形）通道形狀對相同體積換熱器性能的影響，結果表明，方形通道的綜合性能優于其他三種通道。Besarati 等[27]建立了超臨界CO2在方形通道內從530℃被加熱到700℃時的傳熱模型和壓降模型，通過數值計算得出結論，方形通道的水力直徑越大，熱性能越差，質量流率的增加有利于換熱。Zhang 等[28]對超臨界CO2在水力直徑為1.16 mm 的圓管、半圓形管、方形管三種管型中的熱力學特性進行了數值研究，結果表明用半圓管和方管代替圓管可以減弱加熱條件下入口效應和浮升力效應造成的局部換熱惡化現象。Lei 等[29]數值研究了水平方形波狀微通道內超臨界CO2的冷卻換熱行為，結果表明，在一定程度上增大振幅或者減小波長，有利于提高綜合換熱性能。Khalesi 等[30]對超臨界CO2和液體鈉在方形微通道內的層流和耦合傳熱進行了數值分析，在臨界區和擬臨界區，超臨界CO2性質的劇烈變化會影響流動和傳熱，操作條件越遠離臨界點，這種影響就越小。

目前超臨界CO2在大直徑圓管內的流動換熱研究較為廣泛，關于非圓形微通道內流動換熱行為的研究較少，尤其是傾斜角度對其的影響更少有涉及。本文在驗證SSTk?ω湍流模型準確性的基礎上，對比分析超臨界CO2在方形微通道和半圓形微通道內水平流動的換熱性能差異，以方形微通道為研究重點，通過對比三種壁面平均傳熱系數探究常重力條件下熱通量、質量流量和傾斜角度對換熱性能的影響，并從沿程浮升力參數和二次流強度的角度分析運行參數影響換熱水平的原因，為后續方形微通道管內流動的強化換熱奠定基礎。

1 數值模型

1.1 物理模型與邊界條件

方形微通道和半圓形微通道的物理模型如圖2所示，管道截面的水力直徑均為Dh= 0.9 mm，管道總長均為1000 mm。為避免入口端的入口效應及出口端的回流效應，在加熱段兩端各設置長度為200 mm 的絕熱段，管道的有效加熱長度為600 mm。建立物理模型時，z軸正方向始終為流體的流動方向，流體流動方向與水平面的夾角為α，定義α=0°為水平方向流動，α=90°為豎直向上流動，α=?90°為豎直向下流動。將方管類比圓管，沿流動方向的截面上周向角度為θ，從y軸正半軸順時針旋轉，定義其范圍為θ∈[0°～360°]。

為研究超臨界CO2在近臨界點區域于方形微通道的流動換熱特性，本文探討了8.0 MPa 壓力下，質量流量G、熱通量q及傾斜角度α對流動換熱特性的影響，邊界條件設置如表1。

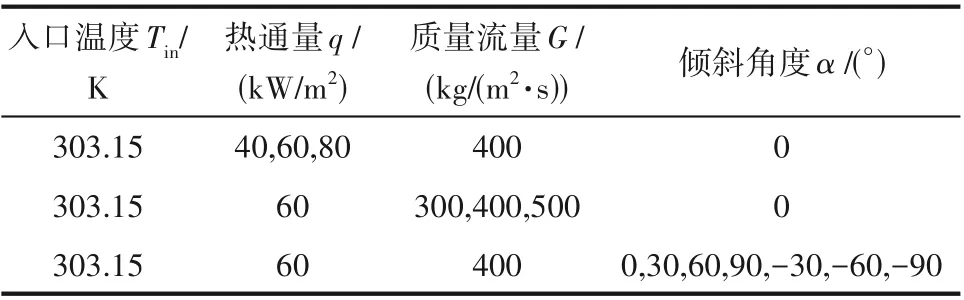
表1 不同模擬工況的邊界條件設置Table 1 Boundary conditions under different simulated conditions

1.2 模型假設與計算方法

為簡化模型，做出如下假設：

（1）流體在管內為穩態流動，無內熱源；

（2）壁面熱通量是均勻的；

（3）忽略流體流動時外壁與環境之間的熱交換；

（4）忽略管道壁厚。

采用CFD 模擬軟件數值求解連續性方程、能量方程、動量方程得到超臨界CO2在管內的流動換熱過程，其表達式分別如下：

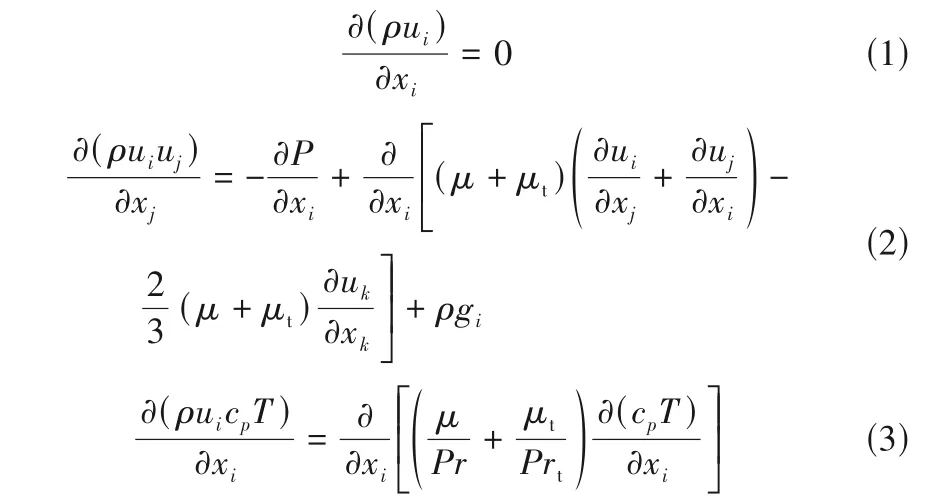
式中，ρ為密度；μ為動力黏度；μt為湍流動力黏度；Pr為Prandtl數；Prt為湍流Prandtl數。

由于超臨界CO2在擬臨界溫度附近熱物性參數變化的劇烈性，選取合適的湍流模型以準確捕捉其在流動過程中各項物性的變化是數值模擬的難點之一。根據已有文獻，數值模擬分析超臨界CO2管內流動特性時，多數均選取低Reynolds數湍流模型，已有多位學者證實SSTk?ω模型在超臨界流體流動換熱模擬的優越性[9,14,20,31]。SSTk?ω模型融合了k?ε模型對充分發展主流區域湍流計算的魯棒性和k?ω模型對近壁面區域流體流動特性的細致捕捉，能夠有效地體現出浮升力效應的影響，其輸運方程如下[32]：

式中，Γk和Γω分別表示k和ω的有效擴散系數;Gk和Gω分別表示k和ω的產生項；Yk和Yω分別表示由于湍流產生的k和ω的耗散項；Sk和Sω分別表示k和ω的自定義源項；Dω表示交叉擴散項。

流體入口設置為質量流量入口，出口為壓力出口邊界，入口絕熱段和出口絕熱段設置為絕熱壁面邊界，有效加熱段設置為恒熱流壁面。采用有限體積法離散各項控制方程，壓力?速度耦合方程采用SIMPLEC 算法求解，動量方程、能量方程等均采用二階迎風格式，亞松弛因子保持默認值不變。計算時直接調用Fluent中的nist?real?gas?model 模型，以準確反映流動換熱過程的物性變化。當各項殘差值均小于10?6，且出口溫度的監測值保持不變時，可認為計算收斂。

1.3 網格劃分及獨立性檢驗

流體流動全域采用結構性網格的劃分方式，由于SSTk?ω湍流模型對近壁面處的網格質量要求較高，網格劃分時，加密處理近壁面處的網格，合理設置第一層網格高度，保證無量綱壁面距離y+小于1。核算驗證模擬結果，y+均小于1，表明采用該網格可捕捉到近壁面處的流體流動特性。

為均衡網格數量和模擬精度之間的矛盾性，兩種模型分別選擇6 種不同數量的網格進行獨立性檢驗。邊界條件設置為：壓力P= 8.0 MPa，入口溫度Tin= 303.15 K，質量流量G= 400 kg/(m2·s)，熱通量q= 60 kW/m2，傾斜角度為0°。本文以方形微通道為例給出具體的分析，不同網格尺寸下加熱段出口的主流溫度和局部平均傳熱系數偏差如表2 所示。

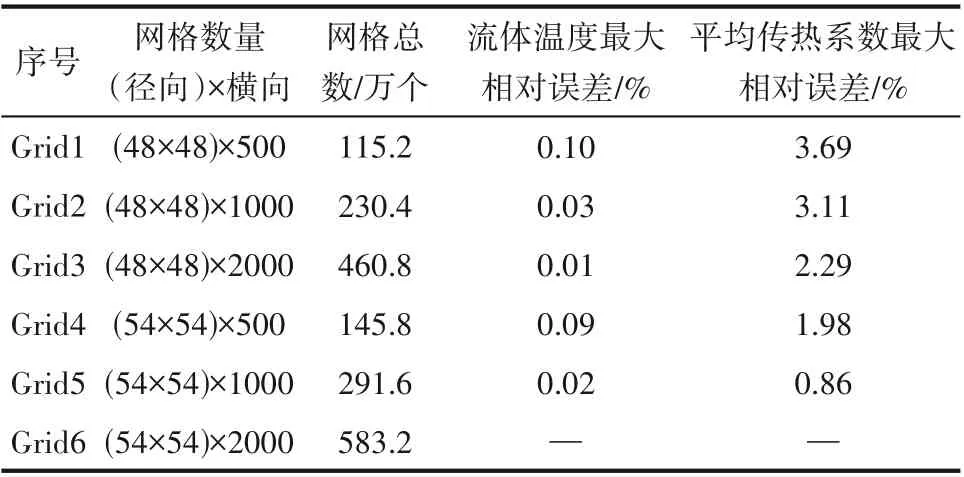
表2 不同尺寸網格下的流體溫度和平均傳熱系數偏差Table 2 Deviations of bulk temperature and average heat transfer coefficient under different grid sizes

由表2 可知，網格徑向尺寸和橫向尺寸均與計算結果的精度相關，但是6 種網格的模擬結果相差不大，以網格6為基準作對比，流體溫度最大相對誤差均小于0.10%，平均傳熱系數最大相對誤差均小于3.69%。考慮到計算時間和計算精度的均衡性，選取網格5 開展后續的模擬，可滿足計算精度的需求。同樣地，采取相同的方法進行半圓形微通道的網格獨立性檢驗，均能夠保證選用的網格滿足計算精度的需求。

1.4 求解方法與模型驗證

為獲取各項局部參數，沿流體流動方向建立多個截面，每個截面的主流溫度Tb定義為

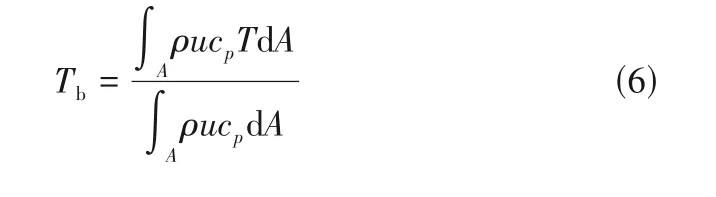
由于浮升力效應的影響，加熱管周向壁面溫度及對流傳熱系數均呈現出不均勻的特征。局部平均傳熱系數have、上壁面平均傳熱系數htop和下壁面平均傳熱系數hbottom分別定義為

其中，ρ為密度，kg/m3；u為速度，m/s；cp為比定壓熱容，J/(kg·K)；A為橫截面面積，m2；q為熱通量，kW/m2。

湍流模型驗證時，將模擬所得的局部平均傳熱系數have與Liao 等[33]、Wang 等[34]根據實驗數據提出的傳熱關聯式進行對比。Liao 等、Wang 等提出的傳熱關聯式均考慮了超臨界CO2在微細管道內流動時浮升力效應的影響，根據其適用條件，本文兩種管型湍流模型驗證基于的邊界條件均為：P= 8.0 MPa，Tin=305 K，G=1000 kg/(m2·s)，q=75 kW/m2，α=0°。由圖3 可看出，兩個換熱關聯式均能夠很好地預測超臨界CO2在方形微通道的換熱特性，由于模擬時管道形態及邊界條件與實際操作情況有偏差，在擬臨界溫度點附近誤差較大，但是最大相對誤差不超過±20%，屬于可接受的偏差范圍。采用相同的方法驗證SSTk?ω湍流模型對半圓形微通道的適用性，最大相對誤差不超過±15%，偏差范圍合理。

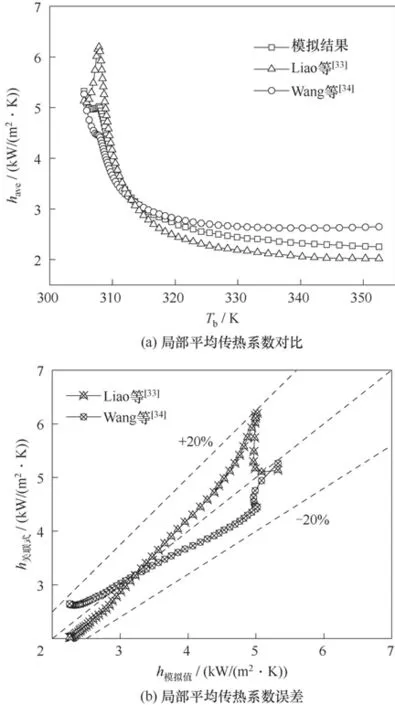
圖3 模擬結果與傳熱關聯式對比Fig.3 Comparisons of simulated results with predicted data from heat transfer correlations

2 結果與討論

2.1 傳熱系數

2.1.1 管型的影響 本節模擬工況以P=8.0 MPa，Tin= 303.15 K，G= 400 kg/(m2·s)，q= 60 kW/m2，α=0°為例分析管型對超臨界CO2流動換熱的影響。本文將工質主流溫度Tb＜Tpc的區域定義為類液區，將Tb＞Tpc的區域定義為類氣區。

圖4給出了常重力條件下方形微通道和半圓形微通道內沿流動方向局部平均傳熱系數have、上壁面平均傳熱系數htop、下壁面平均傳熱系數hbottom、主流溫度Tb的變化情況。可以看出，兩種管型中的三種傳熱系數和主流溫度沿流動方向的變化呈類似的趨勢。對比圖4(a)、(b)可知，同等運行參數下，在同一位置，兩種管型的流體溫度基本一致；然而，方形微通道的have大于半圓形微通道的have，且在加熱管的前半段，下壁面的傳熱增強程度比半圓形微通道內更大，此現象在擬臨界溫度附近尤為突出。在Lz= 500 ～800 mm 的管段，htop和hbottom之間的差值在方形微通道內逐漸縮小至零，而在半圓形微通道內始終存在，主要是由于半圓形微通道在重力方向上的結構不對稱性造成的。水平方向流動時，方形微通道的整體換熱效果優于半圓形微通道，故在下文的研究中，以方形微通道作為重點研究對象。

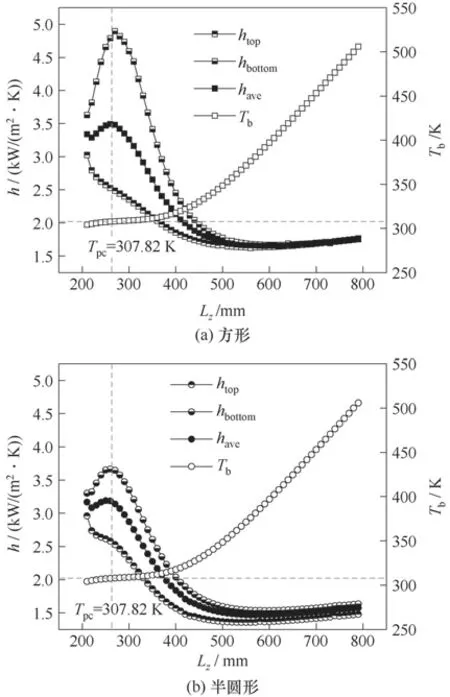
圖4 方管和半圓管的壁面平均傳熱系數和流體溫度（P=8.0 MPa,Tin=303.15 K,G=400 kg/(m2·s),q=60 kW/m2）Fig.4 Heat transfer coefficient and local bulk temperature in square and semicircular tubes

根據式（8）和式（9）關于htop和hbottom的定義，上、下壁面出現換熱不均勻現象的直接原因是Tw,top和Tw,bottom之間存在差異。圖5 給出了常、零重力兩種條件下，方形微通道內Tb/Tpc= 1.0 截面周向壁面溫度的分布情況。對比零重力條件下溫度分布呈現出的對稱性，可以看出常重力條件下超臨界CO2在水平方形微通道內流動換熱時，上、下換熱不均勻現象主要是重力造成的。

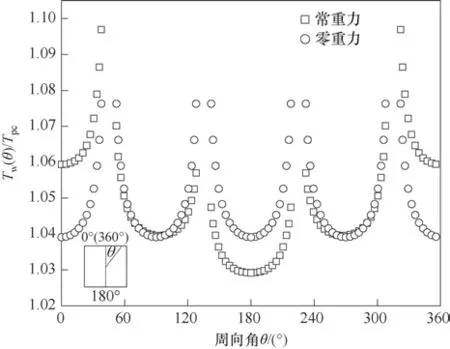
圖5 重力對壁面溫度的影響(P=0.8 MPa,Tin=303.15 K,q=60 kW/m2,G=400 kg/(m2·s))Fig.5 Effect of gravity on wall temperature

下面將著重探討常重力條件下熱通量、質量流量和傾斜角度對傳熱系數的影響。根據圖4(a)，在管道的后半段，即Lz= 500～800 mm 處，htop、hbottom與have之間的差別較小，故在下文分析運行參數對換熱的影響時，僅展示Lz=200～500 mm管段的特性。

2.1.2 熱通量和質量流量的影響 圖6 和圖7 分別給出了不同熱通量和質量流量條件下，三種壁面平均傳熱系數隨主流溫度的變化曲線。由圖6(a)和圖7(a)可知，在類液區，隨著熱通量的增大或質量流量的減小，htop和hbottom均逐漸減小，且兩者之間的差值逐漸增大，這意味著在主流溫度相同的位置，外壁面施加的熱量越高或單位時間內流過的流體越少，上壁面附近越容易聚集低密度的高溫流體，上、下壁面之間的溫差越大，換熱不均勻性越強。擬臨界溫度附近，在低熱通量（q=40 kW/m2）條件下，htop和hbottom變化趨勢類似，均能夠達到峰值，而在高熱通量（q≥60 kW/m2）條件下，htop隨主流溫度的增大處于下降的趨勢。在遠離擬臨界溫度的管段，htop與hbottom之間的差異逐漸縮小并趨于一致。由圖6(b)和圖7(b)可以看出，隨著熱通量的減小或質量流量的增大，have逐漸增大，這與Kumar等[13]在水平圓管內得出的結論基本一致。

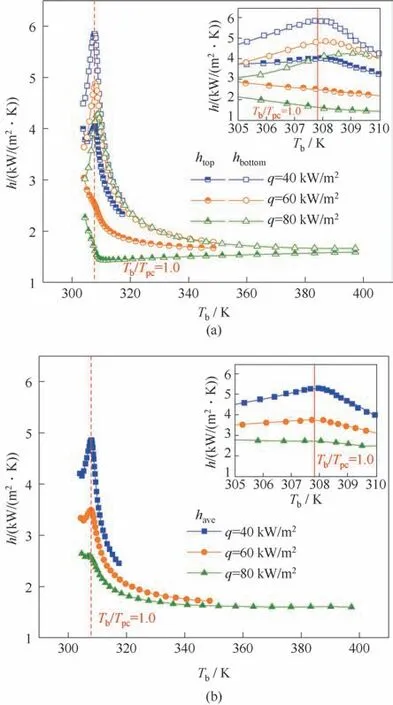
圖6 熱通量對傳熱系數的影響（P=8.0 MPa,Tin=303.15 K,G=400 kg/(m2·s)）Fig.6 Effect of heat flux on heat transfer coefficient

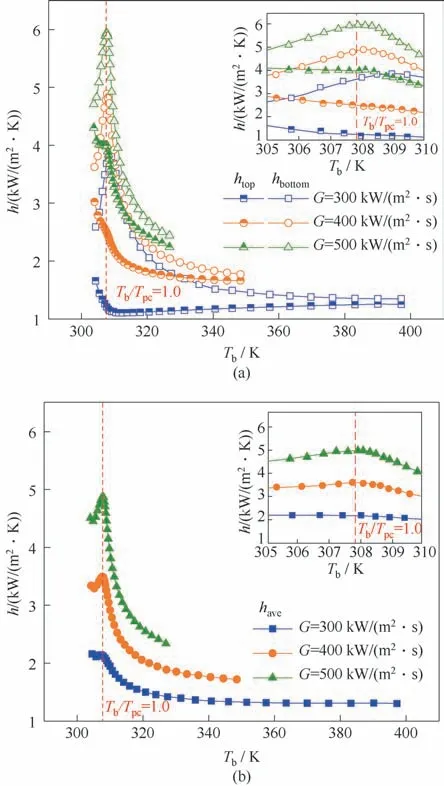
圖7 質量流量對傳熱系數的影響（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2）Fig.7 Effect of mass flow rate on heat transfer coefficient

2.1.3 傾斜角度的影響 為研究傾斜角度對換熱特性的影響，圖8 給出了七種傾斜角度條件下（α=0°、30°、60°、90°、?30°、?60°、?90°）三種壁面平均傳熱系數的變化曲線。由圖8(a)可以看出，除豎直流動（α= 90°和α= ?90°）外，其他5 種傾斜角度條件下均呈現出上下換熱不均勻的特點。當α= 0°時，htop與hbottom之間的差值最大，隨著夾角α絕對值的增大，htop與hbottom之間的差值減小，且當豎直向上或向下流動時，兩者之間的差值基本為零。根據圖8(b)，have在豎直向下流動時最大，在豎直向上流動時最小，在水平流動時居中。整體表現為，一定壓力條件下，在擬臨界溫度附近，夾角α的數值越小，局部平均傳熱系數越大，但是在遠離擬臨界溫度的區域，傾斜角度對局部平均傳熱系數的影響較小。

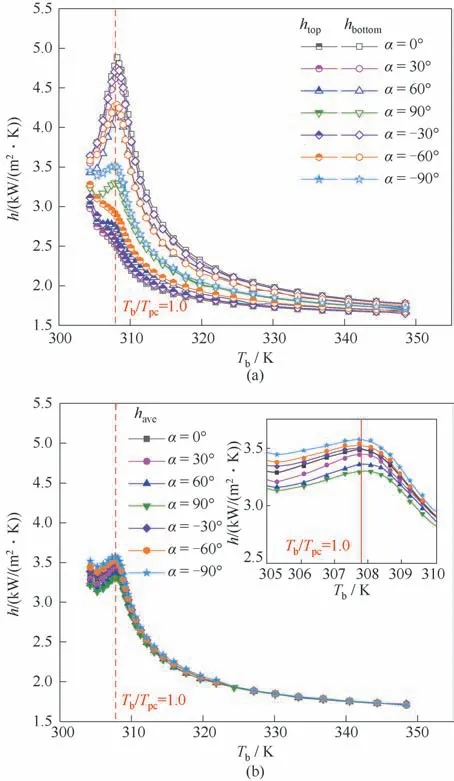
圖8 傾斜角度對傳熱系數的影響（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2,G=400 kg/(m2·s)）Fig.8 Effect of inclination angle on heat transfer coefficient

2.2 浮升力效應

2.2.1 常重力條件下的基本特征 本節從浮升力效應的角度分析了常重力條件下微通道內超臨界CO2的傳熱機理。同樣地，以模擬工況P=8.0 MPa，Tin= 303.15 K，G= 400 kg/(m2·s)，q= 60 kW/m2，α=0°為例進行具體的分析。圖9 給出了常重力條件下方形微通道內兩個特征截面的溫度分布云圖和徑向速度矢量圖，在Tb/Tpc=1.0 截面，流體溫度上下分布不均勻，且存在著明顯的二次流現象，管道上半部分的流體溫度高于下半部分，尤其是上壁面附近，大量的低密度高溫流體在此處聚集，使得外壁面被施加的熱量在向主流流體徑向傳遞時熱阻增加，降低了換熱水平。在Tb/Tpc= 1.05 截面處，流體溫度上下分布的不均勻性及二次流強度均減弱，這與圖4(a)所示的htop與hbottom之間的差值隨主流溫度的增大而減小相對應。如圖9 所示，方形微通道的四個尖角處，流體溫度達到整個截面的峰值，在遠離擬臨界溫度的管段，尖角處的徑向速度也較小，低密度高溫流體在此處更易聚集，不利于整體的熱量傳遞。在實際工程應用中，考慮到換熱效率及運行安全性，應最大程度地避免尖角的出現。

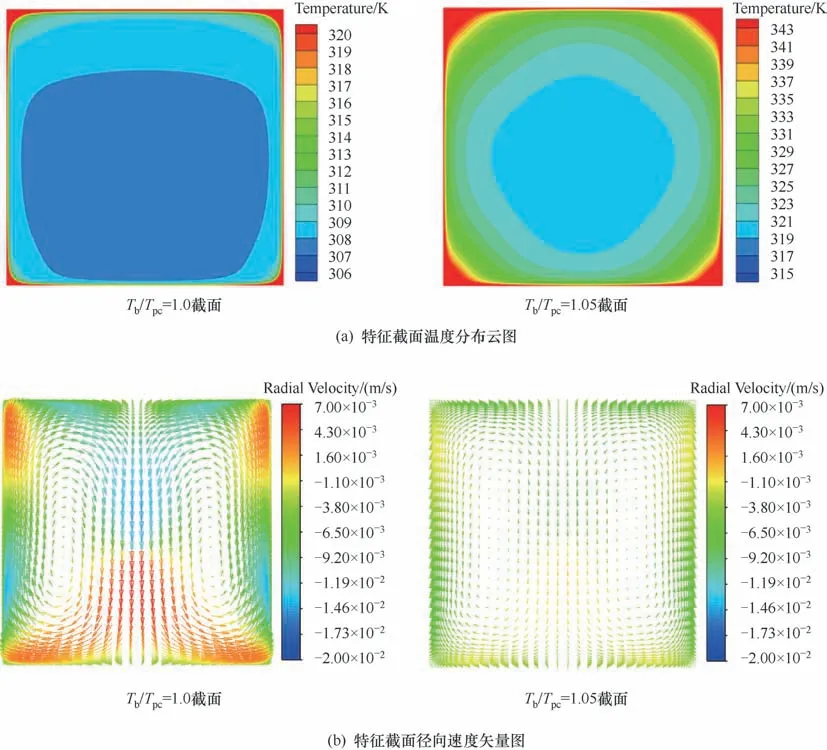
圖9 特征截面處的典型參數分布Fig.9 Distribution of typical parameters at characteristic cross?sections

圖10 給出了常重力條件下方形微通道內兩個特征截面的軸向速度和湍動能徑向分布曲線，受浮升力的影響，在擬臨界溫度附近，軸向速度的最大值及湍動能的最小值不再位于管道中心，而是在管道的下半部分，且上壁面附近的流體軸向速度和湍動能低于靠近下壁面的流體，這表明上壁面附近的流體并不能及時地將熱量沿著流動方向向前傳遞。在遠離擬臨界溫度的管段，截面上的軸向速度和湍動能的數值上下對稱相等，浮升力的影響基本可以忽略。

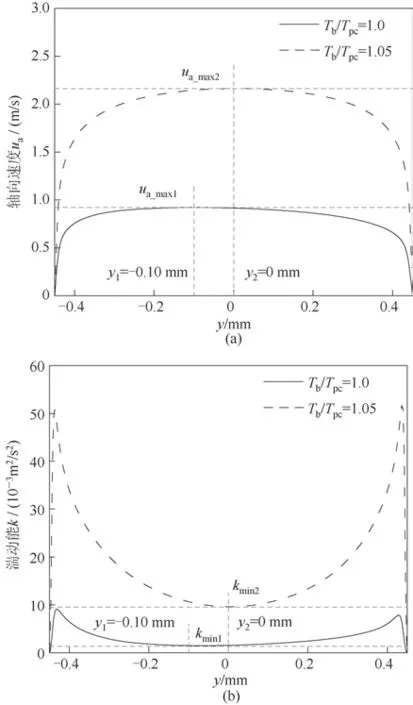
圖10 特征截面處的軸向速度和湍動能徑向分布曲線Fig.10 Radial distribution curves of axial velocity and turbulent kinetic energy at characteristic cross?sections

對于水平管道內的流動，浮升力參數Gr/Re2得到了廣泛應用，很多學者[6,11,33]認為當Gr/Re2＞0.001時，浮升力的作用不能忽略，本文采用Gr/Re2定量表征流體流動過程中浮升力效應的影響。同時，為表征沿流動方向二次流強度的變化，引入二次流動能參數Ke，其表達式為[35?36]

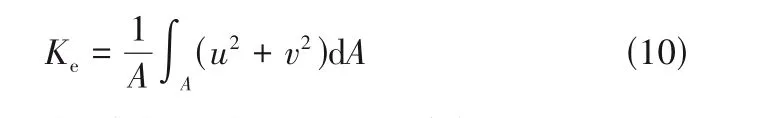
式中，u和v分別表示方形微通道截面在x和y方向上的速度分量。圖11 給出了方形微通道和半圓形微通道內Gr/Re2和Ke的沿程變化曲線，可以看出，在方形微通道的后半段，即Lz=400～800 mm 處，浮升力的影響基本可以忽略，且Tb/Tpc=1.05 截面恰好處于該范圍。由圖11(a)可以看出，兩種管型在沿程同一位置的浮升力參數數值基本相同。根據圖11(b)，二次流強度在類液區增加較快，在主流溫度升至擬臨界溫度前達到峰值，在類氣區隨主流溫度的增大逐漸減小并趨近于0。在類氣區，同等運行參數下，在同一位置，半圓形微通道內的二次流強度高于方形微通道，這說明半圓形微通道在類氣區換熱效果較差是由于較強的二次流造成的。不難發現，二次流強度Ke比浮升力參數Gr/Re2在分析管型對傳熱的影響時更加適用。

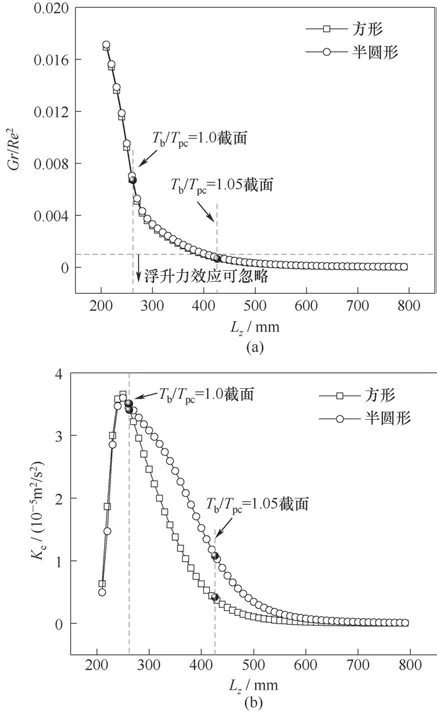
圖11 沿程浮升力參數和二次流強度變化曲線（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2,G=400 kg/(m2·s)）Fig.11 Variation curves of buoyancy parameter and secondary flow intensity

2.2.2 熱通量和質量流量的影響 熱通量和質量流量對沿程浮升力參數及二次流強度的影響如圖12和圖13所示，隨著熱通量的增大或質量流量的減小，相同主流溫度對應的截面上浮升力參數和二次流強度的數值逐漸增大，說明有更多的低密度流體沿管壁流至上壁面附近，這也是導致上、下壁面平均傳熱系數差值大的關鍵因素。在類液區，隨著主流溫度的增大，二次流強度顯著增加，流體處于自然對流和強迫對流都存在的混合對流狀態，浮升力效應不可忽略；在類氣區，隨著主流溫度的升高，自然對流的作用逐漸減弱，二次流強度先急劇下降，再逐漸趨于平緩；當高于一定的主流溫度時，浮升力效應基本可以忽略，且熱通量越小或質量流量越大，越容易達到閾值。

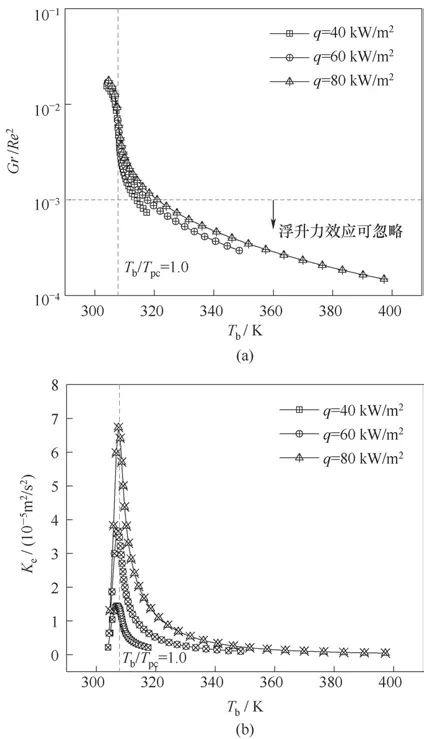
圖12 熱通量對浮升力參數和二次流強度的影響（P=8.0 MPa,Tin=303.15 K,G=400 kg/(m2·s)）Fig.12 Effect of heat flux on buoyancy parameter and secondary flow intensity

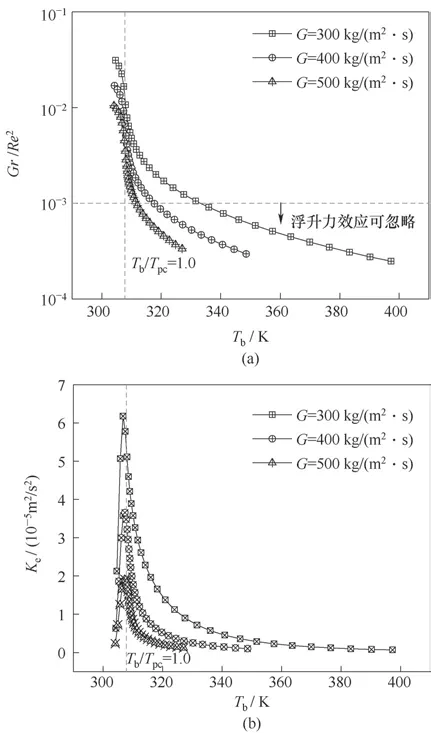
圖13 質量流量對浮升力參數和二次流強度的影響（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2）Fig.13 Effect of mass flow rate on buoyancy parameter and secondary flow intensity

2.2.3 傾斜角度的影響 圖14 給出了七種傾斜角度條件下沿程二次流強度的分布及Tb=Tpc截面的壁溫分布曲線，可以看出，豎直方向流動時，由于浮升力方向和流體流動方向平行，二次流強度接近于零，且在Tb=Tpc截面，壁面溫度的分布關于管道中心點中心對稱。非豎直方向流動時，在擬臨界溫度附近，二次流強度的大小表現為：0° ＞30° ＞?30° ＞60°＞?60°，即傾斜角度越偏離水平方向，二次流強度越小，當夾角α的絕對值相等時，傾斜向下流動時的二次流強度明顯小于傾斜向上流動時的工況。在遠離擬臨界溫度的區域，二次流強度均較小，不同的是，在該區域，傾斜向上和傾斜向下之間的差異不再明顯。在Tb=Tpc截面，上、下壁溫的差值與二次流強度有關，二次流強度越大，上、下壁溫的差值越大。相同主流溫度所在的截面上二次流強度越大，說明在浮升力的作用下，高溫低密度流體沿著壁面向上表面附近聚集的趨勢越強烈，上、下壁面的溫度差異越明顯，尤其是在擬臨界溫度附近，上下換熱的不均勻性越容易突顯。

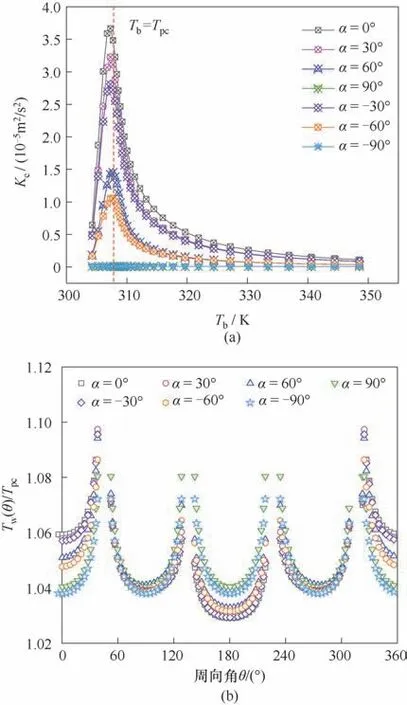
圖14 傾斜角度對二次流強度和壁面溫度的影響（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2,G=400 kg/(m2·s)）Fig.14 Effect of inclination angle on secondary flow intensity and wall temperature

3 結 論

本文對微通道內超臨界CO2的流動換熱特性進行了數值模擬，在對比分析方形和半圓形微通道換熱效果差異的基礎上，進一步探討熱通量、質量流量和傾斜角度對方形微通道內換熱特性的影響，得出主要結論如下。

（1）水平方向流動時，方形微通道整體換熱效果優于相同水力直徑的半圓形微通道。

（2）常重力條件下，非豎直方向流動時，重力方向上存在明顯的換熱不均勻現象，上壁面附近聚集更多低密度的高溫工質，流體的軸向速度及湍動能處于較低水平，抑制了管壁熱量的有效傳遞，沿程二次流強度的大小是其重要的影響因素，浮升力效應不可忽略。

（3）增大熱通量、減小質量流量或減小夾角α的絕對值時，二次流強度顯著增加，浮升力效應增強，htop與hbottom之間的差值增大。減小熱通量、增大質量流量或減小夾角α的數值，有助于提升加熱管的整體換熱水平。

符 號 說 明

Gr——Grashof數

Lz——z軸方向上從原點到所在位置的長度，mm

Re——Reynolds數

下角標

ave——壁面平均值

b——主流體

bottom——下壁面

top——上壁面