基于分子指紋和拓撲指數的工質臨界溫度理論預測

任嘉輝，劉豫，劉朝，劉浪，李瑩

（1 重慶大學低品位能源利用技術及系統教育部重點實驗室，能源與動力工程學院，重慶 400030； 2 污染控制與資源化研究國家重點實驗室，江蘇南京 210023； 3 中國核動力研究設計院中核核反應堆熱工水力技術重點實驗室，四川成都 610213）

引 言

臨界溫度(Tc)作為工質能維持液相的最高溫度，是建立狀態方程的基礎，也可以用于計算工質其他物性如焓、熵、比熱容、黏度、熱導率等。同時，臨界溫度是超臨界萃取過程中的重要參數。因此，獲取工質準確的臨界溫度具有重要的科學意義和工程價值[1?5]。實驗是獲取臨界溫度最有效的方式。然而由于實驗研究代價高昂、復雜性高，無法僅依靠實驗手段獲得工質的臨界溫度。因此，有必要提出一種能夠準確預測工質臨界溫度的理論模型。

臨界溫度的預測方法主要包括經驗公式法、狀態方程法和定量結構?性質關系法(quantitative structure?property relationship, QSPR)。經驗公式法采用一些易于測量的參數，如沸點、密度等，建立相應的關聯式得到臨界溫度。Reid 等[6]最早提出了臨界溫度與沸點的關聯式Tc=1.5Tb。周傳光等[7]基于沸點與對比密度，提出了部分化合物臨界溫度的關聯式，平均偏差為1.35%。王新紅等[8]以沸點、對比密度、相對分子質量為參數，提出了一個新的有機物臨界溫度計算模型，平均偏差為2.36%。經驗公式法形式簡單、計算精度較高，但缺乏理論基礎。狀態方程法可以基于pVT數據，擬合獲得工質狀態方程中相應參數，而后反推得到物質的臨界溫度。例如，Kontogeorgis 等[9]采用狀態方程法估算了6 種烷烴的Tc，絕對平均偏差均在2%以內。Hsieh 等[10]依據同樣的思路，首先獲得Peng?Robinson(PR)狀態方程的參數，進而得到392種純物質的臨界溫度，平均偏差為5.4%。狀態方程法需要已知工質pVT數據，且計算流程復雜，適用于密度數據較為豐富的物質。定量結構?性質關系法(QSPR)根據分子結構?物質性質之間的構效關系，對物質相關性質進行建模和預測。基團貢獻法是QSPR 中最常用的一種方法，包括經典的Lydersen 法[11]、Joback 法[12]等。這些方法假設分子性質為各基團貢獻的線性加和，而基團貢獻度在不同分子中保持不變。這種線性加和的方法使用較方便，但沒有考慮不同基團的位置信息，導致該方法不能有效區分同分異構體。盡管 后 續 的 一 些 方 法 如Constantinou?Gani 法[13]、Marrero?Pardillo 法[14]等，通過引入多級基團和鍵貢獻在一定程度上緩解了上述缺陷，但適用范圍依然有限。綜合分析以上方法可知，現有模型無法對常見工質進行準確估算，須采用新的思路，以實現對包括同分異構體工質在內的常見工質臨界溫度的精準預測。

分子結構描述符[如分子指紋(molecular fingerprints, MF)[15]、拓撲指數(topological index, TI)[16]等]作為一種將分子結構編碼為結構化數據的方法，可以將一種物質與其他物質進行明確區分。將分子描述符的概念引入QSPR 模型，有望解決工質同分異構體的區分問題。在實際使用中，分子描述符通常與機器學習方法(machine learning, ML)相結合，以構建物質特性預測模型[17?19]。近年來，隨著計算機性能的不斷提高，有學者將分子描述符和機器學習應用于工質物性[20?24]的預測，預測效果良好。

本研究受上述分子描述符工作的啟發，首先以分子指紋表征分子結構，并借助機器學習算法建立16 種臨界溫度的QSPR 預測模型。此外，為了進一步提升本文模型的預測精度，本研究還將分子指紋與拓撲指數相結合，得到新的MF+TI?ML 模型(以分子指紋和拓撲指數表達分子結構，結合機器學習算法建立模型)，以期取得良好的預測效果。

1 方 法

1.1 數據庫的搭建

本研究中工質的臨界溫度實驗數據取自物理性質設計研究所(DIPPR?801)[25]及相關文獻[26]。根據實驗數據不確定度對其進行篩選后，獲得了155 種工質的Tc(本文所涉及工質的詳細信息，參見文末附錄)。搭建的數據庫中，臨界溫度的范圍分布在190.56～583.00 K。數據庫中工質可分為五種：烷烴、烯烴、鹵代烷烴、鹵代烯烴、醚類。為提升模型泛化能力，從每種類型工質中選取其中70%的數據點進入訓練集，剩下的30%作為測試集。訓練集用于建立工質臨界溫度的模型，測試集用于評估模型的預測性能。

1.2 分子指紋的生成

通過ChemDraw 程序獲得工質分子的線性輸入規范(simplified molecular input line entry system,SMILES)，隨后利用在線轉換工具ChemDes[27]將SMILES 字符串轉換為相同長度的二進制位串(即分子指紋)。為了研究不同長度/類型的指紋對QSPR模型性能的影響，本文選擇了計算四種分子指紋，包括兩種Key 型指紋：MACCS(166 位)和Pubchem(881 位)，一種Path 型指紋：Extended(1024 位)和一種Circular型指紋：Morgan(2048位)。

1.3 回歸算法的選擇

本文使用了四種機器學習算法，包括支持向量回 歸(support vector regression, SVR)、回 歸 樹(regression tree, RT)、隨機森林(random forest, RF)以及多層感知機(multi?layer perceptron,MLP)。

支持向量回歸通過核技巧將非線性數據映射到高維空間中，將非線性關系轉換為線性的形式，其精度取決于參數的選擇，例如核函數、寬度系數γ、不敏感損失系數ε、懲罰系數C等[28]。在本文中，將采用5折交叉驗證和網格搜索確定參數的最佳組合。決策樹(decision tree, DT)利用多節點的樹結構來描述各變量與目標之間的非線性關系，回歸樹是決策樹的回歸版本。由于樹模型具有較高的方差，可能導致結果不穩定，基于樹模型的集成學習算法隨機森林相對樹模型有較大的改進[29]，在物性預測中應用較多。 人工神經網絡(artificial neural network,ANN)模擬神經系統的結構，通過不斷調整神經元間的權重和偏差，使整個網絡能更好地擬合數據[30?34]。多層感知機(MLP)是一種前饋神經網絡，通過相互連接的人工神經元和復雜的拓撲結構來模擬非線性關系[35]。本文利用深度學習庫Keras 搭建了具有雙隱層的MLP，并通過試錯法確定了神經元數、激活函數、學習率的最優組合。

1.4 評估指標的選擇

本文選用均方根偏差(RMSE)、絕對平均偏差(AAD)、決定系數(R2)評估模型的預測性能，相關定義式如下。

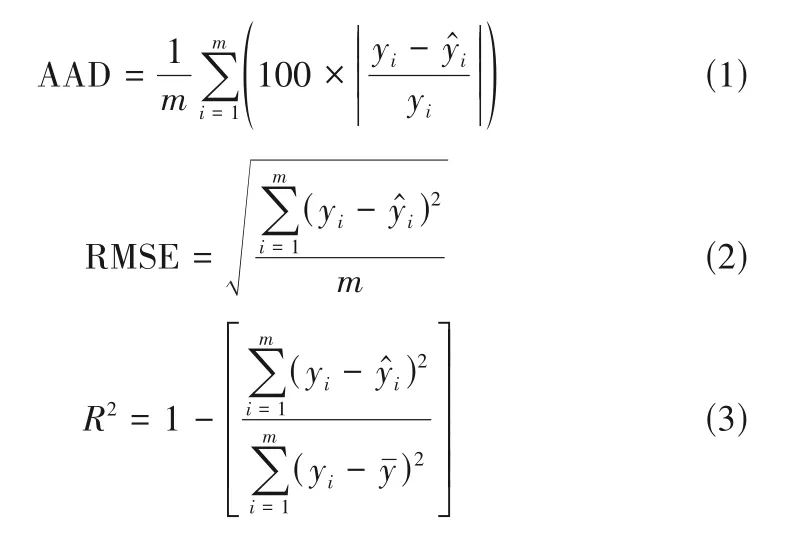
式中，m表示樣本個數；yi和?分別表示工質i臨界溫度的實驗值和預測值；yˉ表示臨界溫度實驗數據平均值。將評估指標應用于測試集時，RMSE、AAD越低，R2越高，模型的表現越好。

2 實驗結果與討論

2.1 模型的建立與評估

將四種分子指紋(MACCS、Pubchem、Extended、Morgan)分別用作四種機器學習算法(SVR、RT、RF、MLP)的輸入特征，得到16 種臨界溫度的QSPR 模型。各模型在測試集中的預測性能(以絕對平均偏差AAD為評價指標)如圖1所示。

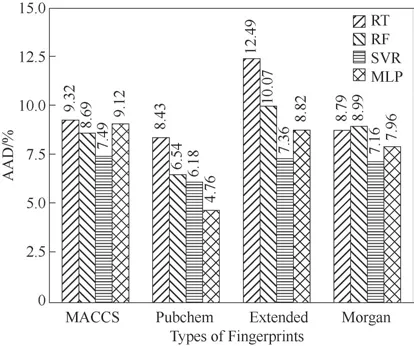
圖1 以不同指紋為輸入的各QSPR模型的預測精度Fig.1 Prediction accuracy of QSPR models with different fingerprints as inputs

從圖1 可以看出，以MACCS 指紋為輸入特征的模型預測性能較差，其中表現最好的MACCS?SVR(以MACCS 指紋為輸入，結合SVR 建立的模型)在測試集中的絕對平均偏差(AAD)也僅達到了7.49%。其原因是MACCS指紋長度過短，包含的結構信息有限，導致工質某些結構片段并不包含于MACCS指紋中。因此，以短位數的MACCS 為輸入，模型預測精度并不高。

Extended指紋結合SVR算法建立的模型在測試集的AAD 為7.36%。這是因為在ChemDes 中，Extended 指紋最大路徑長度默認設置為5 (即結構片段包含的最大鍵數為5)，導致許多線性路徑大于5 的分子具有相同的Extended 指紋。由于缺乏碳鏈長于5 的工質Tc的實驗數據，如果提高路徑最大長度，特征維度會急劇增加，從而造成模型過擬合。因此目前來看Path 型指紋不是建立工質QSPR 模型的最優選擇。

Circular 型指紋Morgan 作為一種立體型指紋長度最長，包含的結構信息也最多，因此可以有效地表征分子結構，進而有效區分工質同分異構體。綜合來看，雖然以Morgan 指紋為輸入特征的模型預測性能要比上述兩種類型的指紋好，但仍不理想。其原因可能是位數過長導致了模型過擬合，因而Morgan 指紋也不適用于搭建樣本數較少的QSPR模型。

Pubchem?MLP 模型(Pubchem 指紋結合MLP 算法建立的模型)在訓練集、測試集的AAD 分別為1.12%、4.76%。相比其他分子指紋而言，基于Pubchem 指紋的QSPR 模型預測表現最好。這說明Pubchem 指紋可以合理表征工質的結構信息，從而在有限的訓練樣本中有效建立分子結構與臨界溫度之間的構效關系，準確預測工質臨界溫度。針對本文所研究的155 種工質，Pubchem?MLP 模型在工質臨界溫度實驗值和計算值的比較如圖2所示。

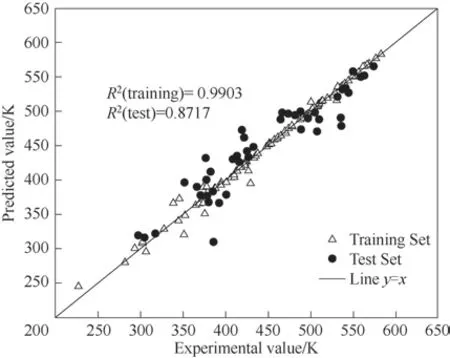
圖2 Pubchem?MLP模型在工質臨界溫度實驗值和計算值的比較Fig.2 Comparison between experimental and caculated values of Pubchem?MLP model

從結果來看，四種ML 算法建立的模型對工質臨界溫度的綜合預測效果排序如下：SVR ＞MLP ＞RF ＞RT。SVR 模型預測精度最高且表現穩定。基于集成算法RF 的模型相比RT，在預測精度上有了明顯的提高，但和SVR仍有較大差距。

2.2 模型的優化

Pubchem 指紋可以很好地表達工質結構。但由于該類型指紋需要預先指定子結構，可能會造成工質中極少數同分異構體(如順反異構體)無法區分的問題。因此本文考慮在分子指紋的基礎上添加拓撲指數，以“分子指紋+拓撲指數”(MF+TI)作為新型分子結構描述符，采用效果較好的SVR 和MLP 算法，以期完全解決區分工質中同分異構體的問題。

拓撲指數是一種量化分子結構的指標，通過對表征分子圖的矩陣執行數值運算獲得。這里引入拓撲指數(molecular topological index,MTI′)，在MTI′的基礎上添加幾何校正數(geometric modification,GM)區分工質中的同分異構體，拓撲指數S的計算公式[16]如下：

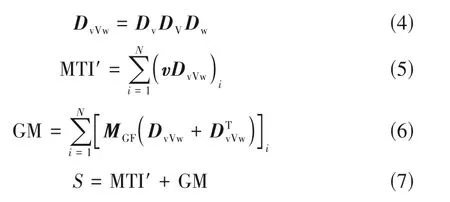
式中，Dv、DV、Dw分別表示工質結構的價矩陣、頂點權重矩陣、鄰接矩陣；N表示分子的原子總數；v表示價向量；MGF是用以區分異構體的對角矩陣。文末附錄給出了拓撲指數的具體計算流程和案例。

采用新型描述符后兩種模型的回歸和預測性能如圖3、圖4 所示。可以看出引入拓撲指數S后，模型的預測精度明顯提升。Pubchem+TI?SVR 模型(新型描述符輸入SVR 算法建立的模型)在測試集的決定系數R2提高到0.8426，而Pubchem+TI?MLP 模型(新型描述符輸入MLP 算法建立的模型)在測試集的AAD 降低至3.99%，R2提高到0.9143。對比圖2、圖4 可以發現，相比Pubchem?MLP 模型，Pubchem+TI?MLP 模型預測性能明顯提高。這表明引入拓撲指數得到的新型描述符可以很好地解決區分工質中同分異構體的問題，提升模型的預測性能。

圖3 Pubchem+TI?SVR 模型在工質臨界溫度實驗值和計算值的比較Fig.3 Comparison between experimental and caculated values of Pubchem+TI?SVR model

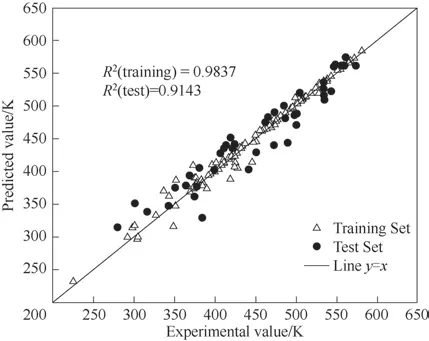
圖4 Pubchem+TI?MLP模型在工質臨界溫度實驗值和計算值的比較Fig.4 Comparison between experimental and caculated values of Pubchem+TI?MLP model

表1 給出了本文搭建的Pubchem+TI?MLP 模型在工質各數據集、各物質體系預測值和實驗值的AAD。從表中可以看出，新提出模型對烷烴類工質臨界溫度的回歸和預測都具有很高的精度，分別達到了0.90%和1.65%。模型對烯烴類工質的擬合回歸效果很好，但預測效果較差。醚類、鹵代烷烴類、鹵代烯烴類工質的計算精度相比上述兩類更低。從整個數據集來看，五種類型工質的絕對平均偏差均低于3%，取得了很好的計算效果。

表1 本文模型在各數據集、各物質體系的AADTable 1 AAD for each dataset and category of working fluids

圖5 給出了155 種工質的相對偏差(ARD)分布情況，相對偏差的定義如式(8)所示：

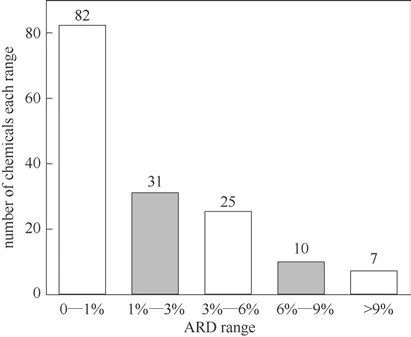
圖5 工質臨界溫度ARD分布情況Fig.5 Distribution of ARD for Tc of working fluids

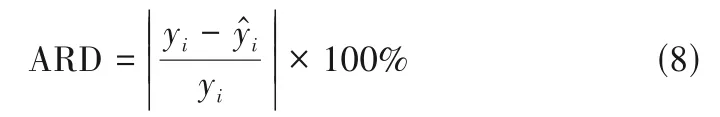
其中ARD＜3%的工質有113 種，占比72.9%，ARD＞9%的工質僅7種，最大偏差為15.98%。

2.3 模型的對比

將新提出模型的計算結果與現有其他方法進行對比，用于對比的經典方法列在表2中，模型的比較結果如表3 所示。從表3 中可以看出，本文模型的計算精度最高，Lydersen 法和Joback 法次之，C?G法精度最低。基于沸點實驗值的Joback 法計算工質Tc精度很高。但必須注意的是，并非所有工質都具有準確的沸點數據。當使用估算的沸點值(Testb)計算時，Joback 法的計算效果明顯降低。C?G 法不需要使用沸點值，但該方法對工質臨界溫度的預測精度較低。K?R 法將臨界溫度與分子量(Mw)、沸點關聯，并給出了一個簡單的線性方程，估算效果較好。然而，這種關聯缺乏理論基礎，普適性較差。綜合來看，本文提出的Pubchem+TI?MLP 模型基于分子結構計算工質的臨界溫度，不僅無須沸點值，還獲得了最高的計算精度。

表2 現有預測臨界溫度的方法Table 2 Existing method for estimation of critical temperature

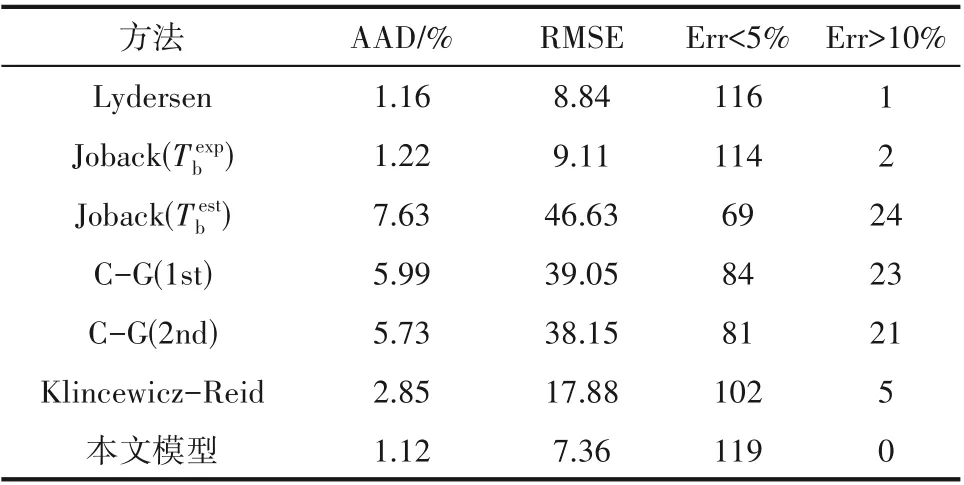
表3 提出模型與以往方法計算效果的對比Table 3 The comparisons between proposed model and previous methods

為了進一步驗證本文新提出模型和C?G 法在區分同分異構體性能上的差異，表4 給出了C?G 二級基團貢獻法和本文模型在區分各類同分異構體(包括順反異構、位置異構和碳架異構)上的案例，其中表示本文模型計算值表示二級C?G 法計算值。

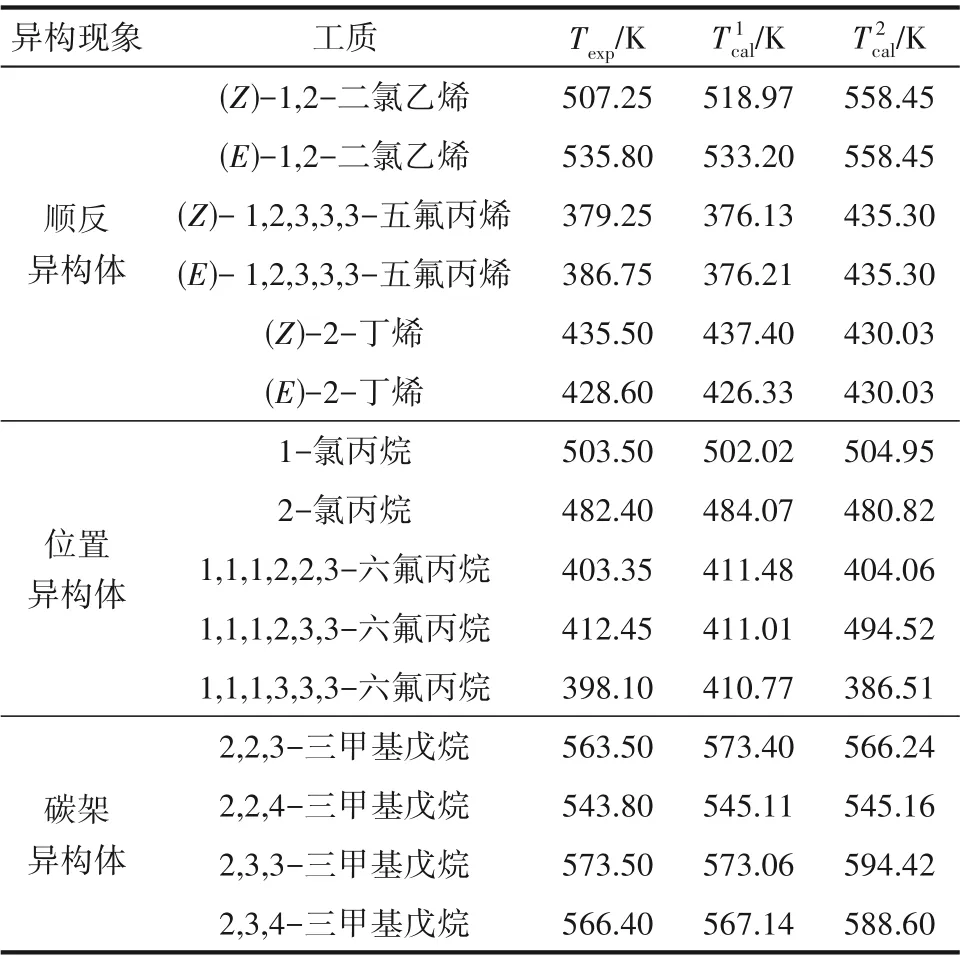
表4 C-G法和本文模型對同分異構體的區分案例Table 4 Samples of isomers for the comparison of C-G method and the proposed model

從表4 中可以看出，本文模型對于各類同分異構體的臨界溫度都取得了良好的預測精度。而C?G 法對于所有順反異構體的臨界溫度預測結果完全一致，這表明C?G法無法區分順反異構體。

表5給出了本文模型和C?G 二級基團貢獻法對155 種工質中三類同分異構體計算結果的統計結果。從表5 中可以看出，C?G 法在碳架異構體的計算表現良好，37 種碳架異構體臨界溫度的AAD 為1.87%，但是由于不能辨別順反異構，對10種順反異構體的計算精度較差。在位置異構體臨界溫度的計算上，C?G 法的精度也較低。而本文提出的Pubchem+TI?MLP 模型不僅可以有效區分工質中存在的各類同分異構體，在計算精度上也遠高于C?G法。本文模型對順反異構體、位置異構體、碳架異構體臨界溫度計算值和實驗值的AAD 分別為2.35%、2.51%、0.87%。

表5 C-G法和本文模型計算同分異構體的統計結果Table 5 Statistical parameters of C-G method and the proposed model for the isomers

3 結 論

本文基于分子指紋和拓撲指數，采用機器學習算法建立了工質臨界溫度的Pubchem+TI?MLP 模型。將新模型應用于155種常見工質的臨界溫度預測中，取得了良好的計算精度，針對測試集預測的絕對平均偏差為3.99%。通過與經典模型的比較可以得出，新模型不僅可以有效區分工質中各類同分異構體，其計算精度相比現有模型也更高。通過對模型進一步分析還可看出，對指紋長度的選擇，必須綜合考慮樣本總數以及數據集包含的物質種類。在指紋類型的選擇上，Key 型指紋Pubchem 雖然在本文工質的臨界溫度預測上表現最好，但其自身不能區分少數順反異構體，需要引入拓撲指數以提高區分能力。長度更長的Path 型和Circular 型指紋對同分異構體的區分能力更好，但不適用于樣本數少的數據集。隨著以后工質實驗數據的不斷補充，可考慮使用更長的分子指紋搭建性能更加優異的QSPR模型。

圖A1 本文模型計算流程示意圖
Fig.A1 Flow chart of the calculation of the proposed model

以1，1，1，2，3，3，3?七氟?2?甲氧基丙烷（E347mmy1）為例，其分子結構如圖A2 所示，通過ChemDraw 轉換獲得E347mmy1 的SMILES 為COC（C（F）（F）F）（C（F）（F）F）F，ChemDes轉換分子線性輸入規范獲得Pubchem指紋[00100…01000…00000]，通過查詢樣例文件，獲得其拓撲指數值15420，將Pubchem 和拓撲指數組合輸入到本文模型中，得到E347mmy1 的臨界溫度計算值436.41 K，其實驗值為433.95 K。

圖A2 E347mmy1的分子結構
Fig.A2 The molecualr structure of E347mmy1