機理與數據驅動的電站鍋爐SCR催化劑壽命預測模型研究

胡佳穎，喻聰，王子良, 司風琪

(1.江漢大學智能制造學院，武漢 430056；東南大學能源與環境學院，南京 210096)

在我國，燃煤電廠是氮氧化物(NOx)的主要排放源之一，它會對環境和人體健康造成惡劣影響。目前，電站鍋爐普遍采用選擇性催化還原法(Selective Catalytic Reduction，SCR)進行煙氣脫硝。該方法是在催化劑的作用下，利用NH3將NOx還原為無污染的N2和H2O。其中，催化劑是SCR系統的核心裝備，成本最高，且直接影響脫硝效率[1]。廠家保證的催化劑壽命約為24 000小時，但電廠實際氣、固兩相流環境復雜，燃用煤種、運行方式、尺寸結構等諸多因素的不同會使催化劑的劣化趨勢千差萬別[2-3]。據統計，我國每年需更換的SCR催化劑體積約10～20萬m3，按1.5萬元/m3的平均單價核算，總價值約15～30億元。過早的換裝會造成催化劑的浪費與成本的損失，而過晚的換裝則會引起電站NOx排放濃度超標及氨逃逸過大，從而影響機組運行的環保性和安全性[4-6]。因此，催化劑的壽命預測有著重要意義。

傳統的催化劑壽命評價方法是實驗室檢測[7-8]，該方法是利用機組檢修期間從爐內抽取催化劑樣本塊，并帶回實驗室檢驗活性。然而，火電機組一年一小修、四年一大修的檢修周期決定取樣的時間點較少，不足以支撐催化劑3～5 a生命周期內活性劣化趨勢的精確描繪，且爐內大截面煙道存在煙氣的不均勻性，所抽取催化劑樣本塊的活性無法代表整個SCR反應器的脫硝能力，這都會影響評價結果的可信度。為解決這些問題，宋寶玉等[9-10]提出了基于現場性能試驗的脫硝裝置潛能預測，以對SCR反應器宏觀性能進行直接衡量，解決了傳統實驗室檢測法樣本代表性不足的問題，且檢測次數不再受機組啟停影響。然而，現場性能試驗成本較高，且為滿足每次試驗所需的煙氣條件，均需向電網申請穩定發電負荷，這將給承擔調峰調壓任務的火電機組增加額外負擔，因此該方法的預測精度同樣會受到試驗次數的影響。為進一步降低預測成本，學者們又提出基于歷史運行數據的催化劑壽命評估方法。一部分學者直接采用機器學習算法評估催化劑的活性[11-14]，而另一部分學者將數據挖掘和機理建模相結合，即首先建立催化劑動力學模型[15]或考慮堵塞、磨損、中毒等因素的綜合失活機理模型框架[16]，再利用電站SCR煙氣脫硝系統實際運行數據對模型參數進行辨識，以得到催化劑的活性劣化模型。然而，目前尚未見將這兩種模型進行對比與分析的研究。

本文以某電廠SCR脫硝系統3年歷史運行數據為樣本，通過建立2種異常值剔除程序，對比3種穩態樣本識別算法，建立了大數據過濾器，獲得了高質量穩態樣本集。在此基礎上，采用BP神經網絡將脫硝效率修正到同一運行水平，以表征催化劑健康狀態，并對比了機理模型及ARIMA模型對催化劑劣化趨勢的預測精度，進而分析了誤差的原因。

1 算法流程

本文以某660 MW電站燃煤鍋爐SCR系統單側反應器3年歷史運行數據為樣本。算法流程為：

Step1：利用統計法標記停滯點和超限數據。利用一種基于t檢驗和兩種基于R檢驗的方法，標記出非穩態數據樣本。并剔除原始數據中所有異常值和非穩態數據，得到穩態樣本集；

Step2：分別采用10 d、20 d、30 d三種時間步長整理出按時間排列的穩態數據子集，在單個時間步長內，假設催化劑壽命變化不大，并基于每個步長區間的數據，分別利用BP神經網絡建立脫硝效率與運行工況的靜態關系模型；

Step3：基于Step4的關系模型，將每個時間步長的脫硝效率修正到同樣的工況水平，此時脫硝效率的變化可表征催化劑宏觀性能的變化。

Step4：分別采用機理模型和ARIMA模型對各時間步長的催化劑宏觀性能點進行回歸，建立催化劑性能劣化模型。

2 大數據過濾器

2.1 異常值剔除

數據挖掘前，對異常值進行甄別并剔除。異常值包括由機組停機或數據傳輸故障引起的停滯點數據和粗大誤差數據。粗大誤差數據通過統計法及經驗設置上下限進行過濾，各參數限值如表1所示。

以入口NOx濃度為例，圖1(a)為NOx數值范圍統計，以此確定常規運行區間為150～535 mg/m3，并通過上下限過濾掉超限的數據。圖1(b)標記了數值完全不變的停滯點數據。

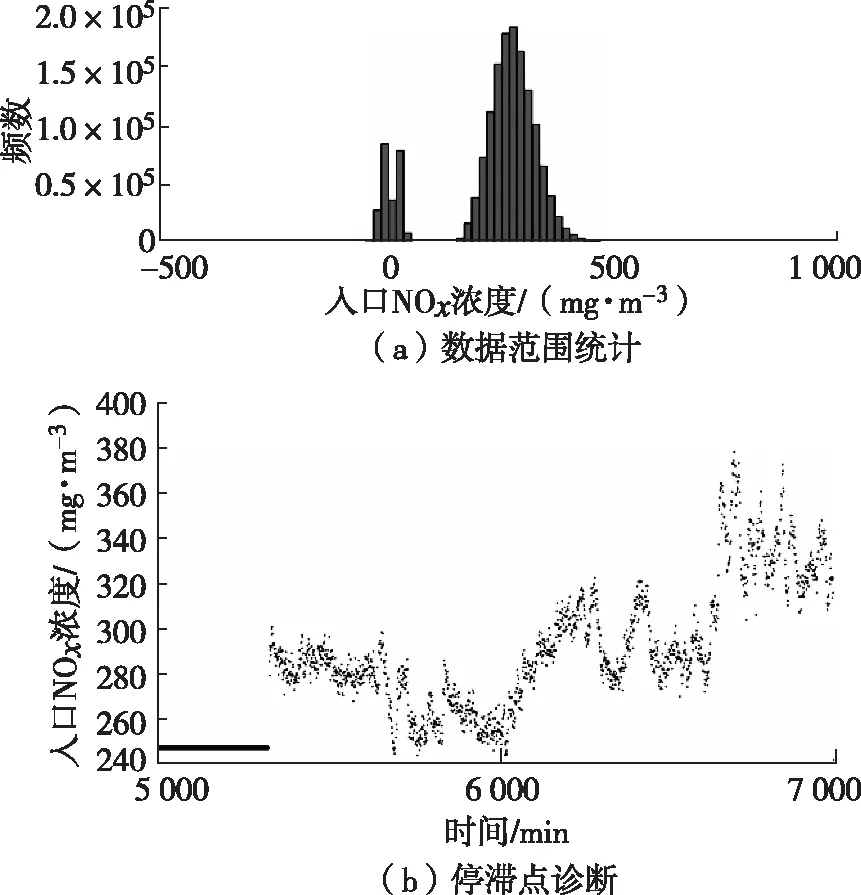
圖1 入口NOx濃度異常值診斷

2.2 非穩態點剔除

由于流動延遲及催化劑吸附反應固有的蓄氨機制，SCR過程常處于非穩態狀態，而本文是利用靜態關系模型將不同時間的脫硝效率修正到同一煙氣環境水平，再以此建立催化劑的性能劣化模型。因此，需要通過算法獲取穩態樣本。

2.2.1 基于t檢驗的穩態判定

第一種穩態檢驗算法是基于滑動窗對數據進行t檢驗[17]。算法可描述為：

xt=mt+μ+at

(1)

式(1)中，xt是時間窗內n個等距采樣的數據點；m為斜率，其估計值為時間窗內所有xt-xt-1的算數平均值；t為時間，min；mt為偏移分量；at是白噪聲序列；μ是平穩過程假設下的數據平均值，其估計值為：

(2)

式(2)中，n為時間窗內數據的個數。

由m和μ可計算白噪聲的標準差σa：

(3)

如果過程數據與其平均值之間的差值小于等于白噪聲標準差乘以其統計臨界值，可認為這個瞬間的數據點是穩定的，如果大于則不穩定的。

(4)

式(4)中，tcrit為白噪聲的統計臨界值，yt為t時刻xt數據的穩定性指標。

一個時間窗內數據的穩態值為式(4)中所有yt的平均值。當穩態值大于等于穩態閾值，這個數據點處于穩定狀態，穩態因子為1，反之為0。因此，算法中滑動窗口的大小和穩態閾值會影響穩態數據的判定。如圖2所示，本文選取一天的負荷數據，分別計算滑動窗口尺寸為10～50對應的穩態識別率(機器正確識別為穩態數據的數目與真實穩態數據數目之比)，得到滑動窗口為10時的穩態識別率最高，因此本文窗口大小選擇為10。針對同一段原始數據，分別選取穩態閾值為0.75～0.95，得到當穩態閾值取為0.75和0.8時，穩態識別率最高，如圖2(b)所示，但考慮到穩態閾值為0.75時的誤診率(機器錯誤識別為穩態數據的數目與機器識別為穩態數據的數目之比)較大，因此穩態閾值選擇為0.8。

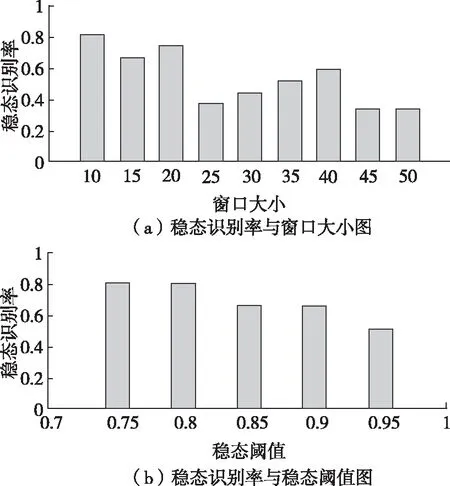
圖2 窗口大小和穩態閾值對識別率的影響

2.2.2 第一種基于R檢驗的穩態判定

第二和第三種穩態檢驗算法均是基于R檢驗法。為了減少計算負擔，第一種R檢驗法[18]采用過濾值估計數據的平均值Xf,i：

Xf,i=λ1Xi+(1-λ1)Xf,i-1

(5)

式(5)中，Xi是i時刻的數據值，λ為濾波系數，Xf,i是經一階濾波后，當前時間序列的濾波值。

第一種計算方差的方法是基于數據和平均值之間的差值加權：

(6)

(7)

(8)

2.2.3 第二種基于R檢驗的穩態判定

數據平均值為：

(9)

式(9)中，Xi是i時刻的數據值，N為數據個數。

第一種方差估計值為：

(10)

第二種方差估計值為：

(11)

將兩種方差之比作為R值：

(12)

對于兩種R檢驗法，R值越小，數據越可能趨近穩定狀態。將R值小于穩態閾值時，穩態因子為1，數據狀態為穩定，否則穩態因子為0。同樣對兩種R檢驗法選擇合適的窗口大小和穩態閾值。

2.3 三種穩態診斷算法測試

以1 d的負荷數據作為測試集，對比三種穩態算法的效果，三種穩態算法結果對比如圖3所示。對比可知，對于本對象數據集，基于t檢驗的穩態算法效果最好，能較準確識別出三段數據明顯為穩態的區域及一段數據波動但為穩態的區域。第一種R檢驗法會對部分穩態與非穩態過渡區的數據產生一定誤診，第二種R檢驗法對數據中的小波動非常敏感，會漏診較多穩態樣本。因此，本文采用t檢驗法提取原始數據中的穩態樣本。

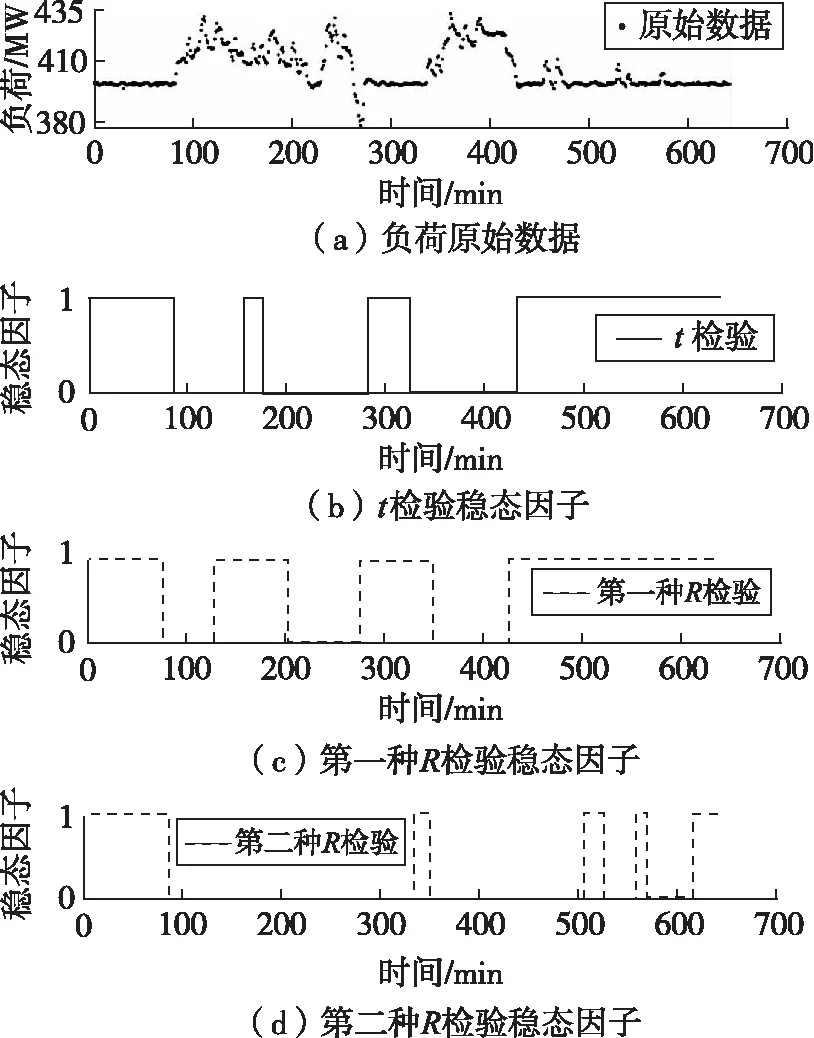
圖3 三種穩態算法結果對比

3 壽命預測

3.1 預測思路

對于結構確定的SCR脫硝系統，脫硝效率由兩方面因素決定，一個是煙氣環境，如空速、溫度和氨氮摩爾比等，而這些又由運行參數決定，如負荷和O2量會影響煙氣量的大小，從而影響空速；另一方面，脫硝效率還受催化劑自身活性決定，活性越高，脫硝效率越高。火電機組發電負荷受電網調度控制，會不斷變化，因此鍋爐內的煙氣環境也是不斷變化。本文的思路是將不同時期的脫硝效率修正到同一煙氣環境水平，此時脫硝效率只受活性影響，其變化趨勢可表征活性的變化趨勢。據此，利用修正后的效率數據分別訓練機理模型和數據驅動模型，并利用兩個模型預測未來催化劑活性劣化的趨勢，結果與真實穩態運行樣本比對。

3.2 脫硝效率的修正

對于SCR系統，可認為負荷、O2量、煙溫、入口NOx濃度和總尿素量5個參數可決定催化劑所處的煙氣環境。本文以大數據過濾器得到的穩態數據為樣本，分別以10 d、20 d、30 d為時間步長，將3年的歷史運行數據依次分成若干個樣本子集。對于每個步長所形成的樣本子集，時間跨度較短，如10 d可近似認為催化劑活性無變化，采用BP神經網絡建立脫硝效率與5個煙氣參數的靜態關系模型。BP神經網絡的拓撲結構為5-11-1，學習迭代次數為1 000，網絡學習精度為0.01。三種時間步長模型集最大、最小和平均誤差如圖4所示。由圖可知，時間間隔為10 d的時候，模型誤差最小。

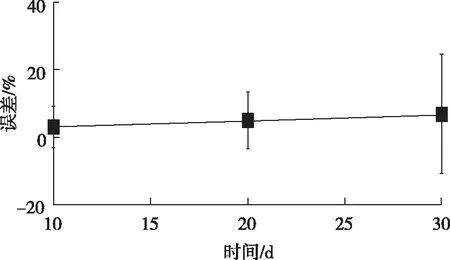
圖4 三種時間步長模型集最大、最小和平均誤差

選取3年中樣本最充足的工況作為修正工況：負荷為494 MW、入口NOx濃度為280 mg/m3、總尿素量為230 L/h、入口煙溫為323 ℃、氧量為3.1%。將該數據帶入10 d、20 d、30 d三個時間步長下的所有模型中，得到各個時間間隔脫硝效率隨時間的變化如圖5所示。由圖可知，三個步長下，脫硝效率的變化趨勢基本相同，證明該步長已足夠小，能保證單個步長內活性變化不大的假設成立。考慮到以10 d為周期，所建BP神經網絡精度較高，且供后續模型回歸的點數較多，因此本文以10 d為步長。

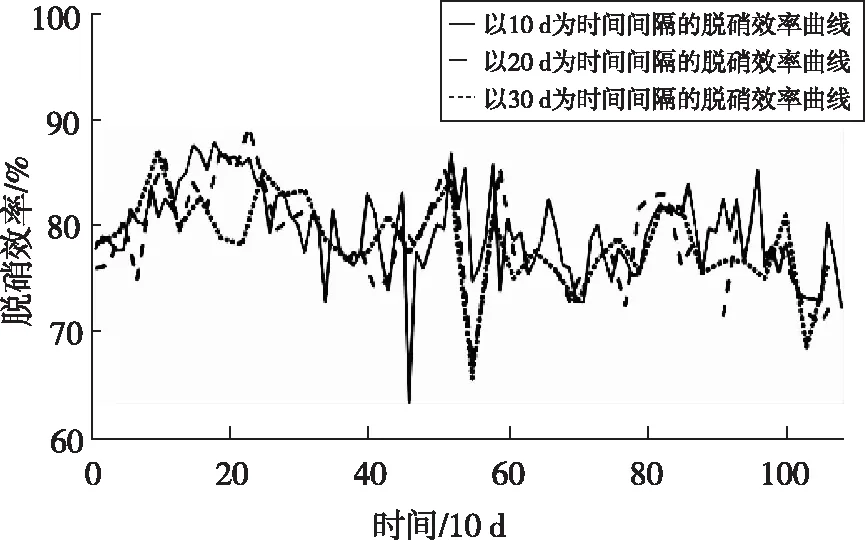
圖5 各個時間間隔脫硝效率的變化圖

3.3 機理模型框架

催化劑活性的定義為[15]：

(13)

式(13)中，Av為面速度(m/h)；MR為氨氮摩爾比；η為脫硝效率(%)。

若催化劑中毒、堵塞、磨損獨立造成催化劑失活，則失活模型為[15]：

(14)

式(14)中，Ki為毒性物質i的中毒失活速率系數，%/mol；Ci為毒物沉積速率，mol/h；V為SCR催化劑中V2O5總的物質的量，mol；t為SCR系統的運行時間，h；r為覆蓋率，即單位質量堵塞物質所覆蓋的面積，m2/kg；A為沉積速率，kg/h；S1為催化劑的比表面積，m2/kg；m為安裝催化劑的總質量，kg；G為煙氣流量，m3/h；c為磨損系數，即在平均飛灰粒徑下單位流量單位流速煙氣造成的磨損量，kg/(m5·h-2)；v為煙氣流速，m/h。

聯立公式(13)和公式(14)，求解脫硝效率為：

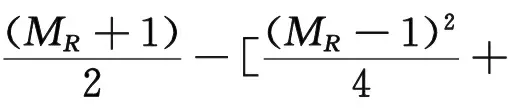
(15)

式(15)中與時間無關的參數提取為常數，并將時間單位統一為10 d，進一步得到：

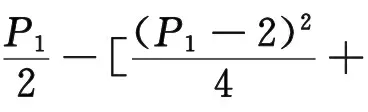
(16)

P1、P2、P3、P4、P5為模型的待定系數，表達式如式(17)所示。機理模型的訓練就是利用修正脫硝效率隨時間變化的數據訓練P1～P5。

P1=MR+1

(17)

3.4 數據驅動模型

采用時序預測模型ARIMA作為數據驅動模型的代表，利用修正后脫硝效率的數據進行回歸。對樣本集進行一階差分和二階差分，發現差別不大，這是由于活性隨著時間緩慢變化，因此將ARIMA模型中的d設置為1。圖6和圖7分別給出了自相關和偏自相關系數的序列圖，根據截尾的狀態，確定p與q分別取為2和3。

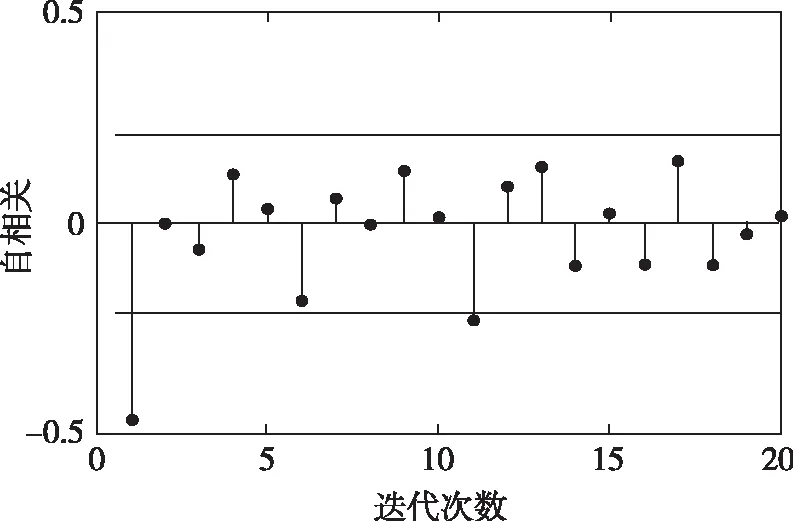
圖6 自相關系數的序列圖

圖7 偏自相關系數的序列圖

3.5 模型對比

采用10 d為步長，將3年數據分為108份，利用前90份的樣本子集，建立90個BP神經網絡，得到90個修正后脫硝效率點，以此訓練的機理模型與ARIMA(2,1,3)模型。采用第90～108組的數據驗證兩個模型預測未來脫硝效率的劣化趨勢，ARIMA模型與機理模型預測值對比如圖8所示。ARIMA模型預測值的平均相對誤差為4.31%，機理模型為7.42%。機理模型誤差相對較高，可能的原因是機理模型假設條件較多，諸如煙氣分布、飛灰顆粒粒徑及濃度分布、飛灰的沉積效應、煙氣中堿金屬、堿土金屬、硫的含量、低溫環境等因素及其變化對失活的影響無法充分考慮，因此對模型精度可能會有一定影響。

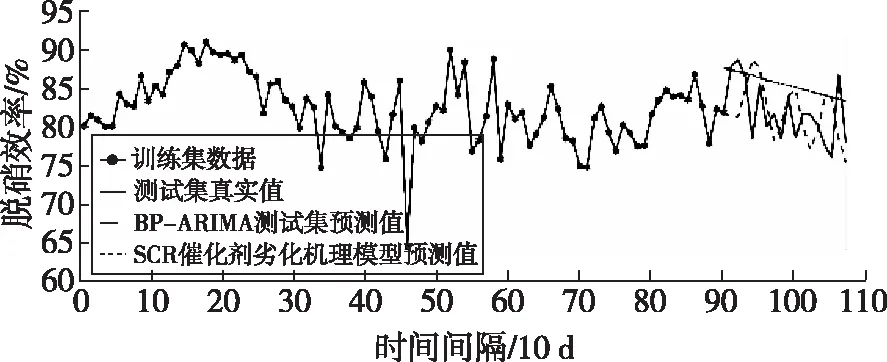
圖8 ARIMA模型與機理模型預測值對比

4 結語

本文以某660 MW電站鍋爐單側SCR反應器3年歷史數據為樣本，結合停滯點診斷、超限點診斷及對比三種穩態點診斷算法，得到大數據過濾器及高質量穩態樣本。據此，通過BP神經網絡將不同時期的脫硝效率修正到同樣煙氣水平，以表征催化劑活性的變化，并對比了機理驅動和數據驅動催化劑壽命劣化模型的準確性。主要結論為：

(1)相較于R檢驗法會對部分穩態與非穩態過渡區數據產生誤診及對數據中的小波動敏感，t檢驗法的穩態診斷效果較好；

(2)以10 d為步長建立脫硝效率修正模型的效率和精度均較高，且得到的劣化趨勢與20 d、30 d模型一致性較好，證明該步長能保證單個步長內活性變化不大；

(3)相較于機理模型框架，ARIMA模型預測精度更高，原因可能是由于電站SCR系統大尺度空間的分布特性及催化劑詳細失活機制無法全面考慮。